තවත් සාම්යන්...
ඉහත
පොදු සාම්යන් හැරුණු විට,
ප්රධාන
වශයෙන් අවකලන සාම්යයන්
ආශ්රයෙන් සාදාගත් පහත සඳහන්
සූත්රද අනුකලන සාම්යන් ලෙස
යොදා ගත හැකියි.
5.
∫
ex
dx = ex
+ c
මතකද
ex ශ්රිතය
අවකලනය කරන විට,
නැවතත්
ex ම
ලැබෙන බව පැවසුවා (අවකලනය
පාඩම්වලදී)?
එසේ නම්,
එහි විලෝම
වශයෙන්ද ex
අනුකලනය
කරන විට,
ලැබිය
යුත්තේ ex
ම තමයි
(ඊට
අමතරව c නම්
නියත පදයක්ද දැමිය යුතු බව
ඔබ දන්නවා).
6.
∫
1/x dx = ln(x) + c
මෙය
ගොඩනඟා ඇත්තේ d
ln(x)/dx = 1/x යන
අවකලන සාම්යය ආශ්රයෙන් බව
පේනවා නේද?
එනම්,
d
ln(x)/dx = 1/x
∫ [d
ln(x)/dx] dx = ∫
[1/x] dx දෙපැත්තම
අනුකලනය කිරීමෙන්
ln(x)
= ∫
1/x dx → ∫
1/x dx = ln(x)
අවකලනය
හා අනුකලනය එකට යෙදෙන විට ඒ
දෙක එකිනෙකට විලෝම නිසා දෙක
එකිනෙකට උදාසීන වී ගොස් ශ්රිතය
පමණක් ශේෂ වේ.
උදාහරණයක්
ලෙස, යම්
සංඛ්යාවක් 5න්
වැඩි කර,
නැවත 5න්
බෙදූ විට මුල් සංඛ්යාව වෙනස්
වන්නේ නැහැනෙ.
එලෙසම
යම් ශ්රිතයකට අවකලනය (හෝ
අනුකලනය)
යොදා
ඉන්පසුව අනුකලනය (හෝ
අවකලනය)
යොදන විට
ශ්රිතය නොවෙනස්ව පවතී.
6 වැනි සාම්යය ඇසුරින්ම මෙම සාම්යයත් ගොඩනැඟේ. මින් කියන්නේ යම් ශ්රිතයක් භාගයක හරය ලෙසද, එම ශ්රිතයේ අවකලනය එම භාගයේ ලවය වශයෙන්ද පවතින විට, භාගයක් ස්වරූපයෙන් තිබෙන එම සංයුක්ත ශ්රිතයේ අනුකලනය කළ විට, එම ශ්රිතයේ e පාදයේ ලඝු විය යුතු බවයි.
ln|f(x)|
ලෙස
ලියා තිබීමෙන් හැඟවෙන්නේ
f(x) ශ්රිතයේ
අගය ධන වුවත් ඍණ වුවත්,
ලඝු
බලන විට ධන අගයක් ලෙස පමණක්
තිබිය යුතු බවයි.
ඊට
හේතුව ඍණ සංඛ්යාවක ලඝු ගණනය
කිරීමට බැරි වීමයි.
යම්
සංඛ්යාවක් හෝ ගණිත ප්රකාශයක්
|| යන
සංඛේතයේ මැදට යොදන විට,
ඉන්
කියන්නේ එම සංඛ්යාව හෝ ප්රකාශය
ධන වුවත් ඍණ වුවත් හැමවිටම
ධන ලෙස සලකන්න කියාය (||
යන්න
නිරපේක්ෂ අගය සොයන ගණිත කර්මයේ
සංඛේතයයි).
මෙම
සූත්රයද අවකලන සූත්රයක
විලෝමය සලකා සාදා ගත් එකකි.
ඒ
කෙසේදැයි බලමු.
d ln(x)/dx = 1/x වන
බව ඔබ දන්නවා.
මෙහි
x වෙනුවට
f(x) ආදේශ
කළ විට,
එය
ශ්රිතයක ශ්රිතයක් බවට පත්
වේ. එවිට  යන දාම රීතිය යොදාගෙන පහත
ආකාරයට එය අවකලනය කළ හැකියි
නේද?
යන දාම රීතිය යොදාගෙන පහත
ආකාරයට එය අවකලනය කළ හැකියි
නේද?
ඉහත අවකලනයේ ප්රතිලෝමය දැන් සැලකූ විට ලැබෙන්නේ අපට අවශ්ය අනුකලන සාම්යයි. එනම්,
උදාහරණ කිහිපයක් බලමු.
ඉහත
ශ්රිතයේ හරය x2
වන අතර
එහි අවකලනය වන 2x
ලවයේ ඇත.
එනිසා
පහසුවෙන්ම මෙම සාම්යය යෙදිය
හැකියි.
8.
∫ ax dx =
ax/ln(a) + c
9.
∫ ln(x) dx = x.ln(x) –
x + c
10.
∫ sin(x) dx = - cos(x) +
c
11.
∫ cos(x) dx = sin(x) + c
12.
∫ tan(x) dx = -
ln|cos(x)| + c
13.
∫ cot(x) dx = ln|sin(x)|
+ c
14.
∫ sec(x) dx = ln |sec(x)
+ tan(x)| + c
15.
∫ csc(x) dx = - ln
|csc(x) + cot(x)| + c
16.
∫ sec2(x) dx =
tan(x) + c
17.
∫ csc2(x) dx =
- cot(x) + c
18.
∫ sec(x).tan(x) dx =
sec(x) + c
19.
∫ csc(x).cot(x) dx = -
csc(x) + c
ඇත්තටම
අනුකලනය අවකලනය තරම් පහසුවෙන්
සුලු කළ නොහැකියි.
අවකලනය
කිරීමට පහසුයි නම් අනුකලනය
අපහසු වන්නේ කෙසේදැයි ඔබට
සිතෙනු ඇත.
සංඛ්යාවක්
තවත් සංඛ්යාවකින් ගුණ කිරීම
හා එහි විලෝමය වන සංඛ්යාවක්
තවත් සංඛ්යාවකින් බෙදීම යන
ගණිත කර්ම දෙක සලකන්න.
වඩා පහසු
ගුණ කිරීම නේද?
ගුණ
කිරීමෙහි විලෝමය වන බෙදීම
එතරම් පහසුවෙන් සිදු කළ
නොහැකියිනෙ.
අන්න ඒ
වගේ තමයි අවකලනයට වඩා සුලු
කිරීම අමාරුයි අනුකලනයේදී.
එනිසා,
අනුකලනයන්
සුලු කිරීමේදී අනුකල සාම්යන්
ඉතාම ප්රයෝජනවත්ය.
විශාල
ප්රමාණයක් අනුකල සාම්යන්
ගොඩනඟා ගෙන ඇත (මා
ඉහත දැක්වූයේ ඉන් කිහිපයක්
පමණි).
කිසිවෙකුට
ඒසා විශාල අනුකල සාම්යන්
ප්රමාණයක් මතකේ තබා ගැනීමටද
බැරිය. එනිසා
ඔබට සියලු අනුකල සාම්යන්
මතක තබා ගැනීමට අවශ්ය නැත.
ඉහත පෙන්වා
දුන් ඒවා මතක තබා ගන්න.
තවද,
ඉහත
සාම්යන්ගෙන් බොහෝමයක් ඍජුවම
අවකලනය ආශ්රයෙනුයි ගොඩනඟා
ගෙන තිබෙන්නේ.
උදාහරණයක්
ලෙස, ටෑන්
අවකලනය කල විට සෙක්2
ලැබේ.
එවිට එහි
විලෝමය වන සෙක්2
අනුකලනය
කළ විට ටෑන් ලැබේ යැයි පැවසිය
හැකියිනෙ.
ඉහත 16
සිට 19
දක්වා
ඇති සාම්යන් 4ම
එලෙස ලබා ගත් ඒවාය.
අනුකලනයේදී
සෑම සාම්යක්ම ඉතාම වැදගත්ය.
ප්රමූලධර්මවලින්
අනුකලනය සෙවිය නොහැකිය.
එනිසා
සාම්යන් ආශ්රයෙන්ම ඒවා
විසඳීමට ඇති නිසා,
ලබා ගත
හැකි සෑම ලොකු කුඩා සාම්යක්ම
ගණිතඥයින් අත් හරින්නේ නැත.
මීට අමතරව
අනුකලනය සෙවීම සඳහා සුවිශේෂි
උපක්රම කිහිපයක්ද ඇත.



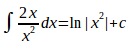

Comments
Post a Comment
Thanks for the comment made on blog.tekcroach.top