අවකලනය (differentiation) - 6

දෛශික අවකලනය

ඇත්තටම අවකලනයට දෛශිකද අදිශද යන්න එතරම් වැදගත් නැත. එහෙත් දෛශික රාශි සහිත ශ්‍රිතවල තිබෙන්නේ දෛශික නිසාත්, දෛශිකවලට සුවිශේෂි ගුණ පවතින නිසාත්, දෛශිකයන් අවකලනය කරන විට සැලකිලිමත් විය යුතු දේවල්ද තිබෙනවා. එනිසා දෛශික අවකලනය (vector differentiation) ගැන තරමක් විමසා බලමු.

මතකයට

දෛශික, අදිශ, හා ශ්‍රිත

දෛශික (vector) යනු දළ වශයෙන් අගයක් (value) හෙවත් ප්‍රමාණයක් (quantity) හෙවත් විශාලත්වයක් (magnitude) සහිත හා එම අගය/විශාලත්වය යොමු වී ඇති දිශාවක් (direction) සහිත භෞතික රාශින් වේ.

අදිශ (scalar) යනු දිශාවක් ගැන සැලකිලිමත් නොවී අගය ගැන පමණක් සැලකිලිමත් වන භෞතික රාශින් වේ.

උදාහරණ ලෙස, ඔබේ වයස අදිශ රාශියකි. උතුරු දිශාවට ඔබේ වයස 16යි; එහෙත් නැගෙනහිර දිශාවට ඔබේ වයස 70 යැයි පවසන්නේ නැහැනෙ. වයස, භාණ්ඩයක මිල, අඹ ගෙඩි ගණන ආදී කෙතෙකුත් දේවල් තියෙනවානෙ එලෙස අගයක් පමණක් සහිත රාශින්. එහෙත් මේ අතරේ තිබෙනවා අගයට අමතරව දිශාවද වැදගත් වන රාශින්. විශේෂයෙන් විද්‍යාත්මක හා තාක්ෂණ ලෝකයේ තමයි බහුලවම දෛශික රාශින් හමුවන්නේ. විදුලි ධාරාව, බලය, ප්‍රවේගය, ත්වරණය ආදිය ඊට නිදිසුන්ය.

දෛශික ගැන බොහෝ දේවල් විස්තරාත්මකව සාකච්ඡා කිරීමට ඇතත් මෙහි දැක්වෙන්නේ ඉතා කෙටි හැඳින්වීමක් පමණි. (දෛශික ගැනත් දෛශික අවකලනය ගැනත් වෙනමම ග්‍රන්ථයක් මා විසින්ම ලියා ඇත.)

දෛශික නිරූපණය

දෛශික රාශියක් නිරූපණය කළ හැකි ආකාර කිහිපයක් ඇත. අනිවාර්යෙන්ම අදිශ රාශියකින් දෛශික රාශියක් වෙන් කොට හඳුනාගැනීමට කුමක් හෝ දෙයක් කළ යුතුයිනෙ. සාමාන්‍යයෙන් දෛශික රාශිය තද අකුරින් (bold) පෙන්වනවා. උදාහරණ ලෙස:

5

x

AB

එහෙත් මෙය පරිගණක ආශ්‍රයෙන් ලියන අයට පහසුවෙන් කළ හැකි වුවත්, අතින් ලියන විට අකුරු තද කිරීම කරදරකාරී දෙයකි. එනිසා තවත් නිරූපණ ක්‍රමයක් භාවිතා කෙරෙනවා. එනම් දෛශික පදයට උඩින් කුඩා ඊහිසක් හෝ ඉරි කැබැල්ලක් යෙදිය හැකියි.

5

x

AB

තවද, යම් දෛශිකයක් නිරූපණය කිරීමට යොදා ගන්නා අකුරුවල දෛශික ස්වභාවය පෙන්වීමට සිදු කළ වෙනස්කම ඉවත් කළ විට නිකංම ඉංග්‍රිසි අකුරු හෝ සංඛේත පමණක් ඉතිරි වෙනවානෙ. මෙවිට ඒවා නිරූපණය කරන්නේ එම දෛශිකයේ විශාලත්වයයි (විශාලත්වය පමණක් සලකන නිසා එවිට ඒම අකුරු/සංඛේත අදිශ ලෙසද සලකන්න). උදාහරණයක් ලෙස උතුරු දිශාවට පවතින A නම් දෛශිකයේ වටිනාකම 4 යැයි සිතමු. එවිට, A = 4 වේ (දිශාව වැඩක් නැත මෙවිට).

ඉහත ක්‍රම දෙකම අදිශයකින් දෛශිකයක් වෙන් කොට හඳුනාගැනීමට ප්‍රමාණවත් වුවත්, ඒ දෙකෙහිම අගය පමණයි ඉන් අපට දැනගත හැක්කේ. දෛශිකයේ දිශාව ගැන හෝඩුවාවක් එම නිරූපණ ක්‍රම දෙකෙන්ම ලැබෙන්නේ නැත. එනිසා දෛශිකයක් දක්වන විට යම් ඛණ්ඩාංක තලයක් මත එය නිරූපණය කළ හැකි ආකාරයට දෛශික දක්වන්නට සම්මත කරගෙන ඇත. ඛණ්ඩාංක පද්ධතිද කිහිපයක් ඇති අතර, එම ඕනෑම පද්ධතියක් ඇසුරින් දෛශිකයක් නිරූපණය කළ හැකිය.

එහෙත් මා කාටිසියානු ඛණ්ඩාංක පද්ධතිය පමණක් යොදාගෙන දෛශික නිරූපණය කරනවා. යම් දෛශිකයක් මෙවිට ඛණඩාංක අක්ෂ ඔස්සේ විභේදනය කරලා දක්වනවා. මෙහිදී x අක්ෂය ඔස්සේ පවතින අගය වෙන්කොට හඳුනා ගැනීමට i අකුරක් එම අක්ෂය ඔස්සේ පවතින අගයට පිටුපසින් යොදනවා. ඒ ලෙසම, y අක්ෂය ඔස්සේ පවතින අගය පිටුපසින් j ද, z අක්ෂය ඔස්සේ ඇති අගයට පිටුපසින් k අකුරද යොදනවා.

 

ඒ අනුව පහත දැක්වෙන්නේ කාටිසියානු ඛණ්ඩාංක පද්ධතිය ආශ්‍රයෙන් නිරූපණය කර තිබෙන දෛශිකවලට උදාහරණ කිහිපයකි.

3i + 4j + 9k

-2i + 3j – 9k

9.3i + 34j

9z

උදාහරණයක් ලෙස පහත රූපයේ දැක්වෙන්නේ අක්ෂ 3ට විභේදනය කර තිබෙන දෛශිකයකි.

දෛශික ගණිත කර්ම

දෛශික රාශින් හා අදිශ රාශින් අතර විවිධ ගණිත කර්ම සිදු කළ හැකි අතර, ඒ සම්බන්ධ වැදගත් කරුණු කෙටියෙන් පහත දැක්වේ.

1. අදිශ රාශියක් තවත් අදිශ රාශියක් සමග එකතු හෝ අඩු කළ හැකියි (මෙය සාමාන්‍යයෙන් අප එදිනෙදා කරන එකතු හා අඩු කිරීමයි). දෛශික රාශියක් තවත් දෛශික රාශියක් සමග එකතු හෝ අඩු කළ හැකියි. දෛශික දෙකක් එකතු කිරීම දෛශික ආකලනය (vector addition) හා දෛශිකයක් තවත් දෛශිකයකින් අඩු කිරීම දෛශික ව්‍යාකලනය (vector difference) ලෙසත් හැඳින්වේ. ඇත්තටම දෛශික ව්‍යාකලනයද දෛශික ආකලනය තුළින්ම සිදු කරගත හැකියි (ඒ කියන්නේ සුලු කිරීම පැත්තෙන් බැලුවහම දෛශික ආකලනය හා ව්‍යාකලනය යන දෙකම එකයි). එනිසා දෛශික ආකලනය යැයි කී විට ඉබේම ඉන් දෛශික ව්‍යාකලනයත් ආවරණය වේ.

2. දෛශිකයක් අදිශයකින් ගුණ කළ හැකියි. මෙය "දෛශිකයක් අදිශයකින් ගුණ කිරීම" (vector multiplication by a scalar) ලෙස හැඳින්වේ. අදිශය හා දෛශිකය අතර ගුණ කිරීම දැක්වීමට සාමාන්‍යයෙන් x හෝ . යන සලකුණු යොදන්නේ නැත. s යනු යම් අදිශයක් නම් හා V යනු යම් දෛශිකයක් නම් මෙම ගුණිතය පහත ආකාරයට කෙටියෙන් ලිවිය හැකියි.

s(V) = sV

3. දෛශිකයක් තවත් දෛශිකයකින් ගුණ කිරීම. මෙම ගුණිතයේ ස්වරූප දෙකක් ඇත.

i. තිත් ගුණිතය (dot product) හෙවත් අදිශ ගුණිතය (scalar product) - මෙහිදී දෛශික 2 ගුණ වීමෙන් පසු ලැබෙන්නේ අදිශයකි (එනිසයි අදිශ ගුණිතය යන නම ලැබී තිබෙන්නේ). මෙම ගුණිතය නිරූපණය කිරීමට . යන සංඛේතය යොදා ගනී (එනිසයි තිත් ගුණිතය යන නම ලැබුණේ).

A . B = ABcos(θ)

ඉහත ගුණිතයෙන් කියන්නේ A හා B නම් දෛශික දෙක තිත් ගුණිතයෙන් ගුණ කරන විට, එම දෛශික දෙකෙහි විශාලත්වයන් දෙක එකිනෙකට ගුණ කර, එම දෛශික දෙක අතර තිබෙන කෝණයේ කොස් අගයෙන්ද ගුණ කරන්න කියාය.

cos(θ) පදය නිසා වැදගත් කරුණක් කියැවේ. එනම්, දෛශික දෙකම එකම දිශාවට නම් තිබෙන්නේ (ඒ කියන්නේ කෝණය 0 යි), කොස්(0)=1 නිසා, එම දෛශික දෙක තිත් ගුණිතයෙන් ගුණ කර ලැබෙන උපරිම අගය ඉන් ලැබේ. එහෙත් එම දෛශික 2 එකිනෙකට ලම්භකව නම් තිබෙන්නේ එවිට කොස්(90)=0 නිසා, එම දෛශික දෙකෙහි තිත් ගුණිතයද 0 වේ.

ii. කතිර ගුණිතය (cross product) හෙවත් දෛශික ගුණිතය (vector product) - දෛශික දෙකක් ගුණ කළ පසු නැවත ලැබෙන්නේද දෛශිකයකි (දෛශික ගුණිතය යන නම ලැබුණේ එලෙසයි). එම ගුණිතය හැඟවීමට x යොදා ගනී (එනිසයි කතිර ගුණිතය කියා කියන්නේ).

A x B = [ABsin(θ)]n

ඉහත නිරූපණයෙන් කියවෙන්නේ මෙයයි. A හා B දෛශික දෙකක් දෛශික ගුණිතයෙන් ගුණවන විට, ඒවායේ විශාලත්වයන් දෙක සාමාන්‍ය විදියට ගුණ කර, එම දෛශික දෙක අතර තිබෙන කෝණයේ සයින් අගයෙන්ද ගුණ කරන්න. එවිට එම අගයෙන් කියන්නේ ප්‍රතිපලය ලෙස ලැබුණු දෛශිකයේ විශාලත්වයයි. දෛශික 2 එකිනෙකට ලම්භක නම් හෙවත් කෝණය 90 නම්, සයින්(90) = 1 නිසා කතිර ගුණිතයේදී උපරිම අගය ලැබේ. එහෙත් ගුණ වන දෛශික දෙක සමාන්තර නම්, කෝණය 0 නිසා, සයින්(0) = 0 නිසා, කතිර ගුණිත ප්‍රතිපලය ශූන්‍ය වේ.

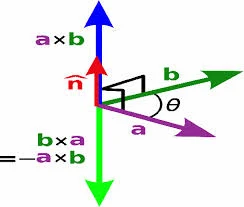
එහි දිශාව තමයි n යන අකුරින් කියන්නේ (ඒ අනුව n යන්නෙන් කිසිදු අගයක් ලැබෙන්නේ නැත; නිකංම දිශාව පමණයි ඉන් ගම්‍ය කරන්නේ). දෛශික දෙක කොලයක්/තලයක් මත ඉරි ආකාරයෙන් ඇන්ද විට එම තලයට ලම්භකවයි මෙම දිශාව පවතින්නේ.

ඉතිං, ඕනෑම තලයකට ලම්භකව පැවතිය හැකි දිශා දෙකක් පමණයිනෙ තිබෙන්නේ (තලයට උඩින් හා තලයට යටින්). දැන් මෙම දිශා දෙකෙන් කුමන දිශාවද දෛශිකයේ දිශාව විය යුත්තේ?

එය තෝරා ගන්නේ පහත රූපයේ දිස්වන ආකාරයටයි. කතිර ගුණිතයේ පළමුව ලියා ඇති දෛශික පදයේ (A) සිට දෙවැනියට ලියා ඇති දෛශික පදය (B) දක්වා පහත රූපයේ ආකාරයට අතේ ඇඟිලි කරකැවූ විට, එවිට මහපට ඇඟිල්ලෙන් පෙන්වන පැත්තයි/දිශාවයි තෝරා ගන්නේ.

 

දෛශික පද මාරු කළ විට, අගය වෙනස් නොවේ; එහෙත් දිශාව මාරු වේ. පහත රූපයේ එය නිරූපණය වේ. මෙම දිශාව මාරුවීම ධන ඍණ මාරුවීමක් ලෙසද සැලකිය හැකියි. එනිසා A x B = -(B x A) යන සම්බන්ධතාව පවතී.

 

දෛශිකයක් තවත් දෛශිකයකින් බෙදන්නට නොහැකිය. ඊට හේතුව එවැන්නක් තවමත් ගණිතඥයන් විසින් සම්මත කරගෙන නැති වීමයි (එසේ නොකරන්නට ඔවුනට හේතුද ඇත).

දැන් දෛශික හා අදිශ යන දෙවර්ගයේම රාශින්/විචල්‍යන් එක්ව සාදාගත හැකි ශ්‍රිත ගැන බලමු. දෛශික හා අදිශ යන දෙවර්ගයම එකතු වීමෙන් 4 ආකාරයක ශ්‍රිත සාදා ගත හැකියි. ස්වායත්ත විචල්‍යය හා පරායත්ත විචල්‍යය යන දෙකෙහි දෛශික අදිශ ස්වභාවය අනුවයි මෙම 4 වර්ගය සෑදී තිබෙන්නේ.

1. ස්වායත්ත විචල්‍යය අදිශයක් වන අතරම පරායත්ත විචල්‍යය අදිශයක් වීම. මෙතෙක් අප සලකා බැලුවේ මෙවැනි ශ්‍රිත තමයි. මේවාට දෛශික යන නාමය කිසිසේත් ගෑවෙන්නේ නැත. f(x)

උදාහරණ ලෙස, කාලයට සාපේක්ෂව දුර වෙනස්වීම (එනම්, වේගය) දක්වන ශ්‍රිතයක් සැලකිය හැකියි. කාලය හා දුර යන දෙකම අදිශයි.

2. ස්වායත්ත විචල්‍යය අදිශයක් වන අතරම පරායත්ත විචල්‍යය දෛශිකයක් වීම. අප මෙම කොටසේදී සලකා බලන්නේ මෙවැනි ශ්‍රිත ගැන පමණි. f(X) හෝ f(X)

උදාහරණ ලෙස, කාලයට සාපෙක්ෂව විස්ථාපනය වෙනස්වීම (එනම්, ප්‍රවේගය) දක්වන ශ්‍රිතයක් සැලකිය හැකියි. කාලය අදිශ වන අතර විස්ථාපනය දෛශික වේ.

3. ස්වායත්ත විචල්‍යය දෛශිකයක් වන අතරම පරායත්ත විචල්‍යය අදිශයක් වීම. F(x) හෝ F(x)

4. ස්වායත්ත විචල්‍යය දෛශිකයක් වන අතරම පරායත්ත විචල්‍යය දෛශිකයක් වීම. ඇත්තෙන්ම මෙම අවස්ථාව තරමක වෙනස්ම තත්වයකි (එහෙත් ඒ ගැන මෙහිදී අප විමසන්නට යන්නේ නැත). F(X) හෝ F(X)

යම් අදිශ ස්වායත්ත විචල්‍යයකට/රාශියකට සාපේක්ෂව විචලනය වන දෛශික පරායත්ත විචල්‍යයක/රාශියක ශ්‍රිත අවකලනය කරන අයුරු ගැන යම් තරමක් දුරට පමණයි මෙහිදී පෙන්වා දෙන්නේ (මේ ගැන පුලුල් විස්තරයක් දෛශික පොතේ ඇත).

දෛශික මත ගණිත කර්ම සිදු කරන විට පොදුවේ මතක තබා ගත යුතු කරුණ නම්, දෛශික පද ලියනු ලබන අනුපිළිවෙල වැදගත් බවයි. ගණිත කර්මය සිදු කරන විට වමේ සිට දකුණට දෛශික පද තිබෙන පිළිවෙලටම සලකන්නට වගබලා ගන්න.

F(t) යනු ස්වායත්ත විචල්‍යය (t) අදිශ හා පරායත්ත විචල්‍යය (F(t)) දෛශික ලෙස පවතින ශ්‍රිතයක් නම්, එය අවකලනය කිරීම යනු පහත ආකාරයේ ගණිත කර්මයකි.

බලන්න ඉහත සූත්‍රය සාමාන්‍ය අවකලනය කරන සූත්‍රයමයි. එකම වෙනස ශ්‍රිතය දෛශික වීමයි. ගණනය කිරීමේ වෙනසක් නැත. දෛශික ශ්‍රිතයක් අවකලනය කළ පසු ලැබෙන ව්‍යුත්පන්නය දෛශික ව්‍යුත්පන්නය (vector derivative) ලෙස හැඳින්වෙන අතර, එය පුරුදු නිරූපණ රටාවටම ලියන්න. එනම්,

dF(t)/dt = F'(t)

දෛශික අවකලන සාම්‍යයන්

සාමාන්‍ය අවකලන සාම්‍යයන්ට මේවා බොහෝ සේ අනුගතය. එහෙත් දෛශිකවල අමුතු ගුණ මතුවන තැන්හිදී සැලකිය යුතු කරුණු තිබෙන බැවින් ප්‍රධාන සාම්‍යයක් ගැන සොයා බලමු. F(t) හා G(t) යනු දෛශික ශ්‍රිත දෙකක් ලෙස හා s(t) යනු සාමාන්‍ය හෙවත් අදිශ ශ්‍රිතයක් ලෙසද සලකමු. මෙම ශ්‍රිත තුනෙහිම ස්වායත්ත විචල්‍යය t ලෙස දක්වා තිබෙන අදිශයකි.

දෛශික ශ්‍රිතයක් අදිශ ශ්‍රිතයකින් ගුණ කිරීම අවකලනය කරන්නට යොදා ගන්නා සූත්‍රයයි මෙය. ඉහත සූත්‍රයේ ප්‍රතිපලය හොඳින් බලන්න. එම පද ඔබට ඕන ඕන විදියට/පිලිවෙලට තැබිය නොහැකියි. ඒ දක්වා තිබෙන පිළිවෙලටම තැබිය යුතුයි (දෛශික සමග ගණනය කිරීම් කරන විට අනුපිලිවෙල ඔහේ වෙනස් කරන්නට බැහැ කියා මා මුලිනුත් ප්‍රකාශ කළා). උදාහරණයක් ලෙස ඉහත සූත්‍රයේ = ට වම් පැත්තේ පළමුව දක්වා තිබෙන්නේ දෛශිකය හා දෙවනුව අදිශයයි. එනිසා = ට දකුණු පැත්තේද හැමවිටම පළමුව දෛශිකය හා දෙවනුව අදිශය ලෙසයි අනුපිළිවෙල තැබිය යුත්තේ. ඉහත ගුණිතයේ පළමුව අදිශය හා දෙවනුව දෛශිකය තිබුණා නම් එම සූත්‍රය පහත ආකාරයට විය යුතුයි නේද?

 

 

ඇත්තටම දෛශික අවකලනය ගැන හොඳ අවබෝධයක් ලබා ගැනීමට දෛශික ගැන ගැඹුරු අවබෝධයක් අවශ්‍ය කෙරේ. මෙම පාඩම්වලින් දෛශික ගැන එවැනි දැනුමක් ලබා නොදෙන බැවින් ඩෙල්, ඩයිවර්ජන්ස්, කර්ල් වැනි ඉතා ලස්සන (හා ගැඹුරු) දෛශික අවකලන ක්‍රමවේද ගැන තවදුරටත් මෙහි සාකච්ඡා නොකෙරේ. දෛශික අවකලනය ගැන දළ අදහසක් පමණයි මින් ලබා දුන්නේ.