විශේෂ ශ්රිත කිහිපයක අවකලනය
1. dxn/dx
= nxn-1
මෙය
මුලින් දැක්වූ සාම්යයන්
ලැයිස්තුවේද පැවතියා.
ඒ ගැන තව
දුරටත් සාකච්ඡා කිරීමට අවශ්යයි.
බොහොමයක්
ශ්රිතවල විචල්යයන් යම්
බලයකට නංවා ඇති ආකාරයෙනුයි
හමුවෙන්නේ. ඉතිං
එවැනි දර්ශක සහිත හෙවත් බලයකට
නැංවූ පදයක් අවකලනය (differentiation) කිරීමට
දැනගත යුතුමයි. මෙම
සූත්රයෙන්/සාම්යයෙන්
ඉතාම පහසුවෙන් එකවරම අවකලනය
සිදු කළ හැකියිනෙ.
පදයේ
දර්ශකය විවිධාකාර විය හැකියි.
3, 7 වැනි ධන
පූර්ණ සංඛ්යාවක් විය හැකියි
(x3, x7); -2, -5 වැනි
ඍණ පූර්ණ සංඛයාවක් විය හැකියි
(x-2, x-5); 1/2, -3/5 වැනි
ධන හෝ ඍණ භාග සංඛ්යාවක් විය
හැකියි (y1/2, z-3/5).
මේ ආදී ලෙස
ඇති ඕනෑම අවස්ථාවක් සඳහා මෙම
අවකලන සූත්රය යෙදිය හැකි බව
සිහිතබා ගන්න.
මතකයට
යම්
පදයක දර්ශකය ඍණ නම්, එම
දර්ශකය ධන බවට පත් කර ගත හැකියි
පදය 1 ට
යටින් දැමීමෙන්. මෙය
දර්ශක රීතියක් බව ඔබට මතක ඇති.
x-3 =
1/x3 (y-1/2) = (1/y1/2)
යම්
සංඛ්යාවක් 1ට
යටින් දැමූ විට එය මුල් පදයේ
"ගුණිත
ප්රතිලෝමය"
(multiplicative inverse) ලෙස
හැඳින්වෙනවා. ප්රතිලෝම
වර්ග කිහිපයක් තිබෙන නිසා
ගුණිත ප්රතිලෝමය කියාම මෙය
හැඳින්වීම හොඳය. ඒ
අනුව x-3 හි
ගුණිත ප්රතිලෝමය 1/x3
වේ.
මෙම වචනය
මතක තබා ගන්න.
යම්
පදයක තිබෙන්නේ 1/2, 1/3 වැනි
භාග ස්වරූපයේ දර්ශකයක් නම්,
ඒවා "මූල"
(root) බවද මතක
තබා ගන්න. එනම්,
x1/2 යනු
x හි
වර්ග මූලයයි. X1/3 යනු
x හි
ඝන මූලයයි. Y1/7 යනු
y හි
හත්වැනි මූලයයි. මේ
අනුව සංඛ්යාවක මූලයන් ආකාර
දෙකකින් නිරූපණය කළ හැකියි
නේද?
X1/2 = √x
x1/3 =
3√x
x1/7 =
7√x
සංඛ්යාවක
මූල ගැන කතා කිරීමේදී සාමාන්යයෙන්
ඍණ මූල ගැන කතා කරන්නෙ නැහැනෙ.
එහෙත් දර්ශක
ගැන කතා කරන විට ඍණ දර්ශක ගැන
කතා කළ හැකියිනෙ. එමනිසා
x-1/2 වැනි
ප්රකාශයක් දර්ශක යොදා ගෙන
ලිව්වත් එය "මූලයක්"
ලෙස හඳුන්වන
සිරිතක් නැත (එලෙස
හඳුන්වනවා නම්, x හි
ඍණ වර්ගමූලය ලෙසයි හඳුන්වන්නට
සිදු වනනේ). එලෙසම
දර්ශකයේ ඇති භාග සංඛ්යාවේ
ලවය 1 නොවන
විටද සාමාන්යයෙන් මූල යන
වචනය යොදන්නේ නැත. එ්
අනුව x2/5 යන්න
x හි
2/5 වැනි
මූලය ලෙස කියන්නේ නැත.
එනිසා "මූල"
යන නම යොදන්නේ
සීමිත අවස්ථා ගණනකදී බවත්
දර්ශකවලට කිසිදු සීමාවක්
නැති බවද තේරුම්ගත යුතුය.
උදාහරණ
කිහිපයක් සලකා බලමු.
dX5/dx =
5x4
dy-3/dy =
-3y(-3-1) = -3y-4
d√x/dx
= dx1/2/dx = (1/2)x(1/2 – 1) = (1/2)x(-1/2)
= 1/2x1/2 = 1/2(√x)
dx2.4/dx
= 2.4x(2.4 -1) = 2.4x1.4
මෙම
සූත්රය පහත ආකාරයට සාධනය කළ
හැකියි. අවකලන
සූත්රයක් සාධනය කිරන්නේ
[f(x+∆x)
– f(x)]/∆x
සොයා
∆x
පදය
0 සීමාව
දක්වා ගෙන යෑමෙන්ය.
ඒ
අනුව,
f(x)
= xn
f(x+∆x)
= (x+∆x)n
f(x+∆x)
– f(x) = (x+∆x)n
– xn
(x+∆x)n
යන්න
ප්රසාරණය කළ විට පද n+1
සංඛ්යාවක්
ලැබේ. සාධනයට
අවශ්ය ප්රමාණයට මා පහත
දැක්වෙන සේ එය ප්රසාරණය
කරනවා. එහි
… ලෙස දක්වා තිබෙන කොටසෙහි
ඇති පද සියල්ලම ∆x
වලින්
ගුණ වී පවතී.
(x+∆x)n
= xn
+ nxn-1.∆x
+ … + (∆x)n
f(x+∆x)
– f(x) = xn
+ nxn-1.∆x
+ … + (∆x)n
– xn
= nxn-1.∆x
+ … + (∆x)n
[f(x+∆x)
– f(x)] / ∆x
= nxn-1
+ … + (∆x)n-1
දැන්
∆x
යන්න
0 සීමාව
කරා ගෙන යන්න.
එවිට
+ ... + තුළ
ඇති පද සියල්ලමත් (∆x)n-1
පදයත්
0 බවට
පත් වෙනවා (මොකද
එම කොටසේ ඇති සෑම පදයකම ∆x
වලින්
ගුණ වී තිබෙන නිසා;
උදාහරණ
ලෙස x.(∆x)
= x.(0) = 0 වේ).
එවිට
ඉතිරි වන්නේ nxn-1
යන්න
පමණි. එය
තමයි xn
වල
ව්යුත්පන්නය වන්නේ.
දැන්
සාධනය සම්පූර්ණයි.
2. dex/dx
= ex
මෙම
සම්බන්ධතාව අපූරුය. ඊට
හේතුව ex නම්
ශ්රිතය අවකලනය කළ විට නැවත
ලැබෙන්නේ එම ශ්රිතයමයි.
විචල්ය
පදය (x) තිබෙන්නේ
යම් නියතයක දර්ශකය ලෙසයි.
මෙවැනි
ශ්රිත ඝාතීය ශ්රිත (exponential
function) යැයි
පවසනවා. මෙම
අවස්ථාවේදී මෙම ඝාතීය ශ්රිතයේ
නියතය ලෙස ඇත්තේ e යන්නයි.
e වෙනුවට 10,
2, 101 ආදී ලෙස
වෙනත් නියත පදයක් වුවද පැවතිය
හැකියි ඝාතීය ශ්රිතයක.
e ආසන්න
වශයෙන් 2.7183 යන
අගයට සමාන වේ. 2, 103048, 2.7183
වැනි යම්
නිශ්චිත අගයකට නියතයක් හෙවත්
නියත පදයක් (constant)
යැයි කියනවා.
e යන්නට ඇත්තේද
නිශ්චිත අගයක් නිසා ඉබේම e
යන්නද නියතයක්
ලෙස හැඳින්වෙනවා. ගණිතයේ
තිබෙන සුප්රසිද්ධම නියත පද
දෙක තමයි e හා
π
කියන්නෙ.
e
වල වැදගත්කම
කුමක්ද, ඊට
2.7183 යන
අගය කෙසේ ලැබුණාද යන්න වෙනමම
කතා කළ හැකි හා කතා කළ යුතු
මාතෘකාවකි.
එය ගැන
සොයා බලන්න.
e සහිත
ඝාතීය ශ්රිතය සියලුම ඝාතීය
ශ්රිතයන්ගේ මූලික (“ඔරිජිනල්")
ස්වරූපය
ලෙස සැලකුවාට වරදක් නැත.
උදාහරණක්
බලමු. y
= e2x
යන ශ්රිතය
x විෂයෙන්
අවකලනය කරන්න.
මෙය ඇත්තටම
ශ්රිතයක ශ්රිතයකි.
2x=t ලෙස
සිතුවොත් එය පැහැදිලි වේවි.
එවිට et
යන්න
භාහිර ශ්රිතය ලෙසත් t=2x
යන්න
අභ්යන්තර ශ්රිතය ලෙසත්
පේනවා නේද?
දාම රීතිය
යොදා මෙය සුලු කළ හැකියි දැන්.
dy/dt
= det/dt
= et
= e2x
dt/dx
= d2x/dx = 2
(dy/dt).(dt/dx)
= e2x.2
= 2e2x
3.
dax/dx
= ax.ln(a)
ඉහත
2 හිදී
සලකා බැලුවේ ex
නම් මූලිකම
ඝාතීය ශ්රිතයේ අවකලනයයි.
දැන් සලකා
බලන්නේ ඕනෑම ඝාතීය ශ්රිතයක
අවකලනයයි (එනම්
a යන්න
ඕනෑම අගයක නියතයකි;
එය 10
විය හැකියි;
101 විය
හැකියි;
ඕනෑම
අගයක් විය හැකියි).
බලන්න
මෙහි ඇති රටාව.
අවකලනයට
භාජනය කළ ශ්රිතය නැවත ලැබේ.
එහෙත්
මෙහිදී අමතරව ln(a)
පදයකින්
එය ගුණ කළ යුතු වෙනවා.
ex
ශ්රිතයේ
අවකලනයට වඩා ඇති එකම වෙනස මෙම
ln(a) යන
කොටසයි.
ln(a)
යනු a
නම් නියත
පදයේ ලඝුගණකයයි.
තවද,
එම ලඝුගණකයේ
පාදය e වේ.
සාමාන්යයෙන්
ලඝු ලියන්නේ logපාදය
(ලඝුපාදය)
ලෙසනෙ.
උදාහරණ
ලෙස log10,
log2,
loge
දැක්විය
හැකියි. e
පාදයේ
ලඝුගණක ගන්නා විට එය loge
ලෙස නොලියා
ln ලෙස
කෙලින්ම ලිවිය හැකියි.
වෙනත්
විශේෂත්වයක් ln
වල නැත.
ln ක්රියාත්මක
වන්නේ a නම්
නියතය මත බැවින් පිළිතුර ලෙස
ලැබෙන්නේද නියතයක්මයි.
ඒ කියන්නේ
ln a යනු
නියත පදයකි.
අවශ්ය
නම් මෙම සූත්රයෙන්ම dex/dx
= ex
යන සූත්රයත්
පහසුවෙන්ම සාධනය කළ හැකියි.
dax/dx
= ax.lna
හි a
ට e
ආදේශ
කරන්න.
ඉන්පසු
සුලු කරන්න.
dax/dx
= ax.ln
a → dex/dx
= ex.ln
e = ex.1
= ex
ln(e)
= 1 වේ.
(යම්
සංඛ්යාවක එම සංඛ්යාවම පාදය
ලෙස ඇති ලඝුගණකය ගත් විට පිළිතුර
1 වේ;
log10
= 10 = 1 නේද?
එලෙසම
ln e = loge
e = 1 වේ.)
උදාහරණයක්
ලෙස y=2(4x)
යන ශ්රිතය
x විෂයෙන්
අවකලනය කරන්න.
dy/dx
= d2(4x)/dx
= 2d(4x)/dx
= 2(4x.ln(4))
= 2(4x)(1.3863)
= 2.7726(4x)
4.
d
ln(x) /dx = 1/x
මෙම
සූත්රය ඉතාම සරලයි.
යම් පදයක
e-පාදයේ
ලඝුගණකය අවකලනය කරන විට,
පිළිතුර
ලෙස ලැබෙන්නේ එම පදයේ ගුණිත
ප්රතිලෝමයයි (එනම්,
“එක යට
සංඛ්යාව").
උදාහරණයක්
බලමු. ln(x2)
හි අවකලනය
සොයන්න.
මෙයද
ශ්රිතයක ශ්රිතයකි.
පළමුව
අභ්යන්තර ශ්රිතයේ අවකලනය
(dx2/dx)
සොයමු.
එය 2x
වේ.
ඉන්පසු
භාහිර ශ්රිතයේ අවකලනය (y')
සොයමු.
එය 1/x2
වේ.
එවිට
අවසාන පිළිතුර වන්නේ (2x).(1/x2)
= 2x/x2
= 2/x වේ.
5
d
loga(x)/dx
= 1/(x.ln(a))
මෙය
ඉහත d ln(x)/dx =
1/x යන්නෙහිම
අනෙක් සූත්රයයි.
e පාදයේ
ලඝුගණකය බලන විට එම සූත්රය
යොදන අතර,
මෙම සූත්රය
යොදන්නේ වෙනත් ඕනෑම පාදයකින්
ගත් ලඝුගණකයක් අවකලනය කරන
විටයි.
බලන්න
ඕනෑම පාදයක ලඝුගණකය අවකලනය
කරන විට ලැබෙන පිළිතුරෙහි e
පාදයේ
ලඝුගණකය අවකලනය කරන විට ලැබෙන
පිළිතුරෙහි වෙනස.
රටාවක්
එතැන ඇත.
ඕනෑම
පාදයක ලඝු ඇති අවස්ථාවේදී
ln(a) නම්
නියත පදයෙන් හරය ගුණ කර ඇත.
ඇත්තටම
e පාදයේ
ලඝු අවකලනය කරන සූත්රය පවා
මෙම සූත්රයෙන් සාධනය කළ
හැකියි.
මෙම
සූත්රයෙහි a
යන්නට e
ආදේශ කර
සුලු කරන්නට විතරයි තිබෙන්නේ
එය සාධනය කිරීමට.
d
loga(x)/dx
= 1/(xln(a)) → d loge(x)/dx
= 1/(xln(e)) = 1/x(1) = 1/x
6.
ත්රිකෝණමිතික
(trigonometric) අනුපාතවල අවකලනයන්.
i.
d
sin(x)/dx = cos(x)
ii.
d
cos(x)/dx = -sin(x)
iii.
d
tan(x)/dx = sec2(x)
iv.
d
sec(x)/dx = sec(x).tan(x)
v.
d
csc(x)/dx = -csc(x).cot(x)
vi.
d
cot(x)/dx = -csc2(x)
උදාහරණ
කිහිපයක් බලමු.
පහත උදාහරණ
දෙකම ශ්රිතයක ශ්රිත වේ.
d
sin(2x3)/dx
= (6x2).(cos(2x3))
= 6x2cos(2x3)
d
tan(3y)/dy = (3).(sec2(3y))
= 3sec2(3y)
ඉහත
සූත්රවලින් කිහිපයක් සාධනය
කරමු. පළමුව
සයින් සූත්රය සාධනය කරමු.
f(x+∆x)
– f(x) = sin(x+∆x)
– sin(x)
=
sin(x)cos(∆x)
+ cos(x)sin(∆x)
– sin(x)
[f(x+∆x)
– f(x)]/∆x
= [sin(x)cos(∆x)
+ cos(x)sin(∆x)
– sin(x)]/∆x
දැන් අපි ටෑන් ශ්රිතයේ අවකලනය සිදු කරන අයුරු බලමු.
7. ත්රිකෝණමිතික (trigonometric) ප්රති-අනුපාතවල අවකලනයන්.
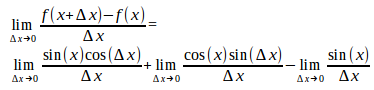







1. dxn/dx = nxn-1 pramuuladarma walin awakalanaya karala pennanna puluwanda. mata eeka tikak patalili sahagathayi. saadhanaye anthima piyawara 3 tikak wisthara karannaa.... mata ee tika theren na.
ReplyDeletehm... pramuladarma walin avakalanaya karana kota hama thissema liyana swarupaya thamai lim Δx->0 [f(x+Δx) - f(x)]/Δx yanna. ithin ema suthraya liya adesha kara sulu kirima kara balanna.
Deletelim Δx->0 [f(x+Δx) - f(x)]/Δx
lim Δx->0 [(x+Δx)^n - x^n]/Δx
=lim Δx->0 [x^n + ax^n-1(Δx) + bx^n-2 (Δx)^2 + cx^n-3 (Δx)^3 + ... + yx(Δx)^n-1 + z(Δx)^n - x^n]/Δx
(sangunaka pada man a,b,c,...,y,z lesa gena atha prakasaya ketiyen pahasuwen liweema sandaha)
=lim Δx->0 [ax^n-1(Δx) + bx^n-2 (Δx)^2 + cx^n-3 (Δx)^3 + ... + yx(Δx)^n-1 + z(Δx)^n]/Δx
=lim Δx->0 [ax^n-1 + bx^n-2 (Δx) + cx^n-3 (Δx)^2 + ... + yx(Δx)^n-2 + z(Δx)^n-1]
= ax^n-1 + bx^n-2 (0) + cx^n-3 (0)^2 + ... + yx(0)^n-2 + z(0)^n-1]
= ax^n-1
prakashaya dik wena nisa man sangunaka pada a,b,c,...y,z lesa gatthath ema sangunaka pada n asrayen pawasiya hakiy. pascal thrikonaya ho wenath kramayakin (sadarana bahupada prakasaya liyaa) e baw pahasuwenma penewi. e anuwa, a=n ve. ewita
ax^n-1 = nx^n-1
sthuthi :)
ReplyDeletemata pramuuladarma walin awakalanaya therenawaa. habayi ee saamya pramuuladarma walin oppu kiriima thamayi theeren naththee. man eeka awakalanaya kalee wena widihakata. ekata wada obe kramaya pahaasui. namuth mata theren naththe oba
lim Δx->0 [(x+Δx)^n - x^n]/Δx
=lim Δx->0 [x^n + ax^n-1(Δx) + bx^n-2 (Δx)^2 + cx^n-3 (Δx)^3 + ... + yx(Δx)^n-1 + z(Δx)^n - x^n]/Δx
kiyaa liiwee ayi kiyaa. ee piyawara pahadili karannakoo...
mn ee saamya sadanaya kirima igenagaththee
{man delta x wa Ax kiyala pennannam}
y=x^n ----(1)
Y+Ay= (x+Ax)^n -----(2)
(2)-(1)
dy/dx = lim [Ax->0 (x+Ax)^n-x^n]/Ax
= lim x+Ax->x [Ax->0 (x+Ax)^n-x^n]/(x+Ax)-x
siimaa prameeya anuwa ;
dy/dx = nx^n-1
kiyalayi man igenagaththee. mata ee sima prameya saadanaya karala pennanna puluwanda?
obata dan nam thiyenne avakalanaya gataluwak neme, sarala veeja ganitha gataluwak... (a+b)^2 = (a+b)x(a+b) = a^2 + 2ab + b^2 neda? e widiyatama (a+b)^3 = (a+b)x(a+b)x(a+b) = a^3 + 3a^2b + 3ab^2 + b^3 neda? elesema 4 vani balaya, 5 vani balaya aadi lesa "n" vani balaya uwath dakwiya hakiyne. ithin (x+Δx)^n yanu (a+b)^n vani prakasayak. eya prasaranaya kalaama x^n + ax^n-1(Δx) + bx^n-2 (Δx)^2 + cx^n-3 (Δx)^3 + ... + yx(Δx)^n-1 + z(Δx)^n labenawa. meda "..." lesa thith godak (ema thith goda english walin ellipsis kiya sinhalen ලුප්තය kiya hadinviya hakiy mata mathaka vidiyata)... in kiyanne thawath dewal (pada) thibena bawai. man hithanne oba ge gena dannawa. (a+b)^n akaaraye ganitha prakasa bahupada prakasha lesa hadin wenawa... e gena thawath tikak igena ganna :)
Deleteoba liya thibenneth man liyapu ekamai... oba liyapu kramen (2) - (1) kiyanne (x+Δx)^n - x^n yannamai. lim (x+Ax) -> x yannen adahas wenne Ax->0 yannama neda (Ax binduwa unama x+Ax = x wenawane)?
sthuthii...��
ReplyDeletemn ee gana soyaa baluwaa. oba a,b,...,z lesa handinwuu sangunaka pada monawaada? mn hithanne ewa n,n-1,n-2,...,1,0 wiya yuthuyi.
hikiz... mn adahas kalee eeka neweyii...x=0 nm itin x+y=y kiyaa nodanne kawda?..��
mn kiwwe mokakhari siima sambanda prameeyak thiyenawada kiyaa Lim y->0 y^n-x^n]/y-x = nx^n-1 kiyaa. mata eeka hambunaa obe pothaka thibii...�� eeka saadanaya karala pennanna puluwanda kiyalaa thamayi ,ama oben ahuweee...........
sangunaka pada obata kamathi nirupana kramayakin dakwiyak hakiy... ithin mama sarala kramayak wana, a,b,c aadi lesa english letters bawitha kala... ema sangunakama kamathi nam අ, ආ, ඇ aadi lesa sinhala akurin ho α,β,γ,θ aadi lesa greek akurin ho wenath onama sanketha kramayakin dakwiya hakiy... ewa hudu sanketha pamani... ithin oba kiyu lesa ema sangunaka pada n1, n2, n3 aadi lesa ho a1, a2, a3 (mehi 1, 2, 3 aadi ilakkam yatakuru (enam kudaa akuru) lesa samanyen thabenawa... eheth me comment box eke yatakuru dakwanna amarui) aadi lesa dakwiya hakiy.
Deleteoba mulinma ahapu prasne uda thiyenawane... ekata man uttharayak deela thiyenawa... dewaniyata deela thiyena uttharaya oba dewaniyata ahapu prasneta... oba dan ahana "Lim y->0 y^n-x^n]/y-x = nx^n-1 " yanna meeta kalin oba ahala na... mama ehema ekak kohewath liyalath na... obe comment uda thiyenawane... kiyawala balanna...
igena ganna kota tharka karamin igena ganna eka hondai... eheth thaman adahas kala de hariyata kiyannath purudu puhunu wenna... awankawa adahas prakasa karannath purudu wenna...
aa thawa deyak e kiyanne mokadda ? kohomada ee niyathaya hadaaganne ? ("pi" wa C/d walin hadagaththa wagee) log e padayata x wa ln x kiyaa handunwannee ai ? (ai eyata witharak special?)
ReplyDeleteme gena itha honda lipiyak wikipedia eke thiyenawa... https://en.wikipedia.org/wiki/E_(mathematical_constant)
Deleteema niyathayath ahamben soya gath ekak. (1+1/n)^n yana ganitha prakaasaye "n" padaye agaya ananthaya karaa yana wita ema prakasaye agaya abisaari wenawa (e kiyanne 2.8183...vani agayakata enna enna lan wenawa). ganitha ha widyawa thula swabawayenma mema niyatha padaya muna gahenawa... vidyawa kramayen igena ganna vita e e thanwaladi obatama eya muna gasewi... eha swabawayenma mathu wanawa (kawruth onakamin ema niyatha padaya yoda gannawama nemei). eeta hethuwa ema niyatha padayath swabawikawa pawathina darmathaawak (hariyata skandayak thiyenawa wita ethana newtonta anuwa guruthwakarasanayak ho einsteinta anuwa awakasa kaala vakrathawak thiyennaa se).
e niyathaya paadaya karagen lagu (log) sewiya hakiy (atthatama onama paadayakin lagu sewiya hakiyne; namuth bahuwlawama 10 paadaya, 2 paadaya, e paadaya thamai yoda ganne). ithin log_e(x) yanna nitharama bawitha wena nisa eya ketiyen ln(x) lesa liyannath sammatha kara gattha... ekata wisesa rupayak labee thiyenne eya etharam wedagath ho nithara bawitha wena nisai...