දෛශික (vectors) - 3

දෛශික බෙදීම

දෛශිකයක් තවත් දෛශිකයකින් බෙදිය නොහැකිය. එය අවලංගු අවස්ථාවකි. ගණිතයේ මෙබඳු අවලංගු අවස්ථා ගණනාවක් හමු වේ (ශූන්‍යය ශූන්‍යයෙන් බෙදීම, අනන්තය අනන්තයෙන් බෙදීම, ශූන්‍යයෙහි ශූන්‍ය වැනි බලය ආදිය).

යම් දෛශිකයක පරස්පරයද (ප්‍රතිලෝමය) නැත (එනිසා, a දෛශිකයක් 1/a ලෙස ලිවිය නොහැකිය). මෙනිසාම යම් අදිශයක් දෛශිකයකින් බෙදිය නොහැකිය මොකද දෛශිකයක් භාග සංඛ්‍යාවක හරය ලෙස නොපවතින නිසා (පරස්පරයක් ලෙස ලිවිය නොහැකි නිසා).

එසේ වුවත් දෛශිකයක් අදිශයකින් බෙදිය හැකිය. එහිදී අදිශයකින් බෙදීමක් ලෙස වෙනුවට දෛශිකයේ විශාලත්වය කුඩා කිරීමක් යන අර්ථයෙන් එය සැලකිය හැකිය (මේ ගැන දෛශික ගුණාකාර කොටසේදී අප සලකා බලා ඇත). උදාහරණයක් ලෙස, නිව්ටන් 20ක දෛශිකයක් 20/5 ලෙස 5න් බෙදා නිව්ටන් 4 ලෙස සුලු කළ හැකිය. තවද, 30i + 20j - 55k වැනි ආකාරයෙන් ලියා ඇති දෛශිකයක් වුවද යම් අදිශයකින් බෙදීම (30i + 20j - 55k)/5 වැනි ආකාරයට ලිවිය හැකිය. එවිට එහි එක් එක් සංරචකය වෙන වෙනම බෙදා අවශ්‍ය නම්, (30/5)i + (20/5)j - (55/5)k = 6i + 4j - 11k බවට සුලු කළ හැකියි.

දෛශික ගුණ කිරීම

දෛශික ගුණ කිරීම් වර්ග දෙකක් ඇත. ඇත්තෙන්ම දෛශික ගුණිත දෙකක් පවතින්නට හේතුව ගැන සිතා බලන විට විද්‍යාව හා ගණිතය අතර තිබෙන අන්‍යොන්‍ය සබඳතාව හොඳින් පෙනේ. ගණිතය තුල දෛශික හා ඊට සම්බන්ද ගණිත කර්ම ඉගෙන ගන්නේ විද්‍යාව තුල දෛශික ගුණ තිබෙන රාශින් හමුවන නිසාය (මෙලෙස අනුන් (විද්‍යාව) වෙනුවෙන් ගණිතය "කඩේ යයි" මොකද ගණිතය යනු විද්‍යාවේ භාෂාවයි). ඉතිං, මේ ලෝකය තුල දෛශික රාශින් දෙකක් එකිනෙකට ගුණ කරන විට, දෙයාකාරයකින් හැසිරෙන බව පෙනේ. උදාහරණයක් ලෙස, බලය හා එම බලය නිසා ඇති වන විස්ථාපනය යන දෛශික රාශි දෙක එකිනෙකට ගුණ කළ විට කාර්ය නම් අදිශ රාශියක් ලැබෙන අතර, බලය හා ඊට ලම්භක විස්ථාපනයක් යන දෛශික රාශි දෙක ගුණ කළ විට බල ඝූර්ණය නම් දෛශික රාශියක් ලැබේ. ලෝකයේ ස්වභාවය එබඳුය. එනිසා එම අවස්ථා දෙක වෙන වෙනම නියෝජනය කිරීමට දෛශික ගුණිත දෙකක අවශ්‍යතාව මතු වෙන බව අමුතුවෙන් කිව යුතු නොවේ.

අදිශ ගුණිතය

මෙහිදී දෛශික දෙකක් ගුණ වී ලැබෙන පිලිතුර අදිශ රාශියකි (එනම් දිශාව වැඩක් නැති විශාලත්වය පමණක් ඇති). එනිසා අදිශ ගුණිතය (scalar product) ලෙස හැඳින්වේ. අදිශ ගුණිතයේ වැඩි කිරීම සංඛේතවත් කරන්නේ තිතක් මඟිනි (වෙනත් සංඛේත භාවිතා කළ නොහැකිය). එනිසාම එය තිත් ගුණිතය (dot product) ලෙසද හැඳින්වේ.

a . b

අදිශ ගුණිතයේදී සිදු වෙන්නේ දෛශික දෙකෙහි විශාලත්වයන් දෙක සාමාන්‍ය පරිදි ගුණ කර, ඉන්පසුව එම ගුණිතය නැවත එම දෛශික දෙක අතර පවතින කෝණයේ කොස් අගයෙන් ගුණ කිරීමයි.

a . b = |a| |b| cosθ

සාම්ප්‍රදායිකව එය නිර්වචනය කරන ක්‍රමයක්ද ඇත. එය නම්, අදිශ ගුණිතයට හවුල් වන දෛශික දෙකෙන් එක් දෛශිකයක විශාලත්වය හා අනෙක් දෛශිකය විසින් පෙර දෛශිකය මත ඇති කරන ප්‍රක්ෂේපණයේ විශාලත්වයෙන් ගුණ කිරීම අදිශ ගුණිතයයි.

උදාහරණයක් ලෙස, යම් වස්තුවක් මත නිව්ටන් 100ක බලයක් ක්‍රියාත්මක කරමින් මීටර් 10ක දුරක් ගමන් කර වූයේ යැයි සිතමු. තවද, බලය හා විස්ථාපනය යන දෙකම එකම දිශාව ඔස්සේ පවතී යැයි සිතමු. ඒ කියන්නේ දෛශික දෙක අතර කෝණය අංශක 0කි. මෙවිට එම බලය හා ඉන් ඇතිවන විස්ථාපනය නිසා යම් කාර්යක් සිදු වී ඇතැයි කියති. මෙම කාර්ය ප්‍රමාණය ගණනය කරන්නේ අදිශ ගුණිතය මඟිනි. එය 100x10.cos0 = 1000x1 = 1000 කි. කාර්යක් නිසා එහි ඒකකය ජූල් වේ. විද්‍යාව ඉගෙන ගත් ඔබ දන්නවා කාර්ය හා ශක්තිය යන දෙකම අදිශ රාශි බවත් ඒ දෙකම ජූල් යන සම්මත ඒකකයෙන් ප්‍රකාශ කරන බවත්.

තවත් උදාහරණයක් බලමු. පහත රූපය බලන්න. සුමට මතුපිටක් මතින් යම් වස්තුවක් ඇඳගෙන යෑමක් එහි දැක්වේ (සුමට නිසා ඝර්ෂනයක් නැතැයි ගත යුතුය). එහි a දෛශිකයෙන් නිරූපණය කෙරෙන්නේ මිනිසා විසින් යොදන බලයයි. එය පොලොවට/තිරසට t කෝණයකින් වස්තුව මත යෙදේ. මෙම ඇඳගෙන යෑමේ බලය නිසා, පොලොව මතුපිටින් එම වස්තුව b යන දෛශිකයෙන් නිරූපණය කෙරෙන යම් විස්ථාපනයක් සිදු කරයි. එවිට, සිදු කරන කාර්ය රූපයේ දැක්වෙන ප්‍රකාශනයෙන් දැක්වේ (ඉහත උදාහරණයේදී දෛශික දෙක අතර කෝණයක් නැති අතර මෙම උදාහරණයේදී කෝණයක් තිබේ; එකම වෙනස එයයි මෙම උදාහරණ දෙකෙහි).

ඉහත සූත්‍රය අනුව පැහැදිලි වෙනවා දෛශික දෙකම එකම දිශාවට පවතී නම් (එනම් ඒ දෙක අතර කෝණය 0 යි), කොස් 0 = 1 නිසා, කෙලින්ම එම දෛශික දෙකෙහි සංඛ්‍යාත්මක අගයන් (එනම් දෛශික දෙකෙහි විශාලත්වයන්) දෙක එකිනෙකට ගුණ කිරීමට පමණයි තිබෙන්නේ. එලෙසම, දෛශික දෙක එකිනෙකට විරුද්ධ දිශා ඔස්සේ පවතී නම්, කොස්180 = -1 නිසා, කෙලින්ම එම දෛශික දෙකෙහි සංඛ්‍යාත්මක අගයන් එකිනෙකට ගුණ කර - සලකුණ සහිතව ලියන්න. එහෙත් අදිශ ගුණිතයේදී, ගුණ වන දෛශික දෙක එකිනෙකට ලම්භක නම්, එවිට කොස් 90 = 0 නිසා, පිලිතුර අනිවාර්යෙන්ම 0 වේ.

අදිශ ගුණිතය න්‍යාදේශ්‍ය න්‍යායට අනුකූල වේ.

a . b = b . a

අදිශ ගුණිතය විඝටන න්‍යායටද අනුකූල වේ. මෙහිදී වරහන තිබුණත් ඊට පිටතින් තිත තිබිය යුතු වෙනවා මොකද තිත් ගුණිතය බව තේරුම් ගන්නේ එම තිතෙනි. එනිසා, (a + b)c ලෙස ලිවිය නොහැකි අතර, (a + b) . c ලෙසම ලිවිය යුතුයි.

(a + b) . c = a . c + b . c

a . (b + c) = a . b + a . c

අදිශ ගුණිතය සඳහා සාමාන්‍යයෙන් සංඝටන න්‍යායක් ගැන කතා නොකරයි (එය ලිවිය හැකි ක්‍රමයක් නැති නිසා). a.b.c ලෙස දෛශික තුනක තිත් ගුණිතයක් ලිවිය නොහැකියි. ඒ මන්දැයි තර්ක කර බලන්න. එහි පළමු දෛශික දෙක අතර තිත් ගුණිතය සිදු කළ විට ලැබෙන්නේ අදිශයකි. එවිට එම අදිශය හා තෙවැනි දෛශිකය අතරයි දැන් තිත් ගුණිතය සිදු කරන්නට තිබෙන්නේ. එහෙත් අදිශයක් හා දෛශිකයක් අතර තිත් ගුණිතයක් සිදු කළ නොහැකිය.

කාටිසියානු පද්ධතිය ඇසුරින්ද අදිශ ගුණිතය පිළිබඳ ඉහත සඳහන් කළ සියලු ලක්ෂණ එලෙසම පෙන්විය හැකිය. මෙහිදී, තිත් ගුණිතය සිදු කරන විට, දෛශික දෙකෙහි අනුරූප සංරචක එකිනෙකට ගුණ කිරීම පමණයි කරන්නට තියෙන්නේ. උදාහරණයක් ලෙස, a = a₁i + a₂j + a₃k හා b = b₁i + b₂j + b₃k යන දෛශික දෙක ගත් විට පහත ආකාරයට තිත් ගුණිතය සිදු කෙරේ.

a . b = ( a₁i + a₂j + a₃k) . (b₁i + b₂j + b₃k) = a₁b₁ + a₂b₂ + a₃b₃

තවද, මෙහිදී එකිනෙකට ලම්භක/ප්‍රලම්භක දිශා පවතින නිසා පහත ආකාරයේ අපූරු ගතිලක්ෂණ පවතින බව ඔබට පහසුවෙන්ම වැටහේවි. පහත ගතිගුණවලින් ඉහත ප්‍රකාශය පහසුවෙන්ම වටහ ගන්නටත් පුලුවන්.

i . i = j . j = k . k = 1

i . j = i . k = j . k = 0

ඉහත සම්බන්දතා ලබා ගත් හැටි වැටහෙනවාද? i . i යනු එකම දිශාවට පවතින ඒකක දෛශික දෙකක්නෙ. එනිසා එය i² ලෙසත් අවශ්‍ය නම් ලිවිය හැකියි. මෙවිට, ඒ දෙක අතර කෝණය 0 වී, කොස් 0 = 1 නිසාත් ඒකක දෛශිකයක විශාලත්වයත් 1 නිසා, 1.1.1 = 1 බවට පත් වෙනවා නේද? එලෙසම i, j, k යන ඒකක දෛශික 3 එකිනෙකට ලම්භක වන නිසා, ඒ කියන්නේ කෝණය අංශක 90 නිසා, කොස් 90 = 0 වීම හේතුවෙන් එම ඒකක දෛශික 3න් ඕනෑම දෙකක් එකිනෙකට ගුණ වන විට 1.1.0 = 0 වේ.

දෛශික ගුණිතය

දෛශික ගුණිතයේදී (vector product) දෛශික දෙකක් ගුණ වී අවසාන පිලිතුර ලෙස ලබා දෙන්නේද දෛශිකයකි. මෙම ගණිත කර්මයේ සංකේතය x වේ. එනිසා එය "කතිර ගුණිතය" (cross product) ලෙසද හැඳින්වේ. කතිර ගුණිතයෙහි වැදගත් ලක්ෂණ 3ක් ඇත.

1. කතිර ගුණිතයෙන් ලැබෙන දෛශිකයේ විශාලත්වය හැමවිටම කතිර ගුණිතයට සහභාගි වූ දෛශික දෙකෙහි විශාලත්වයන් දෙකෙහි ගුණිතය, එම දෛශික දෙක අතර කෝණයෙහි සයින් අගයෙන්ද වැඩි කළ විට ලැබෙන අගයට සමාන වේ. උදාහරණයක් ලෙස, a හා b යන දෛශික දෙක කතිර ගුණිත කළ විට, පිලිතුරු දෛශිකයේ විශාලත්වය (||a||)(||b||)sinθ වේ.

පිලිතුරු දෛශිකය a x b වන බැවින්, එහි විශාලත්වය |a x b| ලෙස (සංකේතාත්මකව) ලිවිය හැකි අතර, (||a||)(||b||)sinθ යනු එම අගය ලබා ගැනීමට සුලු කරන සූත්‍රය වන අතර ඇත්තටම (ජ්‍යාමිතික වශයෙන් සලකන විට) ඉන් කියන්නේ චතුරස්‍රයේ/සමාන්තරාස්‍රයේ වර්ගපලය තමයි. පහත රූපයෙන් එය තවත් පැහැදිලි වේවි (යම් ත්‍රිකෝණයක වර්ගපලය එහි (පාදයxලම්භ උස)/2 නිසා, එවැනි ත්‍රිකෝණ දෙකක හෙවත් සමාන්තරාස්‍රයක වර්ගපලය (පාදයxලම්භ උස) විය යුතුයිනෙ).

2. කතිර ගුණිතයෙන් ලැබෙන දෛශිකයේ දිශාව වන්නේ හැමවිටම කතිර ගුණිතයට සහභාගි වූ දෛශික දෙකෙහිම දිශාවලට ලම්භක දිශාවකි. ඒ කියන්නේ a හා b දෛශික දෙක යම් ඍජුකෝණාස්‍රයක පාද දෙකක් යැයි සිතුවොත් එම දෛශිකවල විශාලත්වයන් ගුණ කිරීමෙන් ලැබෙන්නේ (|a|)(|b|) වර්ගපලය සහිත තලයකි (ඉහත රූපය). ඉතිං, කතිර ගුණිතයෙන් ලැබෙන පිලිතුරු දෛශිකයේ දිශාව වන්නේ මෙම තලයට ලම්භක දිශාවකි.

3. ඉහත දෙවැනි ලක්ෂණයෙන් කියවෙන දේ නිශ්චිත නැත. එනම්, පිලිතුරු දෛශිකය එම තලයට ලම්භක දිශාවක් ඔස්සේ පවතිනවා යැයි කිව්වත්, එම දිශාව තවම නිශ්චිත නැත මොකද තලයට ලම්භක දිශා දෙකක් තිබෙන නිසා (තලයට ඉහලින් ලම්භක හා පහලින් ලම්භක). එහෙත් මේ දිශා දෙකෙන් හරි දිශාව නිශ්චිතව දැන ගත හැකියි.

මෙහිදී, කතිර ගුණිතයට සහභාගි වන දෛශික දෙකෙන් (කතිරයට පෙර පවතින) පළමු දෛශිකය පවතින දිශාවේ සිට (කතිරයට පසුව පවතින) දෙවැනි දෛශිකය දෙසට දකුණතේ ඇඟිලි පහත රූපයේ ආකාරයට කරකවන විට, මාපට ඇඟිල්ල යොමු වූ ලම්භක දිශාව තමයි ගත යුත්තේ. මෙම ගුණය "a හා b දෛශික දෙක එක්කහුවී දකුණත් පද්ධතියක් (right-handed system) සාදනවා" යැයි කියනවා. බලන්න පහත රූපය. එම කතිර ගුණිතයේ පළමු දෛශිකය A වන නිසා, එම පැත්තේ සිට දෙවැනි B දෛශිකය දෙසට දකුණතේ ඇඟිලි කරකවන විට මාපට ඇඟිල්ල උඩට එස වේ. ඒ කියන්නේ පිලිතුරු දෛශිකයේ දිශාව එයයි.

ඉහත ලක්ෂණ 3ම එකට කැටි කොට කතිර ගුණිතය සංක්ෂිප්ත ආකාරයෙන් පහත සම්මත ස්වරූපයෙන් ලියනවා. එහි N̂ යනු ඒකක දෛශිකයකි (ඊට උඩින් හැට් එකක් දැමීමෙන් එය ඒකක දෛශිකයක් බව හඟවනවා). මෙම N යන අකුරින් මතක් කර දෙන්නේ එය ලම්භක (normal) බවයි (ඉහත විස්තර කළ පරිදි දකුණත් පද්ධතියක් බවද ඉන් හඟවනවා). එනිසා මෙම N මඟින් දෛශිකයේ අගයට කිසිම බලපෑමක් එල්ල නොකරයි; දිශාව ගැන පමණක් හඟවයි. ඒ අනුව පැහැදිලි වෙනවා N යෙදීම නිසා තමයි විශාලත්වයක් පමණක් තිබූ පිලිතුර දෛශිකයක් බවට පත් වන්නේ (මොකද දෛශිකයක් වීමට දිශාව අත්‍යවශ්‍ය නිසා).

දෛශික ගුණිතය හැමවිටම දකුණත් පද්ධතියකි. ඒ කියන්නේ ගුණිතයේ දෛශික පද දෙක ලියන අනුපිලිවෙල වැදගත් වේ. මේනිසා දෛශික ගුණිතයේදී න්‍යාදේශ්‍ය න්‍යාය වලංගු නොවේ. එ් වෙනුවට පහත ආකාරයේ සම්බන්දතාවක් ඇත. එනම්, දෛශික දෙක මාරු කළ විට, ලැබෙන අගය එකම වුවත් සලකුණින් ප්‍රතිවිරුද්ධ වේ. මෙම ගතිගුණය ප්‍රති-න්‍යාදේශ්‍ය න්‍යාය (anti-commutative law) ලෙස හැඳින්විය හැකිය.

a x b = - (b x a) 

 

එහෙත් දෛශික ගුණිතය විඝටන න්‍යාය පිලිපදී.

(a + b) x c = (a x c) + (b x c)

a x (b + c) = (a x b) + (a x c)

මෙය සංඝටන න්‍යාය පිලිපදින්නේ නැත. එකම දිශාව ඔස්සේ හෝ එකිනෙකට ප්‍රතිවිරුද්ධ දිශා ඔස්සේ පවතින දෛශික දෙකක කතිර ගුනිතය හැමවිටම ශූන්‍ය වේ. ඊට හේතුව මෙවිට කෝණ අගය 0 හෝ 180 වන බැවින් එම කෝණවල සයින් අගය 0 වීමයි. ගුණිත අගය උපරිමයට පත් වන්නේ දෛශික දෙක එකිනෙකට ලම්භක වන විටයි.

දැන් බලමු කාටිසියානු ඛණ්ඩාංක පද්ධතිය ඇසුරින් කතිර ගුණිතය ගැන ඉහත සාකච්ඡා කළ දේවල් නැවතත්.

a x b = (a₁i + a₂j + a₃k) x (b₁i + b₂j + b₃k) = (a₂b₃ - a₃b₂)i + (a₃b₁ - a₁b₃)j + (a₁b₂ - a₂b₁)k

ඉහත ගුණ කිරීම තරමක් දිගු වේ. එහෙත් එහි යම් රටාවක් ඇත. i සංරචකය හෙවත් පළමු සංරචකයේ වරහන තුල යටකුර (subscript) 1 වන කිසිදු පදයක් හමු නොවී අනෙක් 2, 3 යන යටකුරු දෙක හමු වේ (යටකුරක් යනු යම් පදයකට පසුව යටින් කුඩාවට ලියන අක්ෂරය හෝ ඉලක්කමයි). එලෙසම දෙවැනි සංරචකය තුල යටකුර 2 වන කිසිදු පදයක් හමු නොවී, 1, 3 යන යටකුරු දෙක හමු වේ; තෙවැනි සංරචකයෙත් එම ගුණය ඇත. තවද, වරහන තුල ඇති හැම පදයකම මුලින් ඇත්තේ කතිර ගුනිතයේ පළමු දෛශිකයට අයත් කොටසයි (රතුපාටින් දක්වා ඇත); දෙවැනියට ඇත්තේ දෙවැනි දෛශිකයට අයත් කොටසයි. තවද, එම යටකුරු සහිත කොටස් සංරචකයෙන් සංරචකයට පිලිවෙලින් යද්දී 2-3-1-2-3- ආදි ලෙස චක්‍රීයව යටකුරු වෙනස් වේ (යටින් ඉරි ගසා ඇති කොටස බලන්න; උඩින් ඉරි ගසා ඇති කොටස බලන්න; එලෙසම අනෙක් කොටසුත් බලන්න).

ඉහත විස්තර කළ රටාව අනුගමනය කරමින් යන විට කතිර ගුණිත ප්‍රකාශය ලැබෙනවාදැයි චෙක් කර බලමු. පියවරින් පියවර යමු.

(ab - ab)i + (ab - ab)j + (ab - ab)k

(a₂b - ab)i + (a₃b - ab)j + (a₁b - ab)k

(a₂b₃ - ab)i + (a₃b₁ - ab)j + (a₁b₂ - ab)k

(a₂b₃ - a₃b)i + (a₃b₁ - a₁b)j + (a₁b₂ - a₂b)k

(a₂b₃ - a₃b₂)i + (a₃b₁ - a₁b₃)j + (a₁b₂ - a₂b₁)k

සටහන

න්‍යාස

ගණිතයේදී න්‍යාස (matrix) යනුවෙන් සංකල්පයක් හමු වේ. දළ වශයෙන් න්‍යාසයක් යනු ක්‍රමවත් රටාවකට ලියා තබන අගයන් සමූහයකි. එම අගයන් නිකංම එහෙන් මෙහන් තමන්ට කැමති පරිදි දැමූ අගයන් නොවේ. න්‍යාස ස්වරූපයෙන් අපට හැකියි එකවරම අගයන් රාශියක් සමඟ වැඩ කරන්නට. න්‍යාස සඳහා වෙනමම ගණිත කර්ම රාශියක් නිර්වචනය කර ඇත. සාමාන්‍යයෙන් න්‍යාස පහත ආකාරයෙන් සටහන් කර තබනවා.

න්‍යාසයක් ඇතුලේ තිබෙන පද "අවයව" (elements) ලෙස හැඳින්වෙනවා. එම අවයව ඉහත ආකාරයට ඉරි කැබැලි දෙකක් හෝ කොටු වරහන් දෙකක් තුල ලිවිය යුතුය. න්‍යාසයක පේලි ගණනයට තීරු ගණන සමාන වීම අවශ්‍ය නොවේ. එහෙත් යම් පේලියක හෝ තීරුවක පදයක් හිස් නොවී තිබිය යුතුය. න්‍යාස ගැන දැනුමක් නැතිනම් ඒ ගැන ඉගෙන ගන්න.

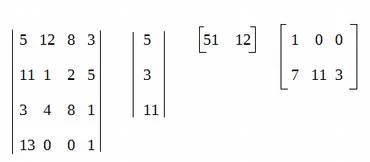
ඉහත පෙන්වා ඇති දිගු ගණිතමය ප්‍රකාශය පහසුවෙන්ම න්‍යාසයක් ආකාරයෙන් ඉදිරිපත් කළ හැකිය (පහත රූපය). න්‍යාස ගැන ඔබ දන්නවා නම්, එම න්‍යාසය ප්‍රසාරණය කළ විට ඉහත දිගු කතිර ගුණිත ප්‍රකාශයම ලැබෙන බව පෙනේවි.

කතිර ගුණිතයේදී i, j, k යන ඒකක දෛශික අතර පහත ආකාරයේ සම්බන්දතා පවතී.

i x i = j x j = k x k = 0

i x j = k j x i = -k

j x k = i k x j = -i

k x i = j i x k = -j

ඉහත අවසාන සම්බන්දතා ටික චක්‍රීය බවක් පෙන්වයි (එනම්, i-j-k-i-j- ආදී ලෙස පිලිවෙලින් ගමන් කරනවා; පිලිවෙලින් ඇති ඒකක දෛශික දෙකක් ගුණ කරන විට, අනෙක් ඒකක දෛශිකය ලැබේ). ප්‍රති-න්‍යාදේශ්‍ය න්‍යාය පිලිපඳින නිසා x ට දෙපස ඇති ඒකක දෛශික දෙක මාරු කරන විට ඍන සලකුණ ලැබේ.

මෙතෙක් සලකා බැලුවේ දෛශික දෙකක ගුණිත පමණි. ඇත්තෙන්ම එය තමයි ඉතා ඕනකමින් දැන සිටිය යුත්තෙත්. දෛශික 3ක් එකිනෙකට ගුණ කළ හැකි අවස්ථාද තිබෙනවා. එහෙත් මෙහිදී සීමාවන් තිබෙනවා. එම සීමාවන් ඔබටම තර්ක කර හැඳින ගත හැකියි. දෛශික තුනක ගුණිත ගැන මා විස්තර කරන්නේ නැති වුවත්, තර්ක කර එම අවස්ථා මොනවාදැයි පමණක් පෙන්වන්නම්. ඇත්තෙන්ම අමුතුවෙන් දෛශික 3ක් හෝ 4ක් හෝ සුලු කරන හැටි ඉගෙන නොගෙන වරකට දෛශික 2 බැඟින් ගෙන ඔබ මෙතෙක් ඉගෙන ගත් ක්‍රම ඔස්සේ සුලු කිරීම් සිදු කළ හැකියි.

තිත් ගුණිතයෙන් ලැබෙන්නේ අදිශයක් බැවින්, වරක් එය සිදු කළ පසු, නැවත තවත් දෛශිකයක් සමඟ තිත් ගුණිතයක් හෝ කතිර ගුණිතයක් සිදු කළ නොහැකිය මොකද තිත් හෝ කතිර ගුණිතයේදී අනිවාර්යෙන්ම දෛශික දෙකක්ම ගුණ විය යුතු නිසා. එහෙත් තිත් ගුණිතයකින් ලැබෙන අදිශය තවත් දෛශිකයක් සමඟ දෛශික ගුණාකාරය සිදු කළ හැකියි. ඒ අනුව,

(a . b) . c - අවලංගුයි (සිදු කළ නොහැකියි)

(a . b) x c - අවලංගුයි (සිදු කළ නොහැකියි)

(a . b)c - වලංගුයි (සිදු කළ හැකියි)

කතිර ගුණිතයකින් ලැබෙන්නේ දෛශිකයක් බැවින්, වරක් එය සිදු කළ පසු, නැවත තවත් දෛශිකයක් සමඟ තිත් ගුනිතයක් හෝ කතිර ගුණිතයක් සිදු කළ හැකියි. තවද, එය දෛශික ගුණාකාරයද සිදු කළ හැකියි. ඒ අනුව,

(a x b) . c - වලංගුයි (සිදු කළ හැකියි)

(a x b) x c - වලංගුයි (සිදු කළ හැකියි)

(a x b)t - වලංගුයි (සිදු කළ හැකියි); එහෙත් මෙහි දෛශික 3ක් නැති නිසා නොසලකා හැරේ.