දෛශික (vectors) - 1

එදිනෙදා ජීවිතයේදිත් විද්‍යාවේදිත් අපට විවිධාකාරයේ අගයන් සමඟ කටයුතු කිරීමට සිදු වෙනවා. ඉන් සමහරක් නිකංම සංඛ්‍යාවකින් ප්‍රකාශ කළ හැකි අගයන්ය. අඹ ගෙඩි 4ක්, ළමයි 6 දෙනෙක් ආදී ලෙස ඒවා ප්‍රකාශ කළ හැකියි. තවත් සමහර අවස්ථාවලදී නිකංම අගයකින්/සංඛ්‍යාවකින් පමණක් ප්‍රකාශ කළ නොහැකි දේවල්/රාශි (quantity) හමු වේ. මෙවිට “මීටර්”, “තත්පර”, “කිලෝග්‍රෑම්” වැනි යම් ඒකකයක් (unit) සමඟ එම අගයන් පැවසිය යුතුය; නැතිනම් ප්‍රකාශ කරන අදහස නිශ්චිත නොවේ. උදාහරණයක් ලෙස, “මං 5කින් එන්නම්” යැයි කී විට, එම 5 යනු තත්පරද, පැයද, දවස්ද, අවුරුදුද ආදි ලෙස නිශ්චිත නොවේ. මේ දෙවර්ගයේම අගයන් අදිශ (scalar) ලෙස හැඳින්වේ. අදිශයක් හෙවත් අදිශ රාශියක් යනු විශාලත්වයක් පමණක් ඇති දිශාවක් නැති අගයන්ය. ඔබේ වයස කියන විට, “උතුරට 24යි, නැගෙනහිරට 16යි” කියා කියන්නේ නැහැනෙ මොකද දිශාව යන සාධකය/කාරණය වයස නමැති රාශියට වැදගත්කමක් නැත.

එහෙත් සමහර අවස්ථා තිබෙනවා අගයක්/විශාලත්වයක් (magnitude) මෙන්ම දිශාවක්ද (direction) පැවසීමට සිදු වන. මෙවැනි රාශි දෛශික (vector) ලෙස හැඳින්වේ. උදාහරණයක් ලෙස, ඔබ යම් “බලයක්” යොදා මේසයක් මත තිබෙන පොතක් වැනි වස්තුවක් තල්ලු කරන විට, එය තල්ලු කරන්නට යොදන බලයේ විශාලත්වයක් මෙන්ම එය තල්ලු කරනගෙන යන දිශාවක්ද ඇත. එනිසා බලය යනු දෛශික රාශියකි. දෛශික සඳහා සෑම විටම (නිව්ටන්, තත්පරයට මීටර් ආදී) ඒකකයක් තිබේ.

විද්‍යාවේදී බොහෝ දෛශික රාශි හමු වේ. විස්ථාපනය (displacement), ප්‍රවේගය (velocity), ත්වරණය (acceleration), බලය (force), පීඩනය (pressure), ගම්‍යතාව (momentum), විදුලි ධාරාව (electric current), ව්‍යාවර්තය (torque) ආදි රාශි ඊට උදාහරණ වේ. විද්‍යාව තුල අදිශ රාශිද ගණනාවක් ඇත – කාලය (time), දුර (distance), වේගය (speed), ශක්තිය (energy), ක්ෂමතාව (power).

අදිශයක් වේවා දෛශිකයක් වේවා, මෙවැනි රාශි අගයන් සමඟ විවිධ ගණනය කිරීම් (ගණිත කර්ම) සිදු කළ හැකිය. එකතු කිරීම හෙවත් ආකලනය (addition), අඩු කිරීම හෙවත් ව්‍යාකලනය (subtraction), ගුණ කිරීම (multiplication), බෙදීම (division), මූල සෙවීම (root), බලයකට නැංවීම (exponentiation), අවකලනය කිරීම (differentiation), අනුකලනය කිරීම (integration) යනු නිතරම අප භාවිතා කරන ගණිත කර්ම වේ. මේ සඳහන් කළ සියලු ගණිත කර්ම ගැන හොඳ අවබෝධයක් හා අදිශ සමඟ මෙම ගණිත කර්ම සිදු කරන හැටි ඔබ දැනටමත් දන්නවා යැයි මා උපකල්පනය කරනවා (දන්නේ නැතිනම්, පළමුව ඒවා ගැන ඉගෙන ගන්න). මෙම පාඩම් මාලාව තුල මෙම ගණිත කර්ම දෛශික සමඟ විශේෂයෙන් යොදා ගන්නා ආකාරය ගැන විමසා බලනවා. දෛශික ගැන ඉගෙන ගන්නවා යනු ඇත්තටම එයම තමයි.

අදිශයක් කොලයක් මත සටහන් කරන්නේ නිකංම අගයක් ලෙසයි (ඒකකයක්ද අගයට පිටුපසින් තිබිය හැකියි) - 4, 23km, 732kg, 344,300 ආදි ලෙස. බොහෝවිට කෙලින්ම අගයක් වෙනුවට විචල්‍යයක් (variable) ආකාරයෙන්ද එම අදිශ අගයන් ඉදිරිපත් කෙරෙනවා (x, a ආදි ලෙස). දෛශිකයක් ලියන විට, විචල්‍යය තද (bold) අකුරින් (x, a ආදි ලෙස) ලිවිය යුතුය. පරිගනකයක් මඟින් ලියන විට ඉතාම පහසුවෙන්ම අකුරු තද/බෝල්ඩ් කළ හැකි වුවත්, අතින් ලියන විට එය කිසිසේත් පහසු නැත. එනිසා ප්‍රායෝගික භාවිතය සඳහා ඉතා පහසු ක්‍රමයක් හඳුන්වා දී තිබෙනවා. එනම්, දෛශිකයට ඉහලින් කුඩා තිරස් ඉරි කැබැල්ලක් (bar) හෝ ඊතල හිසක් දැමිය හැකිය (x, a ආදි ලෙස). සමහරු අක්ෂරයට යටින්ද ඉරි කැබැල්ල ගසති.

මීටත් අමතරව දෛශිකයක් රූපමය ආකාරයකින්ද නිරූපණය කළ හැකියි පහත දැක්වෙන ලෙස. ඊතලයේ දිගින් දෛශිකයේ විශාලත්වයද, ඊතලය ඇඳ තිබෙන දිශාවෙන් දෛශිකයේ දිශාවද නිරූපණය කෙරේ. මෙය බැලූ බැල්මට ඉතා පහසුවෙන් තේරුම් ගත හැකි වුවත්, ගණනය කිරීම් සඳහා උචිත ක්‍රමයක් නොවේ.

දෛශිකයක විශාලත්වය “ඒකක” 1ක් ලෙස ගත් විට, ඊට “ඒකක දෛශිකයක්” (unit vector) කියා කියනවා. ඒ කියන්නේ දැන් දෛශිකයේ විශාලත්වය 1යි. උදාහරණයක් ලෙස, යම් විස්ථාපනයක (දුරක) විශාලත්වය 1ක් නම්, එවිට එය ඒකක දෛශිකයකි. මෙවිට ඔබ අසාවි 1 යන අගය නිශ්චිත නැහැ නේද කියා. ඒ කියන්නේ එම අගය අඟල් 1ක්ද, මීටර් 1ක්ද, සැතපුම් 1ක්ද, ආලෝක වර්ෂ 1ක්ද කියා ඔබ නොදනී. ඇත්තටම මෙහිදී 1 යනු ඔබ සලකා බලනු ලබන මෙවැනි ඕනෑම ඒකකයකින් 1කි. ඒ කියන්නේ ඔබ විස්ථාපනය ගණනය කරන්නේ සැතපුම්වලින් නම්, ඒකකයක් හෙවත් ඒකක 1ක් යනු සැතපුම් 1කි දැන්. එබ සලකා බැලුවේ මීටර්වලින් නම්, ඒකකයක් යනු මීටර් 1කි.

ඇත්තටම විද්‍යාව තුල බොහෝ අර්ථ දැක්වීම් සිදු කරන්නේ මෙවැනි “ඒකක” විශාලත්වයක් සඳහාය (බලන්න විද්‍යා සංකල්ප කිහිපයක් අර්ථ දැක්වීම්). මෙලෙස ඒකක විශාලත්වයක් ගත් විට, අර්ථ දැක්වීම පොදු ස්වභාවයක් ගනී. එමඟින් යම් නිශ්චිත ඒකකයකට (කිලෝග්‍රෑමයකට හෝ මීටරයකට වැනි) එම අර්ථ දැක්වීම කොටු කිරීම වැලැකේ. ඒකක දෛශිකයක් ගත් විටත්, එහි ඇති “ඒකක” යන වචනය තේරුම් ගත යුත්තේ මේ අයුරින් තමයි.

එසේ වුවත්, අර්ථ දැක්වීම් තුලදී මෙලෙස “ඒකක 1ක්” යන්න එම රාශිය මනින සම්මත ඒකකයෙන් 1ක් ලෙස වුවද ගත හැකිය. උදාහරණයක් ලෙස, “ඒකක ස්කන්ධයක්” කී විට එය කිලෝග්‍රෑම් 1ක් ලෙසද, “ඒකක කාලයක්” කී විට එය තත්පර 1ක් ලෙසද ආදි ලෙස ගත හැකිය. ඔබ දන්නවා විද්‍යාව තුල සෑම මිනුමක් සඳහාම සම්මත ඒකකයක් තිබෙනවා.

ඒකක දෛශිකයක් යනු යම් නිශ්චිත දිශාවක් ඔස්සේ පවතින අගය/විශාලත්වය ඒකක 1ක් වන රාශියකි. එය දක්වන්නේ දෛශිකය නිරූපණය කරන විචල්‍යයට ඉහලින් කුඩාවට ˆ වැනි සංකේතයක් (මෙම සංකේතය circumflex ලෙස හැඳින්වෙන අතර, එය අක්ෂරයක් මතට යෙදූ විට hat යන නමින් උච්චාරණය කෙරේ) යෙදීමෙනි (â ආදි ලෙස; “ඒ හැට්” ලෙස එය උච්චාරණය කෙරේ).

යම් a නම් දෛශිකයක් ගත්විට, “a නම් දෛශිකයේ විශාලත්වය” යන්න කෙටි සංකේතාත්මකව නිරූපණය කරන්නේ ||a|| ලෙසයි. දෛශිකයේ විශාලත්වය |a| ලෙසද දැක්විය හැකියි. සමහරු දෛශිකය කැපිටල් ඉංග්‍රිසි අකුරකින් දක්වා එහි විශාලත්වය එම අක්ෂරයේම සිම්පල් අකුරින් දක්වනවා.

යම් දෛශිකයක් එම දෛශිකයේ විශාලත්වයෙන් බෙදූ විට අපට ලැබෙන්නේ ඒකක දෛශිකය තමයි.

ගණිතයේදී/විද්‍යාවේදී යම් රාශියක් ගෙන, එය යම්කිසි ක්‍රමයකින් “ඒකක 1ක” විශාලත්වයක් බවට පත් කළ විට (ඉහත ආකාරයට යම් අගයකින් බෙදා), ලැබෙන අවසාන අගයට (පිලිතුරට) “ප්‍රමතකෘත” (normalized) අගයක්/රාශියක් යැයි කියනවා. ඒ අනුව ඒකක දෛශිකයම “ප්‍රමතකෘත දෛශිකය” (normalize vector) ලෙසද හැඳින්විය හැකියි.

මෙවිට, ඒකක දෛශික නිරූපණය ඇසුරින් ඕනෑම දෛශිකයක් දැක්විය හැකිය (මෙහි ප්‍රයෝජනය මොහොතකින් පැහැදිලි වේවි). උදාහරණයක් ලෙස, 20â යනු â නම් ඒකක දෛශිකය මෙන් 20 ගුණයක් විශාල දෛශිකයකි. ඉතිං â හි සත්‍ය විශාලත්වය හා දිශාව දන්නේ නම් 20â හි විශාලත්වය හා දිශාව පහසුවෙන්ම ලැබේ (එනම්, නිකංම එමෙන් 20 ගුණයක් විශාල දෛශිකයක් ලෙස සලකන්නටයි තිබෙන්නේ).

දෛශිකයක දිශාව ගැනද විශේෂයෙන් හොඳ අවබෝධයක් ඇති කර ගත යුතුය. සාමාන්‍ය ජීවිතයේදී උතුර, නැගෙනහිර, බටහිර, දකුණ, උඩ, යට ආදි ලෙස යම් නිශ්චිත දිශා කිහිපයක් අප භාවිතා කරනවානෙ. ගණිතයේදී/විද්‍යාවේදී එය කිසිසේත් ප්‍රමාණවත් නැත. එනිසා දෛශිකවල දිශාව පැවසීමට ඉතා හොඳ ක්‍රමයක් භාවිතා කෙරේ. එය නම් ඛණ්ඩාංක පද්ධතිය (coordinate system) වේ. ඛණ්ඩාංක පද්ධතියක් මඟින් යම් රාශියක් අවකාශයේ පිහිටීම් මෙන්ම එහි දිශාවද 100%ක් නිවැරදිව හා නිශ්චිතව ප්‍රකාශ කළ හැකිය.

ඛණ්ඩාංක පද්ධතිද කිහිපයක්ම තිබේ. එහෙත් ඊට පෙර අවකාශය (space) යන සංකල්පය ගැන දැනගනිමු. දළ වශයෙන් අවකාශය යනු යමකට චලනය විය හැකි වටපිටාව යනුවෙන් කෙනෙකු හැඳින ගත්තාට වරදක් නැත. ඔබ අප උපන්දා සිට හැසිරෙන්නේද මෙවන් අවකාශයක් තුලයි. ඔබට දැන් ඔය සිටින තැන සිට වමට හෝ දකුණට චලනය විය හැකිය; ඉදිරියට හෝ පසුපසට චලනය විය හැකිය; උඩට හෝ යටට චලනය විය හැකියි. එනම් එකිනෙකට සම්පූර්නයෙන්ම ස්වාධීන දිශා 3ක් ඔස්සේ ඔබට චලනය විය හැකිය. එනිසා එය ත්‍රි-මාන අවකාශයක් (3 dimensional space) ලෙස හඳුන්වමු. ඇත්තටම අපට ඉතාම හුරුපුරුදු වන්නේ 3D අවකාශයයි.

එහෙත් සෛද්ධාන්තිකව ඊට වඩා අඩු ද්විමාන (2 dimensional), ඒකමාන (1 dimensional) ලෙස අවකාශද, ඊට වඩා වැඩි චතුර්මාන (4 dimensional), පංචමාන ආදි ලෙස අනන්තය තෙක් මාන ඇති අවකාශයන් ගැන කතා කළ හැකිය.

ත්‍රිමාන අවකාශයක් එකිනෙකට ලම්භක දිශා 3ක් ඔස්සේ පවතින්නකි (සාමාන්‍යයෙන් එම එකිනෙකට ලම්භක දිශා 3 අප දිග, පලල, උස ලෙස හඳුන්වන්නට පුරුදුව සිටිනවා). මෙය මඳක් විමසා බලමු. කෙනෙකු කිව හැකියි මෙම දිශා 3ට අමතරව තවත් දිශා ඕනෑ තරමක් ඊට ඇතුලත් කළ හැකියිනෙ කියා. ඔව්, ඇතුලු කළ හැකියි, නමුත් එලෙස ඇතුලු කරන අමතර දිශාවන් අර අනෙක් දිශාවලට ලම්භක නොවේවි.

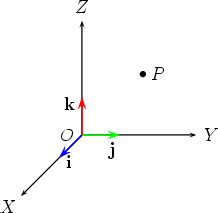
ඛණ්ඩාංක තලයේ එම දිශා (එනම් යම් දිශාවක් ඔස්සේ ගමන් කළ හැකි දුර) එකිනෙකට ලම්භක වීම ඉතාම වැදගත් අවශ්‍යතාවකි. එහි සැබෑ අර්ථය බොහෝ දෙනෙක් සිතන්නේ නැත. ඉහත රූපය බලන්න. එහි x දිශාව ඔස්සේ ගමන් කරනවා යැයි සිතමු. එම දිශාව ඔස්සේ ධන පැත්තට හෝ ඍණ පැත්තට කොතරම් ගමන් කළත් y දිශාව ඔස්සේ “ඇබිත්තක්වත්” ගමන් කිරීමක් සිදු වන්නේ නැහැ නේද? එලෙසමයි y දිශාව ඔස්සේ කොතරම් ගමන් කළත් x දිශාව ඔස්සේ කිසිදු චලිතයක් සිදු නොවනු ඇති. ඛණ්ඩාංක තලයකදී ලම්භක යැයි පවසන්නේ මෙම ගති ගුණයයි (එහෙම නැතිව අර ජ්‍යාමිතියේදී අක්ෂ දෙකක් අංශක 90කින් කැපෙන සේ පිහිටි විට ඒ දෙක ලම්භකයි කියන අර්ථයෙන් නොවේ). ඇත්තෙන්ම මේ දැන් හැඳින ගත් ගුණයට කියන ඉංග්‍රිසි orthogonal යන වචනයට සුදුසු සිංහල වචනය ප්‍රලම්භක යන්නයි. මෙම ප්‍රලම්භක ගුණයම ගණිතයේ වෙනත් තැනක රේඛීය ස්වායත්තභාවය (linearly independence) ලෙස හැඳින්වෙන අදහසට සමාන වේ.

ඉතිං, ත්‍රිමාණ අවකාශය සලකන විට, ප්‍රලම්භක ගුණය පවතින සේ ඇඳිය හැකි ඛණ්ඩාංක අක්ෂ ගණන 3කි. එම අක්ෂ 3 x, y, z ලෙස සාමාන්‍යයෙන් සලකුණු කෙරේ. එය අඳින පිලිවෙලක්ද ඇත. එනම්, දෙපැත්තේ ඊහිස් සහිත යම් ඍජු සරල රේඛාවක් ඇඳ එය x අක්ෂය (axis) ලෙස නම් කරන්න. ඉන්පසු ඊට ජ්‍යාමිතික වශයෙන් ලම්භකව තවත් අක්ෂයක් ඇඳ එය y අක්ෂය ලෙස නම් කරන්න. එම අක්ෂ දෙක කැපෙන ස්ථානය මධ්‍ය ලක්ෂ්‍යය හෙවත් කේන්ද්‍රය (origin) වේ. කේන්ද්‍රයේ සිට එක් පැත්තකට ධනද අනෙක් පැත්තට ඍණද වේ. මෙම කේන්ද්‍රය හරහා යන සේ අනෙක් z අක්ෂයද අර අක්ෂ දෙකටම ලම්භකව අඳින්න/සාදන්න. දැන් x හි ධන පැත්තේ සිට y හි ධන පැත්ත දක්වා දකුණතේ ඇඟිලි පහත රූපයේ දැක්වෙන සේ වක් කර ගත් විට, මාපට ඇඟිල්ල දික් වී තිබෙන පැත්ත තමයි z හි ධන පැත්ත වන්නේ.

මෙලෙස දකුණතේ මාපට ඇඟිල්ලෙන් දිශාව සොයා සකස් කර ගත් ඛණ්ඩාංක පද්ධතිය දකුණත් ඛණ්ඩාංක පද්ධතියක් (right-handed coordinate system) ලෙස හැඳින්වෙන අතර, එලෙසම වම් අත භාවිතා කළ විටත් ඛණ්ඩාංක පද්ධතියක් ලැබෙන අතර එය වමත් ඛණ්ඩාංක පද්ධතියක් (left-handed coordinate system) ලෙස හැඳින්වෙනවා. බහුල වශයෙන් භාවිතා කෙරෙන්නේ දකුණත් පද්ධතියයි. මෙම දෙකෙහි විශාල වෙනසක් පවතින බව පහත රූපය බැලූ විට පැහැදිලි වේ (දිශාවල වෙනසක් ඇත).

ඉහත ආකාරයට ඛණ්ඩාංක පද්ධතියක් සකසන ආකාරය මුලින්ම හඳුන්වා දුන්නේ රෙනේ ඩෙකාට් (René Descartes) විසින් වන අතර, එනිසා ඔහුට ගෞරව පිනිස එය කාටිසියානු ඛණ්ඩාංක පද්ධතිය (Cartesian coordinate system) ලෙස හැඳින්වේ. මේ හැරුණහම තවත් ඛණ්ඩාංක පද්ධති කිහිපයක්ම ඇති අතර, ඒ ගැන පසුවට විමසා බලමු.

ත්‍රිමාන අවකාශය අවබෝධ කර ගැනීමට කිසිසේත් අපහසු නොවුණත්, ද්විමාන අවකාශයක් ගැන ඔබට සිතා ගත හැකිද? ඔබ දන්නා ද්විමාන වස්තුන් මොනවාද? (මා නම් කිසිවක් දන්නේ නැත). මෙහිදී දිගක් හා පලලක් පමණක් තිබේවි (උසක්/ගනකමක්/ගැඹුරක් නැත). එහෙත් ටිකක් කල්පනා කළ විට ද්විමාන අවකාශය කෙබදු වනු ඇත්දැයි සිතෙන් මවා ගත හැකියි (සැබැවින් අත්දැකිය නොහැකි වුවත්). මේසය මත ඩික්ෂනරියක් මෙන් විශාල පොතක් තිබේ යැයි සිතන්න. එහි දිගක්, පලලක්, උසක් ඇත. එහෙත් දැන් එම ඩික්ෂනරියෙන් එක් කොලයක් කඩාගෙන එය මේසය මත තිබේ යැයි සිතන්න. කොලයක් සාමාන්‍යයෙන් ඉතා සිහින්නෙ (එනම් උස ඉතා කුඩාය). දැන් එම කොලයේ ගනකම තව තවත් අඩු කරගෙන යනවා යැයි සිතන්න. යම අවස්ථාවකදී එහි ගනකම ශූන්‍ය කළා යැයි සිතමු. එවිට එහි ගනකමක් ඇත්තේම නැති නිසා, දිගක් හා පලලක් පමණක් ඇති නිසා එය ද්විමාන වස්තුවක් බවට පත්ව ඇත. ද්විමාන ලෝකය කෙබඳු වනු ඇත්දැයි කල්පනා කර හා මිතුරන් සමඟ සාකච්ඡා කර බලන්න (සමහරවිට හොඳ විද්‍යා ප්‍රබන්දයක් වුවද රචනා කිරීමට හැකි වනු ඇති).

එය සිතින් මවා ගත නොහැකි නම්, තවත් හොඳ උපමාවක් කියන්නම්. සෙවනැල්ලක් ගැන සිතන්න. සෙවනැල්ල බිම මත පැතිරී තිබෙනවානෙ. ඒ කියන්නේ දිගක් හා පලලක් තිබෙනවා හෙවත් ක්ෂේත්‍රඵලයක් තිබෙනවා. එහෙත් සෙවනැල්ලේ කිසිදු ගනකමක් නැත. ගනකමක් තිබුණා නම් සෙවනැලිවල කකුල පැටලී අප තැන තැන ඇදගෙන වැටෙන්නට තිබුණා. පාරේ වේගයෙන් යන වාහන වෙනත් වාහනවල සෙවනැලිවල හැපී අනතරු ඇති විය හැකිව තිබුණා. සෙවනැල්ල යනු වස්තුවක් නොවුණත්, ද්විමාන අවකාශය වටහා ගැනීමට එය කදිම උපමාවක්.

ඉතිං කාටිසියානු ඛණ්ඩාංක පද්ධතිය යොදා ගත හැකියි ද්විමාන අවකාශයක් නිරූපණය කිරීම සඳහාත්. මුලින් අප දුටුවේ ත්‍රිමාන කාටිසියානු ඛණ්ඩාංක පද්ධතියක් වන අතර, එහි z අක්ෂය ඉවත් කළ විට ලැබෙන්නේ ද්විමාන කාටිසියානු ඛණ්ඩාංක පද්ධතියක්/තලයක් වේ. ද්විමාන පැතිරීමකට/ක්ෂේත්‍රපලයකට අප තලයක් (plane) කියා කියනවානෙ.

මෙලෙසම ඒකමාන අවකාශය ගැනත් කල්පනා කර බලන්න. එහි පවතින්නේ එක් දිශාවක් ඔස්සේ පවතින දිගක් පමණි. එය හරියට සිහින් නූලක් වැනිය. නූලේ ගනකම ශූන්‍ය කළ විට දිග පමණක් ඉතිරි වන හැටි සිතින් මවා ගන්න. සංකල්පීය වශයෙන් ගත් විට ගණිතයේදී හමුවන සරල රේඛා ඒකමාන වේ. එහෙත් පොතේ ප්‍රායෝගිකව ඒකමාන නිර්මාණයක් සිදු කළ නොහැකි බැවින් පලලක් හා ගනකමක් සහිත සිහින් පැන්සල් හෝ පෑන් ඉරකින් එය අප අඳිනවා.

ඒකමාන අවකාශය සඳහා අමුතුවෙන් ඛණ්ඩාංක පද්ධති නැත. නිකමට හෝ කාටිසියානු පද්ධතිය මේ සඳහා සකස් කර ගන්නට සිතුවොත් ලැබෙන්නේ හුරුපුරුදු සංඛ්‍යා රේඛාව වේ.

දැන් ත්‍රිමානයට වඩා වැඩි මාන ගණනක් තිබෙන අවස්ථා ගැන සිතා බලන්න. ඇත්තටම අඩුම වශයෙන් සිතින්වත් ඒවා මවා ගත නොහැකිය. නිකංම වචනවලින් පංචමාන, අෂ්ටමාන ආදි ලෙස නම් කළ හැකිය; සූත්‍ර වල දමා සුලු කළ හැකිය; එහෙත් ඇඳීමට හෝ සිතෙන් මවා ගත නොහැකිය. අවකාශීය මාන ඕනෑම ගණනක් (n ගණනක්) සහිත අවකාශය හිල්බර්ට් අවකාශය (Hilbert space) ලෙස නම් කරනවා. එනිසා ත්‍රි-මානෙන් ඉහල මාන සඳහා ඛණ්ඩාංක පද්ධති ඇඳිය නොහැකිය.

මේ අනුව දෛශිකයක දිශාව ඕනෑම ඛණ්ඩාංක පද්ධතියක් ඇසුරින් දැක්විය හැකිය. මෙතෙක් සලකා බැලුවේ කාටිසියානු ඛණ්ඩාංක පද්ධතිය ගැන පමණක් නිසා, ඒ ඇසුරින් දෛශික දිශාව (හා විශාලත්වය) පෙන්වන අයුරු දැන් බලමු. ඒකක දෛශික යන සංකල්පය යොදා ගැනීමට සිදු වේ. එහිදී x අක්ෂය දිගේ ඒකක දෛශිකයක් අර්ථ දක්වා ගන්නා අතර, එය î (“අයි හැට්”) යන සංඛේතයෙන් දක්වනවා. ඒ අනුව x අක්ෂය ඔස්සේ යම් දෛශිකයක් 29î ලෙස ලිවිය හැකියි. හැමවිටම හැට් එක දැමීම කරදරයක් බැවින් නිකංම i ලෙසද එය ලිවිය හැකිය (29i). මෙලෙසම y අක්ෂය දිගේ පවතින ඒකක දෛශිකය ĵ (“ජේ හැට්”) හෝ j ලෙසද, z අක්ෂය ඔස්සේ පවතින ඒකක දෛශිකය k︢ හෝ k ලෙස ලිවිය හැකිය.

ඇත්තටම ඒකක දෛශික නිරූපණයට i, j, k (හැට් ඇතිව හෝ නැතිව) යොදා ගැනීමම අත්‍යවශ්‍ය නැත. එකිනෙකට වෙනස් සංඛේත 3කුයි යොදා ගැනීමට අවශ්‍ය වන්නේ. එහෙත් විවිධ අය විවිධ සංඛේත යොදා ගන්නට ගියොත් අවුලක් ඇති විය හැකි බැවින් ඉහත ඉංග්‍රිසි අක්ෂර 3 බහුලවම යොදා ගැනේ. ඒ හැරුණහම තවත් සම්මත ආකාර කිහිපයක් තිබෙනවා මෙලෙස කාටිසියානු අක්ෂ ඔස්සේ පවතින ඒකක දෛශික නිරූපණය කිරීම සඳහා. පහත දැක්වෙන්නේ එම නිරූපණ ක්‍රමයි.