සටහන
ටෙන්සරයක
සංරචක සෙට් එක මත අවකලනය සිදු
කළ හැකියි.
එහිදී
විශේෂයෙන් සැලකිය යුතු කරුණු
කිහිපයක් තිබේ.
ඔබ
දන්න සාමාන්ය අවකලන රීතිමයි
තිබෙන්නේ;
නමුත්
ටෙන්සරයක් යනු තනි සංඛ්යාවක්
නොව සංඛ්යා පද්ධතියක් නිසා
සැලකිලිමත් විය යුතුය.
පැහැදිලි
කිරීම සඳහා පලමු ගණයේ ටෙන්සරයක්
ගමු (Ajej).
එකිනෙකට
ප්රලම්භකව පවතින ඒකක/පදනම්
දෛශික 3ක්
ගමු (ත්රිමාන
අවකාශය සඳහා).
ඒ අනුව
Ajej
= A1e1 + A2e2 + A3e3
ලෙස
ටෙන්සරය ප්රසාරණය කළ හැකියිනෙ.
ඇත්තටම
එය අප මීට පෙර ඕනෑ තරම් දැක
තිබෙන ඒකක දෛශික ආශ්රයෙන්
ලියන F
= A1i + A2j + A3k ම
තමයි (මෙම
කාරණයත් සිහියේ තිබීම වැදගත්
වේ).
දැන් ඉහත
ටෙන්සරය (දෛශිකය)
යොදා
ගෙන පහත දැක්වෙන අවකලන අවස්ථාවන්
සලකා බලමු.
ඉහත අවකලනයෙන්
ලැබෙන පිලිතුර 0
වේ.
ඊට
හේතුව විෂය පදය (t)
එම
ගණිත ප්රකාශය තුල කොතැනවත්
විචල්යයක් නොවේ.
යම්
ශ්රිතයක් තුල නොමැති විචල්යයක්
විෂය කරගෙන අවකලනයක් සිදු
කරන විට හැමවිටම පිලිතුර 0
බව ඔබ
අවකලනයේදී ඉගෙන ඇති.
ඉහත (1)
සූත්රයෙන්
කියන්නේ යම් ටෙන්සරයක්
(දෛශිකයක්)
එම
ටෙන්සරය නිරූපණය කරන පදනම්
දෛශික පද්ධතියේ දෙවැනි පදනම්
දෛශිකය විෂයෙන් (පාර්ශ්වික)
අවකලනය
කළ විට අවසාන පිලිතුර ලෙස
ලැබෙන්නේ එම දෙවැනි පදනම්
දෛශිකය ඔස්සේ පවතින ටෙන්සරයේ
සංරචකය බවයි.
මෙම
දෙවැනි පදනම් දෛශිකය e2
ලෙස
හෝ y
ලෙසනෙ
අප ලියන්නේ.
එම
සූත්රය ඕනෑම පදනම් දෛශිකයක්
විෂය කොටගෙන අවකලනය සිදු කරන
විට පොදුවේ ලියන ආකාරය තමයි
(2)
සූත්රයෙන්
දක්වා තිබෙන්නේ (k
දර්ශකයට
1,
2, ආදි
ලෙස ඉලක්කමක් ආදේශ කළ විට (1)
සූත්රයම
ලැබෙනවා).
j දර්ශකය
පමණයි සමාකලනයට යටත් වන්නේ
(එනම්
ඩමි ඉන්ඩෙක්ස් එක වන්නේ).
පහත
දැක්වෙන ගණනය කිරීමත් බැලූ
බැල්මට ඉහත ගණනය කිරීම වැනි
වුවත්,
වෙනසක්
ඇත;
එනම්,
ඉහතදී
k
සමාකලනයට
යටත් නොවුණු අතර,
පහතදී
j
සමාකලන
දර්ශකය වේ.
ඉහත (1)
සූත්රය
පොදු ආකාරය වන අතර,
(2)න්
දක්වා තිබෙන්නේ එය ප්රසාරණය
කර තිබෙන ආකාරයයි (පදනම්
දෛශික 3ක්
ඔස්සේ).
මෙහිදී
j
යන
සමාකලනයට යටත් දර්ශක පදයයි.
පාර්ශ්වික
අවකලනය සිදු කරන විට,
ඒ ඒ
පදනම් දෛශිකය අවකලනය වන්නේ
එම විෂයෙන්මයි.
එනිසා
එම පදනම් දෛශිකවල සංරචක පද
සියල්ල ඉතිරි වේ.
ඉහත දැක්වෙන්නේ
ටෙන්සරයක සම්පූර්ණ අවකලනය
(total
derivative) ලබා
ගන්නා ආකාරයයි.
ඉහත
අවසානයට දක්වා තිබෙන්නේ
ටෙන්සරයේ සම්පූර්ණ අවකලනය
සමාකලන ආකාරයට නිරූපණය කිරීමයි.
ඉහත සූත්රය
පලමු ගණයේ ටෙන්සරයකට අර්ථ
දක්වා ඇත.
එය
දෙවැනි ගනයේ කොන්ට්රවේරියන්ට්
ටෙන්සරයකට අර්ථ දක්වා තිබෙන්නේ
පහත ආකාරයටයි.
මෙහි
i,
j යනු
සමාකලනයට යටත් නොවන පිටතින්
ඉලක්කම් ආදේශ කළ යුතු දර්ශක
පද වේ.
සමාකලනය
සිදු වන්නේ k,
l යන
ඩමී ඉන්ඩෙක්ස් පද දෙක මත පමණි.
ඉහත සූත්ර
දෙක සසඳා බලන විට එහි ඇති
ක්රමවත් රටාව වැටහේවි.
ඒ අනුව
තෙවැනි ගනයේ කොන්ට්රවේරියන්ට්
ටෙන්සරයක් පහත ආකාරයට නිරූපණය
කළ හැකියි නේද?
i, j, k යනු
සමාකලනයට බඳුන් නොවන දර්ශක
පද බව අමුතුවෙන් කිව යුතු
නැහැනෙ.
රටාව තේරුම්ගෙන
ඕනෑම ගණයක් සඳහා සූත්රය
පහසුවෙන්ම සෑදිය හැකිය.
කෝවේරියන්ට්
ටෙන්සර් සඳහාද පරිනාමන න්යායක්
ඇත පහත ආකාරවලට (පිලිවෙලින්
පලමු ගනයේ,
දෙවැනි
ගනයේ,
තෙවැනි
ගනයේ ටෙන්සර් 3
සඳහා
ඒවා පහත දැක්වේ).
මේවායේද
සමාකලනයට බඳුන් නොවන දර්ශක
පද පෙර පරිදිම හඳුනා ගත හැකියි.
ඇත්තටම
=
ලකුණට
වම් පස ඇති පදයේ ඇති දර්ශක පද
තමයි හැමවිටම සමාකලනයට බඳුන්
නොවන්නේ.
එලෙසම දැන්
අපට හැකියි ඕනෑම මිශ්ර
ටෙන්සරයක් සඳහා වූ සූත්ර
ලියන්නටත්.
පහත
දැක්වෙන මිශ්ර ටෙන්සර කිහිපයේ
සූත්ර බලන්න.
පරිනාමන
න්යායක් යොදා ගන්නා අන්දම
උදාහරණයකින් බලමු.
යම්
කෝවේරියන්ට් ටෙන්සරයක (දෛශිකයක)
අනුපිලිවෙලින්
සංරචක xy,
2y-z2, xz වේ.
එම
අගයන් ලබා දී තිබෙන්නේ කාටිසියානු
ඛණ්ඩාංක පද්ධතිය ඇසුරිනි.
එම
දෛශිකයේම කෝවේරියන්ට් සංරචක
දැන් සොයන්න ගෝලීය ඛණ්ඩාංක
පද්ධතිය ඇසුරින්.
මෙය
පලමු ගනයේ කෝවේරියන්ට් ටෙන්සරයක්
නිසා පහත පරිනාමන න්යාය
භාවිතා කළ යුතු වේ (පදනම්
දෛශික 3ක්
සමඟ;
එනම්,
j = 1, 2, 3 වේ).
xj
පද තුන
පහත ආකාරයට (පැරනි)
කාටිසියානු
පද්ධතියේ ඛණ්ඩාංක අක්ෂවලට
අනුරූප වේ.
x1
= x
x2
= y
x3
= z
එලෙසම,
xi පද
තුන පහත ආකාරයට (නව)
ගෝලීය
පද්ධතියේ ඛණ්ඩාංකවලට අනුරූප
වේ.
x1
= r
x2
= θ
x3
= ϕ
තවද,
කාටිසියානු
පද්ධතිය ඇසුරින් සංරචක 3
පහත
ආකාරයට සැලකිය යුතුය.
A1
= xy
A2
= 2y- z2
A3
= xz
අප දන්නවා
කාටිසියානු හා ගෝලීය ඛණ්ඩාංක
අතර පහත ආකාරයට සම්බන්දතා
පවතිනවා (ඛණ්ඩාංක
පාඩම බලන්න).
x
= rsinθcosϕ
y
= rsinθsinϕ
z
= rcosθ
අපට දැන්
ඉහත පරිනාමන න්යාය භාවිතා
කර සෙවීමට තිබෙන්නේ A1,
A2, A3 සංරචක
අගයන් වේ.
ඉහතදී
අවසානයට ලැබි තිබෙන්නේ A1
සංරචකයයි.
නව
ඛණ්ඩාංක පද්ධතිය ගෝලීය නිසා,
ගෝලීය
ඛණ්ඩාංක ඇසුරින් එම සංරචකය
ලැබී තිබේ.
මෙලෙසම
A2,
A3 යන
සංරචක දෙකත් සෙවිය හැකිය.
එම
ගණනය කිරීම් දෙක සිදු කොට
බලන්න.
ටෙන්සර් ගණිත කර්ම
ටෙන්සර් මත
අදිශයකින් ගුණ කිරීම,
එකතු
කිරීම හා අඩු කිරීම,
බහිර්
ගුණිතය (outer
product), අන්තඃගුණිතය
(inner
product), ටෙන්සර්
සංකෝචනය (contraction
of tensor) වැනි
ගණිත කර්ම රාශියක් කළ හැකිය.
මේවා
ගැන කෙටියෙන් විමසමු.
ටෙන්සර් අදිශයකින් ගුණ කිරීම
දෛශිකයක්
අදිශයකින් ගුණ කළ විට සිදු
වූ දේම මෙහිත් සිදු වේ (එහි
අරුමයක් නැත මොකද දෛශිකයක්
යනුත් ටෙන්සරයකි).
එනම්,
ටෙන්සරයේ
විශාලත්වය පමණක් වෙනස් වේ.
තවත්
විදියකින් කියතොත් ටෙන්සරයේ
සංරචක පමණක් ගුණ වේ.
ඕනෑම
ගනයක හා ඕනෑම වර්ගයක ටෙන්සරයක්
සඳහා මෙය පහසුවෙන් සිදු කළ
හැකිය.
දෙවැනි
ගනයේ ටෙන්සරයක් ඇසුරින් එය
බලමු (පදනම්
දෛශික 3ක්
සඳහා).
k යනු
අදිශ අගයකි.
k(Tij)
= kT11,
kT21,
kT31
kT12,
kT22,
kT32
kT13,
kT23,
kT33
ටෙන්සර් එකතු කිරීම හා අඩු කිරීම
එකම ගනයේ
හා එකම වර්ගයේ ටෙන්සර් දෙකක
එකතු කිරීම හෝ අඩු කිරීම කළ
හැකිය.
දෛශිකවල
සිදු කළ ආකාරයටම සිදු වේ.
එනම්,
අනුරූප
සංරචක එකතු හෝ අඩු කරන්න.
උදාහරණයක්
ලෙස Sij
හා Tij
යන
කෝවේරියන්ට් දෙවැනි ගනයේ
ටෙන්සර් දෙක එකතු කරමු.
Sij + Tij
= S11,
S21,
S31
T11,
T21,
T31
S12,
S22, S32
+ T12,
T22, T32
S13,
S23, S33
T13,
T23, T33
=
S11+
T11
, S21+
T21
, S31+
T31
S12+
T12
, S22+
T22
, S32+
T32
S13+
T13
, S23+
T23
, S33+
T33
ඉහත ආකලනය
පහත ආකාරයටද නිරූපණය කළ හැකිය.
ටෙන්සර්
එකතු කිරීමේදී හා අඩු කිරීමේදී
අවසානයේ ලැබෙන පිලිතුරේ ගනය
හා වර්ගය එකතු කිරීමට හෝ අඩු
කිරීමට භාජනය වූ ටෙන්සර් දෙකේ
ගනය හා වර්ගයට සමාන වේ.
එනිසයි
පහත Rij
යනුවෙන්
පිලිතුර ලෙස ලැබුණු අවසන්
ටෙන්සරය නම් කර තිබෙන්නේ.
ටෙන්සර් බහිර්ගුණිතය
ඍජු ගුණිතය
(tensor
direct product) ලෙසද
මෙය හැඳින්වේ.
යම්
ටෙන්සරයක් තවත් ටෙන්සරයක්
සමඟ බහිර්ගුණිතය සිදු කරන
විට, පහත
ආකාරයට එය සිදු වේවි.
උදාහරණය
සඳහා යොදා ගෙන ඇත්තේ දෙවැනි
ගනයේ කෝවේරියන්ට් ටෙන්සරයක්
හා දෙවැනි ගනයේ කොන්ට්රවේරියන්ට්
ටෙන්සරයකි.
එහෙත්
මේ සඳහා ටෙන්සර් දෙකෙහි ගනය
හා වර්ගය සමාන වීම අත්යවශ්ය
නොවේ.
අවසාන
වශයෙන් ලැබෙන පිලිතුරු ටෙන්සරයේ
ගනය හැමවිටම ගුණිතයට බදුන්
වන ටෙන්සර් දෙකෙහි ගනයන්වල
එකතුවට සමාන වන අතර,
ටෙන්සර්
වර්ගයද ගුණිතයට හවුල් වන
ටෙන්සර් දෙකෙහි වර්ගයන්වල
මිශ්රණයකි.
ටෙන්සර්
දෙකෙහි යොදන උඩකුරු/යටකුරු
හැමවිටම වෙනස් අක්ෂර භාවිතා
කරන්න (එනම්,
එක්
ටෙන්සරයකට භාවිතා කළ අකුරු
අනෙකෙහි නොයොදන්න).
සටහන
මීට පෙර
ක්රොනික ඩෙල්ටා සංකල්පය අප
ඉගෙන ගත්තා මතකද?
එය පහත
ආකාරයටත් අර්ථ දැක්විය හැකිය
(කෝවේරියන්ට්
හා කොන්ට්රවේරියන්ට් දර්ශක
යොදා ගෙන).
ටෙන්සර් සංකෝචනය
මෙහිදී යම්
මිශ්ර ටෙන්සරයක ගනය 2කින්
අඩු කෙරේ (එනම්
ගනය සංකෝචනය වේ).
එය කළ
හැක්කේ මිශ්ර ටෙන්සරයේ ඇති
කෝවේරියන්ට් දර්ශකයක් එම
මිශ්ර ටෙන්සරයේම ඇති
කොන්ට්රවේරියන්ට් දර්ශක
පදයකට සමාන කිරීමෙනි.
උදාහරණයකින්
එය බලමු (පහත
සුලු කිරීම බලන්න).
මෙහිදී
l යන
කෝවේරියන්ට් දර්ශකය සමාන
කරනවා i
යන
කොන්ට්රවේරියන්ට් දර්ශකයට.
අවශ්ය
නම් i නැතිව,
j, k යන දර්ශක
පද දෙකෙන් එකකට වුවද එය සමාන
කළ හැකිය.
එහෙත්
සමාන කරන්නට භාවිතා කරන දර්ශක
පදය වෙනස් වන විට අවසානයේ
ලැබෙන පිලිතුර (ටෙන්සරය)
වෙනස්
වේ. උදාහරණයක්
ලෙස, Aijki
හා Aijkk
යනු එකිනෙකට
වෙනස් ටෙන්සර දෙකකි (සංකෝචනයෙන්
පසුව).
අවසානයේ
පාර්ශ්වික අවකලන දෙකකින්
යුතු ප්රකාශයක් ලැබී තිබෙන
නිසා, එය
දෙවැනි ගනයේ ටෙන්සරයක් බව
පෙනේ.
සංකෝචනය
සිදු කිරීමට පෙර එය හතරවැනි
ගනයේ ටෙන්සරයක් විය.
ටෙන්සර් අන්තඃගුණිතය
මෙය ටෙන්සර්
තිත් ගුණිතය (tensor
dot product) ලෙසත්
හැඳින්විය හැකිය.
මෙහිදී
දෙන ලද ටෙන්සර් දෙකක බහිර්ගුණිතය
පළමුව සිදු කර,
ඉන් සෑදෙන
ටෙන්සරය මත ටෙන්සර් සංකෝචනය
සිදු කළ යුතුය (බහිර්ගුණිතයට
සහභාගී වූ ටෙන්සර් දෙකෙන්
උඩකුරක් හා යටකුරක් එකිනෙකට
සමාන කළ යුතුය).
මෙය සිදු
වීමට නම්,
බහිර්ගුණිතය
සිදු වීමෙන් පසු අනිවාර්යෙන්ම
මිශ්ර ටෙන්සරයක් ලැබිය යුතුය
(ඒ
කියන්නේ බහිර්ගුණිතයට සහභාගි
වන ටෙන්සර් දෙකෙන් එකක් හෝ
මිශ්ර ටෙන්සරයක් විය යුතුය
නැතහොත් එම ටෙන්සර් දෙකේ වර්ගය
වෙනස් විය යුතුය).
ටෙන්සර්
සංකෝචනයක් තිබෙන නිසා,
අන්තඃගුණිතයේදී
ගුණිතයට සහභාගිවන ටෙන්සර්
දෙකේ ගනයන් දෙකේ එකතුවට 2ක්
අඩු ගනයක් ලැබේවි.
උදාහරණයකින්
මෙය බලමු.
ඔබ දෛශිකවල
දුටු තිත් ගුණිතයත් මෙම
අන්තඃගුණිතය තමයි.
දෛශික
දෙකක් බහිර්ගුණිතය සිදු කරන
විට පිලිතුරේ ගනය 2ක්
වෙනවානෙ.
ඉන්පසු
සංකෝචනය සිදු කරන විට,
ගනය 2කින්
අඩු වෙනවානෙ.
මෙනිසා
අවසාන පිලිතුරේ ගනය ශූන්ය
වේ. ඉතිං
දෛශික දෙකක තිත් ගුණිතයෙන්
ලැබෙන්නේ අදිශයක් නේද?
ගණිතයේ බොහෝ (සමහරවිට සියලුම) සංකල්ප දෙයාකාරයකින් තේරුම් ගැනීමට හැකිය. එකක් නම්, භෞතික ලෝකයේ අපට සංජානනය වන (අපේ පංචේන්ද්රියන්ට හෝ උපකරණවලට දැනෙන) යම් යම් සිද්ධි (මේවා භෞතික සංසිද්ධි ලෙස හැඳින්වේ) නිරූපණය කිරීමට ගණිත සංකල්ප භාවිතා වේ. එහි පුදුමයක්ද නැත මොකද ගණිතය යනු විද්යාවේ භාෂාවයි. උදාහරණයක් ලෙස, භෞතික ලෝකයේ තිබෙන ස්කන්ධය, ඝනත්වය වැනි දෑ මැනීමේදී හා ඒවා සමඟ කටයුතු කිරීමේදී ගණිතය පැත්තෙන් ඊට අදිශ රාශි කියා සංකල්පයක් හඳුන්වා දේ. එලෙසමයි දෛශික ගැනත්. භෞතික ලෝකයේදී බලය, ත්වරණය ආදී රාශිවලට විශාලත්වයක් හා දිශාවක් නිශ්චිතව පවතී. ගණිතයේදී ඒවා දෛශික යන සංකල්පය යටතේ සලකා බැලේ.
එහෙත් ගණිතය
දෙවැනි ආකාරයට තේරුම්ගැනීම
පළමු ආකාරයට වඩා තරමක් අපහසුය.
ඇත්තටම
තරමක් නොව,
ඉතාම
අපහසු මට්ටමක් දක්වා එය විහිදී
යා හැකිය.
ඊට හේතුව
මෙහිදී නිදහස උපරිම වේ.
භෞතික
සංසිද්ධි සමඟ දැන් ගණිතය
ගැටගැසෙන්නේ නැත.
එනිසා
ඔබ මෙම දෙවැනි ආකාරයෙන් යමක්
ගණිතයෙන් පැවසුවොත්,
ඒ කියන
දෙය භෞතික ලෝකයේ මෙහෙමයි කියා
පෙන්වා දීමට අවශ්ය නැත.
මෙහිදී
කරන්නේ එම සංකල්පය හඳුන්වාදෙන
හා එය දියුණු කරන ගණිතඥයන්
යම් යම් කොන්දේසි හා රීති
සමුදායක් (එම
කොන්දේ හා රීති ඇත්තටම තාර්කික
වේ) ඉදිරිපත්
කිරීමයි.
ඒ අනුව දෛශික
හා ටෙන්සර්ද ඉහත දෙයාකාරයෙන්ම
තේරුම්ගත හැකියි.
මෙහි මා
උත්සහ කළේ ටෙන්සර් ගැන මූලික
දැනුමක් ලබා දීමටයි.


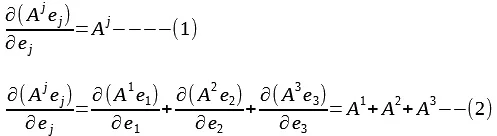



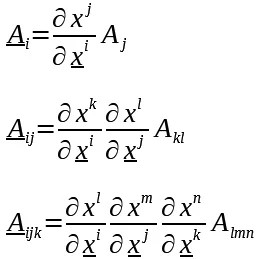








මේ සටහන් කිසිත් මට නොවැටහෙන්නේ මෙය මගේ විෂය නොවන බැවිනි. නමුත් මා ඔබ අගය කරන්නේ මෙය මේ විෂයට අත්පොත් තබනා සියල්ලන්ටම මහානර්ඝ ලිපි පෙළක් බැවිනි.
ReplyDelete:) ස්තූතියි එරන්දි...මං හිතන්නේ ටෙන්සර් ගැන සිංහලයෙන් සංක්ෂිප්තව හෝ ලියා ඇති ලිපි/පාඩම් කිහිපය මෙයයි. ශතවර්ශ ගණන් පැරණි මෙවන් දැනුම ගැන ඊනියා උගතුන් මෙතෙක් වචනයකුදු නොලියා සිටීම ඉගෙනීමට පිපාසයෙන් සිටින ලාංකිකයන්ගේ අභාග්යයකි.
Delete