සටහන
ඔබ
දන්නවා සාමාන්යයෙන් අප
ශ්රිතයක් දක්වන්නේ f(x),
g(x,y), y වැනි
සංඛේත ක්රමයකින්.
නිකංම
y
හෝ
z
හෝ
ලෙස අක්ෂරයකින් ශ්රිතයක්
නිරූපණය කළ හැකි වුවත් f(x,y)
හෝ
g(t)
වැනි
ක්රමය වඩා හොඳ වන්නේ එහිදී
ශ්රිතයේ තිබෙන ස්වායත්ත
විචල්යයන්ද ශ්රිතයේ නාමයේ
වරහන තුල පවතින නිසාය.
එනිසා
z
= 2x4
+ 5y හා
f(x,y)
= 2x4
+ 5y යන
දෙකෙන්ම එකම ශ්රිතය නිරූපනය
කළත්,
දෙවැනි
නිරූපන ක්රමය වඩා හොඳයි.
යම්
දෛශික ශ්රිතයක් ඒකක දෛශික
ආශ්රයෙන් නිරූපනය කරන හැටි
ඔබ දන්නවා.
උදාහරණයක්
ලෙස,
f(x,y,z)
= 3xy i
-
5y2
j + xz k යන
දෛශික ශ්රිතය ගන්න.
මෙම
ශ්රිතයම f(x,y,z)
= (3xy, 5y2,
xy) ලෙසද
සමහරුන් දක්වනවා (හරියට
ඛණ්ඩාංක අගයක් දක්වන්නා සේ).
මෙවිට
පහත ආකාරයටද අවකලනයෙන් (අනුකලන
හෝ වෙනත් ගණිත කර්ම වුවද)
පසුව
ලැබෙන ශ්රිත දැක්විය හැකියි.
ඒ
කියන්නේ,
f(x,y,z) = x2yi
+ sin(x)j + xzk යන
දෛශික ශ්රිතය අවකලනය කළ විට,
2xyi + cos(x)j + zk යන
ශ්රිතය ලැබෙන බවයි.
ඉහත
පෘෂ්ට
අනුකල දක්වන සූත්ර
හුරුබුහුටි වුවත්,
සුලු
කරන විට තරමක් සංකීර්ණ
ස්වභාවයක් ගනී.
ශ්රිතය
ඒකක දෛශික ආශ්රයෙන් (එනම්,
f(x,y,z) = Pi + Qj + Rk
ස්වරූපයෙන්)
අප
දන්නවා (එය
දන්නා දත්තයක්).
දැන්
අපට අවශ්ය වෙනවා ඒකක
අභිලම්භක
දෛශිකය (N)
දැනගන්නට.
එය
සාමාන්යයෙන් දත්තයක් ලෙස
ලබා නොදී තිබිය හැකියි.
එවිට,
එය
අප සකස් කර ගත යුතුය.
එය
එකවරම තීරණය කළ හැකියි පෘෂ්ටය
තිරස් හෝ සිරස් තලයක් ලෙස පවතී
නම්.
එනම්,
ත්රිමාන
ඛණ්ඩාංක පද්ධතියක,
x-y, x-z, y-z ලෙස
එකිනෙකට ලම්භක තල 3ක්
තිබෙනවානෙ.
ඉතිං,
අප
සලකා බලන පෘෂ්ටයක්ද මෙවැනි
තලයක් මත හෝ ඊට සමාන්තරව
පිහිටියේ නම්,
අභිලම්භකය
වන්නේ තලය සෑදීමට හවුල් නොවූ
අනෙක් අක්ෂයේ දිශාවයි.
උදාහරණයක්
ලෙස,
x-y තලයේ
අභිලම්භකය පිහිටන්නේ z
අක්ෂය
ඔස්සේය.
එලෙසම,
x-z තලයේ
අභිලම්භකය y
අක්ෂය
ඔස්සේද,
y-z තලයේ
අභිලම්භකය x
අක්ෂය
ඔස්සේද පිහිටයි.
දම්පාටින්
දක්වා තිබෙන්නේ තල 3ට
ඇඳි අභිලම්බ 3යි
(එම
ඊහිස් අනෙක් පසට සිටින සේද
අභිලම්බක ඇඳිය හැකියි).
එහෙත්
පෘෂ්ටය එවැනි තිරස් හෝ සිරස්
තලයක් නොවන විට (එනම්,
ආනත
තලයක් හෝ වක්ර පෘෂ්ටයක් වන
විට),
එය
සොයන ආකාරයක්ද ඇත.
ඒ
සඳහා පළමුව
ග්රැඩ් කර්මය සිදු කරන්න
පෘෂ්ටය නිරූපණය කරන ශ්රිතය
මත.
එවිට
ලැබෙන්නේ ඒ පෘෂ්ටයේ අභිලම්භයයි.
එහෙත්
එය ඒකක අභිලම්භකයක් බවට පත්
කිරීමට,
ග්රැඩ්
කර්මයෙන් ලැබුණු ප්රතිපලයේ
විශාලත්වයෙන් බෙදිය යුතුය
(ඒකක
දෛශික පාඩමේදී මේ ගැන අප කතා
කළා).
එවිට
අවසන් සම්පූර්න සූත්රය පහත
ආකාරයට විය යුතුයි.
උදාහරණයක්
බලමු. x2+y4+3yz=2
මඟින්
යම් පෘෂ්ටයක් නිරූපණය කරනවා
යැයි සිතමු. මෙම
පෘෂ්ටය සඳහා ඒකක අභිලම්භකය
සොයමු. මෙය
f(x,y,z) = x2+y4+3yz - 2
= 0 ලෙස
ලිවිය හැකියි. මෙම
ශ්රිතය මත ඉහත විස්තර
කළ පරිදි ඒකක අභිලම්බකය සොයන
පියවර දෙක අනුගමනය කරමු.
ඉහත
පෘෂ්ටයේ (1,2,1)
යන
ලක්ෂ්යයේදී ඒකක අභිලම්භකයේ
අගය දැන් සොයමු.
මෙම
ඛණ්ඩාංක අගයන් ඉහත ප්රතිපලයට
ආදේශ කරන්න.
ඇත්තටම
තිරස් හෝ සිරස් තලයක් සඳහා
වූ අභිලම්භකය (හෝ
ඒකක අභිලම්බකය)
සෙවීමටද
ඉහත ග්රැඩ් ගණිත කර්මය එසේම
යොදා ගත හැකියි.
උදාහරණයක්
ලෙස,
ත්රිමාන
ඛණ්ඩාංක පද්ධතියක z
= 5 යන
තලයට පවතින අභිලම්භකය සොයමු.
ඒ
කියන්නේ මෙම තලයේ ශ්රිතය
f(x,y,z)
= z
ලෙස
පොදුවේ ලිවිය හැකිය.
තවද,
බොහෝවිට
පෘෂ්ටය කොටස් වශයෙන් සුමට
පෘෂ්ට වේ.
එවිට,
සමස්ථ
පෘෂ්ටය එකවර අනුකලය නොකර,
කොටස්වල
අනුකල වෙන වෙනම සොයා ඒවා එකතු
කළ හැකියි.
උදාහරණයක්
ලෙස, කොටස්
වශයෙන් සුමට යම් පෘෂ්ටයක කොටස්
3ක්
තිබෙන්නේ නම්,
පහත ආකාරයට
ලිවිය හැකියි.
එහි S1,
S2, S3 ආදි
වශයෙන් සංඛේතවත් කරන්නේ පෘෂ්ට
කොටස් 3යි.
පෙරත් සඳහන්
කළ ලෙසටම,
පෘෂ්ට
අනුකලනය පහත ආකාරයේ පුනර්කෘත
අනුකලයක් බවට පත් කර ගත යුතුයි
එය සුලු කිරීමට නම්.
ඇත්තෙන්ම
මෙය අනුකලනයට අදාල කරුණක්
මිස දෛශිකවලට අදාල කරුණක්
නොවේ. dS
යනු ඉතා
කුඩා වර්ගපලයක් නිසා,
එය පුනර්කෘත
අනුකලනයකට පරිවර්තනය කරන
විට, ලැබෙන
dq, dt යන
විෂය පදද නියෝජනය කරන්නේ අවසාන
වශයෙන් දිගවල් දෙකකි (ඔබ
දන්නවා දිගවල් දෙකක් හෙවත්
දිගක් පළලක් එකිනෙකට ගුණ කළ
විට වර්ගපලයක්නෙ ලැබෙන්නේ).
පෘෂ්ටය
යම් තලයක් නම් (එනම්
වක්රතාවක් නැත),
උදාහරණයක්
ලෙස, x-y
තලයක්
මත dS යන්න
dxdy ලෙස
සකස් වේ (dS
= dxdy). එහෙත්
පෘෂ්ටය වක්රයි නම්,
නිකංම
dxdy ලෙස
ලිවිය නොහැකිය (වක්රතාව
පෙන්නුම් කරන අමතර ගුණිත
කොටසක් අවශ්ය වේවි dS
= (3/x)dxdy වැනි).
දැන් අප
උදාහරණයක් බලමු.
දෛශික
ක්ෂේත්ර ශ්රිතය F
= 2x2yi - y2j + 4xz2k වේ.
ත්රිමාන
ඛණ්ඩාංක පද්ධතියක පළමු අෂ්ටමකයේ
(octant) සීමා
වී තිබෙන සිලින්ඩරය y2
+ z2 = 9 මඟින්
නිරූපණය වේ.
එම සිලින්ඩරය
x = 0, x = 2, y =
0, z = 0 යන
තල මඟින් සීමා වී තිබේ.
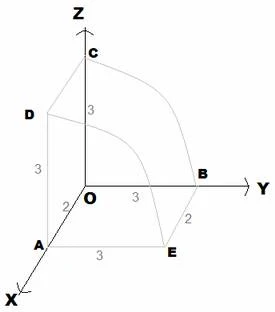
පහත රූපයෙන්
දැක්වෙන්නේ එම විස්තරයයි.
මෙහි සමස්ථ
මතුපිට සෑදි තිබෙන්නේ කොටස්
5කින්ය.
එම කොටස්
5 පහත
ආකාරයට පවතින බව පෙනේ.
ඒ කියන්නේ
මෙය කොටස් වශයෙන් සුමට පෘෂ්ටයකි.
s1 = AEBO (x-y තලයකි)
s2 = AOCD (x-z
තලයකි)
s3 = BOC (y-z තලයකි)
s3 = BOC (y-z තලයකි)
s4 = AED (y-z තලයකි)
s5 = EBCD (වක්ර
තලයකි)
දැන් මෙම
මුලු පෘෂ්ට අනුකලය කොටස්වල
පෘෂ්ට අනුකලවල එකතුවට සමාන
කළ හැකිය.
s1 කොටසේ
පෘෂ්ට අනුකලනය සොයමු.
මෙම පෘෂ්ට
කොටසේ ඒකක අභිලම්භකය වන්නේ
k වේ.
අමුතුවෙන්
එය සොය සොය ඉන්නට අවශ්ය නැහැනෙ;
තිරස්
පෘෂ්ටයක් ගත් විට එහි අභිලම්භකය
සිරස් වේ.
තවද,
මෙම පෘෂ්ටයේ
ඕනෑම ලක්ෂ්යයක z
අගය 0
වේ (දී
තිබෙන දත්තයක්).
දැන් අපි
s2
කොටසේ
පෘෂ්ට අනුකලනය සොයමු.
මෙම කොටසේ
ඒකක අභිලම්භකයත j
බව බැලූ
ගමන්ම පෙනේ.
තවද මෙම
පෘෂ්ටයේ ඕනෑම ලක්ෂ්යයක y
අගය 0
වේ (දී
තිබෙන දත්තයක්).
දැන් අපි
s3
කොටසේ
පෘෂ්ට අනුකලනය සොයමු.
මෙම කොටස්
ඒකක අභිලම්භකය i
බව එකවරම
තේරුම් ගත හැකියි.
මෙම පෘෂ්ටයේ
ඕනෑම ලක්ෂ්යයක x
අගය 0
වේ (දී
තිබෙන දත්තයක්).
s4 කොටසේ
පෘෂ්ට අනුකලනය දැන් සොයමු.
මෙහිද
ඒකක අභිලම්බකය i
වන අතර,
මෙම පෘෂ්ටය
මත ඕනෑම ලක්ෂ්යයක x
අගය 2
වේ.
ඉහත අවස්ථා
3දිම
පුනර්කෘත අනුකලනය කිරීමේ
අවශ්යතාව මතු වූයේ නැහැ මොකද
අනුකලනය කෙරෙන ශ්රිත කොටස
ශූන්ය වූවා.
එහෙත්
දැන් එය ශූන්ය නොවන නිසා,
පුනර්කෘත
අනුකලනය යොදා ගැනීමට සිදු
වේ. මෙම
පෘෂ්ටයත් තලයකි.
එනිසා
dS = dydz වන
අතර, x
විචල්යයද
නියත පදයක් බවට පත් වෙනවා මොකද
එම විචල්යයේ අගය මෙම තලය මතදී
නියත වේ.
dy විෂය
පදයට සාපේක්ෂව අනුකල සීමා
වන්නේ 0
සිට √(9
- z2) වේ.
dz විෂය
පදයට සාපේක්ෂව අනුකල සීමා
වන්නේ 0
සිට
3 දක්වා
වේ.
අවසාන වශයෙන්
s5
කොටසේ
පෘෂ්ට අනුකලය සිදු කළ යුතුය.
එය පෙර
අවස්ථා 4ටම
වඩා සංකීර්ණ වේ.
පළමුව
එහි ඒකක අභිලම්භකය සෙවිය
යුතුය.
y2 + z2 = 9 = 32 යන
දත්තයද සුලු කිරීමේදී යොදා
ගෙන තිබේ.
මෙම වක්ර
පෘෂ්ටය සඳහා dS
= (3/z)dxdy වේ.
ශ්රිතය
හා ඉහත ඒකක අභිලම්භකය යන දෙකෙහි
තිත් ගුණිතය අනුකලනය තුල ලබා
ගෙන, ඉන්පසු
එය පුනර්කෘත අනුකලනයෙන් සුලු
කරන්න.
පුනර්කෘත
අනුකලනයේදී සුලු කිරීමේ පහසුව
තකා විචල්ය ආදේශයක් සිදු කර
තිබේ (අනුකලන
ගණන් සෑදීමේ උපක්රමයකි එය).
y-z තලයේ
පවතින වෘත්තයක් නිසා (y2
+ z2 = 9 නිසා),
සයින්
හා කොස් ආශ්රයෙන් y,
z දක්වා
තිබෙන ආකාරය නිවැරදි බව ඔබට
වැටහිය යුතුය.
එනම්,
අරය ඒකක
3ක්
දිග වන වෘත්තයක,
එම වෘත්ත
පරිධියේ ඕනෑම ලක්ෂ්යයක්
විසින් අක්ෂ දෙක මත ප්රක්ෂේපිත
දිගවල් 3cos(t)
හා 3sin(t)
වේ (t
යනු
කෝණයයි).
පුනර්කෘත
අනුකලය තුල x
විෂයට
අදාල අනුකල සීමා දෙක වනුයේ 0
සිට 2
දක්වාය
(දී
තිබෙන දත්තයකි).
අනෙක්
අනුකලය කෝණයක් ඇසුරින් තිබෙන
නිසා, එහි
සීමා අගයන් දෙක විය යුත්තේ 0
සිට අංශක
90 දක්වාය.
එයද දී
තිබෙන දත්තයක් ඇසුරින්
වක්රාකාරයෙන් ලබා ගත් දත්තයකි
මොකද වෘත්ත කොටස පවතින්නේ
අංශක 90ක
කොටසක් තුල පමණි (මුලින්
පෙන්වා දුන් රූපය බලන්න).
දැන්,
පෘෂ්ට
කොටස් සියල්ලේම වෙන වෙනම අනුකල
අගයන් ලැබී ඇත.
අවසාන
පිලිතුර වන්නේ එම අගයන් සියල්ලේම
එකතුවයි.
ඇත්තෙන්ම
අනුකලයක් සුලු කිරීමට ආකාර
කිහිපයක්ම තිබිය හැකිය.
ඒ කියන්නේ
දෛශික පිලිබඳ කාරණයක් නොවේ
සුලු කිරීම.
එනිසා
ඉහත ගැටලුව වෙනත් ආකාරවලින්ද
සුලු කළ හැකි වේවි.
මෙතෙක්
විස්තරය හා උදාහරණද සලකා
බැලුවේ අනුකලය තුල තිත් ගුණිතය
තිබෙන ආකාරයේ පෘෂ්ට අනුකලය
ගැනයි.
භෞතික
විද්යාවේදි බහුලවම අවශ්ය
වන ස්වරූපයද එයයි.
විද්යුත්,
චුම්භක,
ගුරුත්ව
ආදී ක්ෂේත්ර තුල යම් කාර්යන්
සිදු කරන විට,
ඇත්තටම
මෙම පෘෂ්ට අනුකල ගණිත කර්මය
තමයි එතැන යෙදෙන්නේ.
එවිට,
අදාල
දෛශික ශ්රිතයෙන් නිරූපණය
කෙරෙන්නේ ක්ෂේත්රය වේ.
එනිසා
ස්රාව ආකෘති (flux
model) නිතරම
මෙම පෘෂ්ට අනුකල ක්රමයෙන්
ඉදිරිපත් කෙරේ.
අනෙක්
පෘෂ්ට අනුකල ආකාර දෙකද ඒ
ආශ්රයෙන් තේරුම් ගත හැකිය.
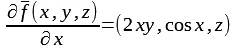







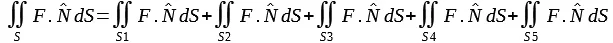







Comments
Post a Comment
Thanks for the comment made on blog.tekcroach.top