දෛශික (vectors) - 2

පහත දැක්වෙන්නේ කාටිසියානු පද්ධතියේ අක්ෂ ඔස්සේ නිර්වචනය කර ගත් ඒකක දෛශික ඇසුරින් දෛශික ලියා දක්වා තිබෙන උදාහරණ කිහිපයකි.

දෛශිකයේ දිශාව අනුව සංරචක තුනෙන් දෙකක් හෝ එකක් පමණක් වුවද තිබිය හැකියි (සංරචක තුනම තිබීම අත්‍යවශ්‍ය නැත). යම් සංරචකයක් ශූන්‍ය යැයි කියන්නේ එම දිශාව ඔස්සේ දෛශිකයේ අගයක් නොමැති බවයි. ඉහත උදාහරණ දුටු විට ඔබට පෙනෙනු ඇති ඕනෑම මාන ගණනක් සහිත දෛශිකයක් පහසුවෙන්ම ලිවිය හැකි බව (ඉහල මාන ඇඳිය හෝ සිතින් මවා ගත නොහැකි වුවත්). ක්වන්ටම් භෞතිකයේදී මාන ඕනෑම ගණනක් (අනන්ත ගණනක්) සඳහා වූ දෛශික භාවිතා කෙරෙනවා (එනම්, හිල්බර්ට් අවකාශය ක්වන්ටම් භෞතිකය තුල භාවිතා වේ).

a = 3i (1 dimensional)

b = 2i + 3j (2 dimensional)

c = 9i + j + 3k (3 dimensional)
d = 2i + 4j + 8k + 3l (4 dimensional)

f = 4i - j + 2k - 4l + 6m (5 dimensional)

වැඩි වන සෑම මානයක් සඳහාම අලුතින් පදයක් (ඒකක දෛශිකයක්) ඇතුලත් කිරීමට පමණයි තිබෙන්නේ. මෙලෙස ඉහලට මාන වැඩි වන විට, i, j, k නිරූපණ ක්‍රමය සීමාසහිත වේ (මොකද ඉංග්‍රිසි අකුරු තිබෙන්නේ ටිකකි). මෙවිට තමයි e₁, e₂, e₃ ආදි හෝ x₁, x₂, x₃ ආදි නිරූපණ ක්‍රමයන් වැදගත් වන්නේ.

ඔබ දන්නවා දෛශිකයක් අවකාශයේ යම් දිශාවක් ඔස්සේනෙ පවතින්නේ. එම තනි දෛශිකයම යම් ඛණ්ඩාංක පද්ධතියක් තුල නිරූපණය කළ හැකි බවද ඔබ දැන් දන්නවා. ඉහත පෙන්නුවා දෛශික කිහිපයක්ම ඛණ්ඩාංක පද්ධතියක් ඇසුරින් ලියා දක්වන අයුරු. පහත රූපයේ දැක්වෙන්නේ රූපමය වශයෙන් දෛශිකයක් ඛණ්ඩාංක පද්ධතියක ඇඳ දක්වන අයුරුයි (ත්‍රිමාන හා ද්විමාන අවකාශයක පමනයි රූපමය වශයෙන් අප දක්වන්නේ).

ඉහත රූපය බලන විට පෙනී යනවා එම තනි දෛශිකයම ඛණ්ඩාංක පද්ධතියේ අක්ෂ ඔස්සේ පවතින කොටස් හෙවත් සංරචක වශයෙන් සකස් කර, එම එක් එක් සංරචකය ඒකක දෛශික ආශ්‍රයෙන් දක්විය හැකි බව. යම් දෛශිකයක් එහි සංරචකවලට කඩා නිරූපණය කිරීම "දෛශික විභේදනය" (resolution of vectors) ලෙස හැඳින්වෙනවා.

දිශා කෝසයින

දෛශිකයක් විභේදනය කිරීම ඉතාම පහසු අතර, ඒ සඳහා සරල ත්‍රිකෝණමිතිය යොදා ගැනේ. පහත රූපය බලන්න. එහි t නම් දෛශිකයක් ඇඳ තිබේ. එහි විශාලත්වය ||t|| ලෙස දක්වා තිබේ. එම දෛශිකයක නිරූපණය කරන ඍජු රේඛා ඛණ්ඩය හා x අක්ෂය අතර කෝණය α ලෙසද සටහන් කර ඇත. දැන් දෛශිකය නිරූපණය කරන රේඛා ඛණ්ඩය විසින් x අක්ෂය මත සිදු කරන ප්‍රක්ෂේපණය (projection) t(cos α) වේ. එම ප්‍රක්ෂේපිත අගය තමයි x අක්ෂයේ දිශාව ඔස්සේ එම දෛශිකයේ සංරචකයේ විශාලත්වය.

මෙලෙසම, y අක්ෂය හා z අක්ෂය සමඟද එම t දෛශිකය β හා γ යන කෝණ දෙක පිළිවෙලින් සාදයි. ඒ අනුව, y අක්ෂය මත දෛශිකයේ ප්‍රක්ෂේපණය හෙවත් එම අක්ෂය ඔස්සේ දෛශිකයේ සංරචක අගය t(cos β) වන අතර, z අක්ෂය මත දෛශිකයේ ප්‍රක්ෂේපණය හෙවත් එම අක්ෂය ඔස්සේ දෛශිකයේ සංරචක අගය t(cos γ) වේ.

යම් දෛශිකයක් කාටිසියානු ඛණ්ඩාංක පද්ධතියක අක්ෂ ඔස්සේ විභේදනය කිරීමේදී ඉහත කෝණ දැන සිටීම අත්‍යවශ්‍ය වේ. ඇත්තටම එම කෝණවල කෝසයිනයයි යොදා ගන්නේ. එනිසා, මෙම කෝණවල කෝසයින අගයන් “දිශා කෝසයින” (direction cosines) ලෙස නම් කෙරෙනවා. x අක්ෂයට අදාල දිශා කෝසයිනය l අක්ෂරයෙන්ද, y අක්ෂයට අදාල දිශා කෝසයිනය m අක්ෂරයෙන්ද, z අක්ෂයට අදාල දිශා කෝසයිනය n අක්ෂරයෙන්ද නිරූපණය කෙරෙනවා. ඒ අනුව, යම් දෛශිකයක් කාටිසියානු ඛණ්ඩාංක පද්ධතිය තුල නිරූපණය කිරීමට දිශා කෝසයින අවශ්‍ය වෙනවා. එවිට පහත ආකාරයට සුලු කිරීම සිදු කළ හැකියි.

බොහෝ තැන්වල ඇත්තටම ඉහත අවසාන ස්වරූපයේ ආකාරයෙන් නොවෙයි එය දක්වා තිබෙන්නේ. ඊට හේතුව, ඒවායේදී ඉහත ප්‍රකාශය තවත් සරල කිරීම සඳහා t දෛශිකය ඒකක දෛශිකයක් ලෙසයි ගෙන තිබෙන්නේ. එවිට එහි විශාලත්වය හෙවත් ||t|| 1 බවට පත් වේ. එවිට පහත ආකාරයට එම ප්‍රකාශය සරල වේ.

 

යම් දෛශිකයක් i, j, k යන ඒකක දෛශික මඟින් නිරූපණය කර ඇති විටක, එම දෛශිකයේ විශාලත්වය සොයන්නේ කෙසේද? එය හරිම සරලයි. i හා j පමණක් ඇති ද්විමාන දෛශිකයකදී පයිතගරස් ප්‍රමේයය භාවිතා කළ යුතුය. එහිදී සංරචක දෙකෙහි විශාලත්ව අගයන් ඍජුකෝණි ත්‍රිකෝණයේ කර්ණය නොවන පාද දෙක ලෙස සලකා ප්‍රමේය යොදන්න. උදාහරණයක් ලෙස, a = 2i + 3j යන ද්විමාන දෛශිකයේ විශාලත්වය වන්නේ:

|a|² = 2² + 3² = 13

|a| = √13

දෛශිකයේ මාන ගණන වැඩි වන විට, පයිතගරස් ප්‍රමේයේ ආකාරයටම (එම රටාවටම) ගණනය කිරීම සිදු කළ යුතුය. උදාහරණයක් ලෙස, a = 2i + 3j + 4k යන ත්‍රිමාන දෛශිකයේ විශාලත්වය වන්නේ:

|a|² = 2² + 3² + 4² = 29

|a| = √29

දෛශික මත ගණිත කර්ම

දෛශික මත ගණිත කර්ම රාශියක් සිදු කළ හැකිය. යම් දෛශිකයක් ඛණ්ඩාංක පද්ධතියක් ආශ්‍රයෙන් නිරූපණය කරන විටත්, ඉහතදී ඔබ දුටු ආකාරයට යම් යම් ගණිතමය සුලු කිරීම් යොදා ගැනීමට සිදු වුවත්, ඒවා දෛශික මත සිදු කරන ගණිත කර්ම නොවන බවද සිහි තබා ගන්න.

යම් දෛශික දෙකක් එකම විශාලත්වයෙන් හා එකම දිශාවට යොමුව ඇත්නම්, එම දෛශික දෙක සමාන වේ. එහෙත් එහි කොන්දේසියක් ඇත. එනම්, එම දෛශික දෙකම එකම රාශියක් ගැන විය යුතුය. උදාහරණයක් ලෙස, එක් දෛශිකයක් ප්‍රවේගයක්ද අනෙක් දෛශිකය බලයක්ද හඟවයි නම්, එම දෛශික දෙකෙහි සංඛ්‍යාත්මක අගයන් හා දිශා සමාන වුවත්, එම දෛශික දෙක සමාන විය නොහැකියිනෙ (කොහොමද ඇපල් ගෙඩියක් දොඩම් ගෙඩියකට සමාන වන්නේ?).

තවද, ඔබට ශූන්‍ය දෛශිකයක් (zero vector) ගැනත් කතා කළ හැකියි. නමින්ම කියනා පරිදි එහි අගය 0යි. ඒ කියන්නේ කිසිදු දෛශිකයක් නැතැයි යන්නයි. කිසිදු දිශාවක් එනිසා ඊට කිව නොහැකියි. ඇත්තටම ශූන්‍ය දෛශිකය යනු කිසිවක් නොවේ; එනිසා දෛශිකයක්ද නොවේ යැයි කෙනෙකුට තර්ක කළ හැකියි. එනිසා දෛශිකයක් හා අදිශයක් සමාන වන එකම අවස්ථාව ශූන්‍ය දෛශිකයයි (හරියට 0 යන අගය තාත්වික සංඛ්‍යා හා අතාත්වික සංඛ්‍යා දෙකටම අයත් වන්නා සේ). ශූන්‍ය දෛශිකය තද අකුරින් 0 ලෙස හෝ 0 ලෙස හෝ නිරූපණය කළ හැකියි.

යම් දෛශිකයක සලකුණ (ධන හෝ ඍන) වෙනස් කළ විට, එම දෛශිකයේ විශාලත්වය වෙනස් නොවී දිශාව ප්‍රතිවිරුද්ධ වේ.

 

දෛශික ගුණාකාරය

සමහරුන් මෙය “දෛශිකයක් අදිශයකින් ගුණ කිරීම” ලෙස හැඳින්වුවත් ඊට සුදුසුතම වචනය දෛශිය ගුණාකාරය (multiplication by scalar) බව මා යෝජනා කරනවා.

ඇත්තටම යම් දෛශිකයක් යම් අදිශයකින් ගුණ කරනවා යනුවෙන් සිතනවාට වඩා එය යම් දෛශිකයක විශාලත්වය ලොකු කුඩා කරනවා (scaling) යනුවෙන් සිතීම වඩා සුදුසුය. උදාහරණයක් ලෙස, යම් දිශාවක් ඔස්සේ බලය (එය දෛශිකයකි) නිව්ටන් 20ක් නම්, එහි අගය 100 කිරීමට නම්, එම බලය 5 ගුණයකින් ගුණ කළ යුතුයිනෙ. එහෙමත් නැතිනම් එම බලය 10 කිරීමට, එම බලය 2 ගුණකයකින් බෙදිය (හෙවත් ½ න් ගුණ කළ) යුතුය. මෙලෙස දෛශිකයේ විශාලත්වය අඩු හෝ වැඩි කිරීම තමයි මෙම ගණිත කර්මයේ එකම අරමුණ.

ඉතිං එය බැලූ බැල්මට පෙනෙන්නේ යම් දෛශිකයක් අදිශයකින් ගුණ කරනවා වගේය. නිකංම අගයන් දෙක ගුණ කරන්න පමණයි තිබෙන්නේ. ලැබෙන පිළිතුර හැමවිටම දෛශිකයකි.

5 x 20 N = 100 N

½ x 20 N = 10 N

අගයන් දෙක ගුණාකාරය තුල තිබෙන පිලිවෙල වැදගත් නැත. මෙම ගතිගුණයට න්‍යාදේශ්‍ය න්‍යාය (commutative law) යැයි කියනවා.

5 x 20 N = 20 N x 5

½ x 20 N = 20 N x ½

මෙම ගණිත කර්මය සංඝටන න්‍යාය (associative law) පිලිපදී. එනම්, යම් දෛශිකයක් ගුණාකාර (අදිශ) දෙකකින් ගුණ කරන විට, පහත ආකාරයේ රටාවට අනුගත වේ.

(4 x 5) x 20 N = 4 x (5 x 20 N)

තවද, මෙම ගණිත කර්මය විඝටන න්‍යාය (distributive law) පිලිපදී. එනම්, දෛශික පද දෙකක් එකම ගුණාකාරයකින් ගුණ වන විට හෝ දෛශික පදයක් ගුණාකාර පද දෙකක එකතුවකින් ගුණ වන විට, පහත රටාවලට එය අනුගත වේ.

4(20 N + 15 N) = 4x20 N + 4x15 N

(3 + 6)20 N = 3x20 N + 6x20 N

සටහන

ගණිතයේදී, පදයක් (term) යනු එකතු කිරීමකින් (+ ලකුණකින්) හෝ අඩු කිරීමකින් (- ලකුණකින්) වෙන්ව ඇති හෝ දෙපස කිසිදු ගණිත කර්මයක් නැති (තනියෙන්ම සිටින) රාශියකි.

10 + 19 (10 හා 19 යනු පද දෙකකි)

12² – 20 + x (12², 20, හා x යනු පද තුනකි)

2x20 + 30/3 + 12 (2x20, 30/3, හා 12 යනු පදක තුනකි)

t (t යනු පදයකි)

ඉහත සුලු කිරීම් සියල්ලෙහිම දෛශිකය කිසිදු ඛණ්ඩාංක පද්ධතියක් ඇසුරින් නෙමෙයි දක්වා තිබෙන්නේ. ඒ කියන්නේ කුමන ඛණ්ඩාංක පද්ධතියක් ඇසුරින් දෛශික නිරූපණය කළත් ඉහත කරුණු සියල්ල එලෙසම ගැලපේ. අප මෙතෙක් සලකා බැලුවේ කාටිසියානු පද්ධතිය පමණක් නිසා, ඒ ඇසුරින් උදාහරණ කිහිපයක් සලකා බලමු.

5 x (3i + 2j + 5k) = 15i + 10j + 25k (සාමාන්‍ය දෛශික ගුණාකාරය)

5 x (3i + 2j + 5k) = (3i + 2j + 5k) x 5 (න්‍යාදේශ්‍ය න්‍යාය)

(2 x 5) x (3i + 2j + 5k) = 2 x (5 x (3i + 2j + 5k)) (සංඝටන න්‍යාය)

4((3i + 2j + 5k) + (2i + 6j +2k)) = 4(3i + 2j + 5k) + 4(2i + 6j + 2k)

(5 + 2)(3i + 2j + 5k) = 5(3i + 2j + 5k) + 2(3i + 2j + 5k) (විඝටන න්‍යාය)

දෛශික ආකලනය

දෛශික දෙකක් එකට එකතු කිරීම දෛශික ආකලනයයි (vector addition). සාමාන්‍ය සංඛ්‍යා දෙකක් එකට එකතු කරන ආකාරයටම දෛශික දෙකක් එකතු කළ හැකියි එම දෛශික දෙකම එකම දිශාවට පිහිටියේ නම් පමණක්. තවද, දිශා දෙක එකිනෙකට ප්‍රතිවිරුද්ධ නම්, විශාල අගය තිබෙන දෛශිකයෙන් කුඩා අගය තිබෙන දෛශිකය අඩු කර, විශාල අගය තිබෙන දෛශිකයේ දිශාවට සුලු කර ලැබෙන අවසාන දෛශිකයේ දිශාව තැබිය යුතුය.

එහෙත් දෛශික දෙකෙහි දිශා ඉහත අවස්ථා දෙකට වඩා වෙනස් නම්, එවිට වෙනත් ආකාරයකින් එම එකතු කිරීම සිදු කළ යුතුය. පළමුව එය රූපමය ආකාරයෙන් බලමු. එක් දෛශිකයක් පළමුව කොලය මත අඳින්න. ඉන්පසු එම දෛශිකය කෙළවර වන තැන සිට දෙවැනි දෛශිකය එහි දිශාව ඔස්සේ අඳින්න. මෙවිට එම දෛශික දෙකෙහි එකතුව/ආකලනය වනුයේ පළමු දෛශිකය පටන් ගත් ස්ථානයේ සිට දෙවැනි දෛශිකය කෙලවර වන ස්ථානය දක්වා අඳින ඉරි කැබැල්ලෙන් නිරූපණය කෙරෙන දෛශිකයයි.

ඉහත රූපයම පහත ආකාරයටද ඇඳිය හැකිය. එය සමාන්තරාස්‍රයකි (parallelogram). සාමානතරාස්‍රයක් ආකාරයට (රූපමය වශයෙන්) දෛශික ආකලනය සිදු කිරීමේ එම ක්‍රමය සමාන්තරාස්‍ර නියමය (parallelogram law) ලෙස හැඳින්වේ.

රූපමය ආකාරය දෛශික ආකලනය තේරුම් ගැනීමට පහසු වුවත්, ඉක්මනින් හා නිවැරදිව සුලු කිරීමට එය උචිත නැත. තවද, ඉන් පිලිතුර ලෙස ලැබෙන දෛශිකයේ දිශාවද නිශ්චිතව දැනගත නොහැකිය. ඒ නිසා හරියටම විශාලත්වය හා දිශාව සොයා ගැනීමට සුත්‍රයක් යොදා ගත යුතුය. දෛශක ආකලනය සිදු කිරීමට කොස් සූත්‍රය (cosine formula හෙවත් law of cosines) යොදා ගත හැකිය. පහත දැක්වෙන්නේ ත්‍රිකෝණමිතියෙන් අපට ලැබෙන ඉතා වැදගත් කොස් සූත්‍රය වේ.

එකතු කළ යුතු දෛශික දෙක (b හා c යැයි සිතමු) හා ඒ අතර පවතින කෝණය (A) ඉහත සූත්‍රයට ආදේශ කළ විට ලැබෙන්නේ එම දෛශික දෙකෙහි ඓඛ්‍යය (a) වේ. තවද, එම නව දෛශිකයේ දිශාවද අපට සෙවිය හැකියි නැවත කොස් සූත්‍රය යෙදීමෙන්.

සටහන
ත්‍රිකෝණයක පාද හා ශීර්ෂ නම් කරන සම්මත ක්‍රමයක් ඇත. එනම්, ත්‍රිකෝණයක ශීර්ෂ ඉංග්‍රිසි කැපිටල් අකුරුවලින් පිලිවෙලින් වටේට ලකුණු කෙරේ. එවිට එම ශීර්ෂයට අනුබද්ධව පවතින අභ්‍යන්තර කෝණයද එම කැපිටල් අකුරෙන්ම සංඛේතවත් කෙරේ. තවද, ත්‍රිකෝණයේ පාද ලකුණු කරන්නේ ඉංග්‍රිසි සිම්පල් අකුරුවලිනි. එහිදී, යම් ශීර්ෂයකට විරුද්ධ පැත්තේ ඇති පාදය එම ශීර්ෂය ලකුණු කළ අකුරේම සිම්පල් අකුරින් ලිවිය යුතුය. ඉහත ත්‍රිකෝණය මෙලෙස ලකුණු කර ඇති සම්මත ත්‍රිකෝණයකි. මෙලෙස ත්‍රිකෝණයක කොටස් ලකුණු කිරීමෙන් පහසුවෙන් තනි අකුරකින් පාද හා කෝණ සටහන් කළ හැකිය. නැතහොත් පාද නම් කරන විට, AB, BC ආදි ලෙස අක්ෂර දෙකකින්ද, කෝණ නම් කරන විට, ABC, BCA ආදි ලෙස අක්ෂර 3කින්ද ලකුණු කිරීමට සිදු වෙනවානෙ.

පහත දැක්වෙන a (එහි අගය 10 ලෙස ගමු), b (අගය 20 ලෙස ගමු) දෛශික දෙක එකතු කරන හැටි බලමු. එම දෛශික දෙක අතර කෝණය අංශක 120කි. දැන් මීට කොස් සූත්‍රය යෙදූ විට පහත ආකාරයට සුලු වේවි.

(a + b)² = a² + b² - 2abcosA

(a + b)² = 10² + 20² - 2x10x20xcos(120) = 700

(a + b) = √700 = 26.5

ඉහත 26.5 අගය ලැබුණු දෛශිකයේ දිශාව කුමක්ද? එය අනෙක් දෛශික දෙකෙන් එකක දිශාව ආශ්‍රයෙන් ප්‍රකාශ කළ හැකිය (එම දෛශික දෙක අප දන්නවානෙ; දෛශිකයක් දන්නවා යනු එහි විශාලත්වය හා දිශාව දන්නවා කියන එකයි). උදාහරණයක් ලෙස a නම් දෛශිකය සිරස් අතට ඇඳි රේඛාවකට (සිරසට සාපේක්ෂව) ඇති කරන කෝණය Ω නම්, a+b නම් දෛශිකයේ දිශාව වන්නේ (Ω + θ) වේ (සිරසට සාපේක්ෂව). θ කෝණය අපට සෙවිය හැකියි නැවතත් කොස් සූත්‍රය යෙදීමෙන්. ඉහත උදාහරණයම ගතහොත්, x = 10, y = 26.5, (x+y) = 20 බව පෙනේ.

(x + y)² = x² + y² - 2xycosθ

cosθ = {x² + y² - (x + y)²}/2xy

θ = cos ^-1[{x² + y² - (x + y)²}/2xy]

θ = cos^-1[{10² + 26.5² - (20)²}/(2x10x26.5)] = 40.7^o

දෛශික දෙක අතර කෝණය හරියටම අංශක 90ක් වන විට, කොස් සූත්‍රය පයිතගරස් ප්‍රමේයය/සූත්‍රය බවට සරල වේ. එවිට නව දෛශිකයේ විශාලත්වය හා දිශාව යන දෙකම සුලු කිරීම තවත් පහසු වේ.

 

දෛශික ආකලනය න්‍යාදේශ්‍ය න්‍යාය පිළිපදී.

a + b = b + a

 

එය සංඝටන න්‍යායත් පිළිපදී.

(a + b) + c = a + (b + c)

මෙහිදී විඝටන න්‍යායක් ගැන සාමාන්‍යයෙන් කතා කරන්නේ නැත. ඉහත කරුණු සියල්ලම ඛණ්ඩාංක පද්ධතියක් ඇසුරින් නිරූපණය කරන දෛශික සඳහාද වලංගු විය යුතුයිනෙ. ඒ ගැන දැන් සොයා බලමු. ඇත්තටම මෙහිදී තත්වය තවත් පහසු වේ. කරන්නට තිබෙන්නේ දෙන ලද දෛශික දෙකෙහි අනුරූප සංරචක කොටස් එකිනෙකට එකතු කිරීම පමණි.

(3i + j - 5k) + (2i + 11j + 3k) = (3 + 2)i + (1 + 11)j + (-5 + 3)k = 5i + 12j - 2k (සාමාන්‍ය ආකලනය)

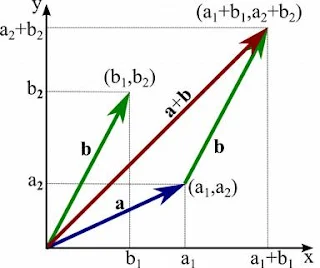
ඉහත රූපයේ වෙන වෙනම අනුරූප සංරචක එකතු කරන හැටි පැහැදිලිව දැක්වේ (ද්විමාන අවකාශයකි මෙහිදී සලකා තිබෙන්නේ). රූපය අනුව, (a + b) = (a₁i + a₂ j) + (b₁i + b₂i) = (a₁+b₁)i + (a₂+b₂)j වේ.

(3i + j - 5k) + (2i + 11j + 3k) = (2i + 11j + 3k) + (3i + j - 5k) (න්‍යාදේශ්‍ය)

((3i + j - 5k) + (2i + 11j + 3k)) + (i + j + k) = (3i + j - 5k) + ((2i + 11j + 3k) + (i + j + k)) (සංඝටන)

දෛශික ව්‍යාකලනය

එක් දෛශිකයක් තවත් දෛශිකයකින් අඩු කිරීම දෛශික ව්‍යාකලනයයි (vector subtraction). ඇත්තටම මෙයත් ඉහත පෙන්වාදුන් දෛශික ආකලනයේම විශේෂ අවස්ථාවක් ලෙස සැලකිය හැකියි. දෛශිකවල පමණක් නොව, සාමාන්‍ය සුලු කිරීම්වලදී පවා අඩු කිරීම යනු එකතු කිරීමෙහිම විශේෂ අවස්ථාවක් ලෙස සැලකිය හැකිය. එහිදී, අඩු කළ යුතු දෛශිකය දැනට පවතින සලකුණ (ධන හෝ ඍන) මාරු කර, එකතු කිරීමක් ලෙස ලිවිය හැකිය. ඔබ මොහොතකට පෙර දැන ගත්තා යම් දෛශිකයක සලකුණ මාරු වෙනවා යනු එහි විශාලත්වය වෙනස් නොවී දිශාව ප්‍රතිවිරුද්ධ වීමයි.

a - b = a + (-b)

එනිසා දෛශික ව්‍යාකලනය සලකුන මාරු කර දෛශික ආකලනයක් බවට පත් කර ගෙන කොස් සූත්‍රය (හෝ කෝණ අගය අංශක 90 නම් පයිතගරස් ප්‍රමේයය) භාවිතා කරමින් පුරුදු ලෙසම සුලු කළ හැකිය. තවද, දෛශික ආකලනයේදී හමු වූ න්‍යාදේශ්‍ය, සංඝටන, හා විඝටන න්‍යායවල් සියල්ල මෙහිදිත් වලංගු වේ.