දෛශික අවකලනය
දෛශික රාශි
මත අවකලනය (differentiation)
සිදු කළ
හැකියි.
ඇත්තටම
අවකලනය (හෝ
අනුකලනය)
සිදු
කරන්නේ නිකංම රාශියක් (දෛශික
හෝ අදිශ)
මත නොව,
එම රාශිය
ඇතුලත් ශ්රිතයක් (function)
මතයි.
එනිසා
දෛශික ඇතුලත් ශ්රිත ගැන
මුලින්ම දත යුතුය.
ඔබ දන්නවා
ශ්රිතයක් කියන්නේ ස්වායත්ත
විචල්ය එකක් හෝ කිහිපයක්
ඇතුලත් පහත ආකාරයේ ගණිතමය
ප්රකාශවලටයි.
ශ්රිතය
නම් කරන්නේ y,
t, s වැනි
අකුරකින් හෝ f(x),
f(x,y), g(t) වැනි
නිරූපණ ක්රමයකිනි.
මෙම නමට
පරායත්ත විචල්ය (dependent
variable) කියා
කියනවා (=ට
දකුණු පස ඇති ප්රකාශය තනි
අගයක් බවට සුලු වී මෙම පරායත්ත
විචල්යයේ අගය බවට පත් වේ).
f(x) වැනි
නිරූපණ ක්රමය නිකංම ඉංග්රිසි
අකුරකින් නම් කරනවාට වඩා
යෝග්ය වේ මොකද එහි වරහන් තුල
ශ්රිතයේ තිබෙන ස්වායත්ත
විචල්ය (independent
variable) සියල්ල
නම් කරනවා.
f(x) = x2
+ 3x - 2
y = 2x4
- x + 54
f(x,y) = x2
- 3xy + y3
අප දෛශික
ශ්රිතයක් (vector
function හෝ
vector-valued
function) යනුවෙන්
සාමාන්යයෙන් හඳුන්වන්නේ
පරායත්ත විචල්යය දෛශික
රාශියක් වන අවස්ථාවයි (එම
ශ්රිතයේ ස්වායත්ත විචල්යයන්
අදිශ හෝ දෛශික විය හැකිය).
පහත ආකාරයට
එවැනි ශ්රිතයක් නිරූපණය
කෙරේ.
දෛශික
බව හැඟවීමට සුපුරුදු උපක්රමයක්
ශ්රිතය හඟවන අක්ෂරය මත යොදන්න.
පළමු
පේලියේ තිබෙන්නේ අදිශ ස්වායත්ත
විචල්ය වන අවස්ථාවක් වන අතර,
දෙවැනි
පේලියේ තිබෙන්නේ දෛශික ස්වායත්ත
විචල්යයක් සහිත අවස්ථාවයි.
a
= F(x)
හෝ a
= F(x)
a
= F(R)
හෝ a
= F(R)
සාමාන්යයෙන්
ඔබ ශ්රිත ලෙස ඉගෙන ගෙන තිබෙන්නේ
ස්වායත්ත විචල්ය මෙන්ම
පරායත්ත විචල්යයද අදිශ වන
අවස්ථාය.
ඒවා අදිශ
ශ්රිත (scalar
function හෝ
scalar-valued
function) යටතට
වැටේ.
ඇත්තටම
අදිශ ශ්රිතයක ස්වායත්ත
විචල්යද අදිශ හෝ දෛශික විය
හැකිය.
එවැනි
ශ්රිත පහත ආකාරයට ලිවිය
හැකිය.
a
= F(x)
හෝ a
= F(x)
a
= F(R)
හෝ a
= F(R)
දෛශික ශ්රිත
අවකලනය කරන ආකාරය සාමාන්ය
(එනම්
අදිශ ශ්රිත අවකලනය කිරීම)
ආකාරයටම
සිදු වේ (පහත
දැක්වෙන ලෙසට).
බලන්න
අවකලන සූත්රයේ කිසිදු වෙනසක්
නැහැනෙ.
ඇත්තටම
අවකලනය සඳහා යොදා ගන්නා සෑම
නිරූපණය ක්රමයක්ම මෙහිදී
වලංගු වන අතර,
දෛශික
බව හැඟවීමට සුදුසු උපක්රමයක්
පමණයි අමුතුවෙන් යෙදීමට අවශ්ය
වන්නේ (අක්ෂරය
තද කිරීම හෝ ඊට උඩින් ඉරි
කැබැල්ලක් යෙදීම වැනි).
සටහන
කලනය
කලනය
(calculus)
ප්රධාන
කොටස් දෙකකි -
අවකලනය
හා අනුකලනය.
අවකලනය
හා අනුකලනය යනු එකතු කිරීම,
බෙදීම
වැනිම තවත් ගණිත කර්ම දෙකකි.
එකතු
කිරීමට අඩු කිරීම පවතින්නා
සේ,
ගුණ
කිරීමට බෙදීම පවතින්නා සේ,
අවකලනයට
අනුකලනය පවතී (එකිනෙකට
ප්රතිවිරුද්ධ ගණිත කර්ම
ගණිතයේ තිබෙනවානෙ).
එහෙත්
එකතු කිරීම,
ගුණ
කිරීම ආදි ගණිත කර්මවලට වඩා
කලන ගණිත කර්ම සංකීර්ණ හා
අපහසු වේ.
අවකලනයේදී
සිදු කරන්නේ දෙන ලද ශ්රිතයක්
එහි ඇති යම් ස්වායත්ත විචල්යයකට
සාපේක්ෂව විචලනය වන
සීඝ්රතාව(rate
of change)
ගණනය
කිරීමයි.
උදාහරණයක්
ලෙස,
කාලයට
සාපේක්ෂව යමක් ගමන් කරන දුර
වෙනස් වීමේ සීඝ්රතාව යනු
එහි වේගයයි (තත්පරයට
කොච්චර මීටර් ගණනක වේගයෙන්
යන්නේද කියන එක).
ඒ
කියන්නේ දුර යන (පරායත්ත)
විචල්යය,
කාලය
යන (ස්වායත්ත)
විචල්යයට
සාපේක්ෂව වෙනස් වීමේ සීඝ්රතාව
සෙවිය හැකියි අවකලනයෙන්.
අවකලන
ගණිත කර්මය පහත ස්වරූපයෙන්
ලියයි.
ඉහත
dF(t)/dt
යන
අවකලන නිරූපණය
ශබ්ද කරන්නේ "t
විෂයෙන්
F
ශ්රිතය
අවකලනය කිරීම"
යනුවෙනි
(Differentiation
of F
of t
with respect to t).
මෙහි
"අහවල්
විෂයෙන්"
යනු
"අහවල්
දේට සාපේක්ෂව"
කියන
එකම තමයි.
අවකලනය
යනු තනි ගණිත කර්මයක් වුවත්,
එය
සුලු කරන විධික්රම ගණනාවක්ම
තිබේ.
ඒවා
අවකලන සාම්යයන්
(differentiation
identities)
ලෙස
හැඳින් වේ.
සාම්යයක්
යනු යම් සුලු කිරීමක් කිරීමට
ඇති තවත් ක්රමයකි;
බොහෝවිට
මෙම අනෙක් ක්රමය වඩා පහසුය.
එකතු
කිරීම,
වැඩි
කිරීම වැනි ගණිත කර්ම සරල වැඩි
නිසා ඒ
සඳහා
සාම්යයන්වල අවශ්යතාවක්
නැත.
එම
සාම්යයන් කටපාඩම් කළ විට
ඉක්මනින් හා පහසුවෙන් අවකලනය
සිදු කළ හැකිය.
එම
සාම්යයන් අතර ඉතා වැදගත්
සාම්යයකි පහත දැක්වෙන දාම
රීතිය (chain
rule).
මෙම
ප්රකාශය ඔබට ඕනෑ තරම් දිගු
කරගෙන යා හැකියි එම රටාව අනුගමනය
කරමින් (රටාව
පැහැදිලි වීම පිනිස වර්ණ කර
ඇත).
වරක්
අවකලනය කළ පසු ලැබෙන පිලිතුරද
ශ්රිතයක් නම්,
නැවත
එය එම විෂයෙන්ම අවකලනය කළ
හැකියි.
එකම
විෂයෙන් දෙවැනි වරටත් අවකලනය
කිරීම d2F(t)/dt2
ලෙසද,
තෙවැනි
වරටත් අවකලනය කිරීම d3F(t)/dt3
ලෙසද
ආදි වශයෙන්
නිරූපණය කළ හැකිය.
යම්
ශ්රිතයක් අවකලනය කළ හැක්කේ
වරකට එක් විෂයකින් පමණි.
එනිසා,
යම්
ශ්රිතයක් තුල ස්වායත්ත
විචල්යයන් කිහිපයක් ඇති විට
මෙය විශේෂත්වයක් ඇති කරනවා.
එහිදී
ස්වායත්ත විචල්ය කිහිපයෙන්
තමන්ට අවශ්ය විචල්යයක්
විෂය කොට ගෙන අවකලනය සිදු
කරනවා.
මෙවිට
අවකලනය "පාර්ශ්වික
අවකලනය"
(partial differentiation)
ලෙස
හඳුන්වනවා.
එය
සංඛේතවත් කරන්නේ පහත ආකාරයටයි.
මෙහි
පළමු ප්රකාශයේදී පාර්ශ්වික
අවකලනය සිදු කරන්නේ x
විෂයෙන්
වන අතර,
දෙවැනි
ප්රකාශයේදී පාර්ශ්වික අවකලනය
සිදු කරන්නේ y
විෂයෙනි.
පාර්ශ්වික
අවකලනයක් සාමාන්ය (පූර්ණ)
අවකලනයක්
බවට පත් කළ හැකියි පහත සූත්රයෙන්.
මේ
සඳහා ශ්රිතයේ ඇති ස්වායත්ත
විචල්ය තවත් විචල්යයක ශ්රිත
ලෙස කටයුතු කළ යුතුය (පහත
ප්රකාශයේදී x,
y, z යන
u
ශ්රිතයේ
විචල්ය 3ම
නැවතත් t
විචල්යයේ
ශ්රිත වේ).
විචල්යක්
තුල විචල්යයක් ලෙස ක්රියා
කරන පදය පරාමිතිය (parameter)
ලෙස
හඳුන්වමු (ඒ
අනුව t
යනු
පරාමිතියයි).
දාම
රීතිය මෙහි යොදා ගෙන තිබේ.
මෙහි
u
යනු
විචල්ය කිහිපයක ශ්රිතයකි;
විචල්ය
ගණන ඕනෑම ගණනක් විය හැකියි
(පහත
ප්රකාශයේදී විචල්ය 3ක්
ඇත).
එවිට
එම ශ්රිතය පළමුව එක් විචල්යයකින්
පාර්ශ්වික අවකලනය කරයි
(∂u/∂x).
ඉන්පසු,
එම
ස්වායත්ත
විචල්ය
පරාමිතියෙන් අවකලනය කර
(dx/dt),
මීට
පෙර ලැබුණු අගය සමඟ ගුණ කළ
යුතුය
((∂u/∂x).(dx/dt)).
මෙලෙසම
අනෙක් විචල්යවලටත් සිදු කර,
ඒවා
සියල්ල එකතු කළ විට ලැබෙන අගය
මුල්ම ශ්රිතය කෙලින්ම
පරාමිතියෙන් අවකලනය කර ලැබෙන
අගයට සමාන වන බවයි මෙම සූත්රයෙන්
කියන්නේ.
විචල්ය
ගණනට සමාන
(∂u/∂x).(dx/dt)
වැනි
කොටස් ගණනක් පවතීවි.
යම්
කිසි නියත පදයක් ඕනෑම විෂයකින්
අවකලනය කළ විට පිලිතුර ශූන්ය
වේ.
එලෙසම,
ස්වායත්ත
විචල්ය එකක් හෝ කිහිපයක්
සහිත යම් ශ්රිතයක් එම ශ්රිතයේ
නැති විචල්යයකින් අවකලනය
කළොත්,
එවිටද
ශ්රිතය එම විෂය/විචල්යය
මත රඳා නොපවතින නිසා,
නියත
පදයක් අවකලනය කරන විට මෙන්ම
ශූන්ය වේ.
අනුකලනය
යනු අවකලනයේ විරුද්ධ ක්රියාවයි.
එනම්
යම් ශ්රිතයක් අවකලනය කිරීමෙන්
පසු ලැබෙන පිලිතුර අනුකලනය
කළ විට නැවත ලැබෙන්නේ මුල්
ශ්රිතයයි.
අනුකලනයද
තනි ගණිත කර්මයක් වුවත් විවිධ
ස්වරූපයේ ශ්රිතවලට එය සිදු
කරන විට පහසුවෙන් සුලු කිරීම
පිනිස අනුකලන සාම්යයන්
සාදා ගෙන තිබේ.
පහත
දැක්වෙන්නේ අනුකලනය ලියන
ස්වරූපයයි.
එය
ශබ්ද කරන්නේ "t
විෂයෙන්
F
ශ්රිතය
අනුකලනය කරනවා"
කියාය.
dt ආදි
ලෙස දක්වන්නේ විෂය පදයයි (t).
අනුකලනය
කළ පසු ලැබෙන්නේ ශ්රිතයකි.
එම
ශ්රිතය නැවත එම විෂයෙන්ම හෝ
වෙනත් විෂයකින් අනුකලනය කළ
හැකියි.
එලෙස
නැවත නැවත අනුකලනය කළ හැකියි.
අනුකලනය
කරන වාර ගණනට සමාන ගණනක් අනුකල
සංඛේතයද විෂය පදද තිබිය යුතුය.
පහත
නිරූපණ බලන්න.
පාර්ශ්වික
අවකලනයට අනුරූපව පාර්ශ්වික
අනුකලනය කියා දෙයක් අමුතුවෙන්
අවශ්ය නැති බව පේනවා නේද?
අනුකලනයේ
විශේෂිත ස්වරූපයක් තිබෙනවා
නිශ්චිත අනුකලනය (definite
integration)
නමින්.
එහිදී
සාමාන්ය පරිදි අනුකලනය
ශ්රිතය (එය
F(t)
යැයි
සිතමු)
මත
සිදු කර,
ඉන්පසු
පිලිතුර ලෙස ලැබෙන ශ්රිතයේ
(f(t)
යැයි
කියමු)
ස්වායත්ත
විචල්යයට
(t
යැයි
සිතමු)
දෙන
ලද යම් අගයක් (b
යැයි
එම අගය නම් කරමු)
ආදේශ
කර එම ශ්රිතය නිශ්චිත අගයක්
(f(b))
බවට
පත් කර ගනී.
නැවතත්
එම පිලිතුරු ශ්රිතයට දෙන ලද
තවත් අගයක් (a
ලෙස
එය නම් කරමු)
ආදේශ
කර ශ්රිතය නැවතත් තවත්
අගයක්
(f(a))
බවට
පත් කර ගනී.
දැන්
මෙම දෙවැනියට ලැබුණු අගය
පළමුවෙන් ලැබුණු අගයෙන් අඩු
කරන්න.
එච්චරයි.
මෙම
ක්රියා දාමය සම්මත ආකාරයෙන්
සංක්ෂිප්තව ඉදිරිපත් කරන්නේ
පහත ආකාරයටයි (ඒ
කියන්නේ පහත දැක්වෙන්නේ
නිශ්චිත අනුකලනයේ නිර්වචනයයි).
අවකලනය
හා අනුකලනය ගැන හොඳ දැනුමක්
තිබිය යුතුයි දෛශික කලනය
(vector
calculus)
ගැන
ඉගෙන ගන්නට නම්.
ඉහත
සිදු කළේ සුලු මතක් කිරීමක්
පමණි.
දෛශික
අවකලනයකට උදාහරණයක් බලමු.
යම්
අංශුවක් R
නම්
පථයක් ඔස්සේ ගමන් කරනවා යැයි
සිතමු.
එම
පථය නිශ්චිතව R
= (t2
+ 3t)i + (t-5)j + t3k
ලෙස
දී ඇතැයි සිතන්න.
මෙහි
t
යන
ස්වායත්ත විචල්යය කාලය
නියෝජනය කරනවා නම්,
එම
t
(කාලය)
විෂයෙන්
එම පථය අවකලනය කරන්න.
පථයක්
යනු දුරකි/විස්ථාපනයකි.
යම්
විස්ථාපනයක් කාලය විෂයෙන්
අවකලනය කරන විට (එනම්
විස්ථාපනය කාලයෙන් බෙදන විට),
අපට
ලැබෙන්නේ ප්රවේගයකි.
සාමාන්යයෙන්
භාවිතා කරන අවකලන සාම්යයන්
ගණනාවක්ම
දෛශික අවකලනයේදිත් භාවිතා
කළ හැකිය.
මා
ඒවා පහත දක්වා තිබෙනවා.
මෙම
සාම්යයන් තුල F,
G,
H
යනු
දෛශික ශ්රිතද,
θ යනු
සාමාන්ය/අදිශ
ශ්රිතයක්ද වේ.
c
හා
t
යනු
අදිශ රාශි
වේ.
දෛශික
ගුණාකාරය (3),
අදිශ
ගුණිතය (4),
දෛශික
ගුණිතය (5)
යන
අවස්ථා 3
සඳහාම
සාම්යයන් ඇති අතර එහි එකම
පොදු රටාව ඇත.
දෛශිකයක්
තවත් දෛශිකයකින් බෙදිය නොහැකි
නිසා දෛශික අනුපාතයක් (හෙවත්
බෙදීමක්)
සඳහා
සාම්යයක් ලිවිය නොහැකිය.
එහෙත්
දෛශිකයක් අදිශයකින් බෙදිය
හැකි නිසා ඊට සාම්යයක් ඇත
(6).
අවකලනයේදී
විෂය (හරය
ලෙස පවතින කොටස)
දෛශික
විය නොහැකිය මොකද මොනම
ක්රමයකින්වත් දෛශිකයක් හරය
ලෙස පැවතිය නොහැකි නිසා.
ඉහත
සාම්යයන් යොදා ගෙන අපි
උදාහරණයක්
බලමු.
a
= 2p i + 4p j - p2
k, හා
b
= sin(p) i + cos(p) යන
දෛශික දෙකෙහි තිත් ගුණිතය p
විෂයෙන්
අවකලනය කරන්න.
අවශ්ය
නම්,
පළමුව
දෛශික දෙක තිත් ගුණිතය සිදු
කර,
එය
අවකලනය කළ හැකියි.
මෙවිට
අවකලන සාම්යයක් යොදා ගැනීමට
අවශ්ය නැත.
නැතහොත්
පහත සුලු කිරීමේදී කර ඇති ලෙස
සාම්යයක් යොදා ගත හැකියි.
බලන්න
සාම්යය උපයෝගි කරගෙන සිදු
කර ලබා ගත් පහත අවසාන පිලිතුර
අදිශයකි.
තිත්
ගුණිතය අදිශියක් නිසා,
එය
අවකලනය කළ පසුත් ලැබිය යුත්තේ
අදිශයක්ම නේද?
ඉහත
දෛශික දෙකෙහි කතිර ගුනිතයද
p
විෂයෙන්
අවකලනය කරන්න.
මෙයද
පළමුව කතිර ගුණිතය සිදු කර,
ඒ
ලැබෙන පිලිතුර අවකලනය කළ
හැකියි.
කොහි
විදියට අවකලනය සිදු කළත් ලැබෙන
අවසාන පිලිතුර එකම විය යුතුය.
එය
දෛශිකයක් විය යුතුය.
ඩෙල් කාරකය
දෛශික
අවකලනයේදී හමුවන රසවත් සුලු
කිරීම් කිහිපයක්ම සිදු කරන්නකි
මෙම ඩෙල් කාරකය (del
operator).
එහි
සම්මත නිර්වචනය පහත ආකාරයෙනුයි
ඉදිරිපත් කරන්නේ.
හොඳින්
මෙම නිර්වචනය බලා එහි රටාව
පලමුව මතක තබා ගන්න.
ත්රිකෝණය
හැඩයෙන් සංඛේතවත් කරන්නේ
ඩෙල් කාරකයයි
(එය
"ඩෙල්"
කියා
ශබ්ද කෙරේ).
හැමවිටම
අදිශ හෝ දෛශික ශ්රිතයකට මෙය
යෙදිය යුතුය.
ඩෙල්
කාරකයෙන් කියන්නේ කුමක්ද?
නිර්වචනයේ
දැක්වෙන රටාව තේරුම් ගතහොත්
එය අවකාශීය මාන 3කට
දක්වා ඇති බව පෙනේ.
ඇත්තෙන්ම
එය මාන ඕනම ගණනකට සකස් කර ගත
හැකිය.
උදාහරණයක්
ලෙස,
පහත
දැක්වෙන්නේ මාන 5කට
එය සකස් කළේ නම්,
එය
දැක්විය හැකි ආකාරයයි.
මාන
දෙකකට හා එකකට එය අර්ථ දක්වන්නේ
නම් පිලිවෙලින් පහත ආකාරවලටද
ලිවිය හැකි බව පෙනේ.
කෙසේ
වෙතත්,
මාන
3ක්
සහිතවයි මෙම කාරකය ජනප්රියව
තිබෙන්නේ.
තවද,
මාන
ගණනට (ඒකක
දෛශික ගණනට)
සමාන
ස්වායත්ත විචල්ය ගණනක්
ශ්රිතය තුල ඇතැයි උපකල්පනය
කෙරෙන බවද පෙනේ මොකද එක් එක්
ඒකක දෛශිකයට වෙන් වූ විචල්ය
ඇත.
සමහරවිට
ශ්රිතය තුල මාන ගණනට වඩා අඩු
විචල්ය ගණනක් වුවද තිබිය
හැකි අතර,
එවිට
සුලු කිරීමේදී වැඩිපුර මාන
කොටස් ශූන්ය වී යයි මොකද
ශ්රිතය තුල නැති විචල්යයකින්
අවකලනය කරන විට නියත පදයක්
අවකලනය කරන විට ඇති වන තත්වය
මතු වේ (එවිට
පිලිතුර ශූන්ය වේ).
ඒ
කියන්නේ ඒකක දෛශික ගණන හා
විචල්ය ගණන ඉබේම සමාන වේ සුලු
කිරීමේදි.
තවද,
ඒකක
දෛශික ගණනට වඩා විචල්ය ගණන
වැඩි විය නොහැකිය.
ඉහත
පෙන්වා දුන්නේ ඩෙල් කාරකයේ
ව්යුහාත්මක
(ස්වරූපය
පිළිබඳ)
පැත්තයි.
එහි
කාර්යමය (මොනාද
කරන්නේ යන්න පිළිබඳ)
පැතිකඩ
කුමක්දැයි එකවරම කිව නොහැකිය.
ඊට
හේතුව එය කාර්යන්
3ක්
(ග්රැඩ්,
ඩිව්,
කර්ල්)
ඉටු
කරන නිසාය.
මේ
3ම
අවකලනය පාදක කර ගත් එකිනෙකට
වෙනස් ගණිත
කර්ම වේ.
ඒ
කියන්නේ ඩෙල් කාරකය යනු එක්තරා
විදියක අතරමැදි පහසුකම්
සපයන්නෙක් පමණි.
මෙම
අවස්ථා/කාර්යන්
3
වෙන
වෙනම දැනගත යුතුය.
මෙය
"කාරකය"
යන
වචනයෙන් හඳුන්වන්නට හේතුවක්
ඇත.
එනම්,
ඩෙල්
යනු ක්රියාවලියකට කියන නමක්
මිස යම් කිසි "දෙයක්"
නොවේ.
අදිශයක්
හෝ දෛශික යනු යම් යම් දේවල්
හෙවත් ගණිතමය වස්තුන්ය
(mathematical
objects). එහෙත්
"එකතු
කරන්න",
"අඩු
කරන්න"
ආදිය
යම් යම් ක්රියාවලි (කර්ම)
වේ.
ඩෙල්
කාරකයද එවැන්නකි.
එහෙත්
මොහොතකට පෙරත් සඳහන් කළ පරිදි
එය ඍජුවම ගණිත කර්මයක් නොවේ
එකතු කිරීම,
ගුණ
කිරීම,
අවකලනය
ආදිය මෙන්;
ග්රැඩ්,
ඩිව්,
කර්ල්
ආදි ගණිත කර්ම පහසුවෙන් හා
කෙටියෙන් නිරූපණය කිරීමට
ගන්නා අතරමැදි උපකාරකයක්
පමණි.
එය
ගණිතමය වස්තුවක් නොවන නිසාම
කාරකය යන නමින් හඳුන්වා දී
ඇත.


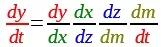







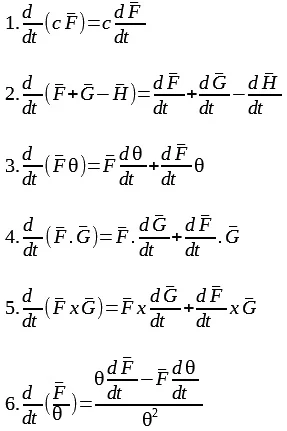
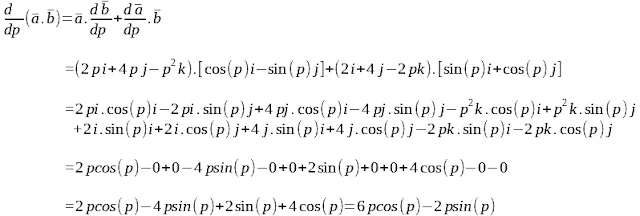




Comments
Post a Comment
Thanks for the comment made on blog.tekcroach.top