Antenna Efficiency
Radiation
Efficiency ලෙසද
හැඳින්වෙන ඇන්ටනා කාර්යක්ෂමතාව
හෙවත් ඇන්ටනා එෆිෂන්සි යනු
ඇන්ටනාවට (ට්රාන්ස්මීටරයෙන්)
සපයන විදුලි
ජවයට සාපේක්ෂව කොතරම් ජව
ප්රමාණයක් රේඩියෝ තරංග/විකිරණ
ලෙස පිට කරනවාද යන අනුපාතයයි.
මෙම අර්ථ
දැක්වීම ට්රාන්ස්මිටිං
ඇන්ටනාවක් ආශ්රයෙන් සිදු
කිරීම පහසුය. එහෙත්
රිසීවිං ඇන්ටනා හා ට්රාන්ස්මිටිං
ඇන්ටනා හැම අතින්ම සමාන නිසා,
ට්රාන්ස්මිටිං
ඇන්ටනාවක් සේ සලකා සොයා ගන්නා
ඇන්ටනා කාර්යක්ෂමතා අගය එලෙසම
රිසීවිං ඇන්ටනාවටත් අදාල වේ.
antenna efficiency = (radiated power) / (input electrical power)
මේ
අනුව හැමවිටම ඇන්ටනා කාර්යක්ෂමතා
අගය 0ත්
1ත්
අතර අගයකි. මෙම
අගය 1 නම්
ඒ කියන්නේ ඇන්ටනාවට සපයන
සියලුම විදුලි ජවය රේඩියෝ
තරංග බවට පත් වේ. එය
කිසිදා ප්රායෝගිකව සිදු
නොවන අතර, හැකි
තරම් කාර්යක්ෂමතාව 1ට
ළං කිරීමට උත්සහ කළ යුතුය.
අනුපාත
අගය දශම අගයක් ලෙස දැක්විය
හැකි වුවත්, බොහෝවිට
එය ප්රතිශතයක් හෝ ඩෙසිබල්
අගයක් ලෙස දක්වනවා.
ප්රතිශතයක්
බවට පත් කිරීමට නිකංම එම අනුපාත
දශම අගය 100න්
වැඩි කර % සලකුන
සමඟ යෙදීමයි කරන්නට තිබෙන්නේ.
උදාහරණයක්
ලෙස, කාර්යක්ෂමතාව
0.75 නම්,
ප්රතිශතයක්
ලෙස 75% වේ.
සුපුරුදු
ලෙසම ලඝු භාවිතා කරමින් ඩෙසිබල්
කළ හැකිය. උදාහරණයක්
ලෙස කාර්යක්ෂමතාව 0.5
හෙවත් 50%
නම්,
එය ඩෙසිබෙල්වලින්
-3dB වේ
(1ට වඩා
අඩු සෑම ඩෙසිබෙල් අගයක්ම ඍණ
සලකුණ සහිතව ලිවිය යුතුයිනෙ).
100%ක් කාර්යක්ෂම
නම්, ඩෙසිබෙල්
අගය 0dB වේවි.
ඇන්ටනාවක්
100% කාර්යක්ෂම
නොවීමට හේතු මොනවාද?
ඇන්ටනා
බට/සන්නායක
යනුද යම් ප්රතිරෝධයක් තිබෙන
සන්නායක වන නිසා, ඒවා
තුලින් ධාරාව ගලා යන විට තාපයක්
උත්සර්ජනය වේ. මෙය
conduction loss ලෙස
හැඳින්වේ. මෙම
තාප උත්සර්ජනය නිසා අපතේ යන්නේ
රේඩියෝ තරංග බවට පත් වීමට තිබූ
ජවයෙන් කොටසකි (ඒ
කියන්නේ සපයන ජවයට වඩා විකිරණය
වන ජවය අඩු වේ; කාර්යක්ෂමතාව
අඩු වේ). තවද,
සංඛ්යාතය
ඉහල වන විට චර්මීය ආචරණයේ
බලපෑම නිසා ඇන්ටනා බටවල/වයර්වල
ප්රතිරෝධය තවත් ඉහල යයි.
ඉන් තාප
උත්සර්ජනය තවත් වැඩි වී ඇන්ටනා
කාර්යක්ෂමතාව තවත් අඩු වේ.
ඇන්ටනාවට
ජවය සපයන්නේ ෆීඩ්ලයින් වයරයෙනි.
එම වයරයේ
සම්භාදකය/ප්රතිරෝධය
හා ඇන්ටනාවේ සම්භාදකය සමාන
නොවන විට, වයරය
දිගේ එන සම්පූර්ණ ජවය ඇන්ටනාවට
නොලැබේ (මේ
ගැන වැඩි විස්තර මොහොතකින්
සිදු කෙරේ). එවිට,
ඇන්ටනාවට
සපයපු ජවයෙන් කොටසක් භාවිතා
නොකර (එනම්
රේඩියෝ විකිරණ බවට පත් නොවී)
ආපසු
ට්රාන්ස්මීටරය වෙත යැවෙන
අතර එය තාපය ලෙස නාස්ති වේ
(impedance mismatch loss ලෙස
එය හැඳින්වේ); එමඟින්
ට්රාන්ස්මීටරය පිච්චීමට
පවා හැකියි. ට්රාන්ස්මීටරය
පිච්චුනත් නැතත්, මෙහි
ප්රතිපලයක් ලෙස විදුලි ජවයෙන්
කොටසක් විකිරණ ජවයක් බව පත්
නොවේ. එය
කාර්යක්ෂමතාව අඩු වීමකි.
ඇන්ටනාවක
ලෝහමය ඩයිපෝල් කූරු හැරුණහම
ප්ලාස්ටික්, ලී/දැව,
ෆයිබර්ග්ලාස්
ආදී පරිවාරක ද්රව්යද තිබෙනවානෙ
(ඇන්ටනා
කූරු සවි කරන පරිවාරක තැටිය
ආදිය). ඇත්තටම
මේවා නිසාද ඇන්ටනාව අවට ඇති
කම්පනය වන විද්යුත් හා චුම්භක
ක්ෂේත්රවල ජවයෙන් ඉතා සුලු
ප්රමාණයක් තාපය ලෙස උත්සර්ජනය
විය හැකියි (සාමාන්ය
විදුලි ට්රාන්ස්ෆෝමර්වලද
ශක්තිය මෙලෙස හානි වේ).
මෙම ජව
හානිය dielectric loss ලෙස
හඳුන්වමු.
මීටත්
අමතරව, ඇන්ටනාව
අවට ළඟම ඇති නියර් ෆීල්ඩ් හි
යම් යම් ලෝහමය හෝ අලෝහමය
ද්රව්ය/වස්තු
තිබුණොත්, විශාල
ලෙස ඇන්ටනාවෙන් නිකුත් වන
ශක්තිය ඒවා විසින් උරා ගැනේ.
එනිසා
ෆාර්ෆීල්ඩ් හි රේඩියෝ තරංග
සෑදීමට තිබූ ශක්තියයි එලෙස
අඩු වන්නේ. එයද
ඇන්ටනාවේ කාර්යක්ෂමතාව අඩු
වීමට හේතුවකි.
ඉහත
සඳහන් කළ ඇන්ටනාවක් අකාර්යක්ෂම
වීමට හේතු අතරින් ඉම්පීඩන්ස්
මිස්මැච් ලොස් එක තමයි අනෙක්
දෙකටම වඩා කැපී පෙනෙන ලෙස
පවතින්නේ. ඒ
සියලුම ආකාරයේ ජව හානි අවම
කළ හැකියි නිසි පියවර අනුගමනය
කිරීමෙන්. යකඩ
හෝ ඇලුමිනියම් ලෝහය වෙනුවට
තඹ ලෝහයෙන් ඩයිපෝල් බට සෑදිය
හැකියි කන්ඩක්ෂන් ලොස් අවම
කිරීමට. පසුව
පෙන්වා දෙන පරිදි චර්මීය
ආචරණයට හොඳින් මුහුන දෙන ලෙස
එම බට සෑදිය හැකියි. තවද,
ඇන්ටනාව හා
ෆීඩ්ලයින් යන දෙකෙහි සම්බාදක
අගයන් සමාන කළ හැකියි.
ඇන්ටනාව ළඟ
අවට ඇති අනවශ්ය දේ ඉවත්
කිරීමෙන් හා විදුලි ක්ෂේත්රයට
හා චුම්භක ක්ෂේත්රයට වැඩි
හායනයක් සිදු නොකරන පරිවාරක
ද්රව්ය යොදා ගත හැකියි.
ඇන්ටනාවක්
ඉබේම අකාර්යක්ෂම වනවා ඩයිපෝලය
අවශ්ය පමණට වඩා කෙටි වන විටත්.
සමහර ප්රායෝගික
හේතු නිසා ඇන්ටනාව ප්රශස්ථ
මට්ටමට වඩා කෙටි කිරීමට සිදු
වෙනවා (කුඩා
උපකරණයක් තුල ඇන්ටනාවක් සවි
කරන විට එහෙම). එවන්
ඇන්ටනා අකාර්යක්ෂම වේ.
මේ ගැන තවත්
විස්තර පසුවට ඇත.
Effective Aperture
දළ
වශෙයන් aperture යනු
ඇන්ටනාවේ සංඥා සම්ප්රේෂනය
කරන/ග්රහනය
කරන කොටසේ විශාලත්වයයි.
ඩයිපෝල්
ඇන්ටනාවක එය එහි දිග ලෙස ගත
හැකියි. ඩිෂ්
ඇන්ටනාවක ඩිෂ් එකේ ක්ෂේත්රපලය
ලෙස ගත හැකියි. ඇන්ටනා
සයිස් එක ලෙසද එය අවශ්ය නම්
හැඳින්විය හැකියි. ඇපචර්
එක වැඩි වන තරමට වැඩිපුර සංඥා
ග්රහණය කර ගැනීමට හැකියාව
ලැබේ (එනම්
සංඥා ප්රබලව ග්රහණය කර ගත
හැකියි).
එහෙත්
effective aperture හෙවත්
effective area යනු
නිකංම ඇන්ටනා සයිස් එකට එහා
ගිහිපු අදහසකි. මෙහිදී
ආදායක ඇන්ටනාවේ පොලරයිසේෂන්
එක හා ඉන් ග්රහනය කරන රේඩියෝ
සංඥාවල පොලරයිසේෂන් එක අතර
වෙනසක් නැතැයි උපකල්පනය කෙරේ
(එනම්
පොලරයිසේෂන් ලොස් ෆැක්ටර්
එක ශූන්ය වේ). තවද,
රිසීවිං
ඇන්ටනාවේ උපරිම ගේන් එක තිබෙන
දිශාව ඔස්සේ සංඥා ග්රහනය
කරන බවත් උපකල්පනය කෙරේ.
මෙම කොන්දේසි
යටතේ ඉෆෙක්ටිව් ඇපචර් (AER)
පහත සූත්රයේ
ආකාරයට සෙවිය හැකිය.
AER = PR/PD
මෙහි
PR යනු
රිසීවිං “ඇන්ටනාව විසින්
ග්රහනය කර ගත් සංඥා නිසා”
එම ඇන්ටනාවේ ප්රේරණය වූ මුලු
විදුලි ජවයයි. PD යනු
ඇන්ටනාවෙන් ග්රහනය කරනු ලබන
රේඩියෝ සංඥාවල සංඥා ජව ඝනත්වයයි
(රිසීවිං
ඇන්ටනාව තිබෙන ස්ථානයේ).
ජව ඝනත්වය
යනු වර්ගමීටරයකට තිබෙන වොට්
ගණනයි (Wm-2).
ඉහත
සමීකරණය හා විස්තරය අනුව,
ප්රායෝගිකව
ඇන්ටනාවේ ඇති විවිධාකාරයේ
සංඥා හායනයන් (losses) ඉබේම
සලකා බලා තිබේ (ආදායක
ඇන්ටනාවේ ප්රේරණය වන ජවය
යැයි පවසන විට එම සාධක ඇතුලත්
වී තිබේ).
ඕනෑම
ඇන්ටනා වර්ගයක් සඳහා පොදු/සාධාරණ
ඉෆෙක්ටිව් ඇපචර් අගය සොයන
සූත්රයක් පහත ආකාරයට දැක්විය
හැකිය. λ
යනු රේඩියෝ
තරංගයේ තරංග ආයාමය වන අතර,
GR
යනු ආදායක
ඇන්ටනාවේ ගේන් එක වේ.
සාමාන්ය
ඇන්ටනා සයිස් එක (aperture
හෙවත් physical
aperture) හා
ඉෆෙක්ටිව් ඇපචර් යන රාශි දෙකක්
දැන් අපට ඇත. මෙම
දෙකෙහි පහත ආකාරයට අනුපාත
අගය ගත් විට, ඊට
aperture efficiency යැයි
පවසනවා.
FSPL හා Friis Transmission Equation
Free Space Path
Loss (FSPL) යනු
රේඩියෝ තරංග අවකාශය (රික්තකයක්)
හරහා ගමන්
කිරීමේදී සම්ප්රේෂක ඇන්ටනාවේ
සිට ඈතට යන විට එම රේඩියෝ තරංගවල
ප්රබලතාවේ සිදුවන දුබලවීමයි.
මෙය ඇත්තටම
සංඥා හායනය වීමක් වගේ පෙනුනත්
සංඥා හායනයක් නොවේ. මෙහිදී
සිදුවන්නේ දුර වැඩි වන්නට
වන්නට රේඩියෝ තරංග ශක්තියට
වඩ වඩා විශාල ප්රදේශයක් ආවරණය
කිරීමට සිදු වීමයි (සංඥා
දියාරු වීමයි). උපමාවකින්
කියතොත්, සීනි
පිරුණු හැන්දක් කුඩා වතුර
වීදුරුවකට දැමූ විට එහි පැනි
රස වැඩි වුවත්, එම
සීනි හැන්දම විශාල වතුර භාජනයක
දිය කළොත් සීනි රස මතු නොවේ
(දියාරු
වේ).
පහත
සරල සූත්රයෙන් FSPL ගණනය
කළ හැකියි (මෙම
සූත්රය වලංගු වන්නේ ෆාර්ෆීල්ඩ්
එකේ පමණි). සම්ප්රේෂක
ඇන්ටනාව අයිසොට්රොපික් යැයි
උපකල්පනය කරමු. d යනු
සම්ප්රේෂක ඇන්ටනාවේ සිට
සලකා බලනු ලබන තැනට ඇති දුරයි.
λ
යනු
සම්ප්රේෂනය කරනු ලබන රේඩියෝ
තරංගයේ තරංග ආයාමය වන අතර,
f යනු එම
රේඩියෝ තරංගයේ සංඛ්යාතයයි.
c යනු
ආලෝකයේ වේගය වේ.
ඉහත
සූත්රය අනුව පෙනෙනවා මෙම
සංඥා දුබල වීම දුර වැඩි වන විට
ඉතා සීඝ්රයෙන් (වර්ග
පදයක් ලෙස) සිදු
වන බව. තවද,
සංඛ්යාතය
වැඩි වන විටත් එලෙසම සීඝ්රයෙන්
(වර්ග
පදයක් ලෙස) සංඥා
දුබල වේ. දුර
වැඩි වන විට සංඥාව දුබල වීම
ගැන මීට පෙරත් අප ඉගෙන තිබෙනවා
(ත්රිමාන
අවකාශයක පැතිරෙන ඕනෑම ක්ෂේත්රයකට
එය පොදුය). එහෙත්
සංඛ්යාතය වැඩි වන විට සංඥාව
දුබල වීම ගැන යමක් පැහැදිලි
කර ගත යුතු වේ.
ඇත්තටම
සංඛ්යාතය වැඩි වන විට සංඥා
ප්රබලතාව දුර්වල වන්නේ යම්
භෞතික න්යායක් නිසා නොවේ.
එය ප්රායෝගික
කරුණකින් සිදු වන්නක්.
සංඛ්යාතය
වැඩි වෙනවා යනු තරංග ආයාමය
අඩු වෙනවා යන්නනයි. එවිට
ඉබේම ඇන්ටනාවේ ඩයිපෝලයද කුඩා
වෙනවා. කුඩා
ඩයිපෝලයකට හසුවන්නේ සංඥා
කුඩා ප්රමාණයක් (ලොකු
බෑග් එකකට හුඟක් දා ගත හැකි
වුවද, කුඩා
බෑග් එකකට දා ගත හැක්කේ ටිකයිනෙ).
ඉතිං තරංග
ආයාමය කුඩා වීමෙන් එම සංඥා
ග්රහනය කරන ඇන්ටනාව කුඩා
වීම නිසා කුඩා සංඥා ප්රමාණයක්
පමණක් ග්රහණය වීම නිසා අවසානයේ
එය සංඥා ග්රහණය දුබල වීමක්
බවට පත් වෙනවා.
සමහර
අවස්ථාවල ඉහත සූත්රය ඩෙසිබෙල්
ආකාරයෙන්ද දක්වනවා. ඉහත
සූත්රය ඩෙසිබෙල්වලට හරවන
හැටි බලමු.
ඉහත
සූත්රය හා ඇන්ටනාව සම්බන්ද
තවත් පරාමිතින් කිහිපයක් එකට
ඇතුලත් කර සාදා ගත් තනි වැදගත්
සූත්රය තමයි ෆ්රිස්
ට්රාන්ස්මිෂන් සමීකරණය.
ෆ්රීස්
(Harold Friis) විසින්
මෙම සමීකරණය ව්යුත්පන්න කළ
බැවින් ඔහුගේ නමින් මෙම සූත්රය
නම් කර ඇත.
යම්
f සංඛ්යාතයක්
(λ
තරංග
ආයාමයක්)
සහිත
රේඩියෝ තරංගයක් G1
නම් ඇන්ටනා
ගේන් එකක් සහිත ලොස් නැති
පරිපූර්ණ සම්ප්රේෂක ඇන්ටනාවකින්
PT
ජවයකින්
විසුරවන විට,
ඊට R
දුරකින්
පිහිටි G2
නම් ගේන්
එකක් සහිත ලොස් නැති පරිපූර්ණ
ආදායක ඇන්ටනාවකින් එම සංඥා
ග්රහනය කරන විට,
ආදායක
ඇන්ටනාවට හසුවන ජවය (PR)
කොපමණදැයි
මෙම සමීකරණයෙන් කියැවේ.
මෙහිදී
සියලු පාරිසරික සාධක ඉතා
පරිපූර්ණ (ideal)
තත්වයේ
තිබේ යැයි උපකල්පනය කෙරෙනවා.
එය
ව්යුත්පන්න කරමු.
අයිසොට්රොපික්
සම්ප්රේෂක ඇන්ටනාවකින් ඉහත
ආකාරයට විසුරුවන රේඩියෝ
තරංගයක් තවත් අයිසොට්රොපික්
ඇන්ටනාවකින් ග්රහණය කරන විට
රිසීවිං ඇන්ටනාවට හසුවන ජවය
වන්නේ,
PR
= PT
/(4πR2)
සම්ප්රේෂක
ඇන්ටනාව අයිසොට්රොපික් නොවන
විට, එහි
ගේන් එක ඉහත සමීකරණයට අතුලුත්
කළ යුතුය.
තවද,
ආදායක
ඇන්ටනාවේ effective
aperture අගය
වන AER
= λ2GR/4π
ද ඉහත
සමීකරණයට ඇතුලත් කළ යුතුය
(මෙවිට
ආදායක ඇන්ටනාව අයිසොට්රොපික්
නොවීම හා ඒ හේතුවෙන් ආදායක
ඇන්ටනාවේ ගේන් එක කරලියට
පැමිනීම සිදු වේ).
එවිට ඉහත
සමීකරණය පහත ආකාරයට ලැබේ.
මෙම සමීකරණය
තමයි Friis
equation කියන්නේ.
ඉහත
සමීකරණය තුල FSPL සූත්රයද
ගැබ්ව තිබෙනවා (විශ්ලේෂනය
කර බලන්න). මෙය
ඉතාම ඉතා වටිනා සූත්රයක් වන
අතර, ඇන්ටනා
ක්රියාත්මක වන ආකාරය සමස්ථයක්
වශයෙන් ඉතා හොඳින් මෙම සූත්රය
තුල පැහැදිලි වේ. මෙම
සූත්රයද වලංගු වන්නේ ෆාර්ෆිල්ඩ්
එකට පමණි. ඇන්ටනා
දෙකෙහි පොලරයිසේෂන් වෙනස්
වීම නිසා ඇති වන සංඥා හායනය,
වායුගෝලය
තුලින් රේඩියෝ තරංග ගමන්
කිරීමේදී විවිධ සංසිද්ධි
නිසා ඊට ඇතිවන නොයෙක් හායනයන්
මෙම සමීකරණය සලකා නැත.
එනිසා ඉහත
සූත්රයෙන් ලැබෙන පිළිතුරට
වඩා අඩු ජවයක් බොහෝවිට ආදායක
ඇන්ටනාවේ ජනිත වේවි.

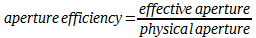


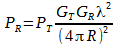
මම මේ ලිපි පෙළ දිගටම කියවගෙන ආපු කෙනෙක් විදිහට ඔබතුමාගේ දැනුම ගැන වගේම පරිත්යාගශීලීත්වය පිළිබදව ලොකු පැහැදීමක් මට ඇතිවුණා දවසක් අහම්බෙන් අන්තර්ජාලයේ ඉද්දි තමයි මට මේ ආධුනික ගුවන්විදුලි ශිල්පය ගැන ඔබතුමාගේ ලිපි පෙළ මුණගැසෙන්නෙ ඇත්තටම කීවොත් ආධුනික ගුවන්විදුලි ශිල්පීන් කියල කොටසක් සිටින බවවත් මම දැනගත්තෙ මෙතනදි තමයි මට පොඩි කාලෙ ඉදන් දැඩි කුතුහලයක් තිබූ (පිස්සුවෙන් වගේ) ස්වයං අධ්යයනයක නිරතවූ සහ උභතෝකෝටිකයක්ව තිබූ කාරණා රැසක් තමයි දුරකතන සන්නිවේදනය ගුවන්විදුලිය රූපවාහිනිය වැනි අංශවල තාක්ෂණික පැත්ත අද මම ඇත්තටම ඉතාම සතුටු වෙනවා මගේ ඒ පිපාසය සංතෘප්ත කරගැනීමට හැකිවීම පිළිබදව එහි පූර්ණ ගරුත්වය ඔබතුමාට හිමිවිය යුතුයි
ReplyDelete:) හොඳින් ඉගෙන ගන්න තවත්. අන්තර්ජාලයේ අද ඕනම දෙයක් ඉගෙනීමට තිබෙනවා. ඒවා පරිශීලනය කරන්න. තවත් අයට ඒ ගැන දැනුවත් කරන්න. ස්වයං අධ්යනය කියන්නේ මිනිසෙකු සතුව තිබිය යුතු අත්යවශ්යම ගුණාංගයකි.
Delete