සන්නිවේදනය හා ආධුනික ගුවන් විදුලිය (Amateur radio) 40

Frequency Reuse

සංඛ්‍යාත නැවත භාවිතය (frequency reuse) යන්නද මල්ටිප්ලෙක්සිං ක්‍රමයක් ලෙස සැලකිය හැකිය. මීට පෙර ඉගෙන ගත් FDM, TDM, CDM යන ශෛලයටම එය Space Division Multiplexing (SDM) ලෙස නම් කිරීම සුදුසුය. මෙහිදී සිදු වන්නේ එකම සංඛ්‍යාතය ස්ථාන කිහිපයකදී එකවිටම භාවිතා කිරීමයි. එහෙත් මෙය කළ හැක්කේ ඒ ස්ථාන අතර යම් අවකාශයක්/වෙන්වීමක් (space) තිබේ නම් පමණි. මෙම ක්‍රමය ඉතාම කාර්යක්ෂම යොදා ගන්නා හොඳම උදාහරණය තමයි සියලුම සෙල්‍යුලර් ජංගම දුරකතන ජාලා.

ඉහත රූපයේ දැක්වෙන්නේ සංඛ්‍යාතයන් 3ක් විශාල ප්‍රදේශයක් (අවශ්‍ය නම් මුලු ලොවම) ආවරණය කරන අන්දමයි. උදාහරණයක් ලෙස f1 නම් කොල පාටින් දක්වා තිබෙන ප්‍රදේශවල භාවිතා වන්නේ එකම සංඛ්‍යාතයයි. එහෙත් එක් කොල පාට පෙදෙසක් තවත් කොල පාට පෙදෙසකින් යම් අවකාශයකින් වෙන් වෙනවා. එලෙස සංඛ්‍යාත 3ක් (හෝ ඊට වැඩි ගණනක්) භාවිතයෙන් යම් භූමියක් ආවරණය කළ හැකි බව පැහැදිලියි නේද?

ඇත්තටම මල්ටිප්ලෙක්සිං ක්‍රමයක් ලෙස එකවර මෙය අපට කල්පනා නොවුණත්, ස්වභාව ධර්මයා විසින් අපට ඉබේම සලසා දී තිබෙන මල්ටිප්ලෙක්සිං ක්‍රමය මෙයයි. ඒකනෙ වෙනත් රටවලින් නිකුත් වන (බොහෝ) රේඩියෝ තරංගවලින් අපට කරදරයක් නැත්තේ. එලෙස බාධා නැති නිසා අපේ රට තුල එම සංඛ්‍යාත යොදා ගෙන සන්නිවේදනය කළ හැකියි. එලෙසම අපේ රටේ එම රේඩියෝ සංඥාද වෙනත් රටවලට යන්නේ නැත.

විශේෂයෙන් සියලු ඉහල සංඛ්‍යාත රේඩියෝ තරංග (HF ට ඉහල සංඛ්‍යාත හෙවත් 30MHz ට ඉහල සංඛ්‍යාත) සඳහා මෙය අනිවාර්යෙන්ම අදාල වේ. HF සංඛ්‍යාත පරාසයේ සංඥා තරංග වායුගෝලයෙන් ඊට ලැබෙන අපූරු සහයෝගය නිසා කිලෝමීටර් දස දහස් ගණන් ඈතට විසුරුවා හැරිය හැකියි (මේ ගැන පසු පාඩමක් ඇත). මේ සඳහා විශාල ජවයක්ද අවශ්‍ය වෙනවා. එසේ වුවත්, එය එසේ ඈතට ගමන් නොකෙරෙන සේද අපට උපක්‍රම යෙදිය හැකියි (ඇන්ටනා සවිකරන විදියෙන් හා ජවය අඩු කිරීමෙන්). ඒ කියන්නේ SDM ක්‍රමය HF සංඛ්‍යාත සඳහාද භාවිතා කළ හැකි බවයි. ඇත්තටම රේඩියෝ සංඥාවල ජවය අවශ්‍ය ප්‍රමාණයට තබා ගැනීම මඟින් ඉතා පහසුවෙන් SDM භාවිතා කළ හැකියි සමස්ථ රේඩියෝ තරංග පරාසය සඳහාම.

එක් උපමාවකින් මේ ක්‍රමය තවත් හොඳට පැහැදිලි කළ හැකියි. එක ළඟ මහා ඝෝෂාවක් සහිත සංගීත සංදර්ශන දෙකක් හෝ කිහිපයක් එකවිට පවත්වන්නට බැහැනෙ. එවිට දෙකෙහිම සංගීතයන් එකතු වී එකම ඝෝෂාවක් වනු ඇත. එහෙත් එම සංගීත සංදර්ශන දෙක වෙනත් ප්‍රදේශ දෙකක පැවැත්විය හැකි නම් (එකෙක ශබ්දය අනෙකට නෑසෙන සේ), කිසිදු ගැටලුවක් ඇති වන්නේ නැහැ. එයම තමයි SDM හිදිත් සිදු වන්නේ. ඒ කියන්නේ සුදුසු පරතරයක් තබා ගන්නවා නම්, මේ ක්‍රමයෙන් අපට හැකියි සීමිත සම්පතක් වන රේඩියෝ සංඛ්‍යාතයන් බොහෝ දෙනෙකුට භාවිතා කළ හැකි ලෙස පරිපාලනය කරන්න. ඇත්තටම, ලෝකයේ සෑම සන්නිවේදනය පද්ධතියක්ම අවශ්‍යයෙන්ම මෙම උපක්‍රමය භාවිතා කරනවා.

මුලදීම අප ඉගෙන ගත්තා සෑම රටකටම සම්පූර්ණ රේඩියෝ සංඛ්‍යාත පරාසයට අයිතයක් තිබෙන බව. එනිසා ඒ ඒ රටයි අවසාන තීරණය ගන්නේ රේඩියෝ සංඛ්‍යාත පරාසයන් කෙසේ තම රට තුල භාවිතා කළ යුතුද කියා. ශ්‍රී ලංකාව වැනි රටක් දූපතක් නිසා අනෙක් රටවලින් තරමක් ඈතින් හුදකලාව සිටින නිසා මේ අයිතිය ඉතා හොඳින් බුක්ති විඳිනවා. එහෙත් එක ගොන්නට තිබෙන රටවලට නම් යම් ගැටලුවක් තිබෙනවා. යම් රටකින් නිකුත් කරන යම් රේඩියෝ සංඛ්‍යාතයක් එම රටේ දේශ සීමාවෙන් නතර වෙන්නේ නැහැනෙ. අහල පහල අනෙක් රටවල් තුලටද ඇතුලු වෙනවා. එනිසා, ඒ ඒ රටවල් අවබෝධතා ගිවිසුම් ආදිය ඇති කර ගන්නවා සංඛ්‍යාතයන් කාටත් සාධාරණ ලෙස භාවිතා කළ හැකි පරිදි. මෙහිදී ITU ආයතනයත් හොඳ රාජකාරියක් සිදු කරනවා ප්‍රශ්න අවම කිරීම සඳහා. මේවා නෛතික රාමු තුල SDM යොදා ගැනීමේදී තිබෙන අභියෝග වන අතර ඉතා හොඳින් එම අභියෝග මේ දක්වා කළමණාකරණය කරගෙන තිබෙන බව පේනවා.

Orthogonal Frequency Division Multiplexing (OFDM)

මෙය FDM හි සුවිශේෂි අවස්ථාවකි. දෙන ලද සංඛ්‍යාත පරාසයක් ඊටත් වඩා පටු සංඛ්‍යාත පරාසයන් ගණනාවකට බෙදනවා (මෙලෙස පටු සංඛ්‍යාත පරාසයකට බෙදන නිසා තමයි FDM ක්‍රමයක් කියා කියන්නේ). සමහරවිට එවන් පටුපරාසයන් සිය ගණනකට හෝ දහස් ගණනකට පමණ බෙදිය හැකිය. එහෙත් එලෙස බෙදන්නේ සුවිශේෂි ගතිලක්ෂණයක් මතු වන ආකාරයටයි. එම ගතිලක්ෂණයට තමයි orthogonal කියා කියන්නේ. මේ ගැන දැන් තරමක් විස්තරාත්මකව බලමු.

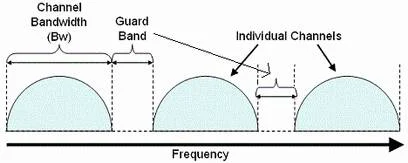
පහත දැක්වෙන්නේ සාමාන්‍ය FDM ක්‍රමයට පටුසංඛ්‍යාත පරාස සාදා ගන්නා හා OFDM ක්‍රමයට පටුසංඛ්‍යාත පරාස සාදා ගන්නා අයුරු පැහැදිලිව දැක්වෙන රූපයකි. සාමාන්‍ය ක්‍රමයේදී එක් එක් සංඥාවන් සඳහා සංඛ්‍යාත පරාස පවරන විට, ඒ අතර යම් හිඩැසක් (guard band) තබනවා. එහෙත් OFDM ක්‍රමයේදී එම හිඩැස නැතිවා පමණක් නොව, එක් එක් සංඥාවලට අදාල සංඛ්‍යාත කොටස් යම් ක්‍රමවත් රටාවකට එක උඩ එක (overlap) වන ආකාරයටයි තබන්නේ.

පරිපථවලට ඉතාම අපහසුයි අහවල් සංඛ්‍යාතයේ සිට අහවල් සංඛ්‍යාතය දක්වා පමණක් සංඛ්‍යාත පරාසයන් නිශ්චිතවම පවතින පරිදි සංඥා සාදන්නට. හැමවිටම සංඥා සංඛ්‍යාත පරාසයෙන් පිටතටත් දුර්වල සංඥා ප්‍රමාණයක් ගමන් කරනවා. සමහර අවස්ථාවලදී එලෙස සංඛ්‍යාත පරාසයෙන් පිටතට විහිදෙන කොටස්වල තිබිය හැකි උපරිම ජව ප්‍රමාණයන් විවිධ රෙගුලාසිවලින් හෝ ප්‍රමිතින් විසින් නියම කරද තිබෙනවා. එසේ වුවත්, එම පිටතට විහිදෙන දුර්වල සංඥා විසින් අනුයාත සංඛ්‍යාතයන්හි පවතින සංඥාවලට බාධා ඇති කළ හැකියි. එය වැලැක්වීමට තමයි සාමාන්‍ය FDM හි හිඩැස් හෙවත් ගාඩ් බෑන්ඩ් තබා තිබෙන්නේ.

තවත් වැදගත් වැදගත් කාරණයක් මෙහිදී කිව යුතුය. ඔබ මීට පෙර ඉගෙන ගත්තා FM ක්‍රමයේදී capture effect කියා සංසිද්ධියක්. එනම්, ප්‍රබල එෆ්එම් සංඥාවක් දුබල එෆ්එම් සංඥාව යටපත් කරදමා එෆ්එම් රිසීවරයෙන් ඇසෙනවා. එම කැප්චර් ආචරණය මෙහිදී අපට වාසියකට හරවා ගත හැකියි. සිතන්න යම් සංඥා දෙකක් FM ක්‍රමයට විසුරුවා හරිනවා කියා එක ළඟ (අනුයාත) සංඛ්‍යාත දෙකක. මෙවිට අපට හැකියි ඉහත ආකාරයේ ගාඩ් බෑන්ඩ් එකක් නැතිව සංඥා සංඛ්‍යාතයන් දෙක යාබදව තබන්නට. මෙවිට, එක් සංඥාවකින් පිටතට විහිදී යන දුර්වල සංඥා කොටසින් අනෙකට එතරම් බාධාවක් නොදැනෙනු ඇති. එහෙත් එය සාර්ථක වන්නේ සංඛ්‍යාත මූර්ජන ක්‍රමයන්හිදි පමණි.

ඉතිං එලෙස ගාඩ් බෑන්ඩ් තබමින් ඈතින් ඈතට පටුපරාසයන් පිහිටුවනවාට වඩා කොටසක් එක උඩ එක වැටෙන පරිදි සකස් කළ විට, ඉන් විශාල සංඛ්‍යාත පරාසයක් ඉතිරි කර ගත හැකියි නේද? එය තමයි OFDM වල තිබෙන ප්‍රමුඛතම වාසිය. ඒ කියන්නේ OFDM හි spectrum efficiency ඉහලය.

මෙලෙස එක් එක් සංඥාවන්ට අදාල සංඛ්‍යාත පරාසයක් එක උඩ එක තබන විට ඉන් අනෙක් සංඥාවන්ට බාධාවක් නොවන්නේදැයි කෙනෙකු ඇසිය හැකිය. එය සාධාරණ ප්‍රශ්නයක් වන අතර, ඊට පිළිතුර බාධාවක් ඇති නොවේ යන්නයි. ඊට හේතුව එක් එක් පරාසයන් එක උඩ එක තිබුණත්, එම පරාසයන් එකිනෙකට orthogonal වේ.

orthogonal යන්න ගණිතයේ හමුවන ලස්සන තේරුමක් තිබෙන වචනයකි. යම් කිසි සාධක/විචල්‍ය/මාන/රාශි දෙකක් ගත් විට, ඉන් එකක අගය අනෙකෙහි අගයෙන් කිසිසේත් ප්‍රකාශ කළ නොහැකියි යන තේරුම ඊට ඇත; එනම් එකක් අනෙකට බලපෑම් ඇති නොකරයි යන තේරුමයි. උදාහරණයක් ලෙස, x හා y යන අක්ෂ දෙක සහිත ඛණ්ඩාංක/ප්‍රස්ථාර තලයක් සලකන්න. එහි ඔබ x තිරස් අක්ෂය දිගේ ඍණ/වම් පැත්තට හෝ ධන/දකුණු පැත්තට කොතරම් දුරක් ගියද ඉන් හැකි වෙන්නේ නැහැ y සිරස් අක්ෂයට බලපෑමක් ඇති කරන්න; එනම් y අගය නියතව පවතිනවා. එලෙසම y අක්ෂය දිගේ කොතරම් විචලනය වුවත්, එය x අක්ෂයේ අගයට කිසිදු බලපෑමක් නැත. එනිසා x හා y අක්ෂ දෙක එකිනෙකට ඕර්තගොනල් වේ. එලෙසම යම් කෙනෙකුගේ හැසිරීම/ක්‍රියාවක් ඔබට කිසිදු බලපෑමක් ඇති නොකරයි නම්, ඔබගේ හැසිරීම/ක්‍රියාවක් ඔහුට/ඇයට කිසිදු බලපෑමක් ඇති නොකරයි නම්, ඔබලා දෙදෙනාත් එකිනෙකාට ඕර්තගොනල් වේ.

ඒ අනුව OFDM හිදි එක් පටුපරාසයක් අනෙක් පටුපරාසයකට “දැනෙන විශාල” බලපෑමක් ඇති නොකරයි (ඇත්තටම කුඩා බලපෑමක් තිබෙන නමුත් එය සමස්ථ ක්‍රියාකාරිත්වයට බලපෑමක් නොවන තරමින් වේ). මෙලෙස ඕර්තගොනල් ලක්ෂණය පැවතීමට සැපරිය යුතු කොන්දේසියක් තිබේ. එනම්,

එක් සංඥාවක ශූන්‍ය අගය තිබෙන (හෙවත් අවසාන) කෙලවර (null) අනෙක් සංඥාවේ උපරිම වන අවස්ථාව (peak) සමග සමපාත විය යුතුය.

පහත රූපයේ රතු පාටින් රවුම් කර තිබෙන්නේ එම ස්ථානයි.

එක් එක් පටුපරාසය subcarriers (උපවාහක) ලෙස හඳුන්වනවා. ඉහත රූපයේ එවැනි සබ්කැරියර් 6ක් ඇඳ තිබෙනවා. ඉතිං, මේ එක් එක් සබ්කැරියර් එක වෙන වෙනම යම් අඩුවේගී සංඥා විසින් මූර්ජනය කරනවා. සාමාන්‍යයෙන් ඩිජිටල් සංඥායි මේ සඳහා යොදා ගැනෙන්නේ. එනිසා අපට කැමති ඕනෑම ඩිජිටල් මූර්ජන ක්‍රමයකින් තනි තනි සබ්කැරියර් මූර්ජනය කිරීම සඳහා යොදා ගත හැකියි. BPSK, QPSK, QAM යන ක්‍රම මේ සඳහා බහුලවම භාවිතා කෙරෙනවා.

OFDM තාක්ෂණය අවස්ථා දෙකක් සඳහා යොදා ගත හැකියි (එනම් පැතිකඩවල්/කෝණ දෙකකින් බැලිය හැකියි).

1. තනි අධිවේගී සංඥාවක්/දත්තයක් සම්ප්‍රේෂණය කිරීමට

2. විවිධ සංඥා/දත්ත කිහිපයක් එකවර සම්ප්‍රේෂණය කිරීමට

තනි අධිවේගී දත්ත සම්ප්‍රේෂනය කිරීමක් සඳහා සාම්ප්‍රාදායික සම්ප්‍රේෂණ ක්‍රමයක් නම් යොදා ගන්නේ එම දත්ත වේගයට ගැලපෙන විශාල බෑන්ඩ්විත් එකක් සහිතව, තනි කැරියර් එකක් සුදුසු මූර්ජන ක්‍රමයක් යොදා ගෙන එය සිදු කරනවා. එහෙත් එහිදී multipath fading, inter-symbol interference වැනි බරපතල ගැටලු කිහිපයකට මුහුන දෙන්නට සිදු වෙනවා. විශේෂයෙන් සන්නිවේදන පද්ධතිය ජංගම නම් එම ගැටලු තවත් බරපතලයි (ඒවා ගැන පසුවට විමසමු). එම ගැටලුවලට හොඳ විසඳුමක් OFDM කියන්නේ. මෙහි එක් තනි කැරියර් එකක් වෙනුවට සබ්කැරියර් විශාල ගණනක් (තුන හතරක සිට දසදහස් ගණනක් දක්වා) භාවිතා කරනවා. එවිට, අධිවේගි දත්තය අඩු වේගී දත්ත කිහිපයකට කඩා එක් එක් සබ්කැරියර් එකකින් වෙන වෙනම ඒවා යවනවා.

මෙලෙස යම් තනි දත්තයක් සබ්කැරියර් ගණනාවක් යොදා ගෙන සම්ප්‍රේෂනය කිරීම multicarrier modulation (MCM) හෝ multicarrier transmission (බහුවාහක සම්ප්‍රේෂණය) ලෙස හැඳින්වෙනවා. OFDM යනු මල්ටිකැරියර් සම්ප්‍රේෂනය සඳහා පෙන්වා දිය හැකි හොඳම උදාහරණයයි. මීට අමතරව තවත් මල්ටිකැරියර් සම්ප්‍රේෂන ක්‍රම තිබේ.

ඉතිං, OFDM යනු මල්ටිප්ලෙක්සිං ක්‍රමයක් වුවත්, ඉහත පෙන්වා දුන් ලෙසට තනි සංඥාවක් යැවීම සඳහා නම් යොදා ගන්නේ එය සාම්ප්‍රදායික අර්ථයෙන් මල්ටිප්ලෙක්සිං එකක් නොවේ නේද මොකද සාම්ප්‍රදායිකව මල්ටිප්ලෙක්සිං එකකින් සිදු කළේ වෙනස් වෙනස් සංඥා කිහිපයක් එකවර යැවීමයි? කෙසේ වෙතත් පරිපථයට නම් එකම සංඥාවේ කොටස්ද නැතිනම් වෙනස් වෙනස් සංඥාද කියා වෙනසක් නැති නිසා, මෙතැනත් තාක්ෂණික ඇසින් බලන විට මල්ටිප්ලෙක්සිං එකක්මයි සිදු වන්නේ. ඇත්තටම අප පෙර ඉගෙන ගත් CDM හා තවත් ක්‍රමවලටට පවා මේ තත්වය පවතිනවා. එනම්, එම ක්‍රම යොදා ගත හැකියි අධිවේගි තනි සංඥාවක් පමණක් සම්ප්‍රේෂණය කිරීමට.

OFDM සාම්ප්‍රදායික මල්ටිප්ලෙක්සිං ක්‍රමයක් ලෙසද යොදා ගත හැකියි. එහිදී වෙනස් වෙනස් සංඥා (අඩුවේගී සංඥා විය යුතුය) කිහිපයක් එකට සම්ප්‍රේෂනය වේ. මෙවිට මල්ටිකැරියර් සම්ප්‍රේෂනය යන වචනය වලංගු නැත (එම වචනය කිව හැක්කේ තනි සංඥාවක් සඳහා පමණි). බලන්න එකම සංසිද්ධිය/ක්‍රියාවලිය වුවත් කෝණ දෙකකින් බලන විට ලොකු වෙනස්කමක් තිබෙනවා.

මෙම විස්තර කියවාගෙන යන අතර අපට වැදගත් කරුණක් මඟ හැරී යනවා. එය මෙහිදී මා ඉස්මතු කරන්නට කැමතියි. මුල්ම පාඩම්වලදී පැවසුවා දත්ත/සංඥා යැවිය හැකි ක්‍රම දෙකක් තිබෙනවා කියා - සීරියල් හා පැරලල්. එහෙත් එහිදී මා පෙන්වා දුන්නා පැරලල් ක්‍රමයට වඩා සීරියල් ක්‍රමය ප්‍රායෝගිකව බහුලව යොදා ගන්නා බවත්. එහෙත් මල්ටිකැරියර් සම්ප්‍රේෂනය යනු පැරලල් සම්ප්‍රේෂන ක්‍රමයක් තමයි මොකද එකම සංඥාවේ කොටස් වෙනස් වෙනස් සබ්කැරියර් හරහා එකවර සම්ප්‍රේෂනය සිදු වෙනවා. ඒ කියන්නේ රේඩියෝ තරංග තාක්ෂණයේදී දැන් නැවත පැරලල් ක්‍රමය ඉදිරියෙට එමින් තිබෙනවා කියන එකයි. පැරලල් ක්‍රමය වයර් සඳහා නුසුදුසු වන්නට ප්‍රධාන හේතුවක් වූයේ වැඩි වයර් ප්‍රමාණයක් වැය වීමයි. එහෙත් රේඩියෝ සංඥා ගත් විට වයර් ගැටලුවක් නැහැනෙ. එය නව ප්‍රවණතාවක්.

ඇත්තටම ඉහත ආකාරයට ඇඳ තිබෙන රූපයේ යම් දෝෂයක් ඇත (මූලික සංකල්පය පැහැදිලි කිරීමට එය කදිම වුවත්). එම රූපයේ පෙන්වා තිබෙන්නේ කැරියර් තරංග පමණි. මෙම කැරියර්වලට සංඥා මූර්ජනය කෙරෙනවානෙ. එවිට එම කැරියර් තරංග හැඩය වෙනස් වෙන බව අප දන්නවා (එහි ප්‍රතිපලයක්නෙ සංඛ්‍යාත පරාසයක් යම් සංඥාවක් සඳහා අවශ්‍ය වීම). OFDM ක්‍රමය ඩිජිටල් ක්‍රමයකි. ඉතිං ඩිජිටල් සංඥා කොටු හැඩැතිය. ෆූරියර් න්‍යාය අනුව, කොටු හැඩයක් සයිනාකාර තරංග සෙට් එකක එකතුවක් ලෙස දැක්විය හැකියිනෙ. එවැනි තරංග සෙට් එකක පවතින ෆන්ඩමන්ටල්/ප්‍රමූලික තරංගය හා එහි උපරිතාන (harmonics) මඟින් ඕර්තගොනල් ලක්ෂණය අහෝසි කිරීමට ඉඩ ඇත. ඒ අනුව, අපට සිදු වෙනවා ඩිජිටල් කොටු තරංගය යම් කිසි විදියකට සකස් කරන්නට ඕර්තගොනල් ලක්ෂණය පවත්වා ගෙන යා හැකි පරිදි. මෙහිදී කරන්නේ කොටු තරංගයක් යම් wave shaping ෆිල්ටරයක් හරහා යවා “sinc signal” එකක් බවට පත් කිරීමයි.

sinc(x) ශ්‍රිතය යනු sin(πx)/πx වේ.

සටහන

සින්ක් ශ්‍රිත දෙකක් ඇත.

1. sin(πx) / πx – normalized sinc function

2. sin (x) / x – unnormalized sinc function

සාමාන්‍ය සයින් ශ්‍රිතය ඇඳ දක්වන විට, එය කදිම සයිනාකාර තරංග හැඩයක් ගන්නවානෙ (විස්තාරය දිගටම එකම උසින් තිබෙන පරිදි).

 

එහෙත් එම සයින් ශ්‍රිතයේ ඇති පරාමිතියෙන් එම ශ්‍රිතය බෙදූ විට (එනම්, sin(x)/x) වටිනා ගුණාංගයක් අපට ලැබේ.

x=0 වන විට, සයින්(0)=0 වේ. ඒ කියන්නේ x=0 විට, සයින්(0)/0 යන්න 0/0 බවට පත්වේ. 0/0 යනු ගණිතයේදී අවලංගු ගණිත ප්‍රකාශයකි. එහෙත් උසස් ගණිත ක්‍රමයක් මාර්ගයෙන් පෙන්විය හැකියි සයින්(0)/0 යන ප්‍රකාශයේ පිළිතුර ලෙස ලැබෙන අගය 1 බව. ඒ කියන්නේ සයින්(x)/x යන්න x=0 අවස්ථාවේදී 1 අගය ගනී.

ඒ සමඟම සයින්(x) යන්නට විවිධ අගයන් ලබා දෙන විට සංඥාව විචලනය වන්නේ ආවර්තිකවනෙ (ඉහත සයිනාකාර තරංග හැඩයට). ඉතිං ක්‍රමයෙන් (ධන හා ඍණ දෙපැත්තෙන්ම) ක්‍රමයෙන් විශාල වන සේ x ට අගයන් ලබා දෙනවානෙ. එලෙස ක්‍රමයෙන් ඉහලට යන අගය සහිත x වලින්ම සයින් ශ්‍රිතය බෙදනවානෙ. ඒ කියන්නේ x අගයන් ඉහලට විචලනය වෙන විට, සයිනාකාර ශ්‍රිතය ක්‍රමයෙන් හීන වී යනවා. 0 අවස්ථාවේදී සිරස් උස/අගය 1වන ලෙසත්, ඍණ හා ධන දෙපසට යන විට විස්තාර අගයන් ක්‍රමයෙන් හීන වෙන පරිදි ඉහත සයින් ප්‍රස්ථාරය නැවත ඇන්ද විට ලැබෙන්නේ පහත ආකාරයේ රූපයකි.

 

.

සින්ක් තරංගයේ මැද ලොකුවට (කන්දක් සේ) කොටසක් (peak) තිබෙන අතර, දෙපසට යන විට සංඥා හැඩය ක්‍රමයෙන් හීන වී යනවා (සියලු තරංග කොටස් එකම උසින් තිබෙන සේ සකස් කළා නම් එය පිරිසිදු සයිනාකාර තරංගයක් බවට පත්වෙනවා).

1 යන බිට් අගයට (එනම් රූපයේ පෙන්වා ඇති පරිදි කොටු තරංගයකට) සුදුසු සින්ක් හැඩය සකසන්නේ ඕර්තගොනල් ලක්ෂණය මතුවන ආකාරයට විය යුතුය. එනම්, සින්ක් තරංගය තිරස් අක්ෂය කපන්නේ අනෙක් සබ්කැරියර් එකේ උපරිම විස්තාර අගය (එනම් අනෙක් සබ්කැරියර් වල කන්ද වැනි ස්ථාන) පවතින අවස්ථාවලයි. දැන් එක් එක් සබ්කැරියර් මෙබඳු සින්ක් සංඥාවලින් මූර්ජනය කළ විට සමස්ථ සංඥා සෙට් එකම පහත ආකාරයට දිස් වේ (පැවතිය හැකි නරකම අවස්ථාව (worse case) වන සෑම සබ්කැරියර් සංඥාවක්ම ඩිජිටල් 1 වන අවස්ථාවකදි).

මෙවිට යම් සංඥාවක (සබ්කැරියර් එකක) සංඥා කොටස් අනුයාත සංඥා/සබ්කැරියර්වලට ඇතුලු වුවත්, අනුයාත සබ්කැරියර්වල උපරිම විස්තාර අගය පවතින අවස්ථාවලදී (peak) අප දැන් සලකා බලන සංඥාවේ ශූන්‍ය අගය (null) සමපාත වනු ඇත (රූපය හොඳින් බලන්න). ඉතිං ෆන්ඩ්මන්ටල් තරංගයේ සංඛ්‍යාතය සුදුසු පරිදි සකස් කළ විට උපරිතාන ඉබේම සැකසෙනවනෙ. එමඟින් ඕර්තගොනල් ලක්ෂණය ඉතාම හොඳින් සුරක්ෂිත වේ.

යම් සංඥාවක් Fourier Transformation (FT) මඟින් ෆන්ඩමන්ටල් තරංගයකුත් එහි උපරිතාන කිහිපයකුත් වශයෙන් ලැබෙනවානෙ. එය අප සාමාන්‍යයෙන් හඳුන්වන්නේ time domain signal එකක් frequency domain එකට පත් කරනවා කියාය. සාමාන්‍ය (ක්‍රමවත් හෝ අක්‍රමවත්) සංඥාවක්/තරංග හැඩයක් කාලයට සාපේක්ෂව ඇඳ දක්වනවා (ඒ කියන්නේ තිරස් අක්ෂයෙන් කාලය දක්වනවා). එනිසයි එම සංඥාව time domain (කාල රාමුවක්) තුල පවතිනවා ලෙස සලකන්නේ. එහෙත් FT කළාට පසුව අපට ලැබෙන්නේ සුපිරිසිදු සයිනාකාර තරංග සෙට් එකක්. එක් සයිනාකාර තරංගයක් තවත් සයිනාකාර තරංගයකට හැඩයෙන් හැමවිටම සමානයි - එහෙත් සංඛ්‍යාතයෙන්, විස්තාරයෙන් වෙනස්. එබැවින් FT කළාට පසුව අපට සංඛ්‍යාත සෙට් එකම ඉතා සරලව එක් එක් සංඛ්‍යාතයේ අගයෙන් සලකා බැලිය හැකියි (ඒ කියන්නේ තිරස් අක්ෂයෙන් සංඛ්‍යාත අගය දක්වනවා). එනිසා දැන් අපට කියන්නට පුලුවන් අර සංඥාව frequency domain (සංඛ්‍යාත රාමුව) තුල නිරූපණය කෙරෙනවා කියා.

ඉතිං, FT මඟින් කරන රාජකාරියට විරුද්ධ රාජකාරිය Inverse Fourier Transformation (IFT) කියා කියනවා. ඉන් සිදු වන්නේ තනි තනි සංඛ්‍යාතවලින් පවතින සංඥා/තරංග රාශියක් තනි time domain signal එකක් බවට පත් කිරීමයි. FT සිදු කරන ආකාර හා ඒ සම්බන්ද ගැඹුරු තත්වයන් පවතින අතර කැමති නම් ඒ ගැනත් ඉගෙන ගත හැකියි.

දැනට FT හා IFT සිදු කරන පහසු ප්‍රචලිත ආකාරය Fast Fourier Transformation (FFT) හා Inverst Fast Fourier Transformation (IFFT) ලෙස හඳුන්වනවා. සාම්ප්‍රදායික FT/IFT ට වඩා අතිවිශාල වේගයකින් FFT/IFFT ක්‍රියාත්මක වේ. FT/IFT ට යමක් කිරීමට පියවර N² ගන්නා අතර, FFT/IFFT ට ඒ සඳහා වැය වෙන්නේ N.log(N) පියවර ගණනකි. උදාහරණයක් වශයෙන් N=100,000 නම්, FT ට 100,000² = 10,000,000,000 වැයවන අතර, FFTට වැය වන්නේ, 100,000.log(100,000) = 100,000x5 = 500,000 කි; එනම් FT ට වඩා FFT 10,000,000,000/500,000 = 20,000 ගුණයක් වේගවත්ය (සලකා බැලූ උදාහරණය වන N=100,000 වන අවස්ථාව සඳහා). බලන්න කොතරම් වේගවත්ද FFT/IFFT? FFT හා IFFT අපට භාවිතා කළ හැකියි OFDM පරිපථවලදී.