තවත් අපූරු ඡන්දයක් නිම විය. එය කරුණු රැසක් නිසා අපූර්ව වේ. සමහරු කියන පරිදි රදලයන්ගේ දේශපාලනයේ අවසානයක් (තාවකාලිකව හෝ) ඉන් සිදු විය. වැඩ කරන ජනයාගේ, නිර්ධන පංතියේ නායකයෙකු හා පක්ෂයක් බලයට පත් වීමද සුවිශේෂී වේ. රටේ මෙතෙක් සිදු වූ සකල විධ අපරාධ, දූෂන, භීෂන සොයා දඩුවම් කරනවා යැයි සමස්ථ රටවැසියා විශ්වාස කරන පාලනයක් ඇති විය. තවද, බහුතර කැමැත්ත නැති (එනම් 43%ක කැමැත්ත ඇති) ජනපතිවරයකු පත් විය. ජවිපෙ නායකයෙක් "තෙරුවන් සරණයි" කියා පැවසීමත් පුදුමය. මේ සියල්ල ලංකා ඉතිහාසයේ පලමු වරට සිදු වූ අපූරු දේශපාලන සංසිද්ධි වේ. මාද විවිධ හේතුන් මත අනුරට විරුද්ධව මෙවර තර්ක විතර්ක, සංවාද විවාද, හා "මඩ" යහමින් ගැසූ තත්වයක් මත වුවද, ඔහු දැන් රටේ ජනපති බැවින් ඔහුට පලමුව සුබ පතමි. ඔහුට විරුද්ධව වැඩ කලත්, මා (කිසිදා) කිසිදු පක්ෂයකට හෝ පුද්ගලයකුට කඩේ ගියේද නැති අතර අඩුම ගණනේ මාගේ ඡන්දය ප්‍රකාශ කිරීමටවත් ඡන්ද පොලට ගියෙ නැත (ජීවිතයේ පලමු වරට ඡන්ද වර්ජනයක). උපතේ සිටම වාමාංශික දේශපාලනය සක්‍රියව යෙදුනු පවුලක හැදී වැඩී, විප්ලවවාදි අදහස්වලින් මෙතෙක් කල් දක්වා සිටි මා පලමු වරට සාම්ප්‍රදායික (කන්සර්වටිව්...
දැන් ප්‍රතිරෝධකයක් හා ධාරිත්‍රකයක් ශ්‍රේණිගතව සම්බන්ධ වන අවස්ථාව සලකමු. මෙය Series RC circuit ලෙස හැඳින්වෙනවා.
මෙහිදීද ප්‍රථමයෙන්ම ස්ථාවර ඩීසී විදුලියක් ගමන් කරන අවස්ථාව බලමු. කැප් එක නිසා පරිපථය හරහා ධාරාවක්/විදුලියක් ගමන් නොකර පරිපථ කොටස අක්‍රිය වේ. විචලනය වන විදුලියක් සහිත විට පමණක් පරිපථය හරහා ධාරාවක් ගලා යයි. උපාංග දෙක ශ්‍රේණිගතව පවතින නිසා ගලා යන්නේ එකම ධාරාවකි. එ් කියන්නේ ධාරිත්‍රකය හරහා යන ධාරාවයි ප්‍රතිරෝධකය හරහා යන ධාරාවයි සමකලාවේ පවතිනවා කියන එක. එහෙත් ඔබ දන්නවා ධාරිත්‍රකයක් හරහා හැමවිටම විභවයට වඩා අංශක 90කින් ධාරාව පෙර ගමන් කරනවා. අවශ්‍ය නම්, එයම ධාරාවට වඩා පිටුපසින් අංශක 90කින් විභවය ගමන් කරනවා කියාත් පැවසිය හැකියිනෙ. ඉතිං මෙම තොරතුරු අපි දැන් පහසුවෙන් තේරුම් ගැනීමට ෆේසර් ඩයග්‍රැම් එකක අඳිමු. IC හා IR සමකලාවේ පවතී. ප්‍රතිරෝධකයක හැමවිටම ධාරාව හා වෝල්ටියතාව සමකලාවේ වේ. එමනිසා VR ද එම අක්ෂයේම නිරූපණය කළ යුතුය. කැප් එකේ ධාරාවට වඩා විභවය 90කින් පිටුපසින් යන නිසා, VC රූපයේ ආකාරයට සිරස්ව පහලට පැත්තට ඇඳිය යුතුය (ඍණ කෝණ රෙෆරන්ස් ලයින් එකේ සිට දක්ෂිණාවර්තවයි අඳින්නෙ).
මෙහි මුලු ධාරාවේ අගය කොපමණද? Parallel RC සර්කිට් එකේදී මෙන්ම මෙහිදිත් එය එකවර පැවසිය නොහැකියි. තවද, මෙහිදී එක් එක් උපාංග දෙපස රැඳෙන වෝල්ටියතාව පහසුවෙන් තීරණය කිරීම කළ නොහැකියි මෙම මුලු ධාරාව දැනගන්නා තෙක්. මුලු ධාරාව දැනගත්තේ නම්, එම ධාරාවෙන් ප්‍රතිරෝධයේ අගය වැඩි කිරීමෙන් ප්‍රතිරෝධකය දෙපස රැඳෙන විභවයද, එම මුලු ධාරාව ධාරිත්‍රකයේ ප්‍රතිභාදක අගය සමග වැඩි කිරීමෙන් ධාරිත්‍රකය දෙපස ඩ්‍රොප් වන විභවයද ගණනය කළ හැකියි. මෙලෙස ලබා ගත් උපාංග දෙකේ විභවයන් පවතින්නේ අංශක 90ක කලා වෙනසකින්ය (ඉහත රූපයේ එය දිස්වේ). මේ අනුව සියල්ලම කිරීමට පරිපථයේ සමක සම්භාදකය සෙවිය යුතුය. ඉහත පරිපථයේ තිබුණේ නිකංම ප්‍රතිරෝධක දෙකක් නම්, ඍජුවම එම ප්‍රතිරෝධ අගයන් දෙක එකතු කිරීමෙන් සමක ප්‍රතිරෝධය ලැබේ, R = R1 + R2 සූත්‍රය අනුව. එහෙත් මෙතැන තිබෙන්නේ ප්‍රතිරෝධකයක් හා ධාරිත්‍රක ප්‍රතිභාදකයක්. මෙවැනි අවස්ථාවක යොදන සූත්‍රය වන්නේ,
Z = R + jX වේ.
මෙහිද j තිබෙන නිසා, පෛතගරස් ප්‍රමේය යොදාගෙනයි එය සුලු කිරීමට සිදු වන්නේ.
Z සොයාගත් පසු, වෝල්ටියතාව එම Z වලින් බෙදා පහසුවෙන්ම ධාරාව ගණනය කළ හැකි වෙනවා. උදාහරණයක් ඇසුරින් මෙය තවදුරටත් ඉගෙන ගමු. පෙර රූපයේ දැක්වෙන පරිපථය අනුව ගණනය කිරීම් කරමු.
පළමුවෙන්ම ධාරිත්‍රකයේ ප්‍රතිභාදක අගය සෙවිය යුතුය. එය ඕම් 160කි. දැන් සම්භාදකය සොයමු.
Z2 = R2 + X2 → Z2 = 10002 + 1602 → Z = 1013 ohm
ඒ අනුව, ගලන මුලු ධාරාව වන්නේ V/Z = 10/1013 = 0.0099A හෙවත් 9.9mA වේ.
එවිට, VR = R x I = 1000 x 0.0099 = 9.9V හා VC = X x I = 160 x 0.0099 = 1.6V වේ.
ඉහත ගණනය කිරීම් ආසන්න අගයන්ට සන්නිකර්ෂණය කර තිබේ. ඉහත ධාරිත්‍රක හා ප්‍රතිරෝධක විභවයන් දෙක එකතු කළ විට භාහිර සැපයුම් වෝල්ටියතාවට සමාන වන්නේ නැත. ඊට හේතුව කලාව වෙනස් වීම වේ. සම්භාදකය ගණනය කිරීමට පයිතගරස් ප්‍රමේයය යෙදුවා මෙන්ම, භාහිර වෝල්ටියතාව සෙවීමටද එය යෙදීමට සිදු වේ. සූත්‍රයක් ලෙස එය පහත දැක්වේ.
VS2 = VR2 + VC2 (VS = VR - jVC)
ඉහත සූත්‍රයට ඉහත ලබා ගත් අගයන් ආදේශ කර ගණනය කර බලන්න නිවැරදි පිළිතුර ලැබේවි (VS2 = (9.9)2 + (1.6)2 → VS = 9.972; එම අගය 10ට ඉතාම ආසන්නය). මෙම නව වෝල්ටියතාව ධාරාවට වඩා යම් කලාවකින් පිටුපසින් සිටී. එය සෙවීමට සුපුරුදු tan-1(X/R) යන සූත්‍රය යොදන්න. එවිට කලා කෝණය -9 පමණ වේ. ඒ කියන්නේ ෆේසර් ඩයග්‍රැම් එකේ x අක්ෂයට යටින් අංශක 9ක් සහිතව ඉරකින් මෙය ඇඳිය හැකියි. 9 යනු කුඩා කෝණයකි. ඇත්තටම කෝණයේ විශාලත්වය ගැන හැඟීමක් ගත හැකියි X හා R අගයන් දෙක දෙස බලන විට. X අගයට වඩා R අගය වැඩි වන විට, කෝණය කුඩා වේ.
ධාරිත්‍රකයක් හා ප්‍රතිරෝධකයක් එකතු වී සාදන සම්භාදකය ගැන හොඳ දැනුමක් දැන් ඔබ සතුව තිබෙනවා. මීට අමතරව, ප්‍රතිරෝධකයක් හා ඉන්ඩක්ටන්ස් එකක් එකතු වීමෙන්ද සම්භාදකයක් සාදනවා (මේ ගැන ඉන්ඩක්ටර් පාඩම්වල ඉදිරියෙදි හමු වේ). තවද, ප්‍රතිරෝධක, ධාරිත්‍රක, හා ඉන්ඩක්ටර් යන උපාංග තුනම එකතු වීත් සම්භාදක සාදනවා.
සම්භාදකය ගණනය කිරීම තරමක් අමුතු වුවත්, එය ගණනය කළ පසු රෙසිස්ටර් මෙන් ඒවා සැලකිය හැකියි. එවිට, සම්භාදක දෙකක් එකිනෙකට සම්බන්ධව ඇති විට, එහි සමක සම්භාදක අගය ප්‍රතිරෝධකවල යෙදූ සූත්‍රම යොදාගෙන ගණනය කළ හැකියි. එනම්, ශ්‍රේණිගතව සම්බන්ධිත සම්භාදක දෙකක්
Z = Z1 + Z2
යන සූත්‍රයෙන්ද, සමාන්තරගතව සම්බන්ධිත සම්භාදක දෙකක්
1/Z = 1/Z1 + 1/Z2
යන සූත්‍රයෙන්ද ගණනය කළ හැකියි.
ෆිල්ටර්
ප්‍රතිරෝධකයක් හා ධාරිත්‍රකයක් යොදාගෙන අපට විවිධාකාරයේ filter සාදාගත හැකියි. ඒ කියන්නේ මෙයත් RC circuit (හෝ CR circuit) එකක්. ෆිල්ටර් එකක් යනු ඉලෙක්ට්‍රොනික්ස්වල නැතිවම බැරි පරිපථ වර්ගයකි. ෆිල්ටර් එකක් යනු කුමක්ද? ලබා දෙන (ඉන්පුට්) විදුලි සංඥාවක පවතින විවිධ සංඛ්‍යාතවලින් යුතු තරංග අතරින් තෝරාගත් සංඛ්‍යාතයන්ගෙන් යුතු තරංග පමණක් පිටතට ලබා දීම (අවුට්පුට්) ෆිල්ටරයකින් සිදු කෙරේ.සටහන
ඉලෙක්ට්‍රොනික්ස්වල පමණක් නොවේ ෆිල්ටර් භාවිතා වන්නේ. කුස්සියෙ තිබෙන වතුර ෆිල්ටරය ගැන සිතන්න. ඊට උඩින් වතුර දැමූ විට, එහි රොඩු, බැක්ටීරියා ආදිය ඉවත් කර ඔබට අවශ්‍ය කරපු පිරිසිදු වතුර පිටතට ලබා දෙනවා. තේ සෑදීමේදී භාවිතා කරන තේ ගොට්ට/පෙරනයද එලෙසමයි. වැලි හැලීමට යොදා ගන්නා රයිසිය, පිටි හැලීමට ලබා ගන්නා පෙරනයද ආදී ලෙස මේ සෑම ෆිල්ටර් එකකින්ම කරන රාජකාරිය එකමයි. වාහනවල, ෆ්‍රිජ්වල, පටක රෝපනයේදී, විද්‍යාගාරවල ආදී නොයෙකුත් තැන්වල මෙලෙස විවිධාකාරයේ ෆිල්ටර් භාවිතා කෙරෙනවා. මේ ආදි ලෙස විවිධ අවස්ථාවන් සඳහා අප ෆිල්ටර් භාවිතා කිරීමෙන් ආරක්ෂාව හා කොලිටිය (වැඩි ගුණාත්මකබවක්) අපේක්ෂා කරනවා නේද? උදාහරණයක් ලෙස, වතුර ෆිල්ටරය සලකන්න. ඉන් අපිරිසිදු දෑ ඉවත් කර පිරිසිදු වතුර පිටතට ලබා දීමෙන් ඔබව ලෙඩ රෝගවලින් ආරක්ෂා කරනවා. තේ හදන විට යොදාගන්නා තේ පෙරනය සලකන්න. එයින් වෙන්නේ ඔබට රොඩු බොඩු නැති තේ එකක් ලබා දීමයි; එනම් තේ එකේ කොලිටිය වැඩි කිරීමයි.
ඉලෙක්ට්‍රොන්ක් ෆිල්ටර්වල ප්‍රයෝජනයත් එයයි. එනම්, සර්කිට් එකේ ක්‍රියාකාරිත්වයේ ඉහල ගුණාත්මක බවක් ලබා ගැනීම හෝ සර්කිට් එකේ ඇති උපාංගවල ආරක්ෂාව ඉන් තහවුරු වේ. උදාහරණයක් ලෙස සිතන්න මිනිස් කන ගැන. දළ වශයෙන් මිනිසෙකුට හර්ට්ස් 20 සිට 20,000 දක්වා වූ සංඛ්‍යාතයන්ගෙන් යුතු ශබ්ද/කම්පන තමයි ඇසෙන්නේ. මෙම පරාසයේ සවුන්ඩ් audible sound (ශ්‍රව්‍ය සංඛ්‍යාත ශබ්ද) ලෙස හැඳින්වෙනවා. හර්ට්ස් 20,000ට වැඩි සංඛ්‍යාත ultrasound (අතිධ්වනි) ලෙසද, හර්ට්ස් 20ට අඩු සංඛ්‍යාත infrasound (අවධ්වනි) ලෙස නම් කෙරෙනවා. ඔබේ කනට ඇසෙන්නේ ශ්‍රව්‍ය සංඛ්‍යාත ශබ්ද වුවද පරිසරයේ ඉහත පරාස තුනටම අයත් වන සේ කම්පන ඇති වෙනවා. උදාරහණයක් ලෙස, ඔබ මේසයට තට්ටු කළ විට, ඉන් ශබ්දයක් ඇති වෙනවානෙ. ඒ ඔබට දැනුනේ ශ්‍රව්‍ය පරාසයේ කම්පනයයි. ඔබට සංවේදනය නොවන පරාසයේ කම්පනද එහි පවතිනවා. තවද, තල්මසුන්, වවුලන් ආදී සතුන්ද අතිධ්වනි තරංග යොදාගන්නවා (හරියට අප ශ්‍රව්‍ය සංඛ්‍යාත තරංග යොදා ගන්නවා වාගේ). ඉතිං මයික් එකකින් එවැනි ශබ්දයක් පරිපථයක් තුලට ගෙන ස්පීකර් එකකින් පිට කරන විට, ඔබේ කනට ඇසෙන හා නොඇසෙන පුලුල් පරාසයක් කම්පන පවතිනවා. එලෙස ඉන්ෆ්‍රාසවුන්ඩ් හා අල්ට්‍රාසවුන්ඩ් තිබීම කරුණු කිහිපයක් නිසාම ප්‍රශ්න ඇති කරනවා. එකක් නම්, කනට නොඇසෙන එම ශබ්ද වෙනුවෙන් පරිපථයෙන් ශක්තියක් බොරුවට වැය වේ. තවද, ස්පීකරයට සමහරවිට එම කම්පන හානිකර වේ. ඔබ දැක ඇති සමහර ස්පීකර්වල කෝන් එක ඉරිතලා හෝ පුපුරා තිබෙනවා. ඊට එක් හේතුවක් තමයි, ස්පීකරයට ඔරොත්තු නොදෙන සංඛ්‍යාතවල කම්පන එහි ඇති වීම. සාමාන්‍යයෙන් ස්පීකර් එකක් සාදන්නේ සීමිත සංඛ්‍යාත පරාසයක කම්පන/ශබ්ද පිටකිරීම සඳහායි. මේ හේතු නිසා, එවැනි ශ්‍රව්‍ය සංඛ්‍යාතවලට පරිභාහිරව පවතින අනවශ්‍ය හා හානිකර සංඛ්‍යාත ෆිල්ටර් කළ යුතුයි නේද? එය අත්‍යවශ්‍ය දෙයක්. ඒ විතරක් නොවේ, ස්පීකර් ගණනාවක් හරහා හයිෆයි සවුන්ඩ් එකක් ලබා ගන්නේද ක්‍රොස්ඕවර් ලෙස හැඳින්වෙන ෆිල්ටර් සර්කිට් භාවිතා කරමින්ය. මේ ආදි ලෙස, බොහෝමයක් අවස්ථා සඳහා අපට ෆිල්ටර් අත්‍යවශ්‍ය වේ.
ඉහත උදාහරණයම තවදුරටත් විස්තර කරන්නට කැමතියි. අල්ට්‍රාසවුන්ඩ් මිනිස් කනට ඇසෙන්නේ නැති වුවද, එ් මඟින් විවිධ වටිනා කාර්යන් සිදු කරගන්නවා. මව් කුස තුළ සිටින දරුවකුගේ ප්‍රතිබිම්භ ලබා ගැනීම (ultrasound scan) , පොලොව යට පවතින මැනික්/පුරාවස්තු ආදී දේවල් “ස්කෑන්” කිරීමට, මුහුදු ආරක්ෂාවට/මාලු ඇල්ලීමට ආදිය යොදා ගන්නා සෝනාර්වල, යන්ත්‍රෝපකරණ පිරිසිදු කිරීම (ultrasound cleaning) ආදී බොහෝ යෙදුම් ඊට උදාහරණ වේ. මේ සෑම අවස්ථාවකදීම අතිධ්වනි යොදා ගත්තත් අපේ කනට ඒවා නොඇසෙන නිසා කිසිදු “කරච්චලයක්” නැත. මේ සියලු අවස්ථාවල අප ෆිල්ටර් යොදා ගන්නවා අතිධ්වනි හැර අනෙක් පහළ සංඛ්‍යාත කම්පන සියල්ල කපා දැමීමටත්.
ඔබ දන්නවා ඉලෙක්ට්‍රොනික්ස් වැඩ කරන්නේ විදුලි සංඥා සමගයි. විදුලි සංඥා විවිධ හැඩයන්ගෙන් යුක්තයි. මීට පෙරත් සඳහන් කළ ආකාරයට ඕනෑම අක්‍රමවත් තරංග හැඩයක් යනු විවිධ සංඛ්‍යාතයන්ගෙන් හා විස්තාරයන්ගෙන් යුතු සයිනාකාර තරංග රාශියක එකතුවක්. ඉතිං මෙවැනි අක්‍රමවත් සංකීර්ණ තරංග ස්වරූපයක් ගමන් කරන විට, ඉහත සඳහන් කළ ආකාරයේ හේතුන් නිසා, අපට අවශ්‍ය වෙනවා එම සංකීර්ණ හා සංයුක්ත (combined) තරංගවලින් ඔබට අවශ්‍ය (එනම් ඔබ විසින් තීරණය කරන) සංඛ්‍යාතවලට පමණක් ගමන් කරවීමට සලස්වන්නට. උදාහරණයක් ලෙස සිතමු හර්ට්ස් 100 සිට 1000 දක්වා වූ පරාසයක වූ සංඛ්‍යාතවලින් යුත් සංයුක්ත තරංගයකින් හර්ට්ස් 500ට වැඩි සංඛ්‍යාතවලට පමණක් ගමන් කිරීමට සලස්වා ඊට අඩු සංඛ්‍යාත බ්ලොක් කිරීමට අවශ්‍යයි කියා. මෙය තමයි ෆිල්ටර් එකකින් සිදු කරන්නේ.
ඇත්තටම ප්‍රධාන ෆිල්ටර් 2ක් ඇත.
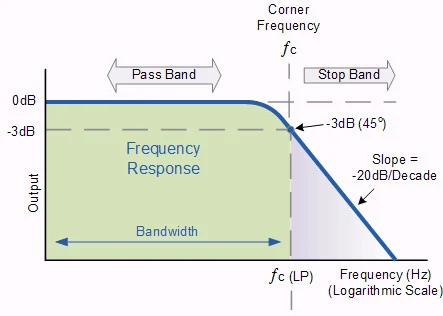
1. යම් කිසි තෝරාගත් සංඛ්‍යාතයකට පහළ සංඛ්‍යාතයන්ට පමණක් ගමන් කිරීමට සලස්වන ෆිල්ටර් එක. මෙහිදී එම තෝරාගත් සංඛ්‍යාතයට ඉහලින් ඇති සංඛ්‍යාතයන් බ්ලොක් කෙරේ. මෙය Low Pass Filter (LPF) ලෙසයි හැඳින්වෙන්නේ. තෝරාගත් සංඛ්‍යාතය cut-off frequency හෝ corner frequency (fC) ලෙස හැඳින්වේ. ෆිල්ටර් නොවී ගමන් කිරීමට සලස්වන සංඛ්‍යාත පරාසය passband ලෙසද, ෆිල්ටර් කර දමන සංඛ්‍යාත පරාසය stopband ලෙසද නම් කෙරෙනවා. ඒ අනුව පහත LPF හි පාස්බෑන්ඩ් එක වන්නේ fC සංඛ්‍යාතයට වම් අත පැත්තට ඇති සංඛ්‍යාත පරාසය වන අතර, fC ට දකුණු අත පැත්තෙන් ඇති සංඛ්‍යාත පරාසය ස්ටොප්බෑන්ඩ් වේ.
2. යම් කිසි තෝරාගත් සංඛ්‍යාතයකට (cut-off frequency) වඩා ඉහල සංඛ්‍යාතයන්ට පමණක් ගමන් කිරීමට සලස්වන ෆිල්ටර් එක. මෙහිදී එම තෝරාගත් සංඛ්‍යාතයට පහල සංඛ්‍යාතයන් බ්ලොක් කෙරේ. High Pass Filter (HPF) ලෙස මෙය හැඳින්වේ.
ඉහත ප්‍රධාන ෆිල්ටර් දෙක එකට යොදා ගනිමින් සංයුක්ත ෆිල්ටර් සාදා ගත හැකියි. ඒ අතරින් ප්‍රධානතම සංයුක්ත ෆිල්ටර් වර්ග 2ක් තිබේ.
1. යම් කිසි තෝරාගත් සංඛ්‍යාත අගයන් දෙකක් අතර සංඛ්‍යාත කලාපයකට (frequency band) පමණක් ගමන් කිරීමට සලස්වන ෆිල්ටර් එක. මෙහිදී මෙම තෝරාගත් සංඛ්‍යාත පරාසයෙන් පිට සියලු සංඛ්‍යාත බ්ලොක් කෙරේ. මෙය Band Pass Filter (BPF) ලෙස හැඳින් වේ. කට්-ඕෆ් සංඛ්‍යාත දෙකෙන් පහල අගය සහිත එක lower cut-off frequency ලෙසද, ඉහල අගය සහිත සංඛ්‍යාතය upper cut-off frequency ලෙසද හැඳින්වෙනවා. අවම හා උපරිම කට්-ඕෆ් සංඛ්‍යාත දෙක අතර පවතින සංඛ්‍යාත පරාසය bandwidth ලෙස හැඳින්වෙනවා.
2. යම් කිසි තෝරාගත් සංඛ්‍යාත අගයන් දෙකක් (ලෝවර් කට්-ඕෆ් හා අපර් කට්-ඕෆ් සංඛ්‍යාත දෙක) අතර සංඛ්‍යාත කලාපයක් බ්ලොක් කර, ඉන් පිට සියලු සංඛ්‍යාතයන්ට ගමන් කිරීමට සලස්වන ෆිල්ටර් එක. මෙය Notch Filter ලෙස හැඳින්වේ. මෙයම Band Notch Filter, Band Rejection Filter, Band Elimination Filter, Band Stop Filter යන නම්වලිනුත් හැඳින්වේ (notch, rejection, elimination, stop යන ඉංග්‍රිසි වචන සියල්ලම මෙහිදී එකම තේරුම ලබාදේ).
මීටත් අමතරව, විවිධ ලෙස සරල ෆිල්ටර් කොටස් එකතු කරමින් ඉන්පුට් කරන සංඛ්‍යාත පරාසය තුළ විවිධ විවිධ තැන්වල පවතින සංඛ්‍යාතවලට පමණක් යෑමට හැකි පරිදි ෆිල්ටර් වර්ග සාදා ගත හැකියි.
පහත රූපය බලන්න. මෙය ඔබ ඉහත දුටු විභව බෙදුම් පරිපථයක් නේද? ඔව්. එහෙත් දැන් අප මෙම පරිපථය පෙරනයක් (ෆිල්ටරයක්) ලෙසයි යොදා ගන්නේ. මෙය පෙරනයක් ලෙස ක්‍රියා කරන්නේ කෙසේදැයි දැන් සොයා බලමු.
මෙහි ඉන්පුට් අග්‍ර දෙකට විවිධ සංඛ්‍යාතයන්ගෙන් යුතු විදුලි සංඥාවක් යොමු කළේ යැයි සිතන්න. එම එක් එක් සංඛ්‍යාතයන්ගෙන් යුතු තරංගයන්ට ධාරිත්‍රකය මීට පෙර ඔබ උගත් පරිදි විවිධ ප්‍රතිබාධක අගයන් දක්වනවා. සංඛ්‍යාතය ඉහල යන විට, ප්‍රතිබාධකය පහල යනවා. උදාහරණයක් ලෙස, මේ අතරින් හර්ට්ස් 100 සංඥාවට ඉහත රූපයේ ධාරිත්‍රකයෙන් ඕම් 1600 ක ප්‍රතිබාධයක් අැති කරනවා. එවිට එම හර්ට්ස් 100 සංඥාව සඳහා ධාරිත්‍රකය හා ප්‍රතිරෝධකය සාදන විභව බෙදුමෙන් ඉන්පුට් වෝල්ටියතාව 1600:100 හෙවත් 16:1 අනුපාතයට බෙදෙනවා. ඒ කියන්නේ එම හර්ට්ස් 100 සංඥාවෙන් අවුට්පුට් වන්නේ ඉන්පුට් කරපු වෝල්ටියතාවෙන් (1/(16+1) =) 1/17 ක (හෙවත් 0.059ක) කුඩා ප්‍රමාණයක් හෙවත් ප්‍රතිශතයක් ලෙස (0.059 x 100% =) 5.9% කි. ඒ කියන්නේ ඉන්පුට් කරපු සංඥාවේ විශාලත්වයෙන් (වෝල්ට් ගණනින්) (100-5.9=) 94.1% ක ප්‍රමාණයක් කැපී ගොස් (ඇටෙනුවේට්) ඇත. ප්‍රායෝගිකව මෙය තමයි සංඥාවක් ෆිල්ටර් වෙනවා යනුවෙන් පවසන්නේ (සෛද්ධාන්තිකව නම් 100%කින් ෆිල්ටර් වෙනවා කිව්වත්, ප්‍රායෝගිකව ඉහත පෙන්වා දුන් පරිදි යම් ප්‍රතිශතයක් දක්වා තමයි ෆිල්ටර් වීම සිදු වෙන්නේ). දැන් හර්ට්ස් 10000 ක සංඥාවක් ගෙන බලමු. එවිට එම ධාරිත්‍රකයෙන් ඕම් 16ක ප්‍රතිබාධකයක් ඇති කරනවා. එය 16:100 ක හෙවත් 4:25 අනුපාතයකින් විභව බෙදුම ඇති කරනවා. ඒ කියන්නේ අවුට්පුට් වෝල්ටියතාව ඉන්පුට් වෝල්ටියතාවෙන් (25/(25+4) =) 25/29 ක් හෙවත් ප්‍රතිශතයක් ලෙස 86%ක්. ඒ කියන්නේ මෙහිදී ෆිල්ටර් වී ඇත්තේ 14%ක් වැනි කුඩා ප්‍රමාණයක්. මෙහිදී ඉන්පුට් වෝල්ටියතාව එතරම් අඩු නොකර අවුට්පුට් වෝල්ටියතාව ලෙස ලබා දෙනවා නේද? ඒ කියන්නේ හර්ට්ස් 100000 සංඥාව එච්චර ෆිල්ටර් වෙලා නැහැ. ඉහත ෆිල්ටරයෙන් සංඛ්‍යාතය වැඩි වේගෙන යන විට, ෆිල්ටර් වීම ක්‍රමයෙන් අඩු වේගෙන යනවා.
මේ ආකාරයට එක් එක් සංඛ්‍යාතයක් සඳහා අවශ්‍ය නම් ඉහත ආකාරයට ඉන්පුට් වෝල්ටියතාවට සාපේක්ෂව අවුට්පුට් වෝල්ටියතාවේ ප්‍රතිශතය ගණනය කළ හැකියි. තනි තනි සංඛ්‍යාතය සඳහා එකින් එක ගණනය කර දැක්වීම ප්‍රායෝගිකව කළ නොහැකි බැවින්, එය ප්‍රස්ථාරයක් ලෙස පහත ආකාරයට දැක්විය හැකියි. හර්ට්ස් 100 සිට 10000 දක්වා සංඛ්‍යාත පරාසය තුළ ඕම් 100 රෙසිස්ටරයක් හා මයික්‍රොෆැරඩ් 1ක කැප් එකක් සහිත ඉහත රූපයේ පෙන්නුම් කළ පරිපථයේ එක් එක් සංඛ්‍යාතයෙන් ෆිල්ටර්වන ප්‍රමාණය ප්‍රතිශතයක් වශයෙන් මෙම ප්‍රස්ථාරය සකසා ඇත.
ඉහත විස්තරය අනුවත් ප්‍රස්ථාරය අනුවත් ඔබට දැන් යම් ගැටලුවක් ඇති විය හැකියි. එනම්, ෆිල්ටර් වීමේදී අවශ්‍ය සංඛ්‍යාතය 100% ක්ම ෆිල්ටර් වෙන්නේ නැත. එවිට, ඔබ ඇසිය යුතුයි ඉන්පුට් කරපු සංඥාවෙන් සියයට කොච්චරක් දක්වා අඩු වූ විටද ෆිල්ටර් වීමක් ලෙස සලකන්නේ කියා. එය හොඳ ප්‍රශ්නයක්. ලබා දුන් සංඥාවේ ජවයෙන් (හෝ ශක්තියෙන්) 50%ක් දක්වා අඩු වූ විට “සම්මතයක් වශයෙන්” ෆිල්ටර් වීමක් ලෙස සැලකේ. ඒ කියන්නේ ඉන්පුට් කරපු සංඥාවේ ජවයෙන් හරි අඩක් දක්වා අඩු වූයේ නම්, එතැන ෆිල්ටර් වීමක් සිදු වූයේ යැයි කියයි. ප්‍රායෝගිකව ඇත්ත වශයෙන්ම ඊට අඩු ප්‍රතිශතයන්ගෙන් හා වැඩි ප්‍රතිශතයන්ගෙන්ද ෆිල්ටර් වීම සිදු වෙන බවද මතක තබා ගන්න. ඉහත ප්‍රස්ථාරයේ ඉතා විශාල සංඛ්‍යාත පරාසයක් තුල (දළ වශයෙන් හර්ට්ස් 1600 සිට ඉහලට; එනම් 1600Hz තැන සිට දකුණු අත පැත්තට) සංඥාව ඇටෙනුවේට් වෙන්නේ ඉතා ස්වල්ප වශයෙනි. සාමාන්‍යයෙන් එම ස්වල්පයත් අප නොසලකා හැර, අප සඳහන් කරනවා එම පාස්බෑන්ඩ් එක ෆිල්ටර් වී නොමැති බව. එලෙසම ස්ටොප්බෑන්ඩ් එක සීඝ්‍රයෙන් ෆිල්ටර් වෙන බවද පේනවා (ඉහත ප්‍රස්ථාරයේ දකුණු පැත්තට වන්නට තිබෙන වක්‍ර කොටස).
හොඳින් සිහිතබා ගන්න මා ඉහත ඡේදයේ ෆිල්ටර් වීම අර්ථ දැක්වූයේ ජවය මත මිසක් ධාරාව හෝ වෝල්ටියතාව මත නොවේ. එය හිතාමතා කළ දෙයකි. ජවයෙන් කොතරම් ප්‍රමාණයක් ඇටෙනුවේට් වෙනවාද යන්නයි අර්ථ දැක්වීමට ගෙන තිබෙන්නේ. එහෙත් අපට හැකියි ජවය වෙනුවට වෝල්ටියතාව හෝ ධාරාව වුවත් යොදා ගන්නට ෆිල්ටර් වන ප්‍රමාණයන්/ප්‍රතිශතයන් දැක්වීම සඳහා. මේ ගැන මොහොතකින් විස්තර කෙරේ.
ඉහත ප්‍රස්ථාරය බැලූ විට එක් එක් සංඛ්‍යාතයන් ෆිල්ටර් වන්නේ විවිධ ප්‍රතිශතවලින් බව පැහැදිලිව පෙනේ. ප්‍රතිශත දක්වන y අක්ෂයේ 50% ස්ථානය තමයි සම්මතය අනුව ෆිල්ටර් වීම ආරම්භ කරන තැන. ඉහත high pass filter එකට අදාල ප්‍රස්ථාරයේ එම 50% ප්‍රතිශතයේ සිට පහල ප්‍රතිශතයන් පෙන්වන සියලු සංඛ්‍යාත ෆිල්ටර් වන බවත්, එම ප්‍රතිශතයේ සිට ඉහල ප්‍රතිශතයන් පෙන්වන සියලු සංඛ්‍යාත ෆිල්ටර් නොවන බවද සැලකිය යුතුයි. එසේ සැලකීම සම්මතයයි.
සටහන
ෆිල්ටර් ගැන කතා කිරීමෙදිත් තව බොහෝ තැන්වලත් හමුවන වචනයකි/සංකල්පයකි ඩෙසිබෙල්. ඇත්තටම ඩෙසිබෙල් යනු එතරම් වැදගත් නොවන වැඩ අවුල් කරන සංකල්පයකි. එහෙත් බොහෝ දෙනා මෙය බහුලව යොදා ගන්නා නිසා එය ගැන ඉගෙන ගත යුතුය. මොකක්ද මේ ඩෙසිබෙල්? එය ගණිතයේදී හමුවන දර්ශක හා ලඝු යන ගණිත සංකල්ප උපයෝගී කර ගනිමින් සාදා ඇත. යම් රාශියක අනුපාත සඳහන් කරන විට මෙය නිතරම යෙදේ. ඉලෙක්ට්‍රොනික්ස්හිදි, වෝල්ටියතාව අසවල් ප්‍රමාණයකින් වර්ධන වූවා, ධාරාව අසවල් ප්‍රමාණයකින් ඇටෙනුවේට් වූවා, ජවය අසවල් අනුපාතයෙන් පිට කරනවා ආදී ලෙස, සලකා බලනු ලබන රාශියේ අනුපාතයක් ගැන කතා කරන විට මෙය යෙදිය හැකියි.
බෙල් (Bel) යන්න පහත පොදු ක්‍රමයට අර්ථ දැක්විය හැකියි.
බෙල් ගණන = ලඝු10(රාශියේ යම් අගයක්/එම රාශියේම තවත් අගයක්)
එනම්, වෝල්ට් හෝ ධාරාව හෝ ජවය හෝ පීඩනය, ශබ්දයේ සැර ආදී වෙනත් රාශියක හෝ අගයන් දෙකක් සංසන්දනය කළ යුතු විට, එම අගයන් දෙකේ අනුපාතය හෙවත් එක් අගයක් අනෙක් අගයෙන් බෙදා, එම ලැබෙන අගයෙහි දහය පාදයේ ලඝු ගත් විට ලැබෙන්නේ බෙල් යන ඒකකයෙන් දක්වන අනුපාතයයි. උදාහරණයක් ලෙස, යම් ඈම්ප් එකකට ඉන්පුට් කරන සංඥාවේ ජවය මිලිවොට් 1ක් නම් හා ඉන් අවුට්පුට් කරන ජවය වොට් 10ක් නම්, එහි ජවය වර්ධනය කරපු ප්‍රමාණය 10W/0.001W = 10000 වේ. එකම රාශියක බෙදීමක් යනු අනුපාතයකි; අනුපාතයකට ඒකක නැත (මොකද හරයේ හා ලවයේ පවතින එකම ඒකක දෙක එකිනෙකට කැපෙන නිසා). එහෙත් බෙල් අනුපාතවලදී "බෙල්" යන ඒකකය අප කෘත්‍රිමව යොදනවා. නිකංම ඉලක්කමක්/අනුපාත අගයක් කියනවාට වඩා යම් ඒකකයක නමක් සහිතව කියන විට, එය අසන/කියවන කෙනාට "බෙල්" යන ඒකක නාමය ඇසෙන විට, එය යම් අනුපාතයක් බව ඉබේම සිහි වෙනවා. ඒ අනුව, මෙම වර්ධන ප්‍රමාණය බෙල් ඒකකයෙන්ද කිව හැකියි. ඉහත අර්ථ දැක්වීම අනුව,
වර්ධනයේ බෙල් ගණන = ලඝු10(10W/0.001W) = ලඝු10 (10000) = 4 Bel වේ.
Bel යන නම ටෙලිෆෝනය මුල්වරට සොයා ගත් ඇලෙක්සැනඩර් ග්‍රැහැම් බෙල් යන සුප්‍රකට නිර්මාණකරුවාට ගෞරව පිණිස යොදා ඇත. Bel යන්නට කෙටි සංඛේතය B වේ. ඒ අනුව 4Bel යන්න 4B ලෙස ලිවිය හැකියි.
ප්‍රධාන මුල් ඒකකය ඉහත විස්තර කළ පරිදි බෙල් වුවත්, ප්‍රායෝගික තලයේදී බෙල් වෙනුවට බෙල් එකකින් දහයෙන් පංගුව වන ඩෙසිබෙල් තමයි භාවිතා කෙරෙන්නෙ. (ඔබ දන්නවා deci යන්න “දහයෙන් පංගුව” යන තේරුම සහිතයි හරියට kilo යන්නට 1000 යන තේරුම පවතිනවා වාගේ). ඒ කියන්නේ
ඩෙසිබෙල් 10 = බෙල් 1
මේ අනුව ඉහත ඈම්ප් එකේ වර්ධනය ඩෙසිබෙල් 40කි. බෙල්/ඩෙසිබෙල් ගණනය කරන ඉහත සරල ලඝු සූත්‍රයේ හරයට වඩා ලවයේ අගය වැඩි වූ විට ලැබෙන්නේ ධණ අගයක් වන අතර, හරයට වඩා ලවයේ අගය අඩු වූ විට ඍණ අගයක් ලැබේ. උදාහරණයක් ලෙස යම් පරිපථ කොටසකින් ඉන්පුට් කරන ජවයෙන් දහයෙන් එක් පංගුවක් නම් අවුට්පුට් කරන්නේ, එහි ඩෙසිබෙල් ගණන ගණනය කරමු.
ඩෙසිබෙල් ගණන = 10ලඝු10 (1/10) = 10ලඝු10(10-1) = 10(-1) = -10 වේ.
එය -10dB ලෙස ලිවිය යුතුය. බෙල්/ඩෙසිබෙල් ගණනය කිරීමට අත්‍යවශ්‍ය වන්නේ අදාල රාශියේ අනුපාතයයි. ඉහත උදාහරණයේ "දහයෙන් එක් පංගුවක්" ලෙස දී ඇත්තේ එම අනුපාතයයි. එය 10:1 යන අනුපාතයයි ("10ක් දුන් විට 1ක් පිට කෙරේ”). ඊට පෙර ඈම්ප් උදාහරණයේදී කෙලින්ම අනුපාතය නොව වෙන වෙනම නිත්‍ය අගයන් (වොට් 10 හා මිලිවොට් 1 ලෙස) තමයි ලබා දී තිබුණේ. එම නිත්‍ය අගයන් පහසුවෙන්ම අපට 0.001:10 හෙවත් 1:10000 ලෙස අනුපාතයක් වශයෙන් සාදා ගත හැකියි. ඒ කියන්නේ කෙලින්ම අනුපාතය දී තිබුණත් නිත්‍ය අගයන් දෙක වෙන වෙනම දී තිබුණත් අපට බෙල්/ඩෙසිබෙල් ගණනය කළ හැකියි.
විදුලිය/ඉලෙක්ට්‍රොනික්ස් ක්ෂේත්‍රයේ පමණක් නොව, වෙනත් ක්ෂේත්‍රවලත් ඩෙසිබෙල් ක්‍රමය බහුලවම යොදා ගන්නවා. උදාහරණයක් ලෙස, ශබ්දයක සැර අඩු වැඩි වීම දැක්වීමටද ඩෙසිබෙල් යොදා ගන්නවා. ශබ්දයක් දෙගුණයකින් වැඩි වීම ඩෙසිබල් 3කින් වැඩි කිරීමකි; ශබ්දයෙන් හරි අඩක් දක්වා සැර අඩු කිරීම ඩෙසිබල් 3කින් අඩු කිරීමකි.
වැඩි වීමක් ධණ ඩෙසිබල් අගයකිනුත් අඩු වීමක් ඍණ ඩෙසිබල් අගයකිනුත් නිරූපණය කෙරෙනවා. එවිට, යම් පරිපථයකින් ශබ්දයේ හඬ -6dB කින් වෙනස් කළා කී විට, ඉන් කියන්නේ එම ශබ්දය හතර ගුණයකින් අඩු කළා කියන එකයි. එම පරිපථයෙන් +3dB කින් වෙනස් කළා කී විට, ඉන් කියන්නේ ශබ්දය දෙගුණයකින් වැඩි කළා කියන එකයි.
විදුලියේදීද ඩෙසිබල් විවිධාකාරයෙන් භාවිතා කරනවා. අතිශය බහුතරයක් අවස්ථාවලදී එය යොදා ගන්නේ විදුලි ජවයන් (වොට්වලින් මනින) දෙකක හෝ විභවයන් (වෝල්ට්වලින් මනින) දෙකක අනුපාත සමගයි. ජවයන් (ශක්ති) දෙකක අනුපාතය මැනීමයි නිවැරදි සම්මත ක්‍රමය. උදාහරණයක් ලෙස, යම් පරිපථ කොටසකට ලැබෙන ජවයෙන් කොතරම් කොටසක් අවුට්පුට් වෙනවාද යන්න දැක්විය හැකියි. එවිට එය "ජව අනුපාතයකි" (power ratio).
Power ratio (dB) = 10 log10(POUT/PIN)
ශක්තිය හෝ ජවය යනු අදිශ රාශියකි. එය කුමන ස්වරූපයෙන් පැවතියත් කුමන ස්‍වරූපවලින් උත්සර්ජනය වුවත් කුමන ස්ථානවලින් එම උත්සර්ජනය සිදු වුවත්, ජවය වෙනස් නොවේ. තවත් ලෙසකින් කියතොත් භාහිර සාධක වෙනස් වුවත් ජවය වෙනස් නොවේ. එනිසයි ජවය අනුපාත සම්මතයක් ලෙස භාවිතා කරන්නෙ. එහෙත් හැමවිටම ජවය යන රාශිය සමග වැඩ කිරීම ඉලෙක්ට්‍රොනික්ස්වල පහසු හෝ ප්‍රායෝගික නැත. සිතා බලන්න පරිපථ සමග වැඩකරන ඔබ වැඩිපුරම කතා කරන්නේ වොට් (ජවය) ගැනද විභවය (වෝල්ට්) ගැනද? සම්මතයක් ලෙස ඩෙසිබෙල් අර්ථ දක්වා තිබෙන්නේ ජවය පදනම් කරගෙනයි. ඊට හේතුව ජවය භාහිර සාධක මත වෙනස් නොවීම බව ඉහත සඳහන් කළා. එහෙත් ජවය = (වෝල්ටියතාව)2/ප්‍රතිරෝධය නිසා, ඉහත සූත්‍රය පහත ආකාරයටද ලිවිය හැකියි නේද?
මෙහි RO යනු අවුට්පුට් කොටසේ ප්‍රතිරෝධය හෙවත් output resistance වේ. RI යනු input resistance වේ. මෙම සූත්‍රය පහසුවෙන් සුලු කළ නොහැකියි. එහෙත් එක කොන්දේසියක් මත මෙම සූත්‍රය සරල කළ හැකියි. එනම්, අවුට්පුට් රෙසිස්ටන්ස් = ඉන්පුට් රෙසිස්ටන්ස් නම්, එම සූත්‍රය පහත ආකාරයට සරල වේ.
power (dB) = 10log10 (VO2/VI2) → 10log10(VO/VI)2 → 20log10(VO/VI)
මෙතැන් සිට එය ජව අනුපාතයක් ලෙස නොව විභව අනුපාතයක් ලෙසයි පෙනෙන්නේ. එහෙත් ඇත්තටම එය තවමත් ජව අනුපාතයම තමයි. මෙම සූත්‍රයේ ඇති වාසිය තමයි, නිතරම භාවිතා කෙරෙන විභවය ඇසුරින් එය පැවතීම. එහෙත් එහි අවාසිය නම්, සමහරුන් එම සූත්‍රය වැරදියට තේරුම් ගැනීමයි. එම වැරැද්ද දෙයාකාරයකින් සිදු වෙනවා.
පළමු වැරැද්ද වන්නේ ඉහත කොන්දේසිය අමතක කිරීමයි. බොහෝ අවස්ථා තිබෙනවා එම කොන්දේසිය සපුරන්නේ නැති. එවැනි අවස්ථාවල මෙම සූත්‍රය යෙදිය නොහැකියි. එවිට වඩා නිවැරදි ජව සූත්‍රය භාවිතා කරන්න.
දෙවැනි වැරැද්ද මීට වඩා සියුම්ය. ඔබ ඩෙසිබෙල් ගැන පැහැදිලි කිරීම හොඳින් තේරුම් ගත්තා නම් පෙනේවි එය නිකංම අනුපාතයක් බව. ඒ කියන්නේ ඔබට අවශ්‍ය ඕනෑම රාශියක් ගෙන එහි අවස්ථා හෝ අගයන් දෙකක් සලකා බැලීමයි ඉන් කරන්නේ. එම අගයන් දෙක ඉන් සංසන්දනය කිරීමකුයි සිදු වන්නේ. ඉතිං එලෙස සංසන්දනය කරන රාශිය ඔබට කැමැති ඕනෑම එකක් විය හැකියි. එය පීඩනය, උෂ්ණත්වය, ශබ්දයේ සැර, විදුලි ධාරාව, ජවය, විදුලි වෝල්ටියතාව ආදී ඕනෑම එකක් විය හැකියි. ඒ අනුව අපට යම් වෝල්ටියතා දෙකක් පහත ආකාරයට පොදු ඩෙසිබෙල් සූත්‍රය ඇසුරින් සංසන්දනය කළ හැකියි නේද?
Voltage ratio (dB) = 10log10(voltageIN/voltageOUT)
ඔව්. එසේ කළ හැකියි. නැවතත් මා කියන්නම් මෙහිදී කර තිබෙන්නේ ඩෙසිබෙල් පොදු සූත්‍රය වෝල්ටියතා දෙකක් සැසඳීමට යොදා ගැනීමයි. හරියටම මෙයම තමයි අප ජව දෙකක් සැසඳීමට යොදා ගත්තෙත්. එහෙත් ඕනෑම දෙයක් කළ හැකි පමණින් එය සම්මතයක් වන්නේ නැත. උදාහරණයක් ලෙස, ඔබට පුලුවන් ඔබ විසින්ම සාදාගත් ඒකකයකින් දුරවල් මනින්නට. ඔබ එලෙස නිර්මාණය කළ දුර මනින ඒකකය ඔබේ නාසයේ දිග හෝ ඔබේ කටේ පළල විය හැකියි. එහෙත් එම ඒකකය සම්මතයක් නොවේ; සම්මතය ලෙස ගෙන ඇත්තේ මීටරයයි. මෙලෙසම විදුලිය සම්බන්ධව ජව අනුපාතය සම්මතයක් වුවත් වෝල්ටියතා අනුපාතය සම්මතයක් නොවේ. ඉතිං මීට පෙර පෙන්වා දුන් පරිදි සම්මතයට ගැලපෙන අයුරින් වෝල්ටියතා ඩෙසිබෙල් අනුපාතය අර්ථ දැක්විය හැකියි (ඒ කියපු කොන්දේසියට යටත්ව). එම සූත්‍රයේ 10 වෙනුවට 20 පැමිණියේ මෙම සම්මතයට අනුකූල වීමක් ලෙසයි (ලඝු රීතින්ට අනුව). ඔබට පෙනෙනවා ඇති සම්මතය අනුව වෝල්ටියතා අනුපාතයේ ඩෙසිබෙල් අගය හා සම්මතය නොවූ එහෙත් පොදු බෙල් අර්ථ දැක්වීම අනුව වෝල්ටියතා අනුපාතයේ ඩෙසිබෙල් අගය යන දෙක අතර පවතින වෙනස්කම.
දහයේ පාදයේ ලඝු ගෙන ඇති නිසා, බෙල් අගය එක බැගින් වැඩි වන්නේ දහයේ ගුණාකාරවලිනි. යම් අගයක දස ගුණයක වැඩි වීමක් බෙල් එකකින් වැඩි වීමකි; සිය ගුණයක වැඩි වීමක් බෙල් දෙකක වැඩි වීමකි; දහස් ගුණයක වැඩි වීමක් බෙල් තුනක වැඩි වීමකි; ආදී වශයෙනි. අඩු වීම ගැනද එලෙසම සිතන්න. දහස් ගුණයක අඩු වීමක් බෙල් තුනක අඩු වීමකි. බෙල් වෙනුවට ඩෙසිබෙල් යොදා ගන්නේ නම්, එම බෙල් අගයන් දහයෙන් ගුණ කර කියන්න. බෙල් තුනක් යනු ඩෙසිබෙල් 30කි; බෙල් 2.3ක් යනු ඩෙසිබෙල් 23කි. බෙල්/ඩෙසිබෙල් සමග වැඩ කටයුතු කිරීමට ලඝු ගැන දැනීමක් ඔබට තිබිය යුතුයි.
ලඝු(1) හැමවිටම 0 වන අතර, ලඝු(10) අගය 1 වේ. ඒ කියන්නේ 1ත් 10ත් අතර පවතින ලඝු/බෙල් අගයන් දශම සංඛ්‍යා වේ. පහත දැක්වෙන්නේ 1ත් 10ත් අතර සංඛ්‍යාවල බෙල් අගයන්ය. බිංදුවේ ලඝු නැත (ඇත්තටම බිංදුවේ ලඝු සෙවිය නොහැකි වීම ඩෙසිබෙල් ක්‍රමයේද දුර්වලතාවක් හැටියට ඉබේම පත් වේ).
| සංඛ්‍යාව | බෙල් අගය | ඩෙසිබෙල් අගය | සංඛ්‍යාව | බෙල් අගය | ඩෙසිබෙල් අගය |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 6 | 0.78 | 7.8 |
| 2 | 0.30 | 3 | 7 | 0.85 | 8.5 |
| 3 | 0.48 | 4.8 | 8 | 0.90 | 9 |
| 4 | 0.60 | 6 | 9 | 0.95 | 9.5 |
| 5 | 0.7 | 7 | 10 | 1.00 | 10 |
ඉහත වගුව අනුව 2 හි ඩෙසිබෙල් අගය 3 වේ. මේ නිසා තමයි, සංඥාවක් දෙගුණයකින් වැඩිවන විට එය ඩෙසිබෙල් 3කින් වැඩි වෙනවා කියාද, සංඥාවක් දෙගුණයකින් අඩුවන විට හෙවත් සංඥාව හරි අඩකින් අඩුවන විට, එය ඩෙසිබෙල් 3කින් අඩු වෙනවා කියා කියන්නේ. මෙම ඩෙසිබෙල් 3 අගය ෆිල්ටර් හා වෙනත් බොහෝ තැන්වල මතු වේ.
සාමාන්‍යයෙන් බෙල්/ඩෙසිබෙල් ගණනය කිරීමේ සූත්‍රයේ ඇති භාග සංඛ්‍යාවේ හරයට හා ලවයට විවිධ අගයන් අදේශ කළ හැකියි (එනම්, හරය හා ලවය යන දෙකම විචල්‍ය වේ). එහෙත් සමහර අවස්ථා තිබෙනවා හරයට විවිධ අගයන් ආදේශ නොකර ඊට නිශ්චිත අගයක් ලියා දක්වන. මෙම නිශ්චිත අගය "දර්ශීය අගය" (reference value) ලෙස හැඳින්වෙනවා. ලවය තිබෙන්නේ විවිධ අගයන් දැමිය හැකි විචල්‍යයක් ලෙසයි. මෙවැනි අවස්ථාවක් සාමාන්‍ය අනුපාතයක් ලෙසම ගණන් ගත නොහැකියි. එවිට, එම අනුපාතය තේරුම්ගත යුත්තේ "හරයේ අගය මෙන් කී ගුණයක් ලවයේ තිබෙනවාද" යනුවෙනුයි. එවිට, මෙවැනි අනුපාතයක් නිකංම dB යනුවෙන් නොදක්වා දර්ශීය අගය හැඟවීමට යම් ඉංග්‍රිසි අකුරක් හෝ අකුරු කිහිපයක් dB ට පසුව යොදනවා. dBV, dBuV, dBmV, dBm, dBJ, dBi, dBW ආදී ලෙස මෙවැනි ඒකක රාශියක්ම පවතී. උදාහරණයක් ලෙස, dBW යනු හරයේ වොට් 1ද ලවයේ තවත් වොට් ගණනක් පවතින ලෙසට ගත් ඩෙසිබෙල්ය. එනම්,
වේ.
එලෙසම, dBm යනු හරයේ දර්ශීය අගය මිලිවොට් 1ක් ඇති විටයි. එනම්,
වේ.
මෙලෙසම,
ප්‍රායෝගිකව පරිපථ නිර්මාණය කරන විට හා ඒවා විශ්ලේෂණය කරන විට, විවිධ ඩෙසිබෙල් අනුපාත ගැන හොඳ දැනුමක් ඔබට ලැබේවි.
මේ අනුව ඉහත විභව බෙදුමක් ලෙස පෙනුන පරිපථය හයිපාස් ෆිල්ටරයක් ලෙස ක්‍රියා කරනවා නේද? දැන් බලමු ඔබට අවශ්‍ය කරන සංඛ්‍යාතයට අනුව හයිපාස් ෆිල්ටර් සර්කිට් එකක් සාදන විදිය. පරිපථයේ තිබෙන්නේ ධාරිත්‍රකයක් හා ප්‍රතිරෝධකයක් පමණි. එය ඉහත රූපයේ ආකාරයට සම්බන්ධ කෙරේ. එහෙත් බොහෝ අවස්ථාවල අප එම ෆිල්ටර් සර්කිට් එකම පහත රූපයේ ආකාරයට අඳිනවා. ඉහත රූපය හා පහත රූපය විදුලිමය වශයෙන් සැලකූ විට එක සමානයි. එහෙත් ඉහත විදියට එය ඇන්ද විට, එය විභව බෙදුමක් ලෙස එකවරම ඇසට පෙනේ; පහත රූපයේ ආකාරයට එය ඇන්ද විට ෆිල්ටර් එකක් ලෙස එකවරම ඇසට පෙනෙනවා.
දැන් ඔබ තීරණය කළ යුතුයි ෆිල්ටර් කළ යුතු කට්-ඕෆ් සංඛ්‍යාතය. එම සංඛ්‍යාතය අගය මත තමයි උපාංග අගයන් තීරණය කරන්නේ. එම සංඛ්‍යාතය පොදුවේ fc ලෙස සටහන් කරමු. මෙම කට්-ඕෆ් සංඛ්‍යාතයේදී ධාරිත්‍රකයේ ප්‍රතිබාධක අගයට ප්‍රතිරෝධකයේ අගය සමාන විය යුතුයි. ඉතිං, මෙම සංඛ්‍යාතය X = 1/( 2πfC) යන සූත්‍රයට යොදන්න. එවිට C = 1/ X ( 2πfc) වේ. එවිට, යම් X අගයක් (ඕම් වලින්) මෙම සූත්‍රයට ආදේශ කළ විට, ඔබ යෙදිය යුතු කැප් එකේ අගය ලැබෙනවා.
ඔබ ලබා දිය යුතු X අගය කුමක්ද? එය තීරණය වන්නේ මෙම ෆිල්ටර් පරිපථය සම්බන්ධ වන අනෙක් පරිපථ කොටස් මතය. සර්කිට් ලෝඩිං සිදු නොවන අයුරින් තමයි X අගය තීරණය කරන්නේ (සර්කිට් ලෝඩිං ගැන මීට පෙර සාකච්ඡා කර තිබේ). ෆිල්ටර් එකක් වෙනත් සුදුසු පරිපථයකට සම්බන්ධ නොකරන්නේ නම් එම ෆිල්ටරයකින් වැඩක් නැහැනෙ. ඉතිං මෙම ෆිල්ටරයට සංඥාව ලබා දෙන මයික් එක හෝ වෙනත් පරිපථ කොටසක් (ඉන්පුට් සෙක්ෂන්) මෙන්ම, මෙම ෆිල්ටර් එකෙන් පසුව එම ෆිල්ටර් කරපු සංඥා ලබා ගන්නා වර්ධකය වැනි තවත් පරිපථ කොටසක් (අවුට්පුට් සෙක්ෂන්) තිබෙනවා. සර්කිට් ලෝඩිං සිදු නොවීමට නම්, ඉන්පුට් සෙක්ෂන් එකේ ප්‍රතිරෝධය මෙන් දස ගුණයක ප්‍රතිරෝධයක් අවම වශයෙන් මෙම ෆිල්ටර් එක සතුව තිබිය යුතුයි. එලෙසම, අවුට්පුට් සෙක්ෂන් එකෙහි ප්‍රතිරෝධයෙන් අවම වශයෙන් දහයෙන් එකක අගයක ෆිල්ටර් එකේ රෙසිස්ටන්ස් එක පැවතිය යුතුයි. උදාහරණයක් ලෙස ඉන්පුට් සෙක්ෂන් එකේ ප්‍රතිරෝධය ඕම් 100 නම් හා අවුට්පුට් සෙක්ෂන් එකේ ප්‍රතිරෝධය කිලෝඕම් 100 නම්, ෆිල්ටර් එකේ ප්‍රතිරෝධය කිලෝඕම් 1 සිට කිලෝඕම් 10 දක්වා පරාසය තුළ පැවතිය යුතුයි.
ඉහත පරාසය තුල පවතින කිලෝඕම් 4 ලෙස ගත්තා යැයි සිතමු. ඒ කියන්නේ ෆිල්ටර් එකේ මුලු ඕම් ගණන කිලෝඕම් 4 විය යුතුයි. ඒ කියන්නේ ඉහත X අගයට දැමිය යුතු අගය කිලෝඕම් 4ද? නැත. එම කිලෝඕම් 4 යනු ධාරිත්‍රකයේ ප්‍රතිබාධකය හා ප්‍රතිරෝධකය යන දෙකෙහිම ශ්‍රේණිගත සමක අගයයි. කට්-ඕෆ් සංඛ්‍යාතයේදී ප්‍රතිබාධකය හා ප්‍රතිරෝධකය සමාන වේ. ඒ කියන්නේ ඉහත කිලෝඕම් 4 දෙකට බෙදිය යුතුයි. එසේ ලැබෙන කිලෝඕම් 2 තමයි X ට ආදේශ කළ යුත්තේ.
ඉහත ගණනය කරන ක්‍රියාවලිය උදාහරණයක් ආශ්‍රයෙන් පියවරින් පියවර පහත ආකාරයට දක්වන්නම්. ඉහත හයිපාස් ෆිල්ටර් සර්කිට් එකේ කට්-ඕෆ් සංඛ්‍යාතය කිලෝහර්ට්ස් 1 යැයි සිතමු. එම ෆිල්ටර් පරිපථයට සම්බන්ධ කර තිබෙන ඉන්පුට් සෙක්ෂන් එකේ ප්‍රතිරෝධය ඕම් 100ද, අවුට්පුට් සෙක්ෂන් එක කිලෝඕම් 100 යැයිද සිතමු. දැන් එම පරිපථයට යෙදිය යුතු ධාරිත්‍රකයේ හා ප්‍රතිරෝධකයේ අගයන් සොයමු.
1. ෆිල්ටර් එකේ මුලු ඕම් ගණන “ඉන්පුට් සෙක්ෂන් ප්‍රතිරෝධය” මෙන් දස ගුණයක් හෙවත් ඕම් 1000 සහ “අවුට්පුට් සෙක්ෂන් ප්‍රතිරෝධය” මෙන් දහයෙන් එක් ගුණයක් හෙවත් කිලෝඕම් 10 අතර පැවතිය යුතුය.
2. ඉහත 1k-10k යන රෙසිස්ටන්ස් රේන්ජ් එකෙන් කිලෝඕම් 4ක අගය තෝරාගමු.
3. මෙම අගයෙන් හරි අඩක් හෙවත් කිලෝඕම් 2ක අගයක් සහිත ප්‍රතිරෝධකයක් තමයි එම පරිපථයට යෙදිය යුත්තේ. (තවද, ප්‍රතිබාධකයේ අගයද කිලෝඕම් 2 වේ).
4. X = 1/( 2πfC) යන සූත්‍රයට, සංඛ්‍යාතයේ හා ප්‍රතිබාධකයේ අගයන් ආදේශ කර C සොයා ගන්න. එවිට,
C = 1/(2000)x(2)x(3.1416)x(1000) = 0.8uF වේ.
දැන් ඔබ ෆිල්ටර් එකේ ධාරිත්‍රකයේ හා ප්‍රතිරෝධකයේ අගයන් දෙක සොයා ගත්තා. පියවරින් පියවර ඔබ ඉගෙන ගත්තා ඉතාමත්ම නිවැරදිව HPF එකක් සාදන අයුරු. ෆිල්ටර් ගැන තවත් විස්තර කිහිපයක් උගත යුතුය. LPF සමග ඒවා ඉගෙන ගමු. දැන් අප බලමු ලෝ පාස් ෆිල්ටර් එකක් සාදන විදිය. මෙහිදී කරන්නේ ඉහත ෆිල්ටර් එකේ උපාංග දෙක මාරු කර තැබීමයි. පහසුවෙන්ම ඔබට දැන් වැටහෙනවා ඇති මෙයත් ඔබ පෙර උගත් තවත් විභව බෙදුම් පරිපථයක් බව.
මෙම පරිපථයද ඉහත HPF විග්‍රහ කළ අයුරින්ම සිදු කර බලන්න. කට්-ඕෆ් සංඛ්‍යාතය ඔබ තීරණය කරන්න. අනෙක් අගයන්ද ඉහත පෙන්වා දුන් පරිදි තර්ක කර ලබා ගන්න. උදාහරණයක් බලමු. කට්-ඕෆ් සංඛ්‍යාතය කිලෝහර්ට්ස් 1 නම්, ඉන්පුට් සෙක්ෂන් එක ඕම් 10 නම් හා අවුට්පුට් සෙක්ෂන් එක කිලෝඕම් 10 නම්, ධාරිත්‍රකයේ හා ප්‍රතිරෝධකයේ අගය සොයන්න. පියවරින් පියවර එය කරමු.
1. ෆිල්ටර් එකේ මුලු/සමක ඕම් ගණන ඕම් 100ත් ඕම් 1000ත් අතර විය යුතුය. මෙම පරාසයෙන් ඕම් 800 තෝරාගමු.
2. එවිට, ඉන් හරි අඩක් වන ඕම් 400ක අගයක් තමයි ප්‍රතිරෝධයට තිබිය යුත්තේ.
3. X = 1/( 2πfC) සූත්‍රය අනුව, ධාරිත්‍රකයේ අගය වන්නේ,
C = 1/( 2πfX) = 1/(2 x 3.1416 x 1000 x 400) = 4uF වේ.
ඉහත ගණනය කළ උදාහරණයේ LPF එකේ ප්‍රස්ථාරය පහත දැක්වේ.
කට්-ඕෆ් සංඛ්‍යාතයෙන් අනෙක් පස කොටස බෑවුමක් සහිතව පෙන්වයි. මෙම බෑවුම roll-off ලෙස හැඳින් වෙනවා. මෙම රෝල්-ඕෆ් එක (හෙවත් බෑවුම) වැඩි වන තරමට ෆිල්ටරය හොඳය. කට්-ඕෆ් සංඛ්‍යාතයේදී ඉන්පුට් සංඥාවේ ජවයෙන් හරි අඩක් පමණයි අවුට්පුට් ජවය ලෙස පවතින්නේ (එලෙසනේ මුලින් අප ෆිල්ටර් වීම අර්ථ දැක්වූවෙත්). ඒ කියන්නේ සංඥාවෙන් අඩක් හායනය වී පවතී. අඩක් අඩුවීම -3dB ලෙස දැක්වෙනවා (ඩෙසිබල් අංකන ක්‍රමයෙන්).
මෙම බෑවුම එකපාරටම සිරස්ව පිහිටිය හැකි නම්, එය තමයි ලෝකයේ තිබිය හැකි ඉස්තරම්ම ෆිල්ටරය. එහෙත් ප්‍රායෝගිකව එවැනි ෆිල්ටර් සෑදිය නොහැකියි. යම් සංඛ්‍යාත පරාසයක් පුරාවට ක්‍රමයෙන් බෑවුම් වන ලෙසයි සෑම ෆිල්ටරයක්ම තිබෙන්නේ. එහෙත් බෑවුම (slope) වැඩි කළ හැකියි. මෙම බෑවුමේ අගය මනින හා දක්වන ක්‍රමයක් ඇත. එය "ඩිකේඩ් එකකට ඩෙසිබල්" (decibels per decade – dB/decade) හෝ "ඔක්ටේව් එකකට ඩෙසිබල්" (decibels per octave – dB/octave) යන ක්‍රම දෙකෙන් එකකින් දැක්වේ. ඩිකේඩ් එකක් යනු, යම් සංඛ්‍යාතයක් ගත් විට, එම සංඛ්‍යාතයත් එම සංඛ්‍යාතයේ දසගුණය පෙන්වන සංඛ්‍යාතයත් අතර සංඛ්‍යාත පරාසයයි. උදාහරණයක් ලෙස, හර්ට්ස් 200 සංඛ්‍යාතය ගමු. එවිට එම හර්ට්ස් 200ට අදාල ඩිකේඩ් එක වනුයේ හර්ට්ස් 200 සිට හර්ට්ස් 2000 දක්වා මුලු සංඛ්‍යාත පරාසයයි. එලෙසම හර්ට්ස් 4ට අදාල ඩිකේඩ් එක වනුයේ 4-40Hz සංඛ්‍යාත පරාසයයි. එලෙසම ඔක්ටේව් එකක් යනු සලකනු ලබන යම් සංඛ්‍යාතයකුත් එහි දෙගුණයක සංඛ්‍යාතයත් අතර පවතින මුලු සංඛ්‍යාත පරාසයයි. උදාහරණයක් ලෙස හර්ට්ස් 200 ගමු. ඊට අදාල ඔක්ටේව් එක වනුයේ හර්ට්ස් 200 සිට හර්ට්ස් 400 දක්වා සංඛ්‍යාත පරාසයයි. එලෙසම හර්ට්ස් 4ට අදාල ඔක්ටේව් එක වනුයේ හර්ට්ස් 4 සිට හර්ට්ස් 8 දක්වා සංඛ්‍යාත පරාසයයි.
සටහන
විද්‍යාව/ගණිතය ගැන අවබෝධයක් තිබෙන අය දන්නවා dec යන උපසර්ගයේ තේරුම "දස" යන්න බව. ඒ අනුව decade යන්නෙහි සාමාන්‍ය ඉංග්‍රිසි තේරුම වසර 10 හෙවත් දශකය යන්නයි. ඉතිං ඉහත ඩිකේඩ් යන්න පහසුවෙන් නමින්ම කියවෙන පරිදි තේරුම් ගත හැකියි. එහෙත් ප්‍රශ්නය තිබෙන්නේ ඔක්ටේව් එක සමගයි. oct යන උපසර්ගයේ තේරුම "අට" යන්නයි. ඉතිං ඉහතදී ඔක්ටේව් එකේ අට ගුණය වෙනුවට දෙගුණයක් යන තේරුම ලැබුණේ කෙලෙසද? මීට සරල පිළිතුරක් තිබෙන්නේ.
ඔක්ටේව් යන්න වැඩිපුරම භාවිතා වූයේ සංගීත විෂයෙහිය. ඔබ දන්නවා සංගීතයේ මූලික ස්වර 7ක් තිබෙන බව. ඉංදියානු ක්‍රමය අනුව එම ස්වර සප්තකය ස, රි, ග, ම, ප, ධ, නි ලෙසද බටහිර ක්‍රමය අනුව එම ස්වර සප්තකයම C, D, E, F, G, A, B ලෙස දැක්වෙනවා (ඉංදියානු ස ස්වරය ඉංග්‍රිසි C ස්වරයට සමානය). මේ සෑම ස්වරයක් සඳහාම නිශ්චිත සංඛ්‍යාතයක් තිබෙනවා. උදාහරණයක් ලෙස C (middle C හෙවත් C4) සඳහා හිමි සංඛ්‍යාතය වන්නේ 261Hz වේ. ස්වර ඉදිරියට යන විට සංඛ්‍යාතය ක්‍රමයෙන් වැඩි වෙනවා. ඒ අනුව A (middle A හෙවත් A4) ස්වරයේ සංඛ්‍යාතය 440Hz වේ. අදාල ස්වර සප්තකයේ අවසාන ස්වරයට ගිය පසු නැවතත් හමුවන්නේද C ස්වරයයි. එහෙත් මෙය මීට පෙර හමු වූ C නොවේ. මෙම අලුත් C යනු පරණ C එකේ සංඛ්‍යාතය මෙන් දෙගුණයයි. එය C5 ලෙස හැඳින්වේ (මොකද මීට පෙර තිබූ C ස්වරය C4 නිසා). ඒ කියන්නේ C වලින් පටන්ගෙන ස්වර 7ම කියා ඊළඟට හමුවන අටවැනි ස්වරය වන්නේ සංඛ්‍යාතය දෙගුණ වී ඇති C ස්වරයයි. එතැන් සිට නැවතත් සුපුරුදු ස්වර පෙළ (සරිගමපදනි ලෙස) පවතී අලුත් ස්වර සප්තකයක් ලෙස (එහෙත් මේ සියලු ස්වර C5, D5, E5 ආදී ලෙස පහේ ඉලක්කම සහිතව දැක්වේ). එහෙත් මෙම අලුත් ස්වර සප්තකය මීට පෙර තිබූ ස්වරවල සංඛ්‍යාතයන්ගේ දෙගුණය වේ. ඒ කියන්නේ පෙර හමුවූ A ස්වරයේ සංඛ්‍යාතය 440Hz වන අතර, ඉන්පසු හමුවන ස්වර සප්තකයේ A ස්වරය 880Hz වේ. ස (C) ස්වරයෙන් පටන් ගෙන ඊළඟට හමුවන ස ස්වරය දක්වා ඇති ස්වර 8 ස්වර අෂ්ඨකය (octave) ලෙස හැඳින්වෙනවා. මෙලෙසම C5 සවර සප්තකයේ අවසානයේ නැවත හමු වෙනවා C ස්වරයක්. එය C6 වේ. ඒ කියන්නේ C6 හි සංඛ්‍යාතය C5 හි සංඛ්‍යාතය මෙන් දෙගුණයකි. මේ ආදී ලෙස 1, 2, 3, 4, 5, 6 ආදී ලෙස ස්වර සප්තක කිහිපයක්ම පවතී. මේ සෑම සප්තයකයක්ම මීට පෙර සප්තකයේ ස්වරවල සංඛ්‍යාතය මෙන් දෙගුණයකි. මේ අනුව පැහැදිලිව පේනවා ඔක්ටේව් එක යම් සංඛ්‍යාතයක දෙගුණය හඟවන බව. ඔක්ටේව් යන්නට "දෙගුණය" යන තේරුම ලැබී ඇත්තේ ස්වර 8කට පසුව සංඛ්‍යාතය දෙගුණ වීම නිසාය.
දැන් අපි නැවත බලමු ෆිල්ටර් එකක බෑවුම ගැන. ඉහත රූපයේ දැක්වෙනවා බෑවුම -20dB/decade බව. ඒ කියන්නේ යම් සංඛ්‍යාතයක් ගෙන, එම සංඛ්‍යාතයේ සිට එහි දසගුණය හඟවන සංඛ්‍යාතය දක්වා පරාසය හෙවත් සංඛ්‍යාත ඩිකේඩ් එකක් තුළ ඩෙසිබල් 20කින් සංඥාව (සංඥාවේ වෝල්ටියතාව) දුර්වල/හායනය කරන බව (අටෙනුවේෂන්). එනම්, සෑම ඩිකේඩ් එකකදීම ඩෙසිබල් 20ක වෝල්ටියතා හායනයක් සිදු වේ. එහි ඍණ ලකුණ නොතිබුණා නම්, ඉන් කියන්නේ සංඛ්‍යාත ඩිකේඩ් එකක් තුළ ඩෙසිබල් 20කින් සංඥාවේ වෝල්ටියතාව වර්ධනය වන බව (ඇම්ප්ලිෆිකේෂන්). ඇත්තටම මෙම හායන ප්‍රමාණය ඕනෑම RC filter එකක පවතී. එය හයිපාස්ද ලෝපාස්ද යන්න වැදගත් නැහැ. 20dB/decade වෝල්ටියතා හායනය එක් කැප් එකක් හා එක් රෙසිස්ටරයක් සහිත ඕනැම RC filter එකකට ආවේණික වේ. හොඳින් මතක තබා ගන්න මෙහිදී සලකා බැලුවේ ජවය නොව වෝල්ටියතාවයි.
ඉහත ෆිල්ටරයේ බෑවුම දැක්වූයේ ඩිකේඩ් එකක් අනුසාරයෙනි. එයම ඔක්ටේව් යොදාගෙනද දැක්විය හැකියි. ඒ අනුව ඉහත ෆිල්ටරයේ බෑවුම -6dB/octave වේ. ඒ කියන්නේ යම් සංඛ්‍යාතයක් ගත් විට, එම සංඛ්‍යාතයත් එහි දෙගුණය හඟවන සංඛ්‍යාතයත් අතර සංඛ්‍යාත පරාසය තුළ සංඥාව (සංඥාවේ වෝල්ටියතාව) ඩෙසිබල් 6කින් හායනය වේ. සාමාන්‍යයෙන් ෆිල්ටර්වලදී අප ජවය වෙනුවට භාවිතා කරන්නේ වෝල්ටියතාවයි.
ඔබ දැනටමත් දන්නවා ඩෙසිබල් තුනක් යනු ජවයේ දෙගුණයක් බව (එහෙත් මෙහි ඍණ ඩෙසිබල් 3 බැවින්, එය ½ හෙවත් පවතින සංඥාවෙ ජවයෙන් අඩක් වේ). ඒ කියන්නේ සංඛ්‍යාතය දෙගුණ වන සෑම අවස්ථාවකදීම සංඥා ජවයේ ප්‍රබලතාව අඩක් බවට පත් වේ. ජවයට එසේ වුවද, වෝල්ටියතාව සලකන විට, ඩෙසිබල් 3 වෙනුවට 6 ලෙස සැලකීමට සිදු වෙනවා. (ඊට හේතුව ඔබ දැන් දන්නවා; ඩෙසිබල් ගණනය කරන සූත්‍රයේ 10 වෙනුවට 20 තිබුණා මතකද? ඒ කියන්නේ ජවය සම්බන්ධයෙන් කියන අගයන්ගේ දෙගුණය ගත යුතුයි වෝල්ටියතා ගැන කතා කරනකොට.) ඒ අනුව, ඍණ ඩෙසිබල් 6ක් යනු වෝල්ටියතාව අඩකින් අඩු වෙනවා.
ඔබට ඉතාම පහසුවෙන්ම dB/decade හා dB/octave වලින් එකක් දී ඇති විට අනෙක ගණනය කළ හැකියි. ඒ සඳහා පහත සම්බන්ධතාව මතක තබා ගන්න.
1dB/decade = 3.2dB/octave
ඒ අනුව, 6dB/octave අනෙක් ඒකකයට හරවන්න.
6dB/octave → (3.2 x 6) dB/decade = 20dB/decade (දළ වශයෙන්)
ඒ ඒ පරිපථයේ ස්වභාවය අනුව හෝ විශ්ලේෂණය කිරීමේ පහසුව/සම්ප්‍රදාය අනුව සමහර අවස්ථාවල අප වෝල්ටියතාවද තවත් අවස්ථාවල ජවයද භාවිතා කරනවා ඩෙසිබල් සමග. බැලූ බැල්මට මේ දෙක එකට යොදා ගැනීම පැටලිලි සහගත විය හැකියි. එහෙත් ඉහත රූපයේදී මෙන්ම බොහෝ පොතපතේ හා විස්තර කිරීම් තුළ මේ දෙවර්ගයම එකට භාවිතා කෙරෙනවා. බලන්න නැවත ඉහත රූපය. එහි හායනය පෙන්වන බෑවුම දක්වා ඇත්තේ වෝල්ටියතාව පදනම් කරගෙනයි (-20dB/decade හෝ -6dB/octave). එහෙත් එම රූපයේම Y අක්ෂයේ දක්වා ඇති ඩෙසිබල් අගයන් දක්වා ඇත්තේ ජවය පදනම් කරගෙනයි. ඔබ මේ දෙක වෙන වෙනම හඳුනාගැනීමට සමත් විය යුතුයි. සාමාන්‍යයෙන් කට්-ඕෆ් සංඛ්‍යාතයේදී -3dB හායනයක් සිදු වේය යන්න කොතරම් ගැඹුරට "ඉලෙක්ට්‍රොනික්ස් කාරයන්ගේ" සිත්වල පැලපැදියම් වෙලා තියෙනවාද කියතොත්, වෝල්ටියතා සමග කටයුතු කරන අවස්ථාවල -6dB ලෙස ලිවීම වඩා හිතකර හා නිරවුල් වුවත්, පුරුද්දට මෙන් -3dB ලෙස ලියනවා. එවැනි අවස්ථා තේරුම් ගැනීමට මෙතැන් සිට ඔබට හැකියි.
ඉලෙක්ට්‍රෝනික්ස් (electronics) ...