ප්රතිරෝධක මෙන් නොව, කැපෑසිටර් මාදිලි විශාල ගණනක් තිබේ. පරිපථ නිර්මාණයේදී යෙදිය යුත්තේ කුමන ධාරිත්රක මාදිලියක්ද යන්න ඔබට අවශ්ය ගතිගුණ අනුව දැන් තීරණය කළ හැකියි. ධාරිත්රක විවිධ කාර්යන් සඳහා උපයෝගි කර ගනී. ඒ එක් එක් කාර්ය සඳහා එක් ධාරිත්රක වර්ගයක්/මාදිලියක් පමණක් නොව, මාදිලි කිහිපයක් වුවද සුදුසු විය හැකියි. පහත රූපයේ මේ ගැන සාරාංශයක් දැක්වේ. සෙරමික්, ෆිල්ම්, හා ඉලෙක්ට්රොලයිටික් යන ප්රධාන කැප් වර්ග තුන යොදාගත හැකි අවස්ථා මෙහි දැක්වේ.

කැපෑසිටර් විභව බෙදුම් පරිපථ
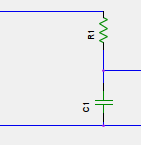
එය බැලූබැල්මට විභව පරිපථය සිහි කරවයි. ඇත්තටම මෙයත් එක්තරා විදියක විභව බෙදුම් පරිපථයක්. සාමාන්ය විභව බෙදුමේ තිබෙන ප්රතිරෝධක දෙක (හෝ කිහිපය) වෙනුවට ධාරිත්රක දෙකක් යොදා ගෙන ඇත. ඔබ මෙතෙක් උගත් සිද්ධාන්ත ඔස්සේ මෙම පරිපථය විග්රහ කරන්න. එකවරම ඔබට කිව හැකියි මෙම විභව බෙදුම සම්බන්ධ කර තිබෙන්නේ ස්ථාවර ඩීසී විදුලියකට නම්, ධාරිත්රක හරහා කිසිදු විදුලියක් ගමන් නොකර එම ඉන්පුට් විභවයෙන් කිසිදු අවුට්පුට් විදුලියක් o ස්ථායෙන් පිට නොකරන බව.
ඒ කියන්නේ මෙම විභව බෙදුම ක්රියාත්මක වන්නේ විචලනය වන විදුලි සැපයුමකට පමණි. අපි දැන් සිතමු සැපයුම් විදුලිය පරිපූර්ණ සයිනාකාර තරංග හැඩයක් සහිතයි කියා. එවිට ඔබට පුලුවන් මේ එක් එක් ධාරිත්රකය විසින් එම විදුලියට දක්වන ප්රතිභාදක අගයන් ගණනය කරන්නට. ඉහත රූපයේ කැප් දෙකෙහි අගයන් C1= 1u හා C2=1u ලෙස යොදා ගනිමින්, විදුලියේ සංඛ්යාතය හර්ට් 1000 නම්, සම්භාදක අගයන් ගණනය කරමු. එවිට C1 ධාරිත්රකය සඳහා, X = 1/( 2πfC) අනුව, ප්රතිභාදකය = 1/(2 x 3.1416 x 0.000001 x 1000) = 160 ohm වේ. එලෙසම C2 ධාරිත්රකයේ අගයත් එයම නිසා එහිත් X = 160 ohm වේ.
විදුලි සංඛ්යාතය වැඩි වූවොත් විභවය බෙදෙන ඉහත අනුපාතය වෙනස් වේවිද? නැත. සංඛ්යාතය කුමක් වුවත් එම අනුපාතය වෙනස් නොවේ. උදාහරණයක් මඟින්ම එය බලමු. ඉහත උදාහරණයේම හර්ට්ස් 1000 වෙනුවට 10000 වූවා යැයි සිතා ඉහත ගණනය කිරීම් නැවත කර බලන්න. එවිටද X1 = X2 = 16 ohm වේ. අනුපාතය 16:16 හෙවත් 1:1 වේ.
අනුපාතය එකමයි නේද? එහෙත් සංඛ්යාතය වෙනස් වන විට, ප්රතිබාධක අගයන් වෙනස් වේ (අනුපාතය වෙනස් නොවී). ප්රතිබාධකය වෙනස් වීම එම විභව බෙදුම හරහා යන ධාරාව අඩු/වැඩි කිරීමට බලපායි. සංඛ්යාතය වැඩිවන විට ප්රතිබාධකය අඩු වන නිසා, ඒ කියන්නේ සංඛ්යාතය වැඩිවන විට, විභව බෙදුමේ ගලා යන ධාරාව වැඩි විය යුතුයි. තවද, ඔබ පෙර උගත් පරිදිම මෙම ධාරාව වෝල්ටියතාවට වඩා අංශක 90කින් ඉදිරියෙන් ගමන් කරනවා.
තවද, ධාරිත්රක දෙකක් යොදා ඇති එම පරිපථයේ ගලා යන ධාරාව ගණනය කරන්නේ කෙසේද? එය සිදු කරන්නේ ප්රතිරෝධක දෙකක් යොදා ඇති විභව පරිපථයක ධාරාව ගණනය කරන විදියටමයි. මෙහිදී ඉහත ආකාරයට ධාරිත්රකවල ප්රතිබාධක ගණනය කර, ප්රතිබාධක (ප්රතිරෝධක) දෙක ශ්රේණිගතව තිබෙන බැවින් නිකංම එම අගයන් දෙක එකතු කර, වෝල්ටියතාව ඉන් බෙදීමයි කළ යුත්තේ.
ඒ කියන්නේ ධාරිත්රක දෙකක් ශ්රේණිගතව සම්බන්ධ කළ විට, ධාරිතාව 1/C1 + 1/C2 යන සූත්රය අනුව එකතු වුවත්; එම ධාරිත්රක දෙකෙන් ඇතිවන ප්රතිබාධක දෙකද පවතින්නේ ශ්රේණිගතව නිසා, ප්රතිබාධක යනුද ප්රතිරෝධ ලෙස සැලකෙන බැවින්, එම ප්රතිබාධක දෙක එකතු වන්නේ X1 + X2 යන සූත්රයට අනුවයි. (මෙලෙසම සමාන්තරගත ධාරිත්රක දෙකක ප්රතිබාධක ගණනය කිරීම සිදු කරන්නේ සමාන්තරගතව සම්බන්ධ කර තිබෙන සාමාන්ය ප්රතිරෝධක දෙකක සමක අගය සොයන ආකාරයටමයි.) ඒ කියන්නේ, ශ්රේණිගතව ඇති ප්රතිභාදක දෙකක සමක අගය
X = X1 + X2
සූත්රය අනුවද, සමාන්තරගතව ඇති ප්රතිභාදක දෙකක සමක අගය
1/X = 1/X1 + 1/X2
යන සූත්රයෙන්ද ගණනය කළ හැකියි. (ප්රතිභාදකය යනුද ප්රතිරෝධ වැනි නිසා, ප්රතිරෝධක සඳහා සමක අගයන් සොයන සූත්රම මේ සඳහාත් යොදා ගැනීම පුදුම විය යුතු දෙයක් නොවේ.)
දැන් පරිපූර්ණ සයිනාකාර විදුලියක් වෙනුවට වෙනත් ඕනෑම හැඩයකින් යුතු විදුලියක් ගමන් කළ විට සිදුවන දේත් ඔබට විග්රහ කරගැනීමට හැකියාවක් තිබිය යුතුයි. එහිදීත් විභවය බෙදෙන අනුපාතය වෙනස් නොවේ. එහෙත් ධාරාවේ ප්රමාණය වෙනස් විය හැකි සේම ධාරාවේ හැඩය විකෘති වන බවත් දැන් ඔබ දන්නවා.
විචලනය වන විදුලියක් ගමන් කරන විට, එම විදුලියේ සංඛ්යාතය අනුව ධාරිත්රකය යම් ප්රතිභාධක අගයක් හිමි කර ගන්නවා. එහෙත් ප්රතිරෝධකය එසේ නොවේ; එය සංඛ්යාතය කුමක් වුවත් එකම ප්රතිරෝධී අගයක් පමණක් පෙන්වනවා. පෙර සේම සිතමු C1=1u, R1=1.6k හා විදුලි සංඛ්යාතය හර්ට්ස් 1000 කියා. එවිට, ප්රතිබාධක අගය ඕම් 160 වන අතර ප්රතිරෝධි අගය එලෙසම කිලෝඕම් 1.6 අගයේ පවතී. එවිට, මෙහි විභවය බෙදෙන අනුපාතය 160:1600 හෙවත් 1:10 වේ. දැන් විදුලි සංඛ්යාතය 10000 කළේ නම්, එවිට ධාරිත්රකයේ ප්රතිබාධක අගය ඕම් 16 වන අතර, ප්රතිරෝධකයේ අගය නොවෙනස්ව පවතී. මේ අනුව දැන් විභවය බෙදෙන්නේ 16:1600 හෙවත් 1:100 අනුපාතයටයි. ඒ කියන්නේ විදුලි සංඛ්යාතය වෙනස් වන විට, විභවය බෙදෙන අනුපාතයත් වෙනස් වේ. දෙකම ධාරිත්රක වන ඉහත අවස්ථාවට වඩා මෙය වෙනස් නේද? පෙර අවස්ථාවේදී අනුපාතය වෙනස් නොවූයේ සංඛ්යාතය වෙනස් වන විට, ධාරිත්රක දෙකහිම ප්රතිබාධක අගයන් අනුරූපව වෙනස් වන නිසාය. පෙර ඔබ ඉගෙන ගත්තා ධාරිත්රකයක එක් රාජකාරියක් තමයි සංඛ්යාතය මත යැපෙන විචල්ය ප්රතිරෝධකයක් ලෙස ක්රියා කිරීම බව. පේනවා නේද මෙම රාජකාරිය තමයි මේ පරිපථයෙන් අපට ඉස්මතු වූයේ.
ඉහත පරිපථයේ ධාරිත්රකය යොදා තිබෙන්නේ ප්රතිරෝධයට උඩින්ය. එවිට සංඛ්යාතය වැඩිවන විට, ප්රතිබාධකය අඩුවන බැවින් යට ප්රතිරෝධකය දෙපස ඩ්රොප්වන වෝල්ටියතාව ඉහල යයි. ඒ කියන්නේ විභව බෙදුමෙන් පිටතට ලබා දෙන වෝල්ටියතාව වැඩි වේ. දැන් ඔබ පහත රූපයේ ආකාරයට ප්රතිරෝධකය හා ධාරිත්රකය උඩ යට මාරු කළ විට සිදුවන්නේ අනෙක් පැත්තයි. එනම්, විදුලියේ සංඛ්යාතය වැඩි වන විට, ධාරිත්රකයේ දෙපස ඩ්රොප්වන විභවය අඩු වීමයි. ඒ කියන්නේ පිටතට ලබා දෙන වෝල්ටියතාව අඩුවේ.
සම්භාදකය (Impedance)
ඔබ මෙතෙක් ඉගෙන ගත්තා ඕම්වලින් මනින ප්රතිරෝධයත්, ඕම්වලින්ම මනින ප්රතිබාධකයත් ගැන. මෙවැනිම ඕම්වලින් මනින තවත් රාශියක් තමයි සම්භාදකය කියන්නේ. එය Z අකුරින් සංඛේතවත් කෙරෙනවා. ඉතිං කුමක්ද මේ සම්භාදකය? සම්භාදකය සෑදෙන්නේ ප්රතිරෝධය හා ප්රතිබාධකය යන දෙකෙහි සංකලනයෙනි. මෙම ඉම්පීඩන්ස් යන වචනය/සංකල්පය ඉලෙක්ට්රොනික්ස්වල නිතරම භාවිතා කෙරෙන්නක් නිසා, මේ ගැන ඉතා හොඳ අවබෝධයක් ලබා ගත යුතුය. එය සූත්රයක් ලෙස පහත ආකාරයට පහසුවෙන්ම දැක්විය හැකියි.Z2 = R2 + X2
ගණිතය පිළිබඳ දැනුමක් ඇති අයට ඉහත සූත්රය දුටු විට, පයිතගරස් ප්රමේයය මතක් වෙනවා නේද? පහත දැක්වෙන්නේ එම පයිතගරස් ප්රමේයයි.
ඇත්තටම ඉහත සම්භාදකය ගණනය කරන සූත්රය පයිතගරස් (ඍජුකෝණී) ත්රිකෝණයකට ආදේශ කළ හැකියි. පාද තුනෙන් එම රාශි තුන නිරූපණය කෙරේ. එහිදී කර්ණයේ දිගින් Z (impedance) ලැබේ. රාශි තුනේ විශාලත්වයට අනුරූපව පාද තුනේ දිග තබන්න.
කෙසේ වෙතත්, සත්යම අර්ථයෙන් සම්භාදකය යන්න ප්රතිරෝධය හා ප්රතිභාධකයට වඩා වෙනස්ය. ඔබ දන්නවා ප්රතිරෝධකයක තාප උත්සර්ජනයක් සිදු වුවත්, ප්රතිභාධකයක තාප උත්සර්ජනයක් සිදු නොවන වග. ඒ දෙක වෙන් කොට හදුනා ගැනීමට ඇති හොඳම ක්රමය තාප උත්සර්ජනය සිදුවෙනවාද නැද්ද යන වගයි. තවද ප්රතිභාධකයක් පෙන්නුම් කරන අවස්ථාවක වෝල්ටියතාව හා ධාරාව අතර කලා වෙනසක් පවතින බව, හා ප්රතිරෝධකයක් පවතින අවස්ථාවක වෝල්ටියතාව හා ධාරාව සමකලාවේ පවතින බව තවත් වෙනස්කමක් මේ දෙකෙහි. එහෙත් සම්භාදකය යනු මේ දෙකෙහිම සංකලනයක් බැවින්, සම්භාදකයකත් යම් තාප උත්සර්ජනයක් සිදු වෙනවා. එලෙසම සම්භාදකයක් පවතින අවස්ථාවකත් වෝල්ටියතාව හා ධාරාව අතර කලා වෙනසකුත් පවතිනවා. මෙම තාප උත්සර්ජනයේ ප්රමාණය හා ඇතිවන කලා වෙනසේ ප්රමාණය තීරණය වන්නේ සම්භාදකය සෑදීමට හවුල් වන ප්රතිරෝධයේ හා ප්රතිභාධකයේ අගයන් මතයි. ඉහත සම්භාදක ත්රිකෝණය නැවත බලන්න. එහි ප්රතිරෝධය හඟවන පාදය විශාල වන විට, සම්භාදකය ප්රතිරෝධයේ ගුණයට වඩ වඩා ළං වෙනවා. ඒ කියන්නේ සම්භාදකයේ ප්රතිරෝධි ගුණ වැඩි වෙනවා. එවිට, තාප උත්සර්ජනය වැඩි වෙනවා; කලා වෙනස අඩු වෙනවා. එලෙසම, එම ත්රිකෝණයේ ප්රතිභාධකය හඟවන පාදය විශාල වන විට, සම්භාදකයේ ප්රතිභාදක ගුණ වැඩි වෙනවා. එවිට, තාප උත්සර්ජනය ක්රමයෙන් අඩු වෙනවා; කලා වෙනස ක්රමයෙන් වැඩි වෙනවා. මේ ලෙස, එක පාදයක් ශූන්ය වන විට, ඉතිරි අනෙක් පාදය කර්ණය මතට සමපාත වෙනවා. එය තමයි මුලින් පැවසුවේ සම්භාදකයක් සමහරවිට ප්රතිරෝධයක් හෝ ප්රතිභාදකයක් බවට වුවත් පත් විය හැකියි කියා. එවිට, සම්භාදකයේ පවතින්නේ එම ප්රතිරෝධයේ හෝ ප්රතිභාදකයේ ගුණය පමණි.
තවදුරටත් ධාරිත්රකයක් හා ප්රතිරෝධකයක් එකිනෙකට සම්බන්ධ කිරීමේදී අැති වන සම්භාදකය ගැන සොයා බලමු. ඕනෑම උපාංග දෙකක් එකිනෙකට සම්බන්ධ කළ හැකි ආකාර පවතින්නේ දෙකක් පමණක් බව ඔබ දන්නවා. ඒ අනුව කැප් එකක් හා රෙසිස්ටරයක් එකිනෙකට ශ්රේණිගතව හෝ සමාන්තරගතව සම්බන්ධ කළ හැකියි. පළමුව සමාන්තරගත අවස්ථාව බලමු. මෙය parallel RC circuit නම් වේ.
සාමාන්ය විදුලිය සම්බන්ධ රීති අනුව එම උපාංග දෙක දෙපස ඩ්රොප්වන්නේ එකම වෝල්ටියතාවකි. එමනිසා වෝල්ටියතාවේ අමුතුවෙන් ගණනය කරන්නට දෙයක් නැත. එහෙත් මෙහි ධාරාව තරමක් සංකීර්ණ ස්වභාවයක් ගන්නවා. ඊට හේතුව ඔබට සිතා ගත හැකි විය යුතුයි. පළමුවෙන්ම කිව යුත්තේ ලබා දෙන්නේ ඒකාකාර ස්ථාවර ඩීසී විදුලියක් නම්, ධාරිත්රකය එතැන තිබුණත් නැහැ වගේ. එවිට, ඉතාම සරලව භාහිරව යෙදූ සැපයුම් විභවය ප්රතිරෝධකයේ ඕම් අගයෙන් බෙදා ඒ හරහා යන ධාරාව පහසුවෙන්ම ගණනය කළ හැකියි. ධාරිත්රකය හරහා කිසිදු ධාරාවක් නොගලයි. තවද, වෝල්ටියතාව හා ධාරාව සමකලාවේ පවතී (ධාරිත්රකයේ බලපෑම ශූන්ය නිසා).
එහෙත් මෙහි තිබෙන්නේ විචලනය වන විදුලියක් නම් තමයි සංකීර්ණ තත්වය ඇති වන්නේ. එවිට උපාංග දෙක හරහාම ධාරා දෙකක් ගලා යයි. ප්රතිරෝධකය හරහා යන ධාරාව වෝල්ටියතාව සමග සමකලාවේ පවතින අතර, ධාරිත්රකය හරහා යන ධාරාව වෝල්ටියතාවට වඩා අංශක 90ක් ඉදිරියෙන් විෂම කලාවෙන් ගමන් කරනවා. ඉතිං ගමන් කරන මුලු ධාරාව කොපමණද? මුලු ධාරාව කෙසේ වෙතත් ප්රතිරෝධකය හා ධාරිත්රකය හරහා වෙන වෙනම යන ධාරා දෙක පහසුවෙන්ම ගණනය කළ හැකියි. භාහිර වෝල්ටියතාව ප්රතිරෝධකයේ අගයෙන් බෙදීමෙන් ප්රතිරෝධකයේ ධාරාවද (I = V/R) , එම වෝල්ටියතාව ධාරිත්රකයේ ප්රතිභාදකයේ අගයෙන් බෙදීමෙන් ධාරිත්රකය හරහා යන ධාරාවද (I=jV/X) ගණනය කළ හැකියි (j අකුර ගැන විස්තර මොහොතකින් දැක්වේ; කෙටියෙන් කියතොත් V/X මඟින් ලැබෙන ධාරාව අංශක 90ක කලා වෙනසකින් පවතින බව මින් හැඟවේ; j සහිත සංඛ්යා ගණිතයේදී “සංකීර්ණ සංඛ්යා” නමින් හැඳින්වේ). j අකුර නොමැතිවත් Ic = V/X ලෙස ඉහත සූත්රය ලිවිය හැකියි. මෙවිට ධාරාවේ නියම අගය ලැබුණත් එහි කලා වෙනස ගැන කිසිදු අදහසක් ඉන් නොදේ. j අකුර තිබෙන විට, ධාරාවේ අගයත්, අංශක 90 කලාවත් එකවර නිරූපණය කරයි.
සටහන
ඉහත පැහැදිලි කළ ලෙස j අකුර ඇතිවත් නැතිවත් මෙම රාශින් දැක්විය හැකිය. එහෙත් ගණිතානුකූලව නම් මෙම නිරූපණ දෙකෙහි විශාල වෙනසක් ඇත. j ඇති විටක, සංකීර්ණ සංඛ්යා රීතින් අනුගමනය කළ යුතුය. j යොදාගන්නා විට, ඉහත parallel RC පරිපථයෙන් ගලා යන මුලු ධාරාව
 ලෙස
ලිවිය හැකිය. එවිට
මෙම සුලු කිරීම සිදු කරන්නේ
සංකීර්ණ සංඛ්යා රීතින් අනුව
නිසා,
ලෙස
ලිවිය හැකිය. එවිට
මෙම සුලු කිරීම සිදු කරන්නේ
සංකීර්ණ සංඛ්යා රීතින් අනුව
නිසා,  ලෙස
එය සිදු කළ යුතුය.
ලෙස
එය සිදු කළ යුතුය.එහෙත්, j අකුර නොයොදන විට, එතැන සංකීර්ණ සංඛ්යා රීතින් වලංගු නොවන බැවින්, මුලු ධාරාව
 ලෙස
කිසිසේත් ලිවිය නොහැකිය.
එවිට,
V/R හා V/X
යන පද දෙක
දෛශික ආකලනය හෙවත් පයිතගරස්
ප්රමේය යොදා සුලු කළ යුතු
බව අමුතුවෙන් කිව යුතු වෙනවා.
ඔබට පෙනෙනවා
ඇති j අකුර
තිබුණත් ප්රායෝගිකව එම සුලු
කිරීම සිදු කරන්නේ පයිතගරස්
ප්රමේය අනුවයි. මෙතැන
තිබෙන්නේ ගණනය කරන ක්රමයේ
වෙනසක් නොව; ඉදිරිපත්
කරන ක්රමයේ වෙනසකි. j
දුටු ගමන්
සංකීර්ණ සංඛ්යා ගැන දන්න අය
දන්නවා කුමක් කළ යුතුද කෙසේ
සුලු කළ යුතුද වග. එය
නැති විටක, මෙසේ
සුලු කළ යුතු යැයි අමුතුවෙන්
පැවසීමට සිදු වෙනවා.
ලෙස
කිසිසේත් ලිවිය නොහැකිය.
එවිට,
V/R හා V/X
යන පද දෙක
දෛශික ආකලනය හෙවත් පයිතගරස්
ප්රමේය යොදා සුලු කළ යුතු
බව අමුතුවෙන් කිව යුතු වෙනවා.
ඔබට පෙනෙනවා
ඇති j අකුර
තිබුණත් ප්රායෝගිකව එම සුලු
කිරීම සිදු කරන්නේ පයිතගරස්
ප්රමේය අනුවයි. මෙතැන
තිබෙන්නේ ගණනය කරන ක්රමයේ
වෙනසක් නොව; ඉදිරිපත්
කරන ක්රමයේ වෙනසකි. j
දුටු ගමන්
සංකීර්ණ සංඛ්යා ගැන දන්න අය
දන්නවා කුමක් කළ යුතුද කෙසේ
සුලු කළ යුතුද වග. එය
නැති විටක, මෙසේ
සුලු කළ යුතු යැයි අමුතුවෙන්
පැවසීමට සිදු වෙනවා.එවිට ඔබට එකවරම සිතේවී මෙම වෙන වෙනම ගමන් කරන ධාරා දෙකේ එකතුව නේද මුලු ධාරාව විය යුත්තේ කියා. ඉහත සටහන අනුව පිළිතුර ඔව් හෝ නැත යනුවෙන් දිය හැකියි (j තිබීම හෝ නොතිබීම මත). මේ ගැන විමසමු. එය එතරම් සරල නොවන්නේ මෙතැන ප්රතිරෝධකය හරහා යන ධාරාව හා ධාරිත්රකය හරහා යන ධාරාව අතර කලා වෙනසක් තිබීමයි. ප්රතිරෝධකය හරහා යන ධාරාව හා ධාරිත්රකය හරහා යන ධාරාව අතර කලා වෙනසක් තිබෙන්නේ ඇයි? එය මෙලෙස තර්ක කර බලන්න. ප්රතිරෝධකයේ වෝල්ටියතාව හා ප්රතිරෝධකයේ ධාරාව අතර කලා වෙනසක් නැත. එම වෝල්ටියතාවමයි සමානතරගතව සම්බන්ධ කර තිබෙන නිසා ධාරිත්රකය දෙපසත් තිබෙන්නේ. ඒ කියන්නේ ප්රතිරෝධක වෝල්ටියතාව හා ධාරිත්රක වෝල්ටියතාව අතරත් කලා වෙනසක් සිදු නොවේ. එහෙත් ධාරිත්රකයේ වෝල්ටියතාවට වඩා අංශක 90ක් ඉදිරියන් ධාරිත්රකයේ ධාරාව ගලා යනවා. ඒ කියන්නේ ධාරිත්රකයේ වෝල්ටියතාව හා ධාරිත්රකයේ ධාරාව අතර අංශක 90ක කලා වෙනසක් පවතිනවා. ඉතිං එම කලා වෙනසම තමයි ධාරිත්රක ධාරාව විසින් ප්රතිරෝධකයේ ධාරාවට ඇති කරන්නේ.
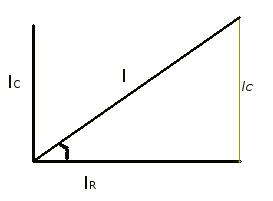
ඉහත විස්තරය රූපමය ආකාරයට පහත දැක්වේ. මෙලෙස එකම උපාංගයක හෝ වෙනස් උපාංගවල ධාරා/වෝල්ටියතා අතර කලා වෙනස පෙන්වීමට ගන්නා රූප phasor diagram ලෙස හැඳින්වෙනවා. මෙහිදී සරල රේඛා ඛණ්ඩ මඟින් තමයි ධාරාවන් හා වෝල්ටියතාවන් දක්වන්නේ. රේඛාවේ දිගින් වෝල්ටියතාවේ හා ධාරාවේ විශාලත්වය අවශ්ය නම් පෙන්විය හැකියි. කලා වෙනස එම රේඛා අතර පවතින කෝණය මඟින් හඟවනවා. තිරස් රේඛාව reference line ලෙස සැලකෙනවා. වැඩිපුර රාශින් එකමත සමපාත වන විට ඒවා දක්වන්නේ මෙම රෙෆරන්ස් ලයින් එකේය. ධණ කෝණ රෙෆරන්ස් ලයින් එකේ සිට වාමාවර්ථවයි සටහන් කරන්නේ. විශාල තොරතුරු ප්රමාණයක් එකවරම සරලව දක්වන නිසා, ෆේසර් ඩයග්රැම් නැතිවම බැරිය.
බලන්න ඉහත රූපයේ මා පෙර විස්තර කළ සියල්ල රූපමය වශයෙන් පැහැදිලිව දැක්වෙනවා. කොලපාටින් දැක්වෙන රෙසිස්ටරයේ ධාරාව (IR) හා නිල්පාටින් දැක්වෙන රෙසිස්ටරයේ වෝල්ටියතාව (VR) අතර කලා වෙනසක් නැති නිසා එක මත එක එම රේඛා පවතිනවා (සමපාත වෙනවා). රතුපාටින් දැක්වෙන කැප් එකේ වෝල්ටියතාවද (VC) රෙසිස්ටරයේ වෝල්ටියතාවට සමානයිනෙ. එයත් VR, IR රේඛාව සමග සමපාත වෙනවා. දැන් කැප් එකේ ධාරාව (IC) අංශක 90කින් ඉදිරියෙන් (ධණ) ගමන් කරනවා; එය ඉහත රේඛාවට අංශක 90ක් පිහිටන සේ ඇඳිය හැකියි. ධණ කෝණයක් ෆේසර් ඩයග්රැම් එකක පෙන්වන්නේ ඉහත ආකාරයටයි. දැන් සියලු විස්තර එකවර ඉහත ෆේසර් ඩයග්රැම් එකෙන් පැහැදිලිවම පෙනෙනවා නේද? වඩා පැහැදිලි වීම පිණිස මා එක උඩ එක සමපාත වන රාශි විවිධ වර්ණවලින් දක්වා ඇතත්, ප්රායෝගිකව ඒ සියල්ල එකම රේඛාවක සටහන් කරනවා.
දැන් නැවත අප මුලින් කතා කරමින් සිටි මුලු ධාරාව ගණනය කිරීම සලකා බලමු. මෙම කලා වෙනස නිසා නිකංම ධාරා අගයන් දෙක එකතු කළ නොහැකියි. එම මුලු ධාරාව පහසුවෙන් ගණනය කළ හැකි ක්රමය මෙයයි. පළමුව ධාරිත්රක ප්රතිභාදක අගය හා ප්රතිරෝධකයේ ප්රතිරෝධක අගය යන දෙකෙහි සමක අගය සෙවිය යුතුය. මෙතැන තිබුණේ නිකංම ප්රතිරෝධක දෙකක් නම්, මෙය සමාන්තරගත සම්බන්ධයක් නිසා, 1/R = 1/R1 + 1/R2 යන සූත්රයෙන් සමක ප්රතිරෝධය සෙවිය හැකිව තිබුණා. එහෙත් මෙතැන තිබෙන්නේ ප්රතිරෝධකය දෙකක් නොවේ; ඒ වෙනුවට ප්රතිරෝධකයක් හා කැප් එකේ ප්රතිභාදකයයි. ඉහත කියූ කලා වෙනස නිසා, මෙම අවස්ථාවට භාවිතා කෙරෙන සූත්රය තරමක් වෙනස්ය. මෙහිදී ගණිතයේ හමුවන “සංකීර්ණ සංඛ්යා” (complex number) සංකල්පය භාවිතා කිරීම ඉතාම පහසුයි (සංකීර්ණ යන නම මෙම සංඛ්යා සඳහා යොදා ගත්තද ඉන් කිසිදු අමාරු/සංකීර්ණ කමක් හැඟවෙන්නේ නැත; එය හුදු නමක් පමණි; එනිසා නමට බිය නොවන්න; මෙම පාඩම් මාලාවේ ගණිත අතිරේකයක සංකීර්ණ සංඛ්යා ගැන සරල පැහැදිලි කිරීමක් සිදු කෙරේ). සංකීර්ණ සංඛ්යා නිරූපණය (notation) යොදාගෙන සමාන්තරගතව සම්බන්ධිත ප්රතිරෝධකයක හා ධාරිත්රකයක සමක ප්රතිරෝධය සොයන සූත්රය පහත දැක්වේ (j යනු සංකීර්ණ සංඛ්යාවල භාවිතා වෙන සංඛේතයකි; ගණිත අතිරේකය බලන්න වැඩි විස්තර සඳහා).
මෙය සාමාන්ය සමානතරගත සමක ප්රතිරෝධය සොයන සූත්රයට බොහෝ සමානයි නේද? එකම වෙනස ප්රතිබාධක පදයට ඉදිරියන් j තිබීමයි. j අකුරක් සහිත අවස්ථාවක නිකංම සාමාන්ය අංක ගණිතයේ හමුවන එකතු කිරීම කළ නොහැකියි. ඔබට පෛතගරස් ප්රමේය යෙදීමට සිදු වෙනවා. (එනම්, සරල අංග ගණිත එකතුව වෙනුවට දෛශික ආකලනය/එකතුව කළ යුතු වෙනවා.) ඔබට හැකියි ඉහත සූත්රයේ පද තුන පයිතගරස් ඍජුකෝණී ත්රිකෝණයකට ආදේශ කරන්නට.
සමහර පොත්වල ඉහත සූත්රයම පහත ආකාරවලටද ලියනවා. මෙහිදී සිදු කර ඇත්තේ උඩ තිබෙන j යටට (හරයට) යැවීමයි. එවිට ධණ සලකුණ ඍණ බවට පත් වෙනවා (එය සංකීර්ණ සංඛ්යාවල රීතියකි). උඩ සූත්රය වඩා පහසු බව මාගේ හැඟීමයි.
දැන් R හා X අගයන් සූත්රයට ආදේශ කරන්න (j අකුර නැතැයි සිතා). ඉන් 1/R හා 1/X පද දෙක සුලු කරන්න. එම අගයන් ඉහත ත්රිකෝණයට ආදේශ කරන්න. දැන් සුපුරුදු පෛතගරස් ප්රමේය අනුව සුලු කරන්න ((1/Z)2 = (1/X)2 + (1/R)2). එවිට එම ත්රිකෝණයේ කර්ණයෙන් ලැබෙන්නේ 1/Z පදයයි. ඔබට අවශ්ය 1/Z නොවේනෙ; ඔබට අවශ්ය Z පදයයි. ඉතිං ඉහත ලැබුණු Z අගයෙ පරස්පරය ගත් විට ලැබෙන්නේ Z අගයයි. (ඔබට අවශ්ය නම්, කෙලින්ම ඉහත සූත්රය වීජීය වශයෙන් සුලු කර ලැබෙන අවසන් (ටිකක් බය හිතෙන තරමට විශාල) සූත්රයට ප්රතිරෝධකයේ හා ප්රතිභාදකයේ අගයන් ආදේශ කරද Z අගය ගණනය කළ හැකියි.) දැන් ඔබට ප්රශ්නයක් වේවි එතකොට අර j අකුරට කුමක් සිදු වූවාද කියා. ඇත්තටම එම j අකුර නිසා තමයි අපට ත්රිකෝණයක් භාවිතා කිරීමට සිදු වූයේ (එය සංකීර්ණ සංඛ්යා ඉගෙනීමේදී වැටහේවි). j හි බලපෑම එයයි; අංකගණිත ආකලනය වෙනුවට දෛශික ආකලනය සිදු කරන ලෙසයි ඉන් කියන්නේ. ඉහත 1/Z ගණනය කළ ක්රියාපටිපාටිය සංකීර්ණ සංඛ්යාවලදී කෙටියෙන් සංකීර්ණ සංඛ්යාවේ magnitude (විශාලත්වය) සොයනවා යනුවෙන් හැඳින්වෙනවා. එය පහත ආකාරයට ලිවිය හැකියි. ගණිතයේදී යම් ගණිත ප්රකාශයක් මැදි කොට | | යන්න ඇති විට ඉන් කියන්නේ විශාලත්වය හෙවත් නිරපේක්ෂ අගය (absolute value) සොයන ලෙසයි.

ඔබට නිකමට හෝ හිතෙනව නම්, සංකීර්ණ සංඛ්යා නොයොදා මෙය ගණනය කිරීමට ඇත්නම් කියා, ඊටද යම් පිළියමක් ඇත. සංකීර්ණ සංඛ්යා හෝ j අකුර හෝ ගැන නොසිතන්න. කෙලින්ම පයිතගරස් ත්රිකෝණයට ඉහත පෙන්නුම් කළ ආකාරයට අගයන් ආදේශ කර ගණන සුලු කරන්න. ඇත්තෙන්ම j අකුර තිබීමෙන්ද අපට කියන්නේ එසේ කරන්න කියාය. එනම් X හා R අගයන් පහත සූත්රයට කෙලින්ම ආදේශ කර ගණන සුලු කරන්න.

ඉහත ආකාරයකට Z අගය ගණනය කළ පසු, වෝල්ටියතාව එම Z අගයෙන් බෙදූවිට ලැබෙන්නේ එම පරිපථ කොටසේ මුලු ධාරාවයි. එය I = V/Z යනුවෙන් ලියනවා. (මෙයත් ඕම් නියමය තමයි. R වෙනුවට Z ආදේශ කර ඇත.) තව එක් දෙයක් ඔබට ගණනය කිරීමට සිදු වෙනවා. එනම් මෙම මුලු ධාරාව වෝල්ටියතාව සමග ඇති කලා වෙනසයි. එය හැමවිටම අංශක 90ට අඩු කලා කෝණයකි. එය ගණනය කරන්නේ කෙසේද? මෙය රූපමය වශයෙන් දැක්වූ විට ඔබට පහසුවෙන්ම වැටහේවි. ඉහත දැකවූ ෆේසර් ඩයග්රැම් එකේම ඔබ මේ දැන් ගණනය කළ මුලු ධාරාව අඳින්න. මෙහි a කෝණය තමයි අපට දැන ගැනීමට අවශ්ය වන්නේ.
සංකීර්ණ සංඛ්යා රීතින්ම යොදාගෙන පහසුවෙන්ම ඔබට එම මුලු ධාරාව වෝල්ටියතාව සමග ඇති කරගන්නා කලා වෙනස ගණනය කිරීමට හැකියි. පෙර පෙන්වා දුන් පරිදි, මුලු ධාරාව
 යන
සූත්රයෙන් ලැබේ. එවිට
මෙම සංකීර්ණ සංඛ්යාවේ argument
එක සෙවූ විට
ලැබෙන්නේ කලා කෝණයේ අගයයි.
එනිසා,
යන
සූත්රයෙන් ලැබේ. එවිට
මෙම සංකීර්ණ සංඛ්යාවේ argument
එක සෙවූ විට
ලැබෙන්නේ කලා කෝණයේ අගයයි.
එනිසා,
සංකීර්ණ සංඛ්යා ගැන දැනුමක් නැතිනම්, කලා කෝණය = tan-1(IC/IR) යන ප්රතිලෝම ත්රිකෝණමිතික අනුපාතයෙන් වුවද එය පහසුවෙන්ම සෙවිය හැකියි. ඉහත ත්රිකෝණමිතික අනුපාතය ලැබුණේ ඉහත දැක්වෙන ෆේසර් ඩයග්රැම් එකෙන්ය. බලන්න එහි ධාරිත්රක ධාරාව ප්රතිරෝධක ධාරාවට ලබ්භකව පවතිනවා. ඉතිං a කෝණයට IC සම්මුඛ පාදයද IR බද්ධ පාදයද වෙනවා. එවිට, tan(a) = සම්මුඛ පාදය/ බද්ධ පාදය නිසා, tan(a) = IC/IR නිසා, a = tan-1 (IC/IR) වේ. එය වඩාත් පැහැදිලි වේවි පහත රූපයෙන්.
අපි දැන් ගැටලුවක් ආශ්රයෙන් මෙය තවදුරටත් ඉගෙන ගමු. පහත රූපය බලන්න.
ප්රතිරෝධකයේ අගය 1K ලෙස දී ඇත. එනිසා, එම ප්රතිරෝධකය හරහා ගලා යන ධාරාව, IR = 10/1000 = 0.01 A හෙවත් 10mA වේ.
ධාරිත්රකයේ ප්රතිභාදක අගය, X = 160 ohm වේ. ඒ අනුව ධාරිත්රකය හරහා ගලා යන ධාරාව, IC = j(10/160) = j0.0625A හෙවත් j62.5mA වේ. j අකුර තිබීමෙන් කියන්නේ මෙම ධාරාව වෝල්ටියතාවට වඩා අංශක 90කින් ඉදිරියෙන් සිටින බවයි.
දැන් සමක සම්භාදක අගය, 1/Z = 1/R + j(1/X) අනුව, 1/Z = 1/1000 + j(1/160) වේ. මෙය පෛතගරස් ප්රමේය (හෙවත් දෛශික ආකලනය) අනුව සුලු කළ යුතුය. එවිට,
(1/Z)2 = (1/1000)2 + (1/160)2 → (1/Z)2 = 0.000040062 → 1/Z = 0.006329494 වේ. එවිට,
Z = 1/0.006329494 = 158 ohm.
එමනිසා, පරිපථයේ ගලා යන මුලු ධාරාව V/Z = 10/158 = 0.0633A හෙවත් 63mA වේ.
දැන් මෙම ධාරාවේ කලාව සොයමු. කලා කෝණය = Arg(IR + jIC) = Arg(10 + j63) = 80O
ආර්ග්යුමන්ට් එකට ධාරාවේ අගයන් ආදේශ කරන විට, එම අගයන් දෙකම එකම මිම්මෙන් ඇතුලු කරන්න. ඒ කියන්නේ දෙකම ඇම්පියර් හෝ දෙකම මිලිඇම්පියර්වලින්. මෙම කෝණය ධණ බැවින්, ධාරාව විභවයට වඩා ඉදිරියෙන් ගමන් කරනවා. ඇත්තටම RC circuit වල හැමවිටම ලැබෙන මුලු ධාරාව විභවයට වඩා ඉදිරියෙන් ගමන් කරනවා. (පසුව ඉගෙන ගන්නා RL circuit වල මුලු ධාරාව හැමවිටම විභවයට පිටුපසින් ගමන් කරනවා.)
දැන් ප්රතිරෝධකයක් හා ධාරිත්රකයක් ශ්රේණිගතව සම්බන්ධ වන අවස්ථාව සලකමු. මෙය Series RC circuit ලෙස හැඳින්වෙනවා.
ඉලෙක්ට්රෝනික්ස් (electronics) ...









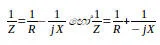


Comments
Post a Comment
Thanks for the comment made on blog.tekcroach.top