ප්රේරණතාව හා ඉන්ඩක්ටර්
පැසිව් ඉලෙක්ට්රොනික් උපාංග අතර තිබෙන තවත් වැදගත් උපාංගයක් තමයි ඉන්ඩක්ටර් එක (ප්රේරකය හෝ "කොයිල් එක"). ප්රේරණතාව (inductance) අපට අවශ්ය පරිදි ඇති කළ හැකි ලෙසට සකස් කළ ඇටවුමකට තමයි ප්රේරකය (inductor) කියා කියන්නේ. ඉන්ඩක්ටරයක පවතින ඉන්ඩක්ටන්ස් එක මනින ඒකකය Henry (H) වේ. සාමාන්යයෙන් (ෆැරඩ්වල මෙන්ම) හෙන්රි යනු විශාල ඒකකයකි. එමනිසා බහුලව හමුවන්නේ මිලිහෙන්රි හා මයික්රොහෙන්රි වේ.
මුලින්ම "ප්රේරණය" (induction) යන්නෙහි තේරුම දත යුතුය. එහි සාමාන්ය සිංහල තේරුම "යමක් තුල යම් ගතිගුණයක් ඇති කිරීම" යන්නයි. උදාහරණයක් ලෙස, ඔබේ දෙමව්පියන්ගේ හොඳ හැසිරීම නිසා ඔබ තුළත් නිරායාසයෙන්ම හොඳ ගතිගුණ ප්රේරණය වෙනවා.
ඉලෙක්ට්රොනික්ස්වලදීද තේරුම එයමයි. මෙහිදී ගතිගුණය ලෙස සලකන්නේ විදුලියයි. ඒ අනුව (විදුලි) ප්රේරණය යනු යම් සන්නායකයක නොතිබූ විදුලියක් පිටතින් ඒ තුළ ඇති කිරීමයි. එසේ ප්රේරණය වන විදුලිය ඒ ඒ අවස්ථාවල වෙනස් විය හැකියි. ඒ කියන්නේ එක් අවස්ථාවක A නම් සන්නායකයේ යම් වෝල්ටියතාවක් ප්රේරණය වූවා යැයි සිතන්න. එලෙසම තවත් B නම් සන්නායකයක් තුළද වෝල්ටියතාවක් ප්රේරණය කළා යැයි සිතමු. මෙම වෝල්ටියතා දෙකම සමාන හෝ අසමාන විය හැකියි. ඒ එක් එක් අවස්ථාවේදී කොපමණ වෝල්ටියතාවක් ප්රේරණය වනවාදැයි රඳා පවතින්නේ සාධක කිහිපයක් මතයි. කෙසේ හෝ වේවා, විවිධ වෝල්ටියතා අගයන් ප්රේරණය වීමේ හැකියාව තමයි ප්රේරණතාව යනුවෙන් හැඳින්වෙන්නේ. උදාහරණයක් ලෙස, ඉහත A සන්නායකයේ ප්රේරිත විදුලිය B ට වඩා වැඩි නම්, A හි ප්රේරණතාව වැඩියි යනුවෙන් සැලකිය හැකියි.
ප්රේරණය නම් ක්රියාවලිය පිටුපස සිටින්නේ විද්යුත් චුම්භක (electromagnet) ක්රියාකාරිත්වය වේ. එමනිසා කෙටියෙන් චුම්භක (magnet) හා විද්යුත් චුම්භක ගැන පළමුව දැනගමු. ඔබ දන්නවා චුම්භකයක ධ්රැව (pole) දෙකක් තිබෙනවා උතුර (North) හා දකුණ (South) ලෙස. සමාන ධ්රැව විකර්ෂණය කරන අතර, අසමාන ධ්රැව ආකර්ෂණය කරයි. චුම්භකයක් වටා චුම්භක ක්ෂේත්රයක් (magnetic field) ඇති කරනවා (හරියටම විදුලි ආරෝපණයක් විද්යුත් ක්ෂේත්රයක් ඇති කරනවා සේ). එම ක්ෂේත්රය තුළ තිබෙන වෙනත් චුම්භක හා සන්නායක්වලට ඉන් බලපෑමක් ඇති වෙනවා. එක් කාන්දමක් තවත් කාන්දමක ස්පර්ශ නොකර එහෙත් චලනයක් ඇති කළ හැක්කේ මෙම ක්ෂේත්රය නිසාය. මෙම චුම්භක ක්ෂේත්රය කාන්දමේ ධ්රැවය ආසන්නයේ ප්රබල වුවත්, ඉන් ඈත් වන විට ඉතා සීඝ්රයෙන් දුබල වෙනවා.
"කාන්දම් කෑලිවල" විතරක් නොවේ කාන්දම් හැකියාව පවතින්නේ. ඕනෑම සන්නායකයක් තුළින් විදුලි ධාරාවක් යන විටත් එම සන්නායකය අවට චුම්භක ක්ෂේත්රයක් හටගනී. එලෙස හට ගන්නා චුම්භක ක්ෂේත්රය පහත රූපයේ දැක්වෙන සේ "දකුණත් රීතිය" (Right-hand rule) මඟින් දත හැකියි. විදුලිය ගමන් කිරීම නිසා මෙලෙස ඇතිවන චුම්භකවලට තමයි විද්යුත් චුම්භක යන නම ව්යවහාර වෙන්නේ. විද්යුත් චුම්භකයක ඇතිවන චුම්භක ක්ෂේත්රය හා නිකංම කාන්දම් කෑලිවලින් ඇතිවන චුම්භක ක්ෂේත්රය අතර කිසිම වෙනසක් නැහැ. දෙකෙහිම ගතිගුණ එකමය.
සම්මත
ධාරාව ගලා යන දිශාවට මාපොට
ඇඟිල්ල පිහිටන සේ කම්බිය
අල්ලාගත් විට,
අනෙක්
ඇඟිලි කැරකී ඇති දිශාව ඔස්සේ
චුම්භක ක්ෂේත්ර වළලු/මුදු
(loop/ring)
පිහිටයි.
ධාරාව
වැඩිවන විට එම චුම්භක ක්ෂේත්රය
වැඩි වේ;
එනම්
විද්යුත් චුම්භකය ප්රබල
වේ.
එකම
දිශාවට ධාරාව ගමන් කරන සේ එක
ළඟින් පිහිටි මෙවැනි කම්බි/සන්නායක
ගණන වැඩි වන විටද චුම්භක
ක්ෂේත්ර එකට එකතු වීමෙන්
ප්රබල වේ.
කම්බියක්
තුළින් ධාරාවක් ගැලීමේදී
ඇතිවන චුම්භක ක්ෂේත්රය ගැන
නැවත බලමු.
සිතන්න
ඈම්ප් 2ක්
යනවා කියා.
එවිට,
යම්
චුම්භක ක්ෂේත්රයක් ඇති වෙනවා.
එය
ඈම්ප් 4ක්
දක්වා වැඩි කරමු.
එවිට,
මෙම
ක්ෂේත්රය තවත් ප්රබල වෙනවා;
චුම්භක
වලලු තවත් විශාල වෙනවා.
එනම්
ක්ෂේත්රය ප්රසාරණය වෙනවා.
එය
ඈම්ප් 1ක්
දක්වා අඩු කරමු.
එවිට
ක්ෂේත්රය හැකිලෙනවා.
මෙය
ක්ෂණිකව සිදු වෙනවා.
ඒ
කියන්නේ වයර් එක තුළින් ගලා
යන ධාරාව/විදුලිය
වෙනස් වන විට,
ඊට
අනුරූපව චුම්භක වලලු ප්රසාරණය
වෙනවා හෝ හැකිලෙනවා.
ආකෘතියක්
වශයෙන් හා පැහැදිලි කිරීමේ
පහසුව තකා අප කියනවා චුම්භක
ක්ෂේත්රය (හෝ
වෙනත් ඕනෑම ක්ෂේත්රයක්)
සෑදී
තිබෙන්නේ බල රේඛාවලින් කියා.
ඉහත
රූපවල චුම්භක ක්ෂේත්රයන්
ඉරි හෝ රවුම්වලින් දක්වා ඇත්තේ
මෙම චුම්භක බල රේඛා තමයි.
ඇත්ත
වශයෙන්ම එම චුම්භක ක්ෂේත්ර
වලල්ල තුල මෙලෙස චුම්භක රේඛා
අනන්ත ගණනක් තිබෙනවා කියා
උපකල්පනය කළ හැකියි.
හරි,
දැන්
යම් චුම්භක ක්ෂේත්රයක් තුළ
සන්නායකයක් ඇතැයි සිතන්න.
චුම්භක
ක්ෂේත්රය හා කම්බිය අතර
සාපේක්ෂ චලිතයක් ඇති නොවේ
නම් හා චුම්භක ක්ෂේත්රය
විචලනය නොවේ නම්,
ඇත්තටම
මෙහිදී කිසිවක් අමුතු දෙයක්
සිදු නොවේ.
සටහන
යම් A හා B යන දෙකක් අතර සාපේක්ෂ චලිතයක් ඇති වෙනවා යනුවෙන් කී විට ඉන් හැඟවෙන්නේ කුමක්ද? එක්කෝ A නිශ්චලව තිබියදී B වලනය වේ. නැතහොත් B නිශ්චලව තිබියදී A චලනය වේ. නැතහොත් දෙකම එකවර චලනය වේ. ඒ කියන්නේ දෙකෙන් එකක සිට බලන විට අනෙක චලනය වනවා සේ දැනිය යුතුය. ඔබ වාහනයක ගමන් කරන විට, ඔබට පේනවා ගස් ගෙවල් ආදිය ඔබට සාපේක්ෂව පසුපසට යනවා සේ. සත්ය ලෙසම ඔබයි ඒවාට සාපේක්ෂව ඉදිරියට යන්නේ. කුමක් ගමන් කළත් කමක් නැහැ; සාපේක්ෂ චලිතයේදී වැදගත් වන්නේ එකක් අනෙකට සාපේක්ෂව චලනය වීමයි.
යම් A හා B යන දෙකක් අතර සාපේක්ෂ චලිතයක් ඇති වෙනවා යනුවෙන් කී විට ඉන් හැඟවෙන්නේ කුමක්ද? එක්කෝ A නිශ්චලව තිබියදී B වලනය වේ. නැතහොත් B නිශ්චලව තිබියදී A චලනය වේ. නැතහොත් දෙකම එකවර චලනය වේ. ඒ කියන්නේ දෙකෙන් එකක සිට බලන විට අනෙක චලනය වනවා සේ දැනිය යුතුය. ඔබ වාහනයක ගමන් කරන විට, ඔබට පේනවා ගස් ගෙවල් ආදිය ඔබට සාපේක්ෂව පසුපසට යනවා සේ. සත්ය ලෙසම ඔබයි ඒවාට සාපේක්ෂව ඉදිරියට යන්නේ. කුමක් ගමන් කළත් කමක් නැහැ; සාපේක්ෂ චලිතයේදී වැදගත් වන්නේ එකක් අනෙකට සාපේක්ෂව චලනය වීමයි.
එහෙත්
එක්කෝ චුම්භක ක්ෂේත්රය විචලනය
වේ නම්;
නැතහොත්
ඒ දෙක අතර සාපේක්ෂ චලිතයක්
ඇති වේ නම්,
විද්යුත්
ප්රේරණය නම් සංසිද්ධිය සිදු
වේ.
ඒ
කියන්නේ ක්ෂේත්රය තුළ තිබෙන
සන්නායකයේ අමුතුවෙන් විදුලි
ශක්තියක් උත්පාදනය වේ.
මෙහිදී
එම කම්බියට කොහෙන්වත් විදුලියක්
ගෙනත් දුන්නේ නැත;
තමන්
විසින්ම විදුලියක් උත්පාදනය
කරගත්තා.
හොඳින්
මතක තබා ගන්න මෙලෙස ප්රේරිත
විදුලයක් හටගැනීමට නම්
අනිවාර්යෙන්ම ක්ෂේත්රය හා
සන්නායකය අතර සාපේක්ෂ චලිතයක්
සිදු විය යුතුය නැතිනම් චුම්භක
ක්ෂේත්රය විචලනය විය යුතුය.
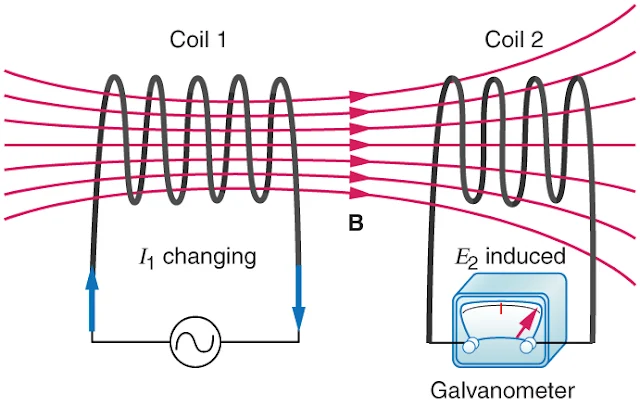
පහත
රූපයේ දැක්වෙන්නේ coil
1 හි
විචලනය වන විදුලියක් ගමන්
කරන විට,
ඊට
අනුරූපව විචලනය වන චුම්භක
ක්ෂේත්රයක් ඇති වී,
එම
විචලනය වන චුම්භක ක්ෂේත්රය
coil
2 හි
කැපීමෙන් එහි ප්රේරිත විදුලියක්
හටගනී.
(ගැල්වනොමීටරය
මඟින් එම ප්රේරිත ධාරාවේ
ප්රමාණය මැනගත හැකියි.)
ඇත්තටම මෙලෙස හේතු/සාධක දෙකක් පෙන්නුවත් මෙතැන තිබෙන්නේ එකම හේතුවකි/සාධකයකි. මේ දෙකම එකක් බව පහසුවෙන් තේරෙනවා ක්ෂේත්රය පුරාම තිබෙන්නේ චුම්භක බල රේඛා බව සිතුවොත්. ප්රේරණය සිදු වන්නේ චුම්භක බල රේඛා සන්නායකයක් විසින් කැපීමේදිය. දැන් නැවතත් අර සාධක දෙක ගැන බලමු.
චුම්භක
ක්ෂේත්රය තුළ තිබෙන සන්නායකය
චලනය වන අවස්ථාවේදී එම සන්නායකය
විසින් බල රේඛා කපනවා.
හරියට
සුළං හමන විට ඔබ එම සුළඟට මුහුණ
දෙමින් දුවනවා වාගේ (එවිට
ඔබට දැනෙනවා සුළං රැළි ඔබේ
ශරීරයේ වදිනවා).
ඇත්තටම
මෙහිදී සන්නායකය ක්ෂේත්රය
තුල චලනය විය යුත්තේ බල රේඛා
කැපෙන පරිදියි.
බල
රේඛා නොකැපෙන පරිදිත් චලනය
විය හැකියි.
එවිට
විදුලියක් ප්රේරණය නොවේ.
උපමාවකින්
මෙය කදිමට පැහැදිලි කර ගත
හැකියි.
සිතන්න
ඔබ වටා තවත් මිනිසුන් රාශියක
රැස්ව සිටිනවා කියා.
එවිට
ඔබට ඔබේ අත හරහාට සොලවන්නට
බැහැ මොකද අනිත් අයගේ ඇඟේ වදින
නිසා.
එහෙත්
අනිත් අයගේ ඇඟේ නොවදින ලෙසටත්
අත් සෙලවිය හැකියි උඩට හා පහලට
සෙලවීමෙන්.
එලෙසම
ක්ෂේත්රය හරහා සන්නායකය
චලනය වන විටයි බල රේඛා කැපෙන්නේ.
සන්නායකය
ක්ෂේත්රය තුළ ඉහල පහල චලනය
වන විට බල රේඛා නොකැපේ.
දෙවැනි
සාධකය බලමු.
ක්ෂේත්රය
විචලනය වෙන විට (එනම්
ක්ෂේත්රයේ වලලු වරින් වර
ප්රසාරණය වීම හා සංකෝචනය
වීම),
එවිටද
සන්නායකය කපාගෙන වලලු/බල
රේඛා විචලනය වේ.
දැක්කද
මේ සාධක දෙකෙන්ම සිදුවන්නේ
එකම දෙය වන බල රේඛා කැපීමයි.
චුම්භකයක්
හා සන්නායකයක් අතර සාපේක්ෂ
චලිතයක් ඇති කර එමඟින් විදුලියක්
උත්පාදනය කිරීමේ උපක්රමයට
තමයි අප විදුලි ජෙනරේටර් කියා
කියන්නේ.
එහෙත්
මෙය ඉලෙක්ට්රොනික්ස් පාඩමක්
නිසා ජෙනරේටර් ගැන දැනට පැහැදිලි
කරන්නට යන්නේ නැත (එය
අයත් වන්නේ ඉලෙක්ට්රිකල්
ක්ෂේත්රයටයි).
මේ
අනුව,
ඉලෙක්ට්රොනික්ස්වල
ඉන්ඩක්ටර් පාඩමට අවශ්ය වන්නේ
විචලනය වන ක්ෂේත්රය නම්
සාධකයයි.
සාමාන්ය
කාන්දම් කෑලිවල තිබෙන චුම්භක
ක්ෂේත්රය අපට ඕන ඕන විදියට
විචලනය කළ නොහැකියි.
එම
ක්ෂේත්ර බොහෝදුරට ස්ථාවරයි.
එහෙත්
විද්යුත් චුම්භකවල ක්ෂේත්රය
පහසුවෙන් අපට ඕන ඕන විදියටත්
ඉතා ක්ෂණයකිනුත් විචලනය කරන්නට
හැකියි.
කරන්නට
තිබෙන්නේ විද්යුත් චුම්භකය
හරහා ගලන ධාරාව අපට ඕන ඕන විදියට
විචලනය කිරීම පමණයි.
දැන්
මෙම විද්යුත් චුම්භකය හරහා
ගලන ධාරාව විචලනය කරන්න.
එවිට,
එහි
හටගන්නා විචලනය සහිත ක්ෂේත්රය
තුළ සන්නායක කම්බියක් තැබූ
විට,
එම
කම්බියේ විදුලියක් හට
ගන්නවා/ප්රේරණය
වෙනවා.
එක්
කම්බියක් තුළින් විචලනය වන
විදුලියක් යවන විට අනෙක් අසල
ඇති කම්බියේ විදුලියක් හට
ගැනීම හඳුන්වන්නේ "අන්යොන්ය
ප්රේරණය"
(mutual induction) ලෙසයි.
ට්රාන්ස්ෆෝමර්
යනු අන්යොන්ය ප්රේරණය මත
සාදා තිබෙන උපාංගයකි.
ධාරාව
යවා විද්යුත් චුම්භකය බවට
පත් කළ පළමු සන්නායකය "ප්රේරක
කොයිල් එක"
හෙවත්
"ප්රාථමික
කොයිලය"
(primary coil) ලෙස
හැඳින් විය හැකියි.
විදුලිය
උත්පාදනය වන අනෙක් සන්නායකය
"ද්විතියික
කොයිලය"
(secondary coil) ලෙස
හැඳින් විය හැකියි.
ඉහත
රූපය බලන්න.
මෙලෙස
ප්රේරණය වන විදුලිය වැඩි
කිරීමට ක්රම දෙකක් තිබේ.
එකක්
නම් ක්ෂේත්රය ප්රබල කිරීමයි.
මේ
සඳහා ප්රාථමික සන්නායකය
හරහා ගලා යන ධාරාව වැඩි කළ
හැකියි.
ඊට
අමතරව ප්රාථමික සන්නායකයේ
පොටවල් ගණනද වැඩි කළ හැකියි.
දෙවැන්න
වන්නේ ප්රාථමිකයේ විචලනය
වන විදුලියේ සංඛ්යාතය ඉහල
දැමීමයි.
මෙම
කාරණා Faraday
නම්
විද්යාඥයා විසින් පර්යේෂණාත්මව
සොයා ගන්නා ලදි.
එය
සූත්රයක් ලෙස ෆැරඩේ සූත්රය
නමින් පහත ආකාරයට ලිවිය හැකියි.
ද්විතියකයේ
ප්රේරණය වන විදුලි විභවය =
(ද්විතියිකයේ
පොටවල් ගණන)x(ප්රාථමිකයේ
විචලනය වන විදුලිය නිසා චුම්භක
ක්ෂේත්රය විචලනය වන වේගයේ
සංඛ්යාතය)
කෙටියෙන් එය,
ලෙස ලියනවා.
මෙම
ෆැරඩේ සූත්රයෙන් ලැබෙන්නේ
ද්විතියකයේ උත්පාදනය වන
විදුලියේ විභවයයි.
N යනු
ද්විතියිකයේ පොටවල් ගණන වන
අතර වරහන තුළ තිබෙන කොටස
දක්වා ඇත්තේ අවකලනය නම් ගණිත
නිරූපණ ක්රමය අනුවයි.
කාලයට
සාපේක්ෂව චුම්භක ක්ෂේත්රයේ
විචලන සංඛ්යාතය ඉන් නිරූපණය
කෙරේ.
සමහර
අවස්ථාවල N
(පොටවල්
ගණන)
ඉහත
සූත්රයෙන් ඉවත් කරද දක්වනවා;
එවිට
එය එක් පොටක් සඳහා වන සූත්රය
බව සිහිතබා ගන්න.
අවස්ථා
කිහිපයකම පෙන්වා දුන්නා පොටවල්
(එනම්
සන්නායක කම්බි)
ගණන
වැඩි කරන විට ප්රේරණ ගුණය
වැඩි වන බව.
මෙහිදී
ප්රායෝගිකව පොටවල් ගණන වැඩි
කරන්නේ කම්බි/වයර්
ගොන්නක් (අර
දර මිටියක් සේ)
එකට
ගැනීමෙන් නොව.
ඊට වඩා
පහසු කාර්යක්ෂම ක්රමය නම්
එය පහත රූප දෙකේ දැක්වෙන සේ
දඟරයක් (coil)
සේ
සකස් කිරීමයි.
මින්
එක් දඟර ක්රමයක් solenoid
(සොලනොයිඩ්)
ලෙස
හැඳින් වෙන අතර,
අනෙක්
දඟර ක්රමය torroid
(ටොරොයිඩ්)
ලෙස
හැඳින්වෙනවා.
කොයිල්
එකක එක් සම්පූර්ණ වටයක් එක
පොටක් සේ සැලකෙනවා.
ඒ අනුව,
දඟරයේ
වට 100ක්
ඇත්නම්,
පොටවල්
100ක්
ඇතැයි සැලකෙනවා.
ඍජු
කම්බියක විද්යුත් චුම්භකයක්
සෑදෙන විට,
එය
රවුම් රවුම් සේ පවතී (චුම්භක
මුදු).
මෙවිට
චුම්භක උතුර-දකුණ
නිශ්චිතවම සෙවිය නොහැකියි
(මුදුවේ
එක් තැනක් උතුර ලෙස සැලකුවොත්,
ඊට
හරියටම අංශක 180ක්
ගිය තැන දකුණ ලෙස සැලකීමට සිදු
වේ).
එහෙත්
කොයිලයක් සැලකීමේදී එක් එක්
කොයිල් වටයේ චුම්භක මුදු එකතු
වී (අධිස්ථාපනය
වී)
පහත
රූපවල පෙන්වා ඇති පරිදි ඍජු
චුම්භක රේඛා ඇති වේ (මුදු
ලෙස නොව).
හරියටම
කාන්දම් කෑලිවල චුම්භක රේඛා
පවතින්නෙත් කොයිල්වල පවතින
විදියටමයි.
ඒ
කියන්නේ ධාරාව ඍජුව ගමන් කරන
විට,
චුම්භක
රේඛා පිහිටන්නේ රවුමට (මුදු
ආකාරයට)
වන
අතර,
ධාරාව
රවුමට ගමන් කරන විට,
චුම්භක
රේඛා පිහිටන්නේ ඍජුව වේ.
ද්විතියිකය තුළ යම් විදුලි විභවයක් හට ගන්නවා යනු එය හරහා යම් ධාරාවක්ද හට ගන්නවා කියන එකයි. එම ධාරාව ඕම් නියමය අනුව ඔබට නිර්ණය කළ හැකියි (වෝල්ටියතාව හා ද්විතියිකයේ ප්රතිරෝධය දන්නා නිසා).
මෙම
ධාරාව ගලා යන දිශාවද වැදගත්.
එම
ප්රේරිත ධාරාවේ (induced
current) දිශාව
නිර්ණය කරන්නේ කෙලෙසද?
මේ
සඳහා සරල නියමයක් තිබෙනවා
Lenz's
Law (ලෙන්ස්
නියමය)
ලෙස.
එය
මෙසේ පැහැදිලි කළ හැකියි.
මුල්
ධාරාව විසින් චුම්භක ක්ෂේත්රයක්
සාදනවා.
එම
ක්ෂේත්රය විසින් ප්රේරිත
ධාරාව නිපදවනවා.
එම
ප්රේරිත ධාරාව ගමන් කරන විට,
නැවතත්
චුම්භක ක්ෂේත්රයක් ඊට අනුරූපව
ජනිත වෙනවා.
එවිට,
චුම්භක
ක්ෂේත්ර දෙකක් දැන් පවතිනවා.
මෙම
චුම්භක ක්ෂේත්ර දෙක අතර අපූරු
අන්යොන්ය සම්බන්ධතාවක්
පවතිනවා (යාලුවො
දෙන්නෙක් වාගේ).
මුල්
ක්ෂේත්රය වෙනස් වන විට,
දෙවන
ක්ෂේත්රය හැමවිටම උත්සහ
කරනවා එම වෙනස අහෝසි කර දමන්න.
ඒ
කියන්නේ මුල් ක්ෂේත්රය
මොහොතකින් අඩු වෙනවා යැයි
සිතමු.
එවිට
දෙවැනි ක්ෂේත්රය එම අඩුවීම
වැලැක්වීමට ක්රියා කරනවා.
එලෙසම
මුල් ක්ෂේත්රය මොහොතකින්
වැඩි වෙනවා යැයි සිතමු.
එවිට
දෙවැනි ක්ෂේත්රය එම වැඩිවීම
වැලැක්වීමට උපක්රම යොදනවා.
එය
කරන්නේ කෙලෙසද?
හරිම
පහසුයි.
ක්ෂේත්රයක්
අඩු හෝ වැඩි කිරීමට ඇති හොඳම
ක්රමය ධාරාව අඩු වැඩි කිරීම
බව මුලදිත් සඳහන් කළා.
දැන්
මෙලෙස තර්ක කර බලන්න.
මුල්
ක්ෂේත්රය වැඩිවෙන අවස්ථාව
ගන්න.
එවිට
දෙවැනි ක්ෂේත්රය කෙසේ හැසිරිය
යුතුද?
දෙවැනි
ක්ෂේත්රයට කරන්නට තියෙන්නේ
පළමු ක්ෂේත්රයේ දිශාවට
විරුද්ධ දිශාවට තමන්ගේ ක්ෂේත්රය
පවත්වා ගන්නයි (විද්යුත්
ක්ෂේත්රය මෙන්ම චුම්භක
ක්ෂේත්රයද දෛශික රාශි වේ).
උදාහරණයක්
ලෙස ප්රාථමික කම්බියේ ධාරාව
ගලන්නේ යට සිට උඩට නම්,
දකුණත්
රීතිය අනුව චුම්භක වලලුවල
දිශාව වාමාවර්ත වේ.
එම
දිශාවටම වැඩිපුර ධාරාවක් ගලන
විට,
එම
ක්ෂේත්රය තවදුරටත් ප්රසාරණය
වන්නට උත්සහ කරනවා.
මේ
එක්කම අනෙක් කම්බියේද විදුලි
ධාරාවක් ගලා යනවා.
එනිසා
එය තුළත් චුම්භක ක්ෂේත්රයක්
හට ගන්නවා.
ඉහත
ලෙන්ස් නියමය අනුව මෙම අලුත්
ක්ෂේත්රය අර මුල් ක්ෂේත්රයේ
ප්රසාරණය වලක්වන විදියටයි
පිහිටන්නට ඕන.
ඒ
කියන්නේ මෙම අලුත් ක්ෂේත්රය
දක්ෂිණාවර්තව පිහිටිය යුතුයි
(දෙක
එකිනෙකට විරුද්ධ දිශාවලට
පිහිටන විටනේ එකිනෙකට කොටස්
කැපී යන්නෙ).
නැවත
දකුණත් රීතිය මෙම දෙවැනි
කම්බියට දැන් යොදන්න.
එවිට
ධාරාව ගලා යා යුත්තේ උඩ සිට
පහලට බව පෙනෙනවා.
මෙන්න
මේ විදියට තමයි ලෙන්ස් නියමය
මඟින් ප්රේරිත ධාරාවේ දිශාව
සෙවිය යුත්තේ.
මෙහිදී
ඔබ තැවෙන්න එපා දෙවැනි ක්ෂේත්රය
ඇත්තටම පළමු ක්ෂේත්රයට බලපෑම්
කරනවාද නැද්ද කියා.
මෙය
ආකෘතියක් පමණයි.
මෙලෙසම
දැන් තර්ක කර බලමු පළමු ක්ෂේත්රය
සංකෝචනය වන විට කුමක්ද සිදු
වන්නේ කියා.
නැවතත්
සිතන්න ප්රාථමික සන්නායකයේ
ධාරාව යට සිට උඩට ගමන් කරන බව.
එවිට
ක්ෂේත්රයේ වලලු පිහිටන්නේ
වාමාවර්තවයි.
දැන්
ප්රාථමිකය හරහා යන ධාරාව
අඩු වෙනවා යැයි සිතමු.
එවිට
ක්ෂේත්රය සංකෝචනය වන්නටයි
හදන්නේ.
එහෙත්
ද්විතියිකයේ ප්රේරිත චුම්භක
ක්ෂේත්රය උත්සහ කරන්නේ මෙම
සංකෝචනය නවතා දමන්නට.
ඒ සඳහා
කරන්නට තිබෙන්නේ අඩුවන ක්ෂේත්රය
ඊට ලබා දීමයි.
ඒ
කියන්නේ ද්විතියිකයේ ක්ෂේත්රයත්
ප්රාථමිකයේ ක්ෂේත්රයට එකතු
විය හැකි පරිදියි සැකසෙන්නේ.
ඒ
කියන්නේ ද්විතියික ක්ෂේත්රයත්
වාමාවර්තව සෑදෙනවා.
එමනිසා
දකුණත් නියමය අනුව,
ද්විතියිකයේ
හටගන්නා ධාරාවත් යට සිට උඩට
ගමන් කිරීමට සිදු වෙනවා.
ලෙන්ස්
නියමය අපූරුය.
එහෙත්
සමහරෙකුට එය කරදරයක් සේ දැනේ.
එවැනි
අයට මෙලෙස එය මතක තබා ගත හැකියි
අවශ්ය නම්.
චුම්භක
ක්ෂේත්රය වැඩිවන විට ප්රේරිත
ධාරාව ගලන්නේ මුල් ධාරාවට
විරුද්ධ දිශාවටයි.
ක්ෂේත්රය
අඩුවන විට,
ප්රේරිත
ධාරාව මුල් ධාරාවේ දිශාවටම
ගමන් කරයි.
එයම
මෙලෙසත් මතක තබා ගත හැකියි.
මුල්
ධාරාව වැඩි වන විට,
ප්රේරිත
ධාරාව මුල් ධාරාවේ දිශාවට
විරුද්ධ පැත්තට ගමන් කරන අතර,
මුල්
ධාරාව අඩුවන විට,
ප්රේරිත
ධාරාව මුල් ධාරාවේ දිශාවටම
ගමන් කරයි.
මෙහිදී
ප්රේරිත ධාරාව විසින් සිදු
කරන්නේ මුල් ධාරාව නියාමනය
කිරීමක් වැනි දෙයකි.
එනම්,
මුල්
ධාරාව වෙනස් වෙනවාට ප්රේරිත
ධාරාව කැමැති නැත.
ප්රේරිත
ධාරාව හොඳ ආදරවන්තයෙක්;
(මුල්
ධාරාව නම්)
පෙම්වතිය
වෙනස් වෙනවාට එයා කැමැති නැත.
ඉහත
විස්තරය කියවන විට ඔබට පහසුවෙන්ම
අන්යොන්ය ප්රේරණය අවබෝධ
කර ගත හැකියි.
එහෙත්
තවත් වර්ගයේ ප්රේරණයක්
තිබෙනවා "ස්වයං
ප්රේරණය"
(self induction) නමින්.
මෙය
තමයි (අප
මෙම පාඩමින් කතා කරමින් සිටින)
ප්රේරකවල
භාවිතා වන ප්රේරණ වර්ගය.
එකවරම
සමහරෙකුට මෙය අර තරම් පහසුවෙන්
තේරුම් ගන්නට අපහසු වේවි.
ස්වයං
ප්රේරණයේදී සන්නායක දෙකක්
අවශ්ය නැත.
ප්රේරණය
සිදු වන්නේද මුල් (ප්රාථමික)
දඟරයේමයි.
එහෙත්
ඉහත අන්යොන්ය ප්රේරණය ගැන
කියූ විස්තර එලෙසම මීටද වලංගු
වේ.
පෙර
සේම යම් සන්නායකයක් හරහා
විචලනය වන විදුලියක් යවනවා.
එමඟින්
විචලනය වන චුම්භක ක්ෂේත්රයක්
හටගන්නවා.
දැන්
එම චුම්භක ක්ෂේත්රයේ බල රේඛා
විසින් එම සන්නායකයම කපනවා
(හරියට
පෙර අවස්ථාවෙදී අසල තිබුණු
සන්නායකය කපනවා වාගේ).
එවිටත්
එම බල රේඛා කැපීම නිසා අලුතින්
විදුලියක් එම සන්නායකය තුල
උත්පාදනය වෙනවා.
ඔව්,
දැන්
එම සන්නායකය තුළ විදුලි ධාරාවන්
දෙකක් ගමන් කරනවා.
එකක්
නම්,
මුලින්ම
ගමන් කළ විදුලිය;
අනෙක
නම් ස්වයං-ප්රේරණය
නිසා අලුතින් ඇති වූ විදුලියයි.
මෙම
ධාරා දෙක හැසිරෙන ආකාරය තමයි
ඉන්ඩක්ටරයේ ක්රියාකාරිත්වය
පිටුපස තිබෙන රහස.
දැන්
තවදුරටත් ප්රේරණතාව ගැන
සලකා බලමු.
පළමුව,
අන්යොන්ය
ප්රේරණතාව ගැන බලමු (අන්යොන්ය
ප්රේරණය අප ඉලෙක්ට්රොනික්ස්වල
යොදන ප්රේරකවලට වැදගත්
නොවුණත් මේ ගැන දැන සිටීම
අනෙක් කාරණා අවබෝධ කර ගැනීමට
පහසුය).
අන්යොන්ය
ප්රේරණය (mutual
induction) යනු
ප්රාථමික කොයිලය තුළින් යම්
ධාරාවක් ගලන විට,
ද්විතියකයේ
කොතරම් චුම්භක ක්ෂේත්රයක්
(හෝ
ස්රාවයක්)
ඇති
වෙනවාද යන්නයි.
එ්
අනුව,
ප්රාථමිකයේ
ධාරාවට සමානුපාතිකයි ද්විතියිකයේ
චුම්භක ස්රාවය (magnetic
flux). සමානුපාතිකයක්
සමාන කිරීම ගණිතානුකූලව සිදු
කරන ආකාරය නම් යම් නියතයක්
(constant)
යෙදීමයි.
මෙන්න
මෙම නියතය තමයි "අන්යොන්ය
ප්රේරණතාව"
(mutual inductance) ලෙස
හැඳින්වෙන්නේ.
ψ
∞ I (චුම්භක
ස්රාවය සමානුපාතිකයි ධාරාවට)
ψ = MI (M යනු අන්යොන්ය ප්රේරණතාවයි)
ψ = MI (M යනු අන්යොන්ය ප්රේරණතාවයි)
එහෙත්
අපට චුම්භක ස්රාවයකින් එතරම්
ප්රයෝජනවත් නැත.
ඉහතදී
පෙන්වා දුන් ෆැරඩේ නියමය අනුව
අපට චුම්භක ස්රාවය විභවයකට
පරිවර්ථනය කළ හැකියි (ස්රාවය/කාලය
=
විභවය
නිසා).
ඒ අනුව
අපට ඉහත සූත්රයම පහත වඩා
ප්රයෝජනවත් ආකාරයට සකස් කළ
හැකියි.
ඉහත
සූත්රය වචනයෙන් මෙසේ කිව
හැකියි.
ප්රාථමිකයේ
ධාරාවේ වෙනස් වීමේ සීඝ්රතාවට
සමානුපාතිකව ද්විතියිකයේ
ප්රේරිත විභවය පවතී.
මේ
අනුව,
ප්රාථමිකයේ
එක් තත්පරයක් තුළදී ධාරාව
ඈම්ප් එකකින් වෙනස් වන විට,
ද්විතියිකයේ
වෝල්ට් එකක් හට ගත්තේ නම්,
එහි
අන්යොන්ය ප්රේරණතාව හෙන්රි
එකකි (1
= M (1/1) → M = 1 Henry).
දැන්
අපට පහසුවෙන්ම අපට වැදගත්
ස්වයං-ප්රේරණතාව
අවබෝධ කර ගත හැකියි.
ස්වයං-ප්රේරණතාව
යනු කොයිලය තුළ යම් ධාරාවක්
ගමන් කරන විට,
එහි
ප්රතිඵලයක් ලෙස එම කොයිලයේම
සමානුපාතිකව ඇතිවන චුම්භක
ස්රාවය කොපමණද යන්නයි.
ψ
∞ I (චුම්භක
ස්රාවය සමානුපාතිකයි ධාරාවට)
ψ = LI (L යනු ස්වයං-ප්රේරණතාවයි)
ψ = LI (L යනු ස්වයං-ප්රේරණතාවයි)
පෙර
ලෙසම ස්රාවයට වඩා විභවය
ප්රයෝජනවත් නිසා විභවය
ඇසුරින් ඉහත සූත්රය පහත
ආකාරයට ලිවිය හැකියි.
මේ
අනුව,
කොයිලයේ
තත්පර එකක් තුළ ඇම්පියර් එකක
වෙනසක් සිදු වන විට,
එම
කොයිලයේම වෝල්ට් එකක් ප්රේරණය
වන විට,
ස්වයං-ප්රේරණතාව
හෙන්රි එකකි.
ස්වයං-ප්රේරණතාව
තමයි අප මෙම ඉලෙක්ට්රොනික්
පාඩම් මාලාවට මින් ඉදිරියට
පදනම් කර ගන්නේ.
ඉලෙක්ට්රෝනික්ස් (electronics) ...
ඉලෙක්ට්රෝනික්ස් (electronics) ...









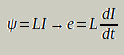
Sir,
ReplyDeleteබොහොම ස්තුතියි ඔබේ ලිපියට.මට පොඩි ප්රශ්නයක් තියෙනවා.
ඇයි මේ සූත්රේ L(ස්වයං-ප්රේරණතාව) රින ලකුණකින් ගුණ වෙලා තියෙන්නේ ?
E = -L*I/t
මගේ පොතේ ඇති සටහනට අනුව එය මෙසේ සදහන්ව ඇත.එහෙත් මට එය පැහැදිලි නැත.
"රින ලකුණින් ප්රකාශවනුයේ ප්රේරකයේ උපදින විද්යුත් ගාමක බලය සැපයුම් වෝල්ටීයතාවයේ දිශාවට විරුද්ධව ඇතිවන බවයි"
විද්යුත් ගාමක බලය සැපයුම් වෝල්ටීයතාවයේ දිශාවට විරුද්ධව ඇතිවන්නේ කෙසේද ?
සර්ගේ සටහනට අනුව ඒ ප්රේරකය තුලින් ගලන ධාරාව වැඩිවන විටයි.
එහෙත් ප්රේරකය තුලින් ගලන ධාරාව අඩුවන විට මෙම රින ලකුණ සූත්රයෙන් ඉවත් වන්නේද ?
මෙය මට පැහැදිලි කරදෙන්න.
මෙහි ඍණ ලකුණ ප්රේරණතාවට අයත් එකක් නොව, = ලකුණට පසුව ඇති සමස්ථ ප්රකාශයටම අයත් එකකි. ඉන් අදහස් වන්නේ ප්රේරණතාවෙන් උත්පාදනය වන මෙම විදුලිය එම ප්රේරණතාව ඇති කළ විදුලියට ප්රතිවිරුද්ධ දිශාව ඔස්සේ පවතින බවකි. ඍණ ලකුණින් හැඟවූයේ එයයි. මා එය පාඩම තුල සඳහන් කර තිබෙනවා.
Deleteවිදුලිය යන වචනය යොදා ගන්නා විට, ධාරාව හා විභවය යන දෙකම හෝ දෙකින් එකක් සාමාන්යයෙන් ගම්ය වෙනවා (සංදර්භය අනුව එය පහසුවෙන්ම වැටහෙනවා විදුලිය ගැන දැනුමක් තිබෙන විට). ඒ අනුව එම ප්රකාශය තේරුම් ගත යුත්තේ මෙසේය. ප්රේරණය නිසා හටගත් විදුලි ධාරාව ගලන්නේ එය ප්රේරණය කිරීමට හේතු වූ මුල් ධාරාවට විරුද්ධ දිශාවටයි.
ප්රේරිත විදුලි විභවය (විද්යූත් ගාමක බලය) කියන්නේ එක් විදුලියක්, ඔරිජිනල් විදුලිය කියන්නේ තවත් විදුලියක්. ඉතිං ඒ දෙක එකම වයරය තුල දෙදිශාවකට පිහිටිය හැකියි. එහි ගැටලුවක් නැත.
ඍණ ලකුනින් කියන්නේ දිශාව විරුද්ධ බවයි (ගණිතානුකූලව සිතා බලන්න). ඍණ ලකුණ ගැන අමුතුවෙන් සිතන්න එපා. එම විදුලිය මුල් විදුලියට විරුද්ධව පවතින බව සිතන්නට පුරුදු වෙන්න. ඉතිං, ඔරිජිනල් විදුලිය අඩු වන විට ප්රේරණ විදුලිය අඩු වේ (ඇත්තටම විදුලිය විචලනය වන සීග්රතාවයි වැදගත් වන්නේ). ප්රේරිත විදුලිය 0 වෙනවා මුල් ධාරාව 0 වන විට.
සර් බොහොම ස්තුතියි ඔබේ පැහැදිලි කරදීමට.ඔබේ බ්ලොග් එකෙන් බොහෝ දේ ඉගෙනගත්තා. තව බොහෝ කාලයක් මේ බ්ලොග් එක ලියන්න.
Delete:)
Deleteඔබ ඇසූ ප්රශ්නය දැනුයි මට හරියටම තේරුණේ. මා ඉහත දී තිබෙන පිලිතුර තවදුරටත් මෙසේ විස්තර කිරීමට සිදු වෙනවා. මුල්/ඔරිජිනල් ධාරාවට "හතුරෙකු" සේ හැමවිටම ප්රේරිත ධාරාව හැසිරෙනවා. ඒ අනුව මුල් ධාරාව වැඩි වන විට එම වැඩි වීම වැලැක්වීමට ප්රේරිත ධාරාව ක්රියා කරනවා. ඉතිං කොහොමද එය කළ හැක්කේ? මුල් ධාරාවට ප්රතිවිරුද්ධ දිශාවට ප්රේරිත ධාරාව යැවීමෙන් එය කළ හැකියිනෙ. එලෙසම, මුල් ධාරාව අඩු වන විටත් ප්රේරිත ධාරාව එය වැලැක්වීමට ක්රියා කරනවා. එය කළ හැක්කේ කෙසේද? මුල් ධාරාව පැත්තටම ප්රේරිත ධාරාව ගමන් කරවීමෙන් එය කළ හැකියි. මෙම සතුරුකම හැඟවීමට තමයි ඍණ ලකුණ පවතින්නේ. කෙසේ වෙතත් මුල් ධාරාව ගමන් කිරීම ආරම්භ කරන අවස්ථාවේදීම ප්රේරිත ධාරාව ඊට ප්රතිවිරුද්ධ දිශාවට පවතිනවා (ඉහත කමෙන්ටුවේ මා අවධානය දී තිබෙන්නේ එම කොටසට පමණක් බව දැනුයි දැක්කේ).
Delete