ඕනෑම
සන්නායකයක්/වයරයක්/කම්බියක්
ගත් විට,
එය
ඉබේම ඉන්ඩක්ටරයක් සේ ක්රියා
කරනවා.
කිසිසේත්
එය වැලැක්විය නොහැකියි.
එය ඔබට
සිතාගත හැකියිනෙ.
එනම්,
ධාරාවක්
ගමන් කරන විට,
අනිවාර්යෙන්ම
එහි චුම්භක ක්ෂේත්රයක් හට
ගන්න අතර,
එම
ධාරාව විචලනය වන විට,
ස්වයං-ප්රේරණය
එතුල සිදු වේ.
එහෙත්
එවැනි තනි පොටක් සහිත වයර්
එකක පවතින ඉන්ඩක්ටන්ස් එක
ඉතාම කුඩාය.
සාමාන්ය
පරිපථවලදී එය කිසිසේත් ගණන්
ගන්නේ නැත.
පොටවල්
ගණන වැඩි කරන විට (එනම්
කොයිල් එකක් ලෙස සෑදීමෙන්)
හා
තවත් උපක්රම මඟින් ඉන්ඩක්ටන්ස්
එක වැඩි කර ගත හැකියි (මේ
ගැන මොහොතකින් විමසමු).
ඉන්ඩක්ටන්ස්
එක වැඩි කිරීමට යොදා ගන්නා
උපක්රමය අනුව ඉන්ඩක්ටර් එක
සඳහා යොදා ගන්නා සංඛේත හතරක්
පමණ ඇත.
පහත
දැක්වෙන්නේ ඉන්ඩක්ටර් සඳහා
සම්මත සංඛේතයි.
ඇඳීමේ
පහසුව පිණිස සමහරවිට පළමු
සංඛේතය පොදුවේ භාවිතා වෙනවා.
අනෙක් උපාංග මෙන්ම ඉන්ඩක්ටර්ද ශ්රේණිගතව හා සමාන්තරගතව සම්බන්ධ කළ හැකියි. ප්රතිරෝධකවල සූත්රවලට අනුරූප සූත්ර පවතී. එනම්, ශ්රේණිගතව සම්බන්ධ කරන විට, නිකංම ඉන්ඩක්ටර් අගයන් එකතු වන අතර, සමාන්තරගතව සම්බන්ධ වන විට, ඒ උපාංගවල පරස්පරයන්ගේ එකතුව සමක ප්රතිරෝධකයේ පරස්පරයට සමාන වේ.
ශ්රේණිගත
සම්බන්ධය සඳහා
LT
= L1 + L2 + L3 + …
මෙය සාධනය කිරීම ඉතා පහසුය. ධාරිත්රක සඳහා Q = CV යන සූත්රය පවතින්නා සේ, ප්රේරක සඳහා e = L(dI/dt) සූත්රය පවතී. මෙම සූත්රය ඉහත එක් එක් ප්රේරකයට යොදන්න මොකද ප්රේරක සියල්ලෙහිම වෝල්ටියතාවන්ගේ එකතුව භාහිර වෝල්ටියතාවට සමාන වේ. තවද, මේ සියල්ලම තුලින් ගලා යන්නේ එකම ධාරාව වන අතර එම ධාරාව විචලනය වන සංඛ්යාතය මේ සියල්ලටම පොදු වේ. මේ අනුව,
Vs
= e1 + e2 + …
LT(dI/dt) = L1(dI/dt) + L2(dI/dt) + …
LT = L1 + L2 + ...
LT(dI/dt) = L1(dI/dt) + L2(dI/dt) + …
LT = L1 + L2 + ...
සමාන්තරගත
සම්බන්ධය සඳහා
1/LT
= 1/L1 + 1/L2 + 1/L3 + …
ඇත්තටම මෙහි තත්වය එතරම්ම සරල නැත. ඊට හේතුව ඉන්ඩක්ටරයකින් ඇතිවන චුම්භක ක්ෂේත්රය තරමක් ඈතට විහිදීමයි. එවිට ළඟපාතක ඇති උපාංගවලට බලපෑමක් ඇති වේ. එනම්, යම් A නම් ඉන්ඩක්ටරයක් තවත් B ඉන්ඩක්ටරයක් සමීපයේ පවතිනවා යැයි සිතන්න. ඒ ඉන්ඩක්ටර් දෙක ශ්රේණිගතව හෝ සමාන්තරගතව එකිනෙකට සම්බන්ධව තිබිය හැකියි. එහෙමත් නැතිනම් එකිනෙකට සම්බන්ධ නොවී සර්කිට් එකේ ස්ථාන දෙකක පවතින ස්වාධීන ඉන්ඩක්ටර් දෙකක් වුවද විය හැකියි. කෙසේ හෝ වේවා එම ඉන්ඩක්ටර් දෙක කොතරම් සමීපයේ පවතිනවාද කිව්වොත් එක් ඉන්ඩක්ටරයක ක්ෂේත්රය අනෙක් ඉන්ඩක්ටරය කපයි. එවිට අපට අවශ්ය නොවූ අන්යොන්ය ප්රේරණයක් ඇති වෙනවා.
එකිනෙකට (ශ්රේණිගතව හෝ සමාන්තරගතව) සම්බන්ධිත ඉන්ඩක්ටර් දෙකක් නම්, ඉහත ශ්රේණිගත හා සමාන්තරගත සූත්ර දෙක පහත ආකාරයට වෙනස් වේ. මෙහිදී සිදු කරන්නේ අන්යොන්ය ප්රේරණ දෙක එම සූත්රවලට ඇතුලු කිරීමයි.
ශ්රේණිගත
අවස්ථාව සඳහා:
LT
= (L1 + M) + (L2 + M) = L1 + L2
+ 2M හෝ
LT
= (L1 - M) + (L2 – M) = L1 + L2
- 2M
ඉහත
දැක්වූ ලෙසට ඒ සඳහා සූත්ර
දෙකක් ලැබුණේ කෙසේද?
කොයිල්
ඔතා තිබෙන දිශාව අනුව (හෝ
කොයිල් දෙක එකිනෙකට සම්බන්ධ
කර තිබෙන විදිය අනුව)
එය
තීරණය වේ.
කොයිලය
ඔතා තිබෙන දිශාව (එනම්,
කොයිලයේ
ධාරාව ගමන් කරන දිශාව)
අනුවයි
ඉන් ඇතිවන ක්ෂේත්රයේ දිශාව
(උතුර-දකුණ)
තීරණය
වන්නේ.
ඉතිං,
කොයිල්
දෙකේම ක්ෂේත්ර දෙක එකම දිශාවට
වන සේ නම් ළඟින් ඇත්තේ එමඟින්
ඇතිවන අන්යොන්ය ප්රේරණ
දෙක එම කොයිල්වල ස්වයං-ප්රේරණ
දෙකට එකතු වේ.
එම
අවස්ථාව තමයි ඉහත පළමු සූත්රයෙන්
නිරූපණය වන්නේ (පහත
රූපයේ B
අවස්ථාව).
එලෙසම
කොයිල් දෙකෙහි ක්ෂේත්ර
එකිනෙකට විරුද්ධව ඇතිවන සේ
පවතී නම්,
අන්යොන්ය
ප්රේරණය ඉහත දෙවැනි සූත්රයේ
පෙන්වා දී තිබෙන පරිදි අඩු
කළ යුතුය (පහත
රූපයේ A
අවස්ථාව).
දකුණත්
නියමය යොදමින් ක්ෂේත්රයේ
දිශාව ඔබට පහසුවෙන් සෙවිය
හැකියි.
සමාන්තරගත
අවස්ථාව සඳහා:
1/LT
= 1/(L1 - M) + 1/(L2 – M) හෝ
1/LT = 1/(L1+M) + 1/(L2 + M)
1/LT = 1/(L1+M) + 1/(L2 + M)
ශ්රේණිගත
අවස්ථාවේදී එක් එක් ඉන්ඩක්ටන්ස්
එකට අන්යොන්ය ප්රේරණය අඩු
හෝ එකතු කළා සේ,
මෙහිදී
ඒ ඒ ඉන්ඩක්ටන්ස් එකෙන් අන්යොන්ය
ප්රේරණය අඩු හෝ එකතු කෙරේ.
කොයිල්
දෙකේ ක්ෂේත්රයන් එකිනෙකට
එකතු වෙන විදියට තිබුණොත්
එකතු කිරීමද,
එකිනෙකට
කැපෙන විදියට තිබුණොත් අඩු
කිරීමද සිදු කළ යුතුය.
එකිනෙකට
ඍජුව සම්බන්ධ නැති කොයිල්
දෙකක් ගැන සැලකීමේදිත් එහිද
ඇති වන්නේ අන්යොන්ය ප්රේරණයක්
වුවද,
එහිදී
වෙනස් ආකාරයකින් එය විග්රහ
කිරීමට සිදු වෙනවා.
එනම්,
මෙම
අවස්ථාවේදී ඇතිවන අන්යොන්ය
ප්රේරණය විශාල කරදරයක් ලෙස
සැලකිය යුතුයි.
මෙය
interference
අවස්ථාවකි
(මතකද
ධාරිත්රක ගැන කතා කරන විටත්
ඉන්ටර්ෆරන්ස් ගැන කතා කළා).
ධාරිත්රකවලට
වඩා සිය දහස් ගුණයකින් මෙලෙස
කොයිල් නිසා ඇතිවන ඉන්ටර්ෆරන්ස්
කරදරයකි.
එක්
කොයිලයක් හරහා යන සංඥාවක්
අනෙක් කොයිලයට කාන්දු වීම
බරපතල ප්රශ්නයක්නෙ.
මෙම
ඉන්ටර්ෆරන්ස් එක inductive
coupling ලෙස
හැඳින්වේ.
එහෙත්
මතක තබා ගන්න ශ්රේණිගතව හෝ
සමාන්තරගතව සම්බන්ධිත කොයිල්
දෙකකදී සිදුවන අන්යොන්ය
ප්රේරණය කිසිසේත් ඉන්ටර්ෆර්න්ස්
එකක් නොවේ මොකද හැමවිටම එම
කොයිල් දෙක හරහාම යන්නේ එකම
සංඥාව බැවින්.
එහෙත්
ඒකෙන් කියන්නෙ නැහැ එම අන්යොන්ය
ප්රේරණය කරදරයක් නොවේය කියා.
එමනිසා
ඉන්ටර්ෆරන්ස් එකක් ඇතිව හෝ
නැතිව ඇතිවන මෙම අන්යොන්ය
ප්රේරණය හැකි තරම් අවම කළ
යුතුය.
ඒ සඳහා
යම් උපක්රමයක් ඇත.
හැකි
පමණ කොයිල් එකිනෙකට ඈතින්
තැබීම වැදගත්.
එහෙත්
හැමවිටම එය කිරීමට අපහසු විය
හැකියි.
තවද,
එක්
කොයිලයක් අනෙක් කොයිලයට ලම්භකව
හෙවත් අංශක90ක
කෝණයකින් තැබීමෙන්ද එය බොහෝදුරට
වැලැක්විය හැකියි.
(මතකද
මා මීට පෙර උපමාවකිනුත් පැහැදිලි
කළා පිරිසක් මැද සිටින විට
ඔවුන්ගේ ඇඟේ නොවදින සේ ඔබට
අත් සෙලවීමට නම් අත් ඉහල පහල
සොලවන්න කියා?
ඒ
කියන්නේ චුම්භක ක්ෂේත්ර
දෙකක් ලම්භකව ඇති විට ඒ දෙක
අතර අන්යොන්ය ක්රියාකාරිත්වය
ඇන හිටිනවා.)
පහත
රූපයේ A
වලින්
දැක්වෙන්නේ කොයිල් දෙකක්
ළඟින් ඇති විට කරදරකාරී
අන්යොන්ය ප්රේරණය ඇති වන
අවස්ථාවක්.
B වලින්
දැක්වෙන්නේ කොයිල් දෙක ඈත්
කළ විට එය අවම වන හැටි.
C වලින්
දැක්වෙන්නේ කොයිල් දෙක ලම්භකව
තැබීමෙන් එය ඉතාම අවම කිරීමයි.
මෙම
විස්තරය අනුව ඔබට වැටහී යා
යුතු දෙය නම්,
අන්යොන්ය
ප්රේරණයේ ප්රමාණය කොයිල්
දෙක තිබෙන දුර හා ඒවා පිහිටුවන
ආකාරය (orientation)
අනුව
වෙනස් වන බවයි.
එක
කොයිලයක පවතින ක්ෂේත්රය
දුබල නම්,
එයින්
අනෙක් කොයිලය මත ඇති කරන බලපෑම
අවම විය හැකි අතර,
අනෙක්
කොයිලය ප්රබල නම්,
එවිට
එම කොයිලයෙන් ඇතිවන බලපෑම
ඉහලය.
ඒ
කියන්නේ කොයිල් දෙකට වෙනස්
අන්යොන්ය ප්රේරණ ප්රමාණයන්
ඇතිවිය හැකියි.
පළමු
කොයිල් එකට දැනෙන අන්යොන්ය
ප්රේරණ ප්රමාණය M1
ලෙසද,
දෙවැනි
කොයිලයට දැනෙන අන්යොන්ය
ප්රේරණ ප්රමාණය M2
ලෙසද
දක්වමු.
මෙම
අගයන් දෙකම වෙනුවට තනි දර්ශීය
අගයක් ගත හැකියි M
ලෙස
මෙම දෙකෙහි ගුණෝත්තර මධ්යන්ය
අගය (එනම්
M1,
M2 එකට
ගුණ කර එහි වර්ගමූල අගය)
ගැනීමෙන්.
කොයිල් දෙක අතර ඇති වන (මධ්යන්ය) අන්යොන්ය ප්රේරණය එම කොයිල් දෙකේ ස්වයං-ප්රේරණතා අගයන් දෙක මඟින්ද දැක්විය හැකියි පහත ආකාරයට.
මෙයි K යනු coefficient of coupling ලෙස හැඳින්වෙන සංගුණකයයි. එහි අගය පෙර සඳහන් කළ පරිදිම කොයිල් දෙක පවතින දුර හා ඒ දෙක එකිනෙකට පිහිටා තිබෙන ආකාරය මත තීරණය වේ. K අගයේ උපරිමය 1 වන අතර අවමය 0 වේ. K = 1 වන විට, ඉන් අදහස් කරන්නේ කොයිල් දෙක ඉතාම හොඳින් "කප්ල්" වී ඇති බවයි (එනම් එක් එක් කොයිලයේ ක්ෂේත්රයන් අනෙක් කොයිලය හොඳින් කපයි). K = 0 වන විට, ඉන් අදහස් කරන්නේ කොයිල් දෙකේ ක්ෂේත්රයන් පොඩ්ඩක්වත් එකිනෙකා කපා නොගන්නා බවයි. පරිපථයක ඉන්ඩක්ටර් ස්ථානගත කරන විට, උත්සහ කළ යුත්තේ මෙම සංගුණකය ශූන්ය කිරීමටයි. (එහෙත් ට්රාන්ස්ෆෝමර්වලදී මීට ප්රතිවිරුද්ධ දේ කළ යුතුය. එනම්, මෙම සංගුණකය 1 බවට පත් කර ගැනීමයි.) ඇත්තටම මෙම සංගුණකය යනු අමුතු දෙයක් නොවේ. ඉහත විස්තරයම ගණිතානුකූලව දැක්වීමට යොදාගත් උපක්රමයක් පමණි.
පරිපථවලදී
ඉන්ඩක්ටිව් කප්ලිං සංසිද්ධිය
හරිම කරදයක් වුවද,
එය
වටිනා කාර්යන් සඳහා ප්රයෝජනයටද
ගත හැකියි.
මේ වෙන
විට වයර්ලස් ක්රමයට විදුලි
ශක්තිය ගමන් කරවීමට මෙම
ඉන්ඩක්ටිව් කප්ලිං ක්රමය
පර්යේෂණය වෙමින් අත්හදා බලමින්
තිබේ.
ෆෝන්,
ප්ලේයර්,
GPS ආදී
උපාංගවලට වයර් සම්බන්ධ නොකර
චාජ් කිරීමේ inductive
charging ලෙස
හැඳින්වෙන ක්රමය මේ වන විටත්
භාවිතයේ පවතී.
එහිදී
ඔබ එම උපාංගය නිකංම මේසය උඩ
(ඉන්ඩක්ටිව්
චාජර් එක ආසන්නයේ)
තැබීම
පමණයි කළ යුත්තේ.
චාජර්
වයර් සම්බන්ධ කිරීමට නැත.
අනාගතයේ ඉලෙක්ට්රික් වාහන චාජ් කිරීමටත් මෙය යොදා ගැනීමට සලකා බලමින් සිටී. එනම්, වාහනය පාකිං කරන විට, ඊට යටින් තබා ඇති මෙවැනි ඉන්ඩක්ටිව් චාජර් එකක් මඟින් වාහනයේ බැටරි චාජ් වේවි.
කිලෝමීටර් දහස් ගණනක් ඉහළ අභ්යවකාශයේ රඳවා තිබෙන යෝධ සූර්ය පැනල මඟින් නිපදවන විදුලිය පොලොවට එවීම ආදී බොහෝ දේවල් මෙම ඉන්ඩක්ටිව් චාජිං ක්රමයෙන් කර ගැනීමට පර්යේෂණ කෙරෙමින් පවතිනවා. ඇත්තටම මෙම ඉන්ඩක්ටිව් කප්ලිං යොදා ගෙන විදුලි ශක්තිය වයර්ලස් ක්රමයෙන් බෙදා හැරීම පිළිබඳ සංකල්පය ඉතා පැරණිය. මෙහි පුරෝගාමියා Nicholas Tesla වේ. තවද, කර්මාන්තවල දැනටත් භාවිතා වන ලෝහ පෑස්සීමට හා යම් යම් දේවල් උණු කිරීමට යොදා ගන්නා inductive heating ක්රමයද ඉන්ඩක්ටිව් කප්ලිං මත පදනම් වේ. ගෙවල්වල භාවිත වන induction cooker යනුද ඉන්ඩක්ටිව් හීටිං ක්රමයකි. දැනටත් බහුලව භාවිතා වෙන RFID (Radio Frequency Identification) ක්රමයද පදනම්ව ඇත්තේ මේ මතයි. මේවා පිළිබඳ පසුවට තව දුරටත් සලකා බලමු.
ප්රේරකයක් පරිපථවලට අවශ්ය කරන්නේ ඇයි? අනිවාර්යෙන්ම ඉහත කතා කළ ඉන්ඩක්ටිව් කප්ලිං සංසිද්ධිය නිසා නම් නොවේ (එය කොයිල්වල වෙනත්ම ප්රයෝජනයකි). තවද, අනොන්ය ප්රේරණය නිසාත් නොවේ (අන්යොන්ය ප්රේරණය භාවිතා කරමින් ට්රාන්ස්ෆෝමර්, මෝටර්, ජෙනරේටර් නිපදවූවත්, ඉලෙක්ට්රොනික්ස් පරිපථ නිර්මාණයට එම ගුණයද වැදගත් නැත). ඒ අනුව, ඉලෙක්ට්රොනික්ස්වලට වැදගත් වන්නේ ස්වයං-ප්රේරණයයි. (ඒ කියන්නේ ඉලෙක්ට්රොනික්ස්වල භාවිතා වෙන්නේ තනි කොයිල්ය.) ඒ ඇයි? පිළිතුර සරලයි.
ස්වයං-ප්රේරණයේදී
(එනම්
කොයිල් එකේ)
ධාරාව
විචලනය වන විට,
එම
විචලනය වැලැක්වීමට නිරායාස
උත්සහයක් ඇති වෙනවනෙ.
මෙන්න
මෙම ගුණය තමයි ප්රයෝජනයට
ගන්නේ.
එය අපට
මෙසේ කිව හැකියි.
"කොයිලයක්/ප්රේරකයක්/ඉන්ඩක්ටරයක්
විදුලි විචලනයට කැමැති නැත;
එය
කැමැති වන්නේ ස්ථාවර ඩීසී
විදුලියකටයි.”
මෙය
බැලූබැල්මට කැපෑසිටර් එකේ
විරුද්ධ ක්රියාව නේද?
කැප්
එකක් නම් කැමැති නැත්තේ ස්ථාවර
ඩීසී විදුලියකටයි;
එය
විචලනය වන විදුලියට ඉතා
කැමැතියි.
එවිට,
ඉන්ඩක්ටරයක්
හරහා ස්ථාවර (විචලනය
නොවන)
ඩීසී
විදුලියක් ගමන් කරන විට,
එම
විදුලියට අමුතුවෙන් බාධාවක්
හෙවත් "ප්රතිරෝධයක්"
එල්ල
කරන්නේ නැත.
එහෙත්
සෑම ඉන්ඩක්ටරයක්ම සෑදී තිබෙන්නේ
සන්නායකයකින් බැවින් සෑම
සන්නායකයකටම ප්රතිරෝධී
අගයක් තිබෙන බැවින්,
අන්න
එම සන්නායකයේ ප්රතිරෝධි අගය
කිසිවිටක ඉවත් කළ නොහැකියි.
එහෙත්
මෙම ප්රතිරෝධි අගය මිලිඕම්
ගණනක් තරම් නොසලකා හැරිය හැකි
තරමේ කුඩා ප්රමාණයකි.
ඇත්තටම
මෙම සන්නායකයේ ප්රතිරෝධය
ඉන්ඩක්ටරයේ ස්ට්රේ රෙසිස්ටන්ස්
එකයි.
අයිඩියල්
(එනම්,
පරිපූර්ණ)
ඉන්ඩක්ටරයක
ඇත්තේ ඉන්ඩක්ටන්ස්/ප්රේරණතාවක්
පමණයි.
මෙතැන්
සිට අයිඩියල් ඉන්ඩක්ටර් ගැන
ඉගෙන ගමු (මීට
පෙරත් අප ඉගෙන ගත්තේ අයිඩියල්
උපාංග ගැන බව ඔබට දැන් මතක්
විය යුතුය).
එහෙත්
ඉහත කියූ ලෙසටම සැබෑ ඉන්ඩක්ටරයක
මීට අමරතව ස්ට්රේ රෙසිසිටන්ස්
එකක් (හා
පසුව පෙන්වා දෙන පරිදි ස්ට්රේ
කැපෑසිටන්ස් එකක්ද)
පවතිනවා.
එහෙත්
මෙහි වැදගත්ම කරුණ නම්,
ස්ථාවර
විදුලියකට අයිඩියල් ඉන්ඩක්ටරයක්
විසින් කිසිම "අමුතුවෙන්"
ප්රතිරෝධයක්
නොදැක්වීමයි.
එහෙත්,
ඉන්ඩක්ටරය
හරහා විචලනය වන විදුලියක්
යවන විට තත්වය වෙනස් වේ.
එනම්,
දැන්
ඉන්ඩක්ටරය විසින් අමුතුවෙන්
ප්රතිරෝධයක් දක්වනවා.
විචලනය
වන වේගය හෙවත් සංඛ්යාතය වැඩි
වන විට,
එම
ප්රතිරෝධකතාව ඉහල යනවා.
ඉන්ඩක්ටරයක්
විසින් ඇති කරන මෙම ප්රතිරෝධයට
"ප්රේරක
ප්රතිභාධකය"
(inductive reactance) යන
නමයි ව්යවහාර කළ යුත්තේ.
මේ
අනුව දැන් අපට ප්රතිබාදක
වර්ග දෙකක් හමු වෙනවා.
මේ දෙක
වෙන් වෙන්ම හැඳින ගැනීමට,
කැප්වල
ඇතිවන ප්රතිබාදකය ධාරිත්රක
ප්රතිබාදකය (Capacitive
Reactance – XC) ලෙසත්
ඉන්ඩක්ටර් නිසා ඇතිවන ප්රතිබාදකය
ප්රේරක ප්රතිබාදකය (Inductive
Reactance – XL) ලෙසත්
නම් කරනවා.
ප්රේරක
ප්රතිබාදකය සොයන සූත්රය
පහත දැක්වේ.
මෙහි
f
යනු
ප්රේරකය හරහා ගලා යන විදුලි
සංඥාවේ සංඛ්යාතය වන අතර,
L යනු
ප්රේරකයේ අගයයි.
කෝණික
සංඛ්යාතය යොදා ගන්නා විට
දෙවැනි සූත්රය ලිවිය හැකියි.
තවද, (අයිඩියල්) ඉන්ඩක්ටරයක ධාරාව හා විභවය අතර අංශක 90ක කලා වෙනසක් පවතී. ධාරාවට වඩා අංශක 90ක් ඉදිරියෙන් විභවය ගමන් කරයි. (මෙයත් කැප් එකේ ක්රියාකාරිත්වයට ප්රතිවිරුද්ධයි නේද? මතකද කැප්වල ධාරාවයි අංශක 90කින් විභවයට වඩා ඉදිරියෙන් ගමන් කළේ.) පහත දැක්වෙන්නේ ධාරා හා විභව සංඥා දෙක පවතින ආකාරයත්, එයම ෆේසර් ඩයග්රෑම් එකක දක්වන ආකාරයත්ය.
මෙම
කාරණය නිසා ධාරිත්රකවල සිදු
කළ විග්රහයම අනුව,
ඉන්ඩක්ටරයක්
යම් ප්රතිරෝධි අගයක් දැක්වුවත්,
එය තාප
උත්සර්ජනයක් නොවේ.
එනිසයි
ප්රතිභාධකය යන වචනය යොදා
ගත්තේ.
ඉලෙක්ට්රෝනික්ස් (electronics) ...
ඉලෙක්ට්රෝනික්ස් (electronics) ...










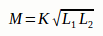





Comments
Post a Comment
Thanks for the comment made on blog.tekcroach.top