ඉහත
විස්තරවලදී පුන පුනා කියපු
දෙයක් තමයි කට්-ඕෆ්
සංඛ්යාතය යනු ප්රතිරෝධකයේ
අගය හා කැප් එකේ ප්රතිභාදක
අගය සමාන වන අවස්ථාව බව.
එවිට
ඉන්පුට් වෝල්ටියතාව හරියටම
දෙකට බෙදී කැප් එක හා රෙසිස්ටරය
දෙපස ඩ්රොප් වෙනවා යනුවෙන්
එහිදී පැවසුවා.
ඒ
කියන්නේ කට්-ඕෆ්
සංඛ්යාතයේදී අවුට්පුට්
වන්නේ ඉන්පුට් වෝල්ටියතාවෙන්
හරි අඩක්ද?
(උපාංග
දෙක වෙන් වෙන්ව සලකන විට එලෙස
සිතෙනවා නේද?)
ජවය
අනිවාර්යෙන්ම අඩකින් අඩු
වෙනවා.
ඒ
අනුව,
ජවය
පදනම් කරගෙන ඩෙසිබල් වලින්
එය -3dB
ලෙස
හෝ වෝල්ටියතාව පදනම් කරගෙන
එයම -6dB
ලෙස
සඳහන් කළා ඔබට මතක ඇති.
එහෙත්
තවත් සැඟවුණු කරුණක් මෙහි
තිබෙනවා.
එනම්,
කැප්
එකේ දෙපස ඩ්රොප්වන වෝල්ටියතාව
හා රෙසිස්ටරය දෙපස ඩ්රොප්වන
වෝල්ටියතාව විෂම කලාවේ පවතින්නේ.
එවිට,
ඉහත
පරිපථය නිවැරදිව හා පහසුවෙන්
නිර්මාණය කිරීම පිණිස R
හා
C
හරහා
ඉන්පුට් වෝල්ටියතාවෙන් අඩක්
බැගින් පිහිටනවා යැයි කිව්වත්,
අර
කලාවේ බලපෑම නිසා සත්ය ලෙසම
එම වෝල්ටියතාවන් වෙනස් වේ.
සත්ය
ලෙසම පිහිටන වෝල්ටියතාවන්
පවා ගණනය කළ හැකියි.
ඒ
සඳහා සරල අංකගණිත ආකලනය වෙනුවට
දෛශික (පෛතගරස්)
ආකලනය
යොදාගත යුතුය.
සරල
අංකගණිත ආකලනය අනුව,
ඉහත
LPF
එකේ
අවුට්පුට් වෝල්ටියතාව සෙවීමට,
ඉහත සූත්රය
අනුව නම්,
කට්-ඕෆ්
සංඛ්යාතයේදී අවුට්පුට්
වන්නේ ඉන්පුට් වෝල්ටියතාවෙන්
හරි අඩක් නේද (Xc
= R නිසා)?
එහෙත්
ඉහත විස්තර කළ පරිදි විෂම
කලාවේ බලපෑම නිසා,
පහත
දැක්වෙන දෛශික ආකලන සූත්රයයි
යොදා ගැනීමට සිදු වන්නේ,
ඉහත
සූත්රයේ හරයෙන් දැක්වෙන්නේ
සම්භාදක අගයයි (Z).
දැන්
කට්-ඕෆ්
සංඛ්යාතයේදී අවුට්පුට්
වන්නේ ඉන්පුට් වෝල්ටියතාවෙන්
කොතරම් පංගුවක්දැයි සොයා
බලන්න.
උදාහරණයක්
ලෙස,
Xc=R=100 ohm ලෙස
ගමු.
මෙම
අගයන් ඉහත සූත්රයට ආදේශ කළ
විට,
0.707VI
ලෙස
ලැබේ.
ඒ
කියන්නේ ඉන්පුට් වෝල්ටියතාවෙන්
70%ක්
අවුට්පුට් වෝල්ටියතාව ලෙස
පිට කරනවා (50%
නොවේ).
නිතරම
සිහිතබා ගන්න කලා වෙනස්කමක්
පවතින විට සරල අංකගණිත එකතු
කිරීම (ආකලනය)
යොදන්න
බැහැ.
ෆිල්ටර්
සර්කිට් යනු ඉතාම සරල RC
සර්කිට්
එකකි.
එහෙත්
එහි ගණනය කිරීම්වලට ඩෙසිබල්
යොදා ගැනීම නිසා හා,
ඒවායේ
පවතින කලා වෙනස්කම් නිසා ගණනය
කිරීම් සම්බන්ධයෙන් යම් යම්
පැටලිලි සහගත තත්වයන් මතු
වෙනවා.
එහෙත්
ඒවා නිවැරදිව අවබෝධ කරගත්
විට ඉතාම සරල බව හැඟේවි.
සමහර අවස්ථාවල හර්ට්ස් වලින් මනින සංඛ්යාතය (f) වෙනුවට, “තත්පරයට රේඩියන්" වලින් මනින සංඛ්යාතය (ω) යොදා ගන්නවා. මෙය "කෝණික සංඛ්යාතය" (angular frequency) හෝ "කෝණික ප්රවේගය" (angular velocity) ලෙසද හැඳින්විය හැකියි. සාමාන්ය සංඛ්යාතය හා කෝණික සංඛ්යාතය අතර පහත ආකාරයේ සරල සම්බන්ධතාවකුයි පවතින්නේ. මෙම සරල සම්බන්ධතාව යොදාගෙන ඔබට දැන් පහසුවෙන් එක් සංඛ්යාතයකින් පවතින අගයක් අනෙක් සංඛ්යාතයට හැරවිය හැකියි.
ω = 2πf
මේ අනුව XC = 1/2πfC යන සූත්රයම XC = 1/ωC යනුවෙන්ද ලිවිය හැකියි. තවද, කට්-ඕෆ් සංඛ්යාතය යනු කැප් එකේ ප්රතිභාධක අගය හා රෙසිස්ටරයේ ප්රතිරෝධ අගය සමාන වන තැනයි. ඒ අනුව, කට්-ඕෆ් සංඛ්යාතය අපට පහසුවෙන් පහත ආකාරයට සොයාගත හැකියි.
R = XC → R = 1/2πfCC → fC = 1/2πRC
ඉහත සූත්රයම කෝණික සංඛ්යාතය යොදාගෙන 2πfC = 1/RC → ω = 1/RC ලෙස ලිවිය හැකියි. විවිධ පොත්වල විවිධ ක්රමවලින් දක්වන නිසයි මා මෙවැනි සුලු සුලු කාරණා පවා මතු කරන්නේ. ඒ සියල්ල ගැන දැන සිටීමෙන් ඔබට රසවත්ව හා පහසුවෙන් ඉලෙක්ට්රොනික්ස් උගත හැකි වේවි බොහෝ පතපොත කියවමින්.
පෙර අවස්ථාවක සඳහන් කළා සරල RC සර්කිට් එකක් ෆිල්ටර් සර්කිට් එකක් ලෙස භාවිතා කරන විට, ඩිකේඩ් 1කට ඩෙසිබල් 20ක හායනයක් සිදුවන බව. ඇත්තටම එම ප්රකාශය වඩා පුලුල් වීම පිණිස මා කැමතියි එය තරමක් මෙසේ වෙනස් කරන්නට. කැපෑසිටර් හා ඉන්ඩක්ටර් යනු ප්රතිභාධක අගයන් පෙන්විය හැකි උපාංග දෙකක් (තවම ඉන්ඩක්ටර් ගැන අප ඉගෙන ගෙන නැත). එවැනි ප්රතිභාධකයන් දැක්විය හැකි උපාංග reactive ලෙස හැඳින් වෙනවා. ඒ අනුව, කැප් හා ඉන්ඩක්ටර් රියැක්ටිව් උපාංග දෙකක් වුවත්, රෙසිස්ටරය රියැක්ටිව් නොවේ. යම් ෆිල්ටර් සර්කිට් එකක රියැක්ටිව් උපාංග (එනම්, කැප් හෝ ඉන්ඩක්ටර්) ඇත්තේ එකක් පමණක් නම්, එවැනි ෆිල්ටර් එකක හායනය -20dB/decade වේ. මේ අනුව මෙතෙක් අප සලකා බැලූ HPF හා LPF යන දෙකම -20dB/decade හායනයක් සහිත ෆිල්ටර් වේ. අප ඒ හැම අවස්ථාවකම භාවිතා කළේ එක කැප් එකක් පමණි. මෙවැනි එක් රියැක්ටිව් උපාංගයක් යොදාගෙන සාදනු ලබන ෆිල්ටර් first-order filter (1st order filter) හෝ single-pole filter ලෙස හැඳින්වෙනවා. ඒ කියන්නේ, මෙවැනි රියැක්ටිව් උපාංග දෙකක් යොදාගෙන second-order filter (2nd order filter) හෙවත් two-pole filterද සෑදිය හැකියි. එවිට, ෆිල්ටර් එකේ හායනය තවත් වැඩි වේ (එනම්, ස්ලොප් එක/රෝල්-ඕෆ් එක වැඩි වේ). එනම්, හායනය දෙගුණ වේ (-40dB/decade). මෙලෙස ෆිල්ටර් කොටස් තව තවත් එකතු කර third-order, fourth-order ආදී ෆිල්ටර් සෑදිය හැකියි. ඒ සෑම ෆිල්ටර් කොටසකම -20dB/decade හායනය බැගින් එකතු වේ. මෙලෙස ෆිල්ටර් කොටස් එකතු කළ හැකි ආකාර කිහිපයක් පැවතිය හැකියි. පහත දැක්වෙන්නේ එවැනි සරල සම්බන්ධතාවකි.
ඉහත කර තිබෙන්නේ පළමු ෆිල්ටර් කොටසේ අවුට්පුට් එක දෙවැනි ෆිල්ටර් කොටසට ඇතුලු කිරීම නේද? බැලූබැල්මට මෙවැනි කොටස් රාශියක් එකතු එකතු කර, ෆිල්ටර් එකේ බෑවුම වැඩි කරගෙන ඉස්තරම්ම ෆිල්ටර් එකක් සාදාගත හැකි යැයි සිතුනත්, මෙවැනි සරල ෆිල්ටර්වලට වඩා උසස් තත්වයේ ෆිල්ටර් වෙනත් ක්රමවලින් සාදාගත හැකියි. මෙවැනි ෆිල්ටර්වල හැමවිටම ඉන්පුට් සංඥාවට වඩා අවුට්පුට් සංඥාව කුඩාය; එනම්, වැලැක්විය නොහැකි අනිවාර්ය හායනයක් පවතී. මෙවැනි සරල RC (හා RL හා RCL) ෆිල්ටර් එමනිසා passive filter ලෙස හැඳින්වෙනවා (කිසිදු ඇක්ටිව් උපාංගයක් ෆිල්ටර් තුළ නැති නිසාද පැසිව් යන නම යෙදේ; ඇක්ටිව් හා පැසිව් උපාංග ගැන මොහොතකින් පැහැදිලි කෙරේ). සාමාන්යයෙන් ඉහත වැනි ෆස්ට් ඔ්ර්ඩර් පැසිව් ෆිල්ටර් එහි ඇති සරලකම හා පහසුව නිසාම බහුලව භාවිතා වෙනවා. සෙකන්ඩ් ඕර්ඩර් පැසිව් ෆිල්ටර්ද භාවිතා වෙනවා. සර්කිට් ලෝඩිං වීම ෆිල්ටර් කොටස් කිහිපයක් එකතු කර සාදන පැසිව් ෆිල්ටර්වල ඇති ප්රධානතම ගැටලුවයි. එය වැලැක්විය හැකියි පසු ෆිල්ටර් කොටස්වල ප්රතිරෝධකය ඊට පෙර කොටසේ ප්රතිරෝධකය මෙන් අඩුම ගාණේ දසගුණයක් වැඩි අගයක් යෙදීමෙන්. (මෙය නේද සර්කිට් ලෝඩිං වැලැක්වීමට හැමවිටම යොදාගන්නා කෝකටත් තෛලය?) එනම්, R2 = 10R1, C2 = 10C1, R3 = 10R2, C3 = 10C2 ආදී ලෙස. එහෙත් ප්රායෝගිකව එසේ ප්රතිරෝධ අගයන් දසගුණ කරමින් කොටස් ගණනාවක් එකතු කිරීමේ බාධා ඇත.
ට්රාන්සිස්ටර් හා අයිසී උපයෝගී කරගෙන සංඥාව වර්ධනය කරන ෆිල්ටර් නිපදවිය හැකියි. එවිට, ඉහත සර්කිට් ලෝඩිං ගැටලුව පහසුවෙන්ම අවම කළද හැකියි. ඒවා ගුණාත්මකබවින්ද ඉහළයි. මෙවැනි ෆිල්ටර් active filter ලෙස හැඳින්වෙනවා. ඉහල ඕර්ඩර්වල (higher order) පැසිව් ෆිල්ටර්වලට වඩා ඇක්ටිව් ෆිල්ටර් කොලිටියෙන් වැඩිය.
ඉහත රූපයේ පෙනෙන සෙකන්ඩ් ඕර්ඩර් පැසිව් ෆිල්ටර් එක තරමක් විශ්ලේෂණය කරමු. කට්-ඕෆ් සංඛ්යාතයේදී පළමු RC කොටසින් අවුට්පුට් වන වෝල්ටියතාව වන්නේ ඉන්පුට් වෝල්ටියතාවෙන් 70.7% කි. දැන් දෙවන කොටසේ ෆිල්ටර් එකද ඊට ලැබෙන වෝල්ටියතාවෙන් 70.7% ක් තමයි නැවත එලියට ලබා දෙන්නේ. එය මුල් ෆිල්ටර් කොටසට ලබා දුන් ඉන්පුට් වෝල්ටියතාවට සාපේක්ෂව, 70.7% x 70.7% (හෙවත් 0.707 x 0.707 = 0.499) කි. එය සුලු කළ විට, 49.9% (ආසන්න අගයට ගත් විට, 50%) කි. මේ ආදී ලෙස ඔබට හැකියි තව තවත් ෆිල්ටර් කොටස් එකතු කරන විට, ඒ සියල්ලම විසින් කට්-ඕෆ් සංඛ්යාතයේදී ඉන්පුට් වෝල්ටියතාවෙන් කොපමණ ප්රතිශතයක් පිට කරනවාදැයි ගණනය කිරීමට. එය සූත්රයක් ලෙස (0.707)n ලෙස ලිවිය හැකියි (n යනු ෆිල්ටර් කොටස් ගණනයි). මේ අනුව RC ෆිල්ටර් කොටස් 3ක් සහිත ෆිල්ටරයකින් (0.707)3 = 70.7% x 70.7% x 70.7% = 35% කි.
වෙනස් වෙනස් RC ෆිල්ටර් සර්කිට් දෙකක් හෝ කිහිපයක් ඉහත රූපයේ ආකාරයට සම්බන්ධ කළ හැකියි. එවිට, අප සිතන්නට පෙළඹෙන්නේ මෙසේය. පළමු ෆිල්ටර් කොටසේ ඇති R හා C වල අගයන් මත සුපුරුදු පරිදි කට්-ඕෆ් සංඛ්යාතය හා අනෙකුත් ෆිල්ටර් සාධක තීරණය වන බවත්, එසේ ෆිල්ටර් වෙච්ච සංඥාව තමයි දැන් දෙවැනි ෆිල්ටර් කොටසට අැතුලු වෙන්නේ. දැන් මෙම දෙවැනි ෆිල්ටර් එක වෙනමම සලකා බලනවා. ඒ කියන්නේ දෙවැනි ෆිල්ටර් කොටසේ පවතින R හා C අගයන් මත කට්-ඕෆ් සංඛ්යාතය ආදිය නැවත තීරණය වෙනවා. මේ ආදි ලෙස ඉදිරියට ඇති අනෙක් ෆිල්ටර් කොටස් ගැනද වෙන වෙනම සිතනවා. මෙලෙස සිතීමෙන් කිසිම ප්රශ්නයක් නැහැ මේ සෑම ෆිල්ටර් කොටසකම පවතින කැප්වල අගයන් හා රෙසිස්ටර්වල අගයන් එක සමානයි නම්. එහෙත් සිතන්න පළමු ෆිල්ටර් කොටසේ R හා C අගයන්ට වඩා දෙවැනි ෆිල්ටර් කොටසේ R හා C අගයන් වෙනස් වූවොත් කුමක් සිදු වේවිද? (ඉහත සර්කිට් ලෝඩිං ප්රශ්නය නැති කිරීමට එසේ කරන්නට සිදු වෙනවානේ.) එවිට, පළමු කොටසින් යම් කට්-ඕෆ් සංඛ්යාතයක් සහිතව ෆිල්ටර් වෙච්ච සංඥාව දෙවැනි කොටසට ඇතුලු වී එම දෙවැනි කොටසේදී වෙනත් කට්-ඕෆ් සංඛ්යාතයක් සහිතව ෆිල්ටර් වේ. ඒ කියන්නේ R, C අගයන් වෙනස් වන විට, එක් එක් කොටසේ කට්-ඕෆ් සංඛ්යාත වෙනස් වේ. මේ ආදී ලෙස එක් එක් ෆිල්ටර් කොටසේ කට්-ඕෆ් සංඛ්යාතයන් වෙන වෙනම ගණනය කර, අවසානයේ මේ සියල්ලෙහිම "සමක කට්-ඕෆ්" අගය සෙවිය යුතුය. එම සමක කට්-ඕෆ් සංඛ්යාතය තමයි සම්පූර්ණ ෆිල්ටරයේ කට්-ඕෆ් සංඛ්යාතය ලෙස සලකන්නේ. මෙලෙස එක එක කොටසින් කට්-ඕෆ් සංඛ්යාතයන් වෙනස් වීම ගැන තක්සේරු කිරීම කරදරකාරී වේ. අපට පුලුවන් පහත දැක්වෙන සරල සූත්රයෙන් කොටස් දෙකකින් යුත් සම්පූර්ණ ෆිල්ටර් එකේම කට්-ඕෆ් සංඛ්යාතය සොයා ගන්නට.
ඉහත සූත්රය ෆස්ට් ඕර්ඩර් RC ෆිල්ටර් එකේ කට්-ඕෆ් සංඛ්යාතය සොයන සූත්රය සමග සංසන්දනය කරන්න. දෙකම එකිනෙකට අනුරූප බව පෙනේවි. මෙහිදී ඇත්තටම වී තිබෙන්නේ ෆිල්ටර් කොටස් දෙකේ තිබෙන R1, R2 රෙසිස්ටර් අගයන් දෙක එකට ගුණ කර එහි වර්ගමූලයද, C1, C2 කැප් අගයන් දෙක එකට ගුණ කර එහි වර්ගමූලයද ගැනීමයි. එනම්, විවිධ අගයන් ඇති විට, ඒවායේ යම් "පොදු තනි අගයක්" බවට ඒවා පත් කරගනී. (යම් අගයන් දෙකක් ගුණ කර ඉන්පසු එහි වර්ගමූලය ගැනීම ගණිතයේදී මධ්යනය අගය සොයන එක් ක්රමයක්.) ඉන්පසුව එම මධ්යන්ය අගයන් දෙක සාමාන්ය ෆස්ට් ඕර්ඩර් සූත්රයේ R හා C වලට ආදේශ කළ හැකියි.
ෆිල්ටර් කොටස් තුනක් හෝ වැඩි ගණනක් පවතින අවස්ථාවද මේ ලෙසම තර්ක කර බලන්න. කොටස් තුනක් ඇති අවස්ථාව බලමු. මෙහිදී ප්රතිරෝධක අගයන් තුන එකට ගුණ කර, තුන්වෙනි මූලයද, ධාරිත්රක තුනේ අගයන් එකට ගුණ කර, තුන්වෙනි මූලයද ගත යුතුය. මේ ආදී ලෙස ගත යුතු මූලය ඕර්ඩර් එකට සමාන වේ. ඕනෑම ඕර්ඩර් එකක් සඳහා පහත ආකාරයට පොදු සූත්රයක් ලිවිය හැකියි. ප්රතිරෝධක n ගණනක් ඇති විට, ඒ සියලු ප්රතිරෝධක අගයන් එකට ගුණ කර ලැබෙන පිළිතුරෙහි n වැනි මූලය සොයන්න. එලෙසම කැප්වලටත් කරන්න. ඉන්පසු එම අගයන් සාමාන්ය කට්-ඕෆ් සංඛ්යාතය සොයන සූත්රයට ආදේශ කරන්න. මෙම සූත්රය ගැන කල්පනා කළ යුත්තේ අන්න ඒ ලෙසටයි. අමුතුවෙන් පාඩම් කරන්නට දෙයක් මෙහි නැත.
කොටස් දෙකක් සම්බන්ධ කර සාදන සෙකන්ඩ් ඕර්ඩර් පැසිව් ෆිල්ටර් එකක ෆිල්ටර් වීම පෙන්වන ප්රස්ථාරයක් පහත රූපයේ දැක්වේ. නිල්පාට වක්රයෙන් පෙන්වන්නේ පළමු කොටස පමණක් තිබෙන විට ෆිල්ටරයේ බෑවුමයි. දම්පාටින් පෙන්වන්නේ කොටස් දෙකම තිබෙන විට ෆිල්ටරයේ බෑවුමයි. තවද, ෆිල්ටර් කොටස් දෙකේ යෙදෙන R හා C අගයන් වෙනස් වීම නිසා, කට්-ඕෆ් සංඛ්යාතයට එය බලපා ඇති අයුරුත් මෙහි පේනවා. එනම්, කට්-ඕෆ් සංඛ්යාතය තරමක් වෙනස් වී (පස්සට ගොස්) ඇත.
ඉහත LPF සඳහා සෙකන්ඩ් ඕර්ඩර් පැසිව් RC ෆිල්ටර් සර්කිට් නිර්මාණය කරන ආකාරයටමයි HPF වල ඉහල ඕර්ඩර් ෆිල්ටර් සාදන්නේ. සූත්රද වෙනස් නොවේ. එවැනි HPF සෙකන්ඩ් ඕර්ඩර් ෆිල්ටර් පරිපථයක් පහත දැක්වේ.
ඉහත HPF හා LPF ෆිල්ටර් දෙකක් එකට කනෙක්ට් කිරීමෙන් බෑන්ඩ්පාස් ෆිල්ටර් සෑදීමට හැකියි (පහත රූපය). දැන් බලමු බෑන්ඩ්පාස් ෆිල්ටර් එකක් එලෙස සාදා ගන්නා අයුරු. කට්-ඕෆ් සංඛ්යාත දෙක පළමුව තීරණය කළ යුතුයි. ඉන් අපර් කට්-ඕෆ් සංඛ්යාතය තමන්ගේ කට්-ඕෆ් සංඛ්යාතය ලෙස යොදා ගත් ලෝපාස් ෆිල්ටර් එකක්ද, ලෝවර් කට්-ඕෆ් සංඛ්යාතය තමන්ගේ කට්-ඕෆ් සංඛ්යාතය ලෙස යොදා ගත් හයිපාස් ෆිල්ටර් එකක්ද ශ්රේණිගතව සම්බන්ධ කරන්න.
එවිට, අවශ්ය සංඛ්යාත පරාසය පමණක් ගමන් කරවනවා එම පරාසයට පිටින් තිබෙන සංඛ්යාත ෆිල්ටර් කරමින්. පැහැදිලිවම බෑන්ඩ්පාස් ෆිල්ටර් එකක් යනු ස්වභාවයෙන්ම සෙකන්ඩ් ඕර්ඩර් ෆිල්ටරයකි මොකද එම ෆිල්ටරයේ රියැක්ටිව් උපාංග (කැප්) දෙකක් යොදාගෙන තිබෙනවා. බෑන්ඩ්පාස් ෆිල්ටරයක බෝඩ් ප්ලොට් එක පහත දැක්වේ.
උදාහරණයක් ගෙන බලමු. හර්ට්ස් 20ත් කිලෝහර්ට්ස් 20ත් අතර සංඛ්යාත පමණක් යෑමට සලස්වන බෑන්ඩ්පාස් ෆිල්ටරයක් සාදමු. මෙහිදී ෆිල්ටරය කොටස් දෙකක් ලෙස සලකා සැලසුම් කළ යුතුයි. එකක් නම් හර්ට්ස් 20ට අඩු සංඛ්යාත ෆිල්ටර් කර දමන HPF එකක් වන අතර, අනෙක හර්ට්ස් 20,000ට වැඩි සංඛ්යාත ෆිල්ටර් කර දමන LPF කි. මේ දෙක පෙර ඔබ උගත් පරිදි ගණනය කරන්න.
ඉහත බෑන්ඩ්පාස් ෆිල්ටර් සර්කිට් එකේ C1, R1 දෙක එක්ව සාදන්නේ HPF ක් කියා බැලූ බැල්මට පෙනේ. එහි කට්-ඕෆ් සංඛ්යාතය 20 වේ. ඔබ දන්නවා දැන් ෆිල්ටරයේ ප්රතිරෝධක/සම්භාදක අගය සොයන්නේ මෙම ෆිල්ටරය කනෙක්ට් කරන අනෙක් පරිපථ කොටස් අනුව බව. උපකල්පනය කරමු R1 = 1000 ohm හා R2 = 10000 ohm ලෙස තිබිය යුතුයි කියා. ඒ අනුව, කැප් එකේ අගය ගණනය කරන්න. එලෙසම C2, R2 එක්ව සාදන්නේ LPF යි. මෙහි කට්-ඕෆ් සංඛ්යාතය වන්නේ හර්ට්ස් 20,000 වේ. එහිදිත් කැප් එකේ අගය ඔබට ගණනය කරන්න පුලුවන්නෙ. ඔබට C1= 8u හා C2= 0.8n ලෙස ලැබෙනවාද බලන්න ඔබේ ගණනය කිරීම් මඟින්?
ඇත්තටම ඉහත බෑන්ඩ්පාස් ෆිල්ටරය ගුණාත්මකබවින් නම් එතරම් ඉහල නැත. පසුවට ඉගැන්වෙන ක්රම යොදාගෙන ඉස්තරම් වර්ගයේ (ඇක්ටිව්) ෆිල්ටර් වර්ග සාදා ගත හැකියි. මෙවැනි බෑන්ඩ්පාස් ෆිල්ටර් කිහිපයක් එකට එකතු කර (ඕර්ඩර් එක ඉහල දැමීමෙන්) බෑවුම වැඩි කරගත හැකියි.
ඉහත ලෝපාස්, හයිපාස්, බෑන්ඩ්පාස් ආදි ලෙස නම් කෙරුණු ෆිල්ටර්ම විවිධ අවස්ථාවල යෙදෙන අතර, සමහර වෙලාවට ඒ ඒ අවස්ථාවේ නමින්ද එම ෆිල්ටර් හැඳින්වෙනවා. hiss filter, pop filter, treble-cut filter, bass-cut filter, hum filter ආදී ලෙස ඔබට මේවා දැක ගත හැකියි. උදාහරණයක් ලෙස, ට්රෙබල් කට් ෆිල්ටර් එකක් යනු ලෝපාස් ෆිල්ටරයකි. එම ෆිල්ටරයෙන් සිදු කෙරෙන්නේ ශබ්දයක අධිසංඛ්යායන් ඉවත් කිරීමයි (ශබ්දයක අධිසංඛ්යාතයන් treble යනුවෙන් හැඳින්වෙනවා). එලෙසම ශබ්දයක බේස් (bass යනු ශබ්දයක අවසංඛ්යාතයන්ය) කැපීමට යොදාගන්නා බේස් කට් ෆිල්ටරය හයිපාස් ෆිල්ටරයකි.
ඔබේ නිවසට ලැබෙන ප්රධාන විදුලිය (mains electricity) හර්ට්ස් 50ක සංඛ්යාතයක් සහිත ඒසී විදුලියකි (ඇමෙරිකාව වැනි සමහර රටවල එය හර්ට්ස් 60 වේ). හර්ට්ස් 50ක සංඥාවක් යනු කනට ඇසෙන "ශ්රව්ය පරාසයේ" (20Hz – 20kHz) පවතින්නකි. එය බේස් ශබ්දයකි; ඝෝෂාකාරියි (ඇත්තටම ඔබ හර්ට්ස් 50 හා 60 ඝෝෂාවක් අසන්න එම ඝෝෂාව කෙබදුද කියා වටහගැනීමට; CoolEdit/Audition වැනි පරිගණක සොෆ්ට්වෙයාර් එකකින් ඕනෑම සංඛ්යාතයක ශබ්දයක් ඔබට නිර්මාණය කළ හැකියි). ඉතිං සමහර අවස්ථාවල විවිධ ක්රම මඟින් මෙම ප්රධාන විදුලි සංඛ්යාතය සර්කිට් එක හරහා යන සංඥාව හා මුසු වේ. ඒ විතරක් නොවේ මෙම සංඛ්යාතයේ දෙගුණය (හර්ට්ස් 100 හෝ 120) ද එලෙසම කරදරකාරි ලෙස මුසු වේ. මෙන්න මෙවැනි ප්රධාන විදුලිය නිසා ඇති වන හර්ට්ස් 50/100 (හෝ 60/120) ඝෝෂාව හඳුන්වන්නේ "හම්" (hum) එක කියාය. මෙම ඝෝෂාව කනට ඇසෙන්නේ "හ්ම්ම්ම්ම්" ලෙස නිසයි මෙම නම ඊට ලැබී ඇත්තේ. මෙම හම් ඝෝෂාව ෆිල්ටර් කිරීමට යොදන හම් ෆිල්ටරය යනු බෑන්ඩ්ස්ටොප් ෆිල්ටරයකි (එනම්, හර්ට්ස් 50/100 හෝ 60/120 සංඛ්යාත පමණක් ෆිල්ටර් කරයි).
සටහන
කනට ඇසෙන්නේ හර්ට්ස් 20ත් 20,000ත් අතර සංඛ්යාතයන්ගෙන් යුතු ශබ්ද පමණක් බව ඔබ දැන් දන්නවා. හර්ට්ස් 20ට අඩු ශබ්ද infrasound (අධෝධ්වනි) ලෙසද, හර්ට්ස් 20000ට වැඩි ශබ්ද ultrasound (අතිධ්වනි) ලෙසද හැඳින්වෙනවා. ඇත්තටම සෑම මනුස්සයෙකුටම මෙම සම්පූර්ණ පරාසය තුළ සියලු ශබ්ද ඇසෙන්නේ නැත. ක්රමයෙන් වයසට යන විට, ක්රමයෙන් මෙම පරාසය පටු වෙනවා. (ඒ කියන්නේ උඩ හා යට සීමාවන් එකිනෙකට ළං වෙනවා. උදාහරණයක් ලෙස, වයස 65 පමණ වන විට සමහරවිට හර්ට්ස් 40ත් 18000ත් අතර පරාසය දක්වා පටු විය හැකියි). එහෙත් සමහර සතුන්ට ඉහත සංඛ්යාතවලින් පිටත ශබ්ද පවා ඇසිය හැකියි (වවුලන්, තල්මසුන්, බල්ලන් වැනි සතුන්ට).
විද්යාවේදී "ශබ්දයේ සංඛ්යාතය" යන වචනය භාවිතා කළත්, සංගීතයේදී හා ශබ්ද විද්යාවේදී (acoustics) මීට pitch (තාරතාව) කියාද පවසනවා. මෙම ශ්රව්ය පරාසය තුළ ඉහළ පිච් (high pitch) ශබ්ද හැඳින්වෙන්නේ treble (උච්ච ස්වරය) ලෙස වන අතර, පහල පිච් (low pitch) ශබ්ද හැඳින්වෙන්නේ bass (මන්ද්ර ස්වරය) ලෙසයි. ට්රෙබල් හා බේස් ශබ්දවලට හරියටම අහවල් අහවල් සංඛ්යාත පරාස තිබේ යැයි සම්මතයක් නැත. දළ වශයෙන් බේස් යනු හර්ට්ස් 200ට අඩු සංඛ්යාත (එනම්, හර්ට්ස් 20ත් 200ත් අතර) ලෙසද, ට්රෙබල් යනු හර්ට්ස් 4000ට වැඩි සංඛ්යාත (එනම්, හර්ට්ස් 4000ත් 20000ත් අතර) ලෙසද මතක තබා ගන්න. එවිට, හර්ට්ස් 200ත් 4000ත් අතර සංඛ්යාත කලාපයටද midrange ලෙස නමක් ලබා දේ.
සාමාන්යයෙන් හොඳ සවුන්ඩ් සිස්ටම් එකක ස්පීකර් ගණනාවක් පවතින්නේ ඉහත හේතුව නිසාමයි. එක් ස්පීකරයකින් ඉතා හොඳ ගුණාත්මක බවින් යුතු ශබ්දයක් ඇති කළ නොහැකියි සම්පූර්ණ ශ්රව්ය සංඛ්යාත පරාසය පුරාම. එනිසා ප්රධාන ලෙස ස්පීකර් වර්ග 3ක් නිපදනවා. ඉන් එකක් tweeter කියා හැඳින්වෙනවා. මෙම ස්පීකර් අනෙක් ඒවාට වඩා කුඩාය. ට්රෙබල් ශබ්ද ඉතා හොඳින් මෙම ට්වීටර් හරහා පිට කළ හැකියි. මෙම ස්පීකර්වලට බේස් හෝ මිඩ්රේන්ජ් ශබ්ද යවන්න නරකයි. එලෙසම woofer ලෙසද ස්පීකර් වර්ගයක් තිබෙනවා. මෙම ස්පීකර් අනෙක් ඒවාට වඩා විශාලයි. බේස් ශබ්ද සඳහායි වූෆර් සාදා තිබෙන්නේ. මිඩ්රේන්ජ් සංඛ්යාත ශබ්ද සඳහා සාමාන්ය ප්රමාණයේ midrange ස්පීකර් නිපදවා තිබෙනවා. මේ එක් එක් ස්පීකරය සඳහා ඊට සුදුසු සංඛ්යාත පරාසයන් පමණක් යොමු කළ යුතු වෙනවා. එය සිදු කරන්නේද ෆිල්ටර් හරහාය. සාමාන්ය ශබ්දය ලෝපාස් ෆිල්ටරයක්, හයිපාස් ෆිල්ටරයක්, බෑන්ඩ්පාස් ෆිල්ටරයක් යන තුන් වර්ගයේම "ෆිල්ටර් සෙට් එකක්" හරහා යවනවා. එහිදී ඒ ඒ ෆිල්ටර්වලින් පිටවන තරංග ඉහත ස්පීකර් වර්ග තුනට වෙන වෙනම ලබා දෙනවා. ඇත්තටම ඉහත "ෆිල්ටර් සෙට් එක" crossover network ලෙසයි හැඳින්වෙන්නේ.
ඒ විතරක් නොවේ, එම ඇසෙන සංඛ්යාත පරාසය තුළ සෑම ශබ්දයක්ම එකම ආකාරයට දැනෙන්නේද නැත. සාමාන්යයෙන් සංඛ්යාතය ඉහළට යන විට ශබ්දයේ සැර වැඩියෙන් දැනේ. මෙහෙම සිතන්න. සිතමු වොට් 1ක ජවයක් ඇති හර්ට්ස් 100ක ශබ්දයකුයි වොට් 1ක ජවයක් ඇති හර්ට්ස් 10000ක ශබ්දයකුයි ඔබට ඇසෙනවා කියා. දෙකේම ජවය (ශක්තිය) සමානයි. එහෙත් ඔබේ කනට දැනෙන්නේ හර්ට්ස් 10000 ශබ්දය ඉතා වැඩි ශබ්දයක් සහිත ලෙසයි. ඇත්ත වශයෙන්ම ශබ්ද දෙකේම ශක්තිය සමානයි. එහෙත් මෙතැන සිදු වී ඇත්තේ ඉහළට යන සංඛ්යාතයන්ට කන ක්රමයෙන් සංවේදී වැඩි වීමයි. මෙන්න මෙම මූලික ප්රශ්නය නිසා තමයි සංගීතයේදී සවුන්ඩ් මික්සිං කරන්නට සිදුවන්නේ. උදාහරණයක් ලෙස, ඉහල සංඛ්යාතයක් සහිත සංගීත භාණ්ඩයේ හඬ පහල සංඛ්යාතයක් සහිත සංගීත භාණ්ඩයේ හඬට වඩා කැපී පෙනේ. එවිට රසය අඩු වේ. එමනිසා sound mixing මඟින් මේවා ගාණට "බැලන්ස්" කළ යුතුයි.
සංගීත නිර්මාණයේදී ලොකු ස්ටූඩියෝ ඇතුලේ බරපතල කාර්යක් ලෙස ඉහත සවුන්ඩ් මික්සිං සිදු කරනවා. ඔබද මෙම දේම එක්තරා විදියකට සිදු කරනවා ඔබේ ප්ලේයර් එකෙන්. බේස් කොන්ට්රෝල්, ට්රෙබල් කොන්ට්රෝල්, ඊක්වලයිසර් ආදීය තිබෙන්නේ මේ සඳහාය. ට්රෙබල් කන්ට්රෝලර් එක කරකවා ට්රෙබල් ශබ්ද අඩු වැඩි කළ හැකියි. එලෙසම බේස් කන්ට්රෝලර් එක කරකවා බේස් ශබ්ද අඩු වැඩි කළ හැකියි. ඊක්වලයිසර් එකේ විවිධ ස්ලයිඩර්/නොබ් කරකවා සංඛ්යාත පරාසයකම ශබ්දවල සැර වෙන් වෙන්ව වෙනස් කළ හැකියි. ඊක්වලයිසර් එකක් යනු ශ්රව්ය සංඛ්යාත පරාසය තුල යම් ක්රමවත් ක්රමයකට තෝරාගත් සංඛ්යාත හත අටක පමණ ශබ්දයේ සැර/හඬ අඩු වැඩි කළ හැකි පරිදි සෑදූ ෆිල්ටර් සමූහයකි. ඔව්, ඊක්වලයිසර් එකක් යනු ෆිල්ටර් සෙට් (a set of filters) එකක්.
සටහන
විදුලි සංඥා ගැන කතා කරන හැමවිටම වාගේ (විශේෂයෙන් ෆිල්ටර් ගැන කතා කිරීමේදී) සංඛ්යාතය ගැනද කතා කෙරෙනවා. යම් සංඛ්යාතයක දෙගුණය, තුන්ගුණය, දසගුණය ආදී ලෙස "ගුණාකාරයන්" (multiples) ගැනද අපට කතා කළ හැකියි. උදාහරණයක් ලෙස, හර්ට්ස් 100 ගනිමු. එහි දෙගුණය හර්ට්ස් 200 වේ; තුන්ගුණය 300ද, දොලොස්ගුණය 1200ද වේ. පොදුවේ "ගුණාකාරය" (multiple) යන වචනය භාවිතා කළද, විද්යා හා තාක්ෂණයේදී "උපරිතාන" (overtone) යන නම ඊට භාවිතා කෙරේ. ඒ අනුව, හර්ට්ස් 200 හි පළමු උපරිතානය 400ද, දෙවැනි උපරිතානය 600ද වේ. සලකා බලනු ලබන මුල් සංඛ්යාතය "මූලික සංඛ්යාතය" (fundamental frequency) ලෙස හැඳින්වෙනවා.
ඇයි උපරිතාන ගැන අප උනන්දු විය යුත්තේ? ඊට වැදගත් හේතුවක් තිබේ. සමහර පරිපථවල නිතර සිදුවන දෙයක් තමයි යම් විදුලි සංඥාවක සංඛ්යාතයේ විවිධ උපරිතාන ඉබේම නිපැදවීම. එය ඇත්තටම ගැටලුවක්. ඒ කියන්නේ හර්ට්ස් 1000ක සංඥාවක් ගමන් කරන විට, ඒ සමගම හර්ට්ස් 2000, 3000, ආදී සංඥා ඇති වේ. හැමවිටම මෙලෙස සෑදෙන උපරිතාන මූලික සංඛ්යාතය සහිත සංඥාවට වඩා බොහෝ දුර්වලයි (එනම් උපරිතාන සංඥාවල ජවය, ධාරාව, හා වෝල්ටියතාව ඉතාම අඩුයි). උදාහරණයක් ලෙස, වෝල්ට් 1ක සංඥාවේ උපරිතාන සංඥාවක වෝල්ට් ගණන මිලිවෝල්ට් 1ක් පමණ විය හැකියි. ඔබ ඉහතදී දුටුවා ප්රධාන විදුලිය නිසා ඇති වන හම් එක ගැන විස්තරය. එහි විදුලි සංඛ්යාතයට අමතරව පළමු උපරිතානයද ඇතිවන බව දැන් වටහගන්න.
දැනට ෆිල්ටර් ගැන හොඳටම ප්රමාණවත්. දැන් බලමු කැපෑසිටරයක් හා රෙසිස්ටරයක් උපයෝගී කරගෙන සරල delay circuit එකක් සාදාගන්නා අයුරු. ඩිලේ සර්කිට් එකක් යනු විදුලිය සපයපු මොහොතේම ක්රියාත්මක නොවී, විදුලිය සපයා යම් සුලු මොහොතකට පසුව ක්රියාත්මක වන පරිදි සර්කිට් එකකි. මෙහිදී පරිපථය සාමාන්යයෙන් විචලනය නොවන ඩීසී විදුලියකටයි සම්බන්ධ කරන්නේ. එය සෑදීම ඉතාම පහසුයි (පහත රූපය).
මෙහි උපයෝගි කරගෙන තිබෙන්නේ කැපෑසිටර් චාජ් වීමේ ක්රියාවයි. ඔබ දන්නවා කැප් එකක් චාජ් වන වේගය තීරණය කරන්නේ එහි කැපෑසිටන්ස් එක හා ඊට ශ්රේණිගතව සම්බන්ධ කර තිබෙන රෙසිස්ටරයේ (හෝ ප්රතිරෝධයක් දැක්විය හැකි ඕනෑම "කොටසක") ප්රතිරෝධි අගය මතයි. T = RC යන කාල නියතය ගැන මතක් කර ගන්න. ඉහත රූපයේ IN කොටසට විචලනය නොවන විදුලියක් ලබා දෙන විට, එම විදුලිය ධාරිත්රකයට "උරා ගන්නවා" (එනම් ධාරිත්රකය දෙපස ඩ්රොප් වෙනවා). කැප් එක ක්රමයෙන් චාජ් වෙනවා. එවිට එය දෙපස ඩ්රොප් වන විභවයද ක්රමයෙන් ඉහල යනවා (එය ඉහල යන්නේ ධාරිත්රකයේ සුපුරුදු ඝාතීය ශ්රිතයේ ස්වරූපයෙන්). OUT යන කොටසට සම්බන්ධිත උපකරණය ක්රියාත්මක වීමට යම් නිශ්චිත අවම වෝල්ටියතාවක් අවශ්යයි. ඉතිං ධාරිත්රකයේ දෙපස ඩ්රොප් වන විභවයනෙ එම උපකරණයට ලබා ගන්නේ (අවුට්පුට් කරන්නේ). IN කොටසට විදුලිය ලබා දුන් පළමු අවස්ථාවේදී ධාරිත්රකයේ විභවය ශූන්යයි. එහෙත් එය ක්රමයෙන් චාජ් වෙනවා (ඝාතීය ලෙස). එලෙස චාජ් වෙමින්, ධාරිත්රකය දෙපස ඉහත උපකරණයට අවශ්ය අවම වෝල්ටියතාව ඩ්රොප්වන විටම, එම උපකරණය ක්රියාත්මක වෙනවා. තවදුරටත් කැප් එක සමහරවිට චාජ් වේවි. එවිට, විභවය තව තවත් ඉහල යාවි. එනිසා සවි කරන උපකරණය කැප් එකේ ඩ්රොප්වන උපරිම විභවය (එනම් සැපයුම් විභවය) දක්වා ක්රියා කිරීමට හැකි විය යුතුයි පිලිස්සෙන්නේ නැතිව. බලන්න ඉහත කැප් එක යෙදීම නිසා, පරිපථයට විදුලිය සපයා යම් සුලු මොහොතකට පසුවයි උපකරණය ක්රියාත්මක වූයේ.
පළමුවෙන්ම ඔබට අවශ්ය කාල පමාව තීරණය කරන්න. බොහෝවිට තත්පරයක් හෝ ඊට අඩු කාල පමාවක් නම් උචිතයි. අති විශාල කාල පමාවක් අවශ්ය කරන විට, වෙනමම ටයිමර් සර්කිට් එකක් සම්බන්ධ කිරීම වඩා උචිතයි මොකද එවැනි විශාල කාල පමාවන් සඳහා අති විශාල ධාරිතා අගයක් අවශ්ය වේ. මෙවැනි අති විශාල ධාරිතා අගයන් සහිත කැප් සොයා ගැනීමට ප්රායෝගිකව බැරිය. ධාරිතාව ඉහල දැමිය නොහැකි නම්, ප්රතිරෝධී අගය ඉහල දැමිය යුතුය. ඉතා ඉහල ප්රතිරෝධී අගයන් සහිත ප්රතිරෝධක නම් ඕනෑ තරම් තිබේ. එහෙත් එහිදී වෙනත් ප්රශ්නයක් මතු වේ. එනම්, ප්රතිරෝධි අගය ඉහල යන විට, ධාරාව කුඩා වේ. ඉතිං අති විශාල ප්රතිරෝධයක් දැමූ විට, සමහරවිට ඒ හරහා යන ධාරාව උපකරණයට ප්රමාණවත් නොවේ. එනිසයි කුඩා කාල පමාවන් සඳහා පමණක් මෙවැනි සරල ඩිලේ සර්කිට් ප්රයෝජනවත් වන්නේ.
ඉහතදී කාල පමාව තීරණය කළ පසු සුදුසු ධාරිතා හා ප්රතිරෝධි අගයන් තීරණය කළ හැකියි. සාමාන්යයෙන් RC කාල නියත පහකින් ධාරිත්රකය සම්පූර්ණයෙන්ම චාජ් වේ යනුවෙන් සැලකෙනවනෙ. ඉතිං මෙම කාල නියත පහ තුළ ඔබට අවශ්ය කාල පමාව තබා ගන්න. මා යෝජනා කරන්නේ කාල නියත තුනකින් පමණ ඔබට අවශ්ය කාල පමාව ඇති කර ගන්න. උදාහරණයක් ඔස්සේ මෙය බලමු. සිතන්න ඔබට අවශ්යයි මිලිතත්පර 120ක කාල පමාවක් කියා. ඒ කියන්නේ විදුලිය සපයා මිලිතත්පර 120කින් තමයි උපකරණය ඔන් විය යුත්තේ. උපකරණය ක්රියාත්මක වීමට වෝල්ට් 5ක් අවශ්ය යැයි සිතමු. තවද උපකරණයට වෝල්ට් 8ක් දක්වා සැපයිය හැකි යැයිද සිතමු. මෙම උදාහරණය සඳහා කාල පමා (time delay) පරිපථය නිර්මාණය කිරීමට මා RC කාල නියත3ක් පමණක් යොදා ගන්නවා. ඒ කියන්නේ කාල නියත 3 වෙන විට, ධාරිත්රකය දෙපස වෝල්ට් 5 හෝ ඊට වැඩියෙන් ඩ්රොප් වී තිබිය යුතුයි. ඔබ දන්නවා කාල නියත 3කින් ධාරිත්රකය සැපයුම් වෝල්ටියතාවෙන් 83%ක් දක්වා චාජ් වෙනවා. ඔබට අවශ්ය මෙම කාල නියත 3න් අවම වශයෙන් වෝල්ට් 5ක් දක්වා ධාරිත්රකය චාජ් වීමයි. මෙය සිදුවීමට සැපයුම් වෝල්ටියතාව, VS කොපමණ විය යුතුද? එය පහත ආකාරයට තර්ක කර ගණනය කළ හැකියි.
කාල නියත 3කින් ධාරිත්රකය අවම වශයෙන් චාජ් වී තිබිය යුතු වෝල්ටියතාව = 5V
කාල නියත 3කට පසු ධාරිත්රකය චාජ් වී තිබෙන ප්රතිශතය = සැපයුම් විභවයෙන් 83%
83% හෙවත් 0.83කට 5V නම්, 100% ට හෙවත් 1.0 ට වෝල්ට් ගණන =
ඉහත
සම්බන්ධතාව තෘප්ත වන ලෙසට
සුදුසු R
හා
C
අගයන්
තෝරාගන්න.
හිතමු
කැප් එක 10u
යැයි
කියා.
එවිට,
ප්රතිරෝධය
=
0.04/0.00001 = ඕම්
4000
කි.
එවිට,
ප්රතිරෝධය
හරහා යන ධාරාව වන්නේ 5/4000
= මිලිඇම්පියර්
1.25
කි.
ඇත්තටම
ඔබ ගණනය කිරීම සිදු කළ යුත්තේ
අනෙක් පැත්තටයි.
ඒ
කියන්නේ උපකරණයට අවශ්ය ධාරාව
අනුවයි R
තීරණය
කළ යුත්තේ.
ඉන්පසුවයි
C
තීරණය
කරන්නේ.
ඒ
අනුව,
සිතන්න
උපකරණයට අවශ්ය කරන ධාරාව
මිලිඇම්පියර් 5ක්
බව.
එවිට,
යෙදිය
යුතු ප්රතිරෝධයේ අගය වන්නේ,
5/0.005 = ඕම්
1000
වේ.
එවිට,
යෙදිය
යුතු ධාරිත්රකයේ අගය වන්නේ,
0.04/1000 = මයික්රොෆැරඩ්
40කි.
යොදන්නේ
ස්ථාවර විදුලියක් නිසා,
ධාරිත්රකය
කාල නියත 5ක්
යන තුරු චාජ් වී,
එතැන්
සිට පරිපථයට කිසිම බලපෑමක්
නොකර "ඔහේ"
පවතිනවා
(හරියට
ධාරිත්රකයක් එතැන නැහැ වගේ).
එහෙත්
නැවත ධාරිත්රකය ක්රියාත්මක
වනවා පරිපථයට විදුලිය විසන්ධි
කළ විගස.
එවිට,
කැප්
එකේ චාජ් වී තිබෙන විදුලිය
උපකරණයට සපයනවා (හරියට
බැටරියක් ලෙස).
එහෙත්
එම චාජ් එක ඉතා ඉක්මනින්ම බැස
යනවා.
ධාරිත්රකය
තාවකාලික ආරෝපණ ගබඩාවක් කියා
ඔබ දන්නවානෙ.
ඔබට
පේනවා මෙවැනි පරිපථ සඳහා
සාමාන්යයෙන් විශාල ධාරිතා
අගයන් සහිත ධාරිත්රක අවශ්ය
කෙරෙන බව.
මේ
සඳහා ඊකැප් යෙදිය හැකියි.
ඊකැප්වලට
ධන ඍණ භේදය තිබේ.
එහෙත්
මෙහිදී එය ප්රශ්නයක් නොවේ
මොකද මෙවැනි පරිපථවල ධන ඍණ
මාරු වන්නේ නැත.
ඒ
අනුව ඉහත රූපයේ ප්රතිරෝධකය
ඕම් 1000
ලෙසද,
කැප්
එක මයික්රොෆැරඩ් 40
ලෙසද
තැබිය හැකියි.
හරි දැන් බලමු කැප්වලට විදුලිය ගමන් කරන මාර්ගය වෙනස් කිරීමට හැකියාව ලැබෙන්නේ කෙලෙසද කියා. කැප් එකක් යනු සංඛ්යාතය අනුව විචලනය වන ප්රතිරෝධයක් (ෆිල්ටර්වල යොදා ගත්තේ මෙම ගතිගුණයනෙ). ඉතිං අපට පුලුවන් අදාල විදුලි සංඥාවේ සංඛ්යාතය ගැන අවබෝධයක් තිබේ නම්, එම සංඥාවට ඉතාම අඩු ප්රතිරෝධි (ප්රතිභාධක) අගයක් ලැබෙන සේ සුදුසු ධාරිතා අගයක් සහිත ධාරිත්රකයක් යොදන්න. උදාහරණයක් ලෙස පහත රූපය සලකන්න. මෙහි විදුලි සංඥාව ගමන් කිරීමට ඇත්තේ එක් මාර්ගයක් පමණයි (A සිට X දක්වා). එනිසා අනිවාර්යෙන්ම ඒ මඟ ඔස්සේ සංඥාව ගමන් කරාවි.
එහෙත් ඔබට අවශ්ය නම්, එම විදුලි සංඥාව A සිට Y දක්වා ගමන් කරවීමට හැකියි. කළ යුත්තේ කුමක්ද? A-X මාර්ගයට වඩා අඩු ප්රතිරෝධක අගයක් සහිතව A-Y මාර්ගයක් සැකසීමයි. රූපය අනුව A-X මාර්ගය අවම වශයෙන් ඕම් 1000කි (ශ්රේණිගත කිලෝඕම් 1ක ප්රතිරෝධකයක් පවතින නිසා). ඔබට හැකි නම් A-Y මාර්ගය ඕම් 10කට අඩුවෙන් සාදාගන්න එම සංඥා ධාරාව A-Y ඔස්සේ ගමන් කරාවි. ඇත්තටම මෙහිදීත් විදුලි සංඥා ධාරාව සම්පූර්ණයෙන්ම A-Y වල ගමන් නොගනී. තවමත් A-X ඔස්සේ මුල් සංඥා ධාරාවෙන් 10%ක් ගමන් කරයි. A-Y ඔස්සේ සත්ය ලෙසම ගමන් කරන්නේ 90%කි. හැමවිටම වාගේ මෙතැනත් 10% රූල් එක වලංගු වේ. සංඥාවකින් 10% නැති වූවාට එතරම් ගණන් නොගන්න. දැන් ඉතිං කරන්නට තිබෙන්නේ යම් සන්නායකයකින් (වයර් කැබැල්ලකින්) A-Y සම්බන්ධ කිරීමද? එයත් එක්තරා විසඳුමක් විය හැකියි මොකද කුඩා වයර් කැබැල්ලක මිලිඕම් ගණනක්වත් ප්රතිරෝධයක් නොමැති නිසා.
පරිපථ නිර්මාණයේදී වෙනස් වෙනස් අගයන් ලබා දෙන්නේ ප්රතිරෝධකවලට බැවින්, ඉහත සම්බන්ධතාව ප්රතිරෝධක අගය මත තීරණය වන සූත්රයක් ලෙස සකස් කරන විට, පහත ආකාරයේ සූත්රයක් ලිවිය හැකියි. හොඳින් බලන්න. මෙම සූත්රයෙන් කියන්නේ ලබාදෙන මුලු ධාරාවෙන් කොපමණ ප්රමාණයක් R2 සහිත මාර්ගය ඔස්සේ ගලා යනවාද යන්නයි. එහිදී භාග සංඛ්යාවේ (අනුපාතයේ) හරය වන්නේ හැමවිටම ගමන් කරන මාර්ග සියල්ලේම ප්රතිරෝධි අගයන්ගේ එකතුවයි. ලවයට ලියන්නේ තමන්ගේ මාර්ගයේ ප්රතිරෝධි අගය නොවන අනෙක් මාර්ගයේ (හෝ මාර්ග කිහිපයේම) ප්රතිරෝධි අගයයි. ඒ කියන්නේ R2 හරහා ගලන ධාරාව සෙවීමේදී, ලවයට ලියන්නේ R1 මාර්ගයේ ප්රතිරෝධයයි.
ඇත්තම කිව්වොත් සංඥා විදුලියටත් ඉහත සිද්ධිය සිදු වෙනවා. එහෙත් අවසන් ප්රතිඵලය ගත් විට ඉන් විකෘතියක්/වෙනසක් ඇති වන්නේ නැහැ. එය තවදුරටත් පැහැදිලිව පෙන්වන්නම්. සිතන්න ඇම්පියර් 1ක සංඥා විදුලියක් ලබා දෙනවා කියා. එවිට, එම විදුලිය පළමු විභව බෙදුමේදි 1:1 අනුපාතයට බෙදෙනවා. එවිට පළමු කොටසෙන් පිටවන්නේ ඇම්පියර් 0.5ක විදුලියකි. එම 0.5 දැන් දෙවැනි විභව බෙදුමට යෑමෙන් එහිදිත් 1:1 අනුපාතයට අනුව බෙදෙනවා. එවිට, දෙවැනි කොටසින් පිට කරන සංඥා විදුලියේ අගය ඇම්පියර් 0.25කි. එනම්, පරිපථයට අැතුලු කළ ධාරාවෙන් 1/4ක ප්රමාණයක් ලෙස කුඩා වී තමයි සංඥා විදුලිය අවසන් වන්නේ. මෙයම දැන් සත්ය ලෙසම සිදුවන ක්රියාවලිය ඔස්සේ සිතන්න. සංඥා විදුලියට දැන් වෙන වෙනම විභව බෙදුම් කොටස් පෙනෙන්නේ නැත. ඒ වෙනුවට ඉහතදී පෙන්වා දුන් පරිදි ඕම් 100 හා ඕම් 33 ලෙස පවතින තනි විභව බෙදුමක් තමයි පෙනෙන්නේ. ඒ කියන්නේ ඇම්පියර් 1ක සංඥා විදුලියක් ඇතුලු කළ විට, එම විදුලිය 100:33 යන අනුපාතයට බෙදෙනවා. එවිට, ඉන් පිට වන්නේ නැවතත් ඇම්පියර් 0.25ක සංඥාවකි. ඒ කියන්නේ පෙර ගණනය කළ ප්රමාණයමයි. ඒ කියන්නේ සංඥාට මොන විදියට එම පරිපථය විග්රහ කළත් වෙනසක් නැත.
යන
සූත්රය යෙදේ.
යන
සූත්රයයි.
සමහර අවස්ථාවල හර්ට්ස් වලින් මනින සංඛ්යාතය (f) වෙනුවට, “තත්පරයට රේඩියන්" වලින් මනින සංඛ්යාතය (ω) යොදා ගන්නවා. මෙය "කෝණික සංඛ්යාතය" (angular frequency) හෝ "කෝණික ප්රවේගය" (angular velocity) ලෙසද හැඳින්විය හැකියි. සාමාන්ය සංඛ්යාතය හා කෝණික සංඛ්යාතය අතර පහත ආකාරයේ සරල සම්බන්ධතාවකුයි පවතින්නේ. මෙම සරල සම්බන්ධතාව යොදාගෙන ඔබට දැන් පහසුවෙන් එක් සංඛ්යාතයකින් පවතින අගයක් අනෙක් සංඛ්යාතයට හැරවිය හැකියි.
ω = 2πf
මේ අනුව XC = 1/2πfC යන සූත්රයම XC = 1/ωC යනුවෙන්ද ලිවිය හැකියි. තවද, කට්-ඕෆ් සංඛ්යාතය යනු කැප් එකේ ප්රතිභාධක අගය හා රෙසිස්ටරයේ ප්රතිරෝධ අගය සමාන වන තැනයි. ඒ අනුව, කට්-ඕෆ් සංඛ්යාතය අපට පහසුවෙන් පහත ආකාරයට සොයාගත හැකියි.
R = XC → R = 1/2πfCC → fC = 1/2πRC
ඉහත සූත්රයම කෝණික සංඛ්යාතය යොදාගෙන 2πfC = 1/RC → ω = 1/RC ලෙස ලිවිය හැකියි. විවිධ පොත්වල විවිධ ක්රමවලින් දක්වන නිසයි මා මෙවැනි සුලු සුලු කාරණා පවා මතු කරන්නේ. ඒ සියල්ල ගැන දැන සිටීමෙන් ඔබට රසවත්ව හා පහසුවෙන් ඉලෙක්ට්රොනික්ස් උගත හැකි වේවි බොහෝ පතපොත කියවමින්.
පෙර අවස්ථාවක සඳහන් කළා සරල RC සර්කිට් එකක් ෆිල්ටර් සර්කිට් එකක් ලෙස භාවිතා කරන විට, ඩිකේඩ් 1කට ඩෙසිබල් 20ක හායනයක් සිදුවන බව. ඇත්තටම එම ප්රකාශය වඩා පුලුල් වීම පිණිස මා කැමතියි එය තරමක් මෙසේ වෙනස් කරන්නට. කැපෑසිටර් හා ඉන්ඩක්ටර් යනු ප්රතිභාධක අගයන් පෙන්විය හැකි උපාංග දෙකක් (තවම ඉන්ඩක්ටර් ගැන අප ඉගෙන ගෙන නැත). එවැනි ප්රතිභාධකයන් දැක්විය හැකි උපාංග reactive ලෙස හැඳින් වෙනවා. ඒ අනුව, කැප් හා ඉන්ඩක්ටර් රියැක්ටිව් උපාංග දෙකක් වුවත්, රෙසිස්ටරය රියැක්ටිව් නොවේ. යම් ෆිල්ටර් සර්කිට් එකක රියැක්ටිව් උපාංග (එනම්, කැප් හෝ ඉන්ඩක්ටර්) ඇත්තේ එකක් පමණක් නම්, එවැනි ෆිල්ටර් එකක හායනය -20dB/decade වේ. මේ අනුව මෙතෙක් අප සලකා බැලූ HPF හා LPF යන දෙකම -20dB/decade හායනයක් සහිත ෆිල්ටර් වේ. අප ඒ හැම අවස්ථාවකම භාවිතා කළේ එක කැප් එකක් පමණි. මෙවැනි එක් රියැක්ටිව් උපාංගයක් යොදාගෙන සාදනු ලබන ෆිල්ටර් first-order filter (1st order filter) හෝ single-pole filter ලෙස හැඳින්වෙනවා. ඒ කියන්නේ, මෙවැනි රියැක්ටිව් උපාංග දෙකක් යොදාගෙන second-order filter (2nd order filter) හෙවත් two-pole filterද සෑදිය හැකියි. එවිට, ෆිල්ටර් එකේ හායනය තවත් වැඩි වේ (එනම්, ස්ලොප් එක/රෝල්-ඕෆ් එක වැඩි වේ). එනම්, හායනය දෙගුණ වේ (-40dB/decade). මෙලෙස ෆිල්ටර් කොටස් තව තවත් එකතු කර third-order, fourth-order ආදී ෆිල්ටර් සෑදිය හැකියි. ඒ සෑම ෆිල්ටර් කොටසකම -20dB/decade හායනය බැගින් එකතු වේ. මෙලෙස ෆිල්ටර් කොටස් එකතු කළ හැකි ආකාර කිහිපයක් පැවතිය හැකියි. පහත දැක්වෙන්නේ එවැනි සරල සම්බන්ධතාවකි.
ඉහත කර තිබෙන්නේ පළමු ෆිල්ටර් කොටසේ අවුට්පුට් එක දෙවැනි ෆිල්ටර් කොටසට ඇතුලු කිරීම නේද? බැලූබැල්මට මෙවැනි කොටස් රාශියක් එකතු එකතු කර, ෆිල්ටර් එකේ බෑවුම වැඩි කරගෙන ඉස්තරම්ම ෆිල්ටර් එකක් සාදාගත හැකි යැයි සිතුනත්, මෙවැනි සරල ෆිල්ටර්වලට වඩා උසස් තත්වයේ ෆිල්ටර් වෙනත් ක්රමවලින් සාදාගත හැකියි. මෙවැනි ෆිල්ටර්වල හැමවිටම ඉන්පුට් සංඥාවට වඩා අවුට්පුට් සංඥාව කුඩාය; එනම්, වැලැක්විය නොහැකි අනිවාර්ය හායනයක් පවතී. මෙවැනි සරල RC (හා RL හා RCL) ෆිල්ටර් එමනිසා passive filter ලෙස හැඳින්වෙනවා (කිසිදු ඇක්ටිව් උපාංගයක් ෆිල්ටර් තුළ නැති නිසාද පැසිව් යන නම යෙදේ; ඇක්ටිව් හා පැසිව් උපාංග ගැන මොහොතකින් පැහැදිලි කෙරේ). සාමාන්යයෙන් ඉහත වැනි ෆස්ට් ඔ්ර්ඩර් පැසිව් ෆිල්ටර් එහි ඇති සරලකම හා පහසුව නිසාම බහුලව භාවිතා වෙනවා. සෙකන්ඩ් ඕර්ඩර් පැසිව් ෆිල්ටර්ද භාවිතා වෙනවා. සර්කිට් ලෝඩිං වීම ෆිල්ටර් කොටස් කිහිපයක් එකතු කර සාදන පැසිව් ෆිල්ටර්වල ඇති ප්රධානතම ගැටලුවයි. එය වැලැක්විය හැකියි පසු ෆිල්ටර් කොටස්වල ප්රතිරෝධකය ඊට පෙර කොටසේ ප්රතිරෝධකය මෙන් අඩුම ගාණේ දසගුණයක් වැඩි අගයක් යෙදීමෙන්. (මෙය නේද සර්කිට් ලෝඩිං වැලැක්වීමට හැමවිටම යොදාගන්නා කෝකටත් තෛලය?) එනම්, R2 = 10R1, C2 = 10C1, R3 = 10R2, C3 = 10C2 ආදී ලෙස. එහෙත් ප්රායෝගිකව එසේ ප්රතිරෝධ අගයන් දසගුණ කරමින් කොටස් ගණනාවක් එකතු කිරීමේ බාධා ඇත.
ට්රාන්සිස්ටර් හා අයිසී උපයෝගී කරගෙන සංඥාව වර්ධනය කරන ෆිල්ටර් නිපදවිය හැකියි. එවිට, ඉහත සර්කිට් ලෝඩිං ගැටලුව පහසුවෙන්ම අවම කළද හැකියි. ඒවා ගුණාත්මකබවින්ද ඉහළයි. මෙවැනි ෆිල්ටර් active filter ලෙස හැඳින්වෙනවා. ඉහල ඕර්ඩර්වල (higher order) පැසිව් ෆිල්ටර්වලට වඩා ඇක්ටිව් ෆිල්ටර් කොලිටියෙන් වැඩිය.
ඉහත රූපයේ පෙනෙන සෙකන්ඩ් ඕර්ඩර් පැසිව් ෆිල්ටර් එක තරමක් විශ්ලේෂණය කරමු. කට්-ඕෆ් සංඛ්යාතයේදී පළමු RC කොටසින් අවුට්පුට් වන වෝල්ටියතාව වන්නේ ඉන්පුට් වෝල්ටියතාවෙන් 70.7% කි. දැන් දෙවන කොටසේ ෆිල්ටර් එකද ඊට ලැබෙන වෝල්ටියතාවෙන් 70.7% ක් තමයි නැවත එලියට ලබා දෙන්නේ. එය මුල් ෆිල්ටර් කොටසට ලබා දුන් ඉන්පුට් වෝල්ටියතාවට සාපේක්ෂව, 70.7% x 70.7% (හෙවත් 0.707 x 0.707 = 0.499) කි. එය සුලු කළ විට, 49.9% (ආසන්න අගයට ගත් විට, 50%) කි. මේ ආදී ලෙස ඔබට හැකියි තව තවත් ෆිල්ටර් කොටස් එකතු කරන විට, ඒ සියල්ලම විසින් කට්-ඕෆ් සංඛ්යාතයේදී ඉන්පුට් වෝල්ටියතාවෙන් කොපමණ ප්රතිශතයක් පිට කරනවාදැයි ගණනය කිරීමට. එය සූත්රයක් ලෙස (0.707)n ලෙස ලිවිය හැකියි (n යනු ෆිල්ටර් කොටස් ගණනයි). මේ අනුව RC ෆිල්ටර් කොටස් 3ක් සහිත ෆිල්ටරයකින් (0.707)3 = 70.7% x 70.7% x 70.7% = 35% කි.
වෙනස් වෙනස් RC ෆිල්ටර් සර්කිට් දෙකක් හෝ කිහිපයක් ඉහත රූපයේ ආකාරයට සම්බන්ධ කළ හැකියි. එවිට, අප සිතන්නට පෙළඹෙන්නේ මෙසේය. පළමු ෆිල්ටර් කොටසේ ඇති R හා C වල අගයන් මත සුපුරුදු පරිදි කට්-ඕෆ් සංඛ්යාතය හා අනෙකුත් ෆිල්ටර් සාධක තීරණය වන බවත්, එසේ ෆිල්ටර් වෙච්ච සංඥාව තමයි දැන් දෙවැනි ෆිල්ටර් කොටසට අැතුලු වෙන්නේ. දැන් මෙම දෙවැනි ෆිල්ටර් එක වෙනමම සලකා බලනවා. ඒ කියන්නේ දෙවැනි ෆිල්ටර් කොටසේ පවතින R හා C අගයන් මත කට්-ඕෆ් සංඛ්යාතය ආදිය නැවත තීරණය වෙනවා. මේ ආදි ලෙස ඉදිරියට ඇති අනෙක් ෆිල්ටර් කොටස් ගැනද වෙන වෙනම සිතනවා. මෙලෙස සිතීමෙන් කිසිම ප්රශ්නයක් නැහැ මේ සෑම ෆිල්ටර් කොටසකම පවතින කැප්වල අගයන් හා රෙසිස්ටර්වල අගයන් එක සමානයි නම්. එහෙත් සිතන්න පළමු ෆිල්ටර් කොටසේ R හා C අගයන්ට වඩා දෙවැනි ෆිල්ටර් කොටසේ R හා C අගයන් වෙනස් වූවොත් කුමක් සිදු වේවිද? (ඉහත සර්කිට් ලෝඩිං ප්රශ්නය නැති කිරීමට එසේ කරන්නට සිදු වෙනවානේ.) එවිට, පළමු කොටසින් යම් කට්-ඕෆ් සංඛ්යාතයක් සහිතව ෆිල්ටර් වෙච්ච සංඥාව දෙවැනි කොටසට ඇතුලු වී එම දෙවැනි කොටසේදී වෙනත් කට්-ඕෆ් සංඛ්යාතයක් සහිතව ෆිල්ටර් වේ. ඒ කියන්නේ R, C අගයන් වෙනස් වන විට, එක් එක් කොටසේ කට්-ඕෆ් සංඛ්යාත වෙනස් වේ. මේ ආදී ලෙස එක් එක් ෆිල්ටර් කොටසේ කට්-ඕෆ් සංඛ්යාතයන් වෙන වෙනම ගණනය කර, අවසානයේ මේ සියල්ලෙහිම "සමක කට්-ඕෆ්" අගය සෙවිය යුතුය. එම සමක කට්-ඕෆ් සංඛ්යාතය තමයි සම්පූර්ණ ෆිල්ටරයේ කට්-ඕෆ් සංඛ්යාතය ලෙස සලකන්නේ. මෙලෙස එක එක කොටසින් කට්-ඕෆ් සංඛ්යාතයන් වෙනස් වීම ගැන තක්සේරු කිරීම කරදරකාරී වේ. අපට පුලුවන් පහත දැක්වෙන සරල සූත්රයෙන් කොටස් දෙකකින් යුත් සම්පූර්ණ ෆිල්ටර් එකේම කට්-ඕෆ් සංඛ්යාතය සොයා ගන්නට.
ඉහත සූත්රය ෆස්ට් ඕර්ඩර් RC ෆිල්ටර් එකේ කට්-ඕෆ් සංඛ්යාතය සොයන සූත්රය සමග සංසන්දනය කරන්න. දෙකම එකිනෙකට අනුරූප බව පෙනේවි. මෙහිදී ඇත්තටම වී තිබෙන්නේ ෆිල්ටර් කොටස් දෙකේ තිබෙන R1, R2 රෙසිස්ටර් අගයන් දෙක එකට ගුණ කර එහි වර්ගමූලයද, C1, C2 කැප් අගයන් දෙක එකට ගුණ කර එහි වර්ගමූලයද ගැනීමයි. එනම්, විවිධ අගයන් ඇති විට, ඒවායේ යම් "පොදු තනි අගයක්" බවට ඒවා පත් කරගනී. (යම් අගයන් දෙකක් ගුණ කර ඉන්පසු එහි වර්ගමූලය ගැනීම ගණිතයේදී මධ්යනය අගය සොයන එක් ක්රමයක්.) ඉන්පසුව එම මධ්යන්ය අගයන් දෙක සාමාන්ය ෆස්ට් ඕර්ඩර් සූත්රයේ R හා C වලට ආදේශ කළ හැකියි.
ෆිල්ටර් කොටස් තුනක් හෝ වැඩි ගණනක් පවතින අවස්ථාවද මේ ලෙසම තර්ක කර බලන්න. කොටස් තුනක් ඇති අවස්ථාව බලමු. මෙහිදී ප්රතිරෝධක අගයන් තුන එකට ගුණ කර, තුන්වෙනි මූලයද, ධාරිත්රක තුනේ අගයන් එකට ගුණ කර, තුන්වෙනි මූලයද ගත යුතුය. මේ ආදී ලෙස ගත යුතු මූලය ඕර්ඩර් එකට සමාන වේ. ඕනෑම ඕර්ඩර් එකක් සඳහා පහත ආකාරයට පොදු සූත්රයක් ලිවිය හැකියි. ප්රතිරෝධක n ගණනක් ඇති විට, ඒ සියලු ප්රතිරෝධක අගයන් එකට ගුණ කර ලැබෙන පිළිතුරෙහි n වැනි මූලය සොයන්න. එලෙසම කැප්වලටත් කරන්න. ඉන්පසු එම අගයන් සාමාන්ය කට්-ඕෆ් සංඛ්යාතය සොයන සූත්රයට ආදේශ කරන්න. මෙම සූත්රය ගැන කල්පනා කළ යුත්තේ අන්න ඒ ලෙසටයි. අමුතුවෙන් පාඩම් කරන්නට දෙයක් මෙහි නැත.
කොටස් දෙකක් සම්බන්ධ කර සාදන සෙකන්ඩ් ඕර්ඩර් පැසිව් ෆිල්ටර් එකක ෆිල්ටර් වීම පෙන්වන ප්රස්ථාරයක් පහත රූපයේ දැක්වේ. නිල්පාට වක්රයෙන් පෙන්වන්නේ පළමු කොටස පමණක් තිබෙන විට ෆිල්ටරයේ බෑවුමයි. දම්පාටින් පෙන්වන්නේ කොටස් දෙකම තිබෙන විට ෆිල්ටරයේ බෑවුමයි. තවද, ෆිල්ටර් කොටස් දෙකේ යෙදෙන R හා C අගයන් වෙනස් වීම නිසා, කට්-ඕෆ් සංඛ්යාතයට එය බලපා ඇති අයුරුත් මෙහි පේනවා. එනම්, කට්-ඕෆ් සංඛ්යාතය තරමක් වෙනස් වී (පස්සට ගොස්) ඇත.
ඉහත LPF සඳහා සෙකන්ඩ් ඕර්ඩර් පැසිව් RC ෆිල්ටර් සර්කිට් නිර්මාණය කරන ආකාරයටමයි HPF වල ඉහල ඕර්ඩර් ෆිල්ටර් සාදන්නේ. සූත්රද වෙනස් නොවේ. එවැනි HPF සෙකන්ඩ් ඕර්ඩර් ෆිල්ටර් පරිපථයක් පහත දැක්වේ.
ඉහත HPF හා LPF ෆිල්ටර් දෙකක් එකට කනෙක්ට් කිරීමෙන් බෑන්ඩ්පාස් ෆිල්ටර් සෑදීමට හැකියි (පහත රූපය). දැන් බලමු බෑන්ඩ්පාස් ෆිල්ටර් එකක් එලෙස සාදා ගන්නා අයුරු. කට්-ඕෆ් සංඛ්යාත දෙක පළමුව තීරණය කළ යුතුයි. ඉන් අපර් කට්-ඕෆ් සංඛ්යාතය තමන්ගේ කට්-ඕෆ් සංඛ්යාතය ලෙස යොදා ගත් ලෝපාස් ෆිල්ටර් එකක්ද, ලෝවර් කට්-ඕෆ් සංඛ්යාතය තමන්ගේ කට්-ඕෆ් සංඛ්යාතය ලෙස යොදා ගත් හයිපාස් ෆිල්ටර් එකක්ද ශ්රේණිගතව සම්බන්ධ කරන්න.
එවිට, අවශ්ය සංඛ්යාත පරාසය පමණක් ගමන් කරවනවා එම පරාසයට පිටින් තිබෙන සංඛ්යාත ෆිල්ටර් කරමින්. පැහැදිලිවම බෑන්ඩ්පාස් ෆිල්ටර් එකක් යනු ස්වභාවයෙන්ම සෙකන්ඩ් ඕර්ඩර් ෆිල්ටරයකි මොකද එම ෆිල්ටරයේ රියැක්ටිව් උපාංග (කැප්) දෙකක් යොදාගෙන තිබෙනවා. බෑන්ඩ්පාස් ෆිල්ටරයක බෝඩ් ප්ලොට් එක පහත දැක්වේ.
උදාහරණයක් ගෙන බලමු. හර්ට්ස් 20ත් කිලෝහර්ට්ස් 20ත් අතර සංඛ්යාත පමණක් යෑමට සලස්වන බෑන්ඩ්පාස් ෆිල්ටරයක් සාදමු. මෙහිදී ෆිල්ටරය කොටස් දෙකක් ලෙස සලකා සැලසුම් කළ යුතුයි. එකක් නම් හර්ට්ස් 20ට අඩු සංඛ්යාත ෆිල්ටර් කර දමන HPF එකක් වන අතර, අනෙක හර්ට්ස් 20,000ට වැඩි සංඛ්යාත ෆිල්ටර් කර දමන LPF කි. මේ දෙක පෙර ඔබ උගත් පරිදි ගණනය කරන්න.
ඉහත බෑන්ඩ්පාස් ෆිල්ටර් සර්කිට් එකේ C1, R1 දෙක එක්ව සාදන්නේ HPF ක් කියා බැලූ බැල්මට පෙනේ. එහි කට්-ඕෆ් සංඛ්යාතය 20 වේ. ඔබ දන්නවා දැන් ෆිල්ටරයේ ප්රතිරෝධක/සම්භාදක අගය සොයන්නේ මෙම ෆිල්ටරය කනෙක්ට් කරන අනෙක් පරිපථ කොටස් අනුව බව. උපකල්පනය කරමු R1 = 1000 ohm හා R2 = 10000 ohm ලෙස තිබිය යුතුයි කියා. ඒ අනුව, කැප් එකේ අගය ගණනය කරන්න. එලෙසම C2, R2 එක්ව සාදන්නේ LPF යි. මෙහි කට්-ඕෆ් සංඛ්යාතය වන්නේ හර්ට්ස් 20,000 වේ. එහිදිත් කැප් එකේ අගය ඔබට ගණනය කරන්න පුලුවන්නෙ. ඔබට C1= 8u හා C2= 0.8n ලෙස ලැබෙනවාද බලන්න ඔබේ ගණනය කිරීම් මඟින්?
ඇත්තටම ඉහත බෑන්ඩ්පාස් ෆිල්ටරය ගුණාත්මකබවින් නම් එතරම් ඉහල නැත. පසුවට ඉගැන්වෙන ක්රම යොදාගෙන ඉස්තරම් වර්ගයේ (ඇක්ටිව්) ෆිල්ටර් වර්ග සාදා ගත හැකියි. මෙවැනි බෑන්ඩ්පාස් ෆිල්ටර් කිහිපයක් එකට එකතු කර (ඕර්ඩර් එක ඉහල දැමීමෙන්) බෑවුම වැඩි කරගත හැකියි.
ඉහත ලෝපාස්, හයිපාස්, බෑන්ඩ්පාස් ආදි ලෙස නම් කෙරුණු ෆිල්ටර්ම විවිධ අවස්ථාවල යෙදෙන අතර, සමහර වෙලාවට ඒ ඒ අවස්ථාවේ නමින්ද එම ෆිල්ටර් හැඳින්වෙනවා. hiss filter, pop filter, treble-cut filter, bass-cut filter, hum filter ආදී ලෙස ඔබට මේවා දැක ගත හැකියි. උදාහරණයක් ලෙස, ට්රෙබල් කට් ෆිල්ටර් එකක් යනු ලෝපාස් ෆිල්ටරයකි. එම ෆිල්ටරයෙන් සිදු කෙරෙන්නේ ශබ්දයක අධිසංඛ්යායන් ඉවත් කිරීමයි (ශබ්දයක අධිසංඛ්යාතයන් treble යනුවෙන් හැඳින්වෙනවා). එලෙසම ශබ්දයක බේස් (bass යනු ශබ්දයක අවසංඛ්යාතයන්ය) කැපීමට යොදාගන්නා බේස් කට් ෆිල්ටරය හයිපාස් ෆිල්ටරයකි.
ඔබේ නිවසට ලැබෙන ප්රධාන විදුලිය (mains electricity) හර්ට්ස් 50ක සංඛ්යාතයක් සහිත ඒසී විදුලියකි (ඇමෙරිකාව වැනි සමහර රටවල එය හර්ට්ස් 60 වේ). හර්ට්ස් 50ක සංඥාවක් යනු කනට ඇසෙන "ශ්රව්ය පරාසයේ" (20Hz – 20kHz) පවතින්නකි. එය බේස් ශබ්දයකි; ඝෝෂාකාරියි (ඇත්තටම ඔබ හර්ට්ස් 50 හා 60 ඝෝෂාවක් අසන්න එම ඝෝෂාව කෙබදුද කියා වටහගැනීමට; CoolEdit/Audition වැනි පරිගණක සොෆ්ට්වෙයාර් එකකින් ඕනෑම සංඛ්යාතයක ශබ්දයක් ඔබට නිර්මාණය කළ හැකියි). ඉතිං සමහර අවස්ථාවල විවිධ ක්රම මඟින් මෙම ප්රධාන විදුලි සංඛ්යාතය සර්කිට් එක හරහා යන සංඥාව හා මුසු වේ. ඒ විතරක් නොවේ මෙම සංඛ්යාතයේ දෙගුණය (හර්ට්ස් 100 හෝ 120) ද එලෙසම කරදරකාරි ලෙස මුසු වේ. මෙන්න මෙවැනි ප්රධාන විදුලිය නිසා ඇති වන හර්ට්ස් 50/100 (හෝ 60/120) ඝෝෂාව හඳුන්වන්නේ "හම්" (hum) එක කියාය. මෙම ඝෝෂාව කනට ඇසෙන්නේ "හ්ම්ම්ම්ම්" ලෙස නිසයි මෙම නම ඊට ලැබී ඇත්තේ. මෙම හම් ඝෝෂාව ෆිල්ටර් කිරීමට යොදන හම් ෆිල්ටරය යනු බෑන්ඩ්ස්ටොප් ෆිල්ටරයකි (එනම්, හර්ට්ස් 50/100 හෝ 60/120 සංඛ්යාත පමණක් ෆිල්ටර් කරයි).
සටහන
කනට ඇසෙන්නේ හර්ට්ස් 20ත් 20,000ත් අතර සංඛ්යාතයන්ගෙන් යුතු ශබ්ද පමණක් බව ඔබ දැන් දන්නවා. හර්ට්ස් 20ට අඩු ශබ්ද infrasound (අධෝධ්වනි) ලෙසද, හර්ට්ස් 20000ට වැඩි ශබ්ද ultrasound (අතිධ්වනි) ලෙසද හැඳින්වෙනවා. ඇත්තටම සෑම මනුස්සයෙකුටම මෙම සම්පූර්ණ පරාසය තුළ සියලු ශබ්ද ඇසෙන්නේ නැත. ක්රමයෙන් වයසට යන විට, ක්රමයෙන් මෙම පරාසය පටු වෙනවා. (ඒ කියන්නේ උඩ හා යට සීමාවන් එකිනෙකට ළං වෙනවා. උදාහරණයක් ලෙස, වයස 65 පමණ වන විට සමහරවිට හර්ට්ස් 40ත් 18000ත් අතර පරාසය දක්වා පටු විය හැකියි). එහෙත් සමහර සතුන්ට ඉහත සංඛ්යාතවලින් පිටත ශබ්ද පවා ඇසිය හැකියි (වවුලන්, තල්මසුන්, බල්ලන් වැනි සතුන්ට).
විද්යාවේදී "ශබ්දයේ සංඛ්යාතය" යන වචනය භාවිතා කළත්, සංගීතයේදී හා ශබ්ද විද්යාවේදී (acoustics) මීට pitch (තාරතාව) කියාද පවසනවා. මෙම ශ්රව්ය පරාසය තුළ ඉහළ පිච් (high pitch) ශබ්ද හැඳින්වෙන්නේ treble (උච්ච ස්වරය) ලෙස වන අතර, පහල පිච් (low pitch) ශබ්ද හැඳින්වෙන්නේ bass (මන්ද්ර ස්වරය) ලෙසයි. ට්රෙබල් හා බේස් ශබ්දවලට හරියටම අහවල් අහවල් සංඛ්යාත පරාස තිබේ යැයි සම්මතයක් නැත. දළ වශයෙන් බේස් යනු හර්ට්ස් 200ට අඩු සංඛ්යාත (එනම්, හර්ට්ස් 20ත් 200ත් අතර) ලෙසද, ට්රෙබල් යනු හර්ට්ස් 4000ට වැඩි සංඛ්යාත (එනම්, හර්ට්ස් 4000ත් 20000ත් අතර) ලෙසද මතක තබා ගන්න. එවිට, හර්ට්ස් 200ත් 4000ත් අතර සංඛ්යාත කලාපයටද midrange ලෙස නමක් ලබා දේ.
සාමාන්යයෙන් හොඳ සවුන්ඩ් සිස්ටම් එකක ස්පීකර් ගණනාවක් පවතින්නේ ඉහත හේතුව නිසාමයි. එක් ස්පීකරයකින් ඉතා හොඳ ගුණාත්මක බවින් යුතු ශබ්දයක් ඇති කළ නොහැකියි සම්පූර්ණ ශ්රව්ය සංඛ්යාත පරාසය පුරාම. එනිසා ප්රධාන ලෙස ස්පීකර් වර්ග 3ක් නිපදනවා. ඉන් එකක් tweeter කියා හැඳින්වෙනවා. මෙම ස්පීකර් අනෙක් ඒවාට වඩා කුඩාය. ට්රෙබල් ශබ්ද ඉතා හොඳින් මෙම ට්වීටර් හරහා පිට කළ හැකියි. මෙම ස්පීකර්වලට බේස් හෝ මිඩ්රේන්ජ් ශබ්ද යවන්න නරකයි. එලෙසම woofer ලෙසද ස්පීකර් වර්ගයක් තිබෙනවා. මෙම ස්පීකර් අනෙක් ඒවාට වඩා විශාලයි. බේස් ශබ්ද සඳහායි වූෆර් සාදා තිබෙන්නේ. මිඩ්රේන්ජ් සංඛ්යාත ශබ්ද සඳහා සාමාන්ය ප්රමාණයේ midrange ස්පීකර් නිපදවා තිබෙනවා. මේ එක් එක් ස්පීකරය සඳහා ඊට සුදුසු සංඛ්යාත පරාසයන් පමණක් යොමු කළ යුතු වෙනවා. එය සිදු කරන්නේද ෆිල්ටර් හරහාය. සාමාන්ය ශබ්දය ලෝපාස් ෆිල්ටරයක්, හයිපාස් ෆිල්ටරයක්, බෑන්ඩ්පාස් ෆිල්ටරයක් යන තුන් වර්ගයේම "ෆිල්ටර් සෙට් එකක්" හරහා යවනවා. එහිදී ඒ ඒ ෆිල්ටර්වලින් පිටවන තරංග ඉහත ස්පීකර් වර්ග තුනට වෙන වෙනම ලබා දෙනවා. ඇත්තටම ඉහත "ෆිල්ටර් සෙට් එක" crossover network ලෙසයි හැඳින්වෙන්නේ.
ඒ විතරක් නොවේ, එම ඇසෙන සංඛ්යාත පරාසය තුළ සෑම ශබ්දයක්ම එකම ආකාරයට දැනෙන්නේද නැත. සාමාන්යයෙන් සංඛ්යාතය ඉහළට යන විට ශබ්දයේ සැර වැඩියෙන් දැනේ. මෙහෙම සිතන්න. සිතමු වොට් 1ක ජවයක් ඇති හර්ට්ස් 100ක ශබ්දයකුයි වොට් 1ක ජවයක් ඇති හර්ට්ස් 10000ක ශබ්දයකුයි ඔබට ඇසෙනවා කියා. දෙකේම ජවය (ශක්තිය) සමානයි. එහෙත් ඔබේ කනට දැනෙන්නේ හර්ට්ස් 10000 ශබ්දය ඉතා වැඩි ශබ්දයක් සහිත ලෙසයි. ඇත්ත වශයෙන්ම ශබ්ද දෙකේම ශක්තිය සමානයි. එහෙත් මෙතැන සිදු වී ඇත්තේ ඉහළට යන සංඛ්යාතයන්ට කන ක්රමයෙන් සංවේදී වැඩි වීමයි. මෙන්න මෙම මූලික ප්රශ්නය නිසා තමයි සංගීතයේදී සවුන්ඩ් මික්සිං කරන්නට සිදුවන්නේ. උදාහරණයක් ලෙස, ඉහල සංඛ්යාතයක් සහිත සංගීත භාණ්ඩයේ හඬ පහල සංඛ්යාතයක් සහිත සංගීත භාණ්ඩයේ හඬට වඩා කැපී පෙනේ. එවිට රසය අඩු වේ. එමනිසා sound mixing මඟින් මේවා ගාණට "බැලන්ස්" කළ යුතුයි.
සංගීත නිර්මාණයේදී ලොකු ස්ටූඩියෝ ඇතුලේ බරපතල කාර්යක් ලෙස ඉහත සවුන්ඩ් මික්සිං සිදු කරනවා. ඔබද මෙම දේම එක්තරා විදියකට සිදු කරනවා ඔබේ ප්ලේයර් එකෙන්. බේස් කොන්ට්රෝල්, ට්රෙබල් කොන්ට්රෝල්, ඊක්වලයිසර් ආදීය තිබෙන්නේ මේ සඳහාය. ට්රෙබල් කන්ට්රෝලර් එක කරකවා ට්රෙබල් ශබ්ද අඩු වැඩි කළ හැකියි. එලෙසම බේස් කන්ට්රෝලර් එක කරකවා බේස් ශබ්ද අඩු වැඩි කළ හැකියි. ඊක්වලයිසර් එකේ විවිධ ස්ලයිඩර්/නොබ් කරකවා සංඛ්යාත පරාසයකම ශබ්දවල සැර වෙන් වෙන්ව වෙනස් කළ හැකියි. ඊක්වලයිසර් එකක් යනු ශ්රව්ය සංඛ්යාත පරාසය තුල යම් ක්රමවත් ක්රමයකට තෝරාගත් සංඛ්යාත හත අටක පමණ ශබ්දයේ සැර/හඬ අඩු වැඩි කළ හැකි පරිදි සෑදූ ෆිල්ටර් සමූහයකි. ඔව්, ඊක්වලයිසර් එකක් යනු ෆිල්ටර් සෙට් (a set of filters) එකක්.
සටහන
විදුලි සංඥා ගැන කතා කරන හැමවිටම වාගේ (විශේෂයෙන් ෆිල්ටර් ගැන කතා කිරීමේදී) සංඛ්යාතය ගැනද කතා කෙරෙනවා. යම් සංඛ්යාතයක දෙගුණය, තුන්ගුණය, දසගුණය ආදී ලෙස "ගුණාකාරයන්" (multiples) ගැනද අපට කතා කළ හැකියි. උදාහරණයක් ලෙස, හර්ට්ස් 100 ගනිමු. එහි දෙගුණය හර්ට්ස් 200 වේ; තුන්ගුණය 300ද, දොලොස්ගුණය 1200ද වේ. පොදුවේ "ගුණාකාරය" (multiple) යන වචනය භාවිතා කළද, විද්යා හා තාක්ෂණයේදී "උපරිතාන" (overtone) යන නම ඊට භාවිතා කෙරේ. ඒ අනුව, හර්ට්ස් 200 හි පළමු උපරිතානය 400ද, දෙවැනි උපරිතානය 600ද වේ. සලකා බලනු ලබන මුල් සංඛ්යාතය "මූලික සංඛ්යාතය" (fundamental frequency) ලෙස හැඳින්වෙනවා.
ඇයි උපරිතාන ගැන අප උනන්දු විය යුත්තේ? ඊට වැදගත් හේතුවක් තිබේ. සමහර පරිපථවල නිතර සිදුවන දෙයක් තමයි යම් විදුලි සංඥාවක සංඛ්යාතයේ විවිධ උපරිතාන ඉබේම නිපැදවීම. එය ඇත්තටම ගැටලුවක්. ඒ කියන්නේ හර්ට්ස් 1000ක සංඥාවක් ගමන් කරන විට, ඒ සමගම හර්ට්ස් 2000, 3000, ආදී සංඥා ඇති වේ. හැමවිටම මෙලෙස සෑදෙන උපරිතාන මූලික සංඛ්යාතය සහිත සංඥාවට වඩා බොහෝ දුර්වලයි (එනම් උපරිතාන සංඥාවල ජවය, ධාරාව, හා වෝල්ටියතාව ඉතාම අඩුයි). උදාහරණයක් ලෙස, වෝල්ට් 1ක සංඥාවේ උපරිතාන සංඥාවක වෝල්ට් ගණන මිලිවෝල්ට් 1ක් පමණ විය හැකියි. ඔබ ඉහතදී දුටුවා ප්රධාන විදුලිය නිසා ඇති වන හම් එක ගැන විස්තරය. එහි විදුලි සංඛ්යාතයට අමතරව පළමු උපරිතානයද ඇතිවන බව දැන් වටහගන්න.
දැනට ෆිල්ටර් ගැන හොඳටම ප්රමාණවත්. දැන් බලමු කැපෑසිටරයක් හා රෙසිස්ටරයක් උපයෝගී කරගෙන සරල delay circuit එකක් සාදාගන්නා අයුරු. ඩිලේ සර්කිට් එකක් යනු විදුලිය සපයපු මොහොතේම ක්රියාත්මක නොවී, විදුලිය සපයා යම් සුලු මොහොතකට පසුව ක්රියාත්මක වන පරිදි සර්කිට් එකකි. මෙහිදී පරිපථය සාමාන්යයෙන් විචලනය නොවන ඩීසී විදුලියකටයි සම්බන්ධ කරන්නේ. එය සෑදීම ඉතාම පහසුයි (පහත රූපය).
මෙහි උපයෝගි කරගෙන තිබෙන්නේ කැපෑසිටර් චාජ් වීමේ ක්රියාවයි. ඔබ දන්නවා කැප් එකක් චාජ් වන වේගය තීරණය කරන්නේ එහි කැපෑසිටන්ස් එක හා ඊට ශ්රේණිගතව සම්බන්ධ කර තිබෙන රෙසිස්ටරයේ (හෝ ප්රතිරෝධයක් දැක්විය හැකි ඕනෑම "කොටසක") ප්රතිරෝධි අගය මතයි. T = RC යන කාල නියතය ගැන මතක් කර ගන්න. ඉහත රූපයේ IN කොටසට විචලනය නොවන විදුලියක් ලබා දෙන විට, එම විදුලිය ධාරිත්රකයට "උරා ගන්නවා" (එනම් ධාරිත්රකය දෙපස ඩ්රොප් වෙනවා). කැප් එක ක්රමයෙන් චාජ් වෙනවා. එවිට එය දෙපස ඩ්රොප් වන විභවයද ක්රමයෙන් ඉහල යනවා (එය ඉහල යන්නේ ධාරිත්රකයේ සුපුරුදු ඝාතීය ශ්රිතයේ ස්වරූපයෙන්). OUT යන කොටසට සම්බන්ධිත උපකරණය ක්රියාත්මක වීමට යම් නිශ්චිත අවම වෝල්ටියතාවක් අවශ්යයි. ඉතිං ධාරිත්රකයේ දෙපස ඩ්රොප් වන විභවයනෙ එම උපකරණයට ලබා ගන්නේ (අවුට්පුට් කරන්නේ). IN කොටසට විදුලිය ලබා දුන් පළමු අවස්ථාවේදී ධාරිත්රකයේ විභවය ශූන්යයි. එහෙත් එය ක්රමයෙන් චාජ් වෙනවා (ඝාතීය ලෙස). එලෙස චාජ් වෙමින්, ධාරිත්රකය දෙපස ඉහත උපකරණයට අවශ්ය අවම වෝල්ටියතාව ඩ්රොප්වන විටම, එම උපකරණය ක්රියාත්මක වෙනවා. තවදුරටත් කැප් එක සමහරවිට චාජ් වේවි. එවිට, විභවය තව තවත් ඉහල යාවි. එනිසා සවි කරන උපකරණය කැප් එකේ ඩ්රොප්වන උපරිම විභවය (එනම් සැපයුම් විභවය) දක්වා ක්රියා කිරීමට හැකි විය යුතුයි පිලිස්සෙන්නේ නැතිව. බලන්න ඉහත කැප් එක යෙදීම නිසා, පරිපථයට විදුලිය සපයා යම් සුලු මොහොතකට පසුවයි උපකරණය ක්රියාත්මක වූයේ.
පළමුවෙන්ම ඔබට අවශ්ය කාල පමාව තීරණය කරන්න. බොහෝවිට තත්පරයක් හෝ ඊට අඩු කාල පමාවක් නම් උචිතයි. අති විශාල කාල පමාවක් අවශ්ය කරන විට, වෙනමම ටයිමර් සර්කිට් එකක් සම්බන්ධ කිරීම වඩා උචිතයි මොකද එවැනි විශාල කාල පමාවන් සඳහා අති විශාල ධාරිතා අගයක් අවශ්ය වේ. මෙවැනි අති විශාල ධාරිතා අගයන් සහිත කැප් සොයා ගැනීමට ප්රායෝගිකව බැරිය. ධාරිතාව ඉහල දැමිය නොහැකි නම්, ප්රතිරෝධී අගය ඉහල දැමිය යුතුය. ඉතා ඉහල ප්රතිරෝධී අගයන් සහිත ප්රතිරෝධක නම් ඕනෑ තරම් තිබේ. එහෙත් එහිදී වෙනත් ප්රශ්නයක් මතු වේ. එනම්, ප්රතිරෝධි අගය ඉහල යන විට, ධාරාව කුඩා වේ. ඉතිං අති විශාල ප්රතිරෝධයක් දැමූ විට, සමහරවිට ඒ හරහා යන ධාරාව උපකරණයට ප්රමාණවත් නොවේ. එනිසයි කුඩා කාල පමාවන් සඳහා පමණක් මෙවැනි සරල ඩිලේ සර්කිට් ප්රයෝජනවත් වන්නේ.
ඉහතදී කාල පමාව තීරණය කළ පසු සුදුසු ධාරිතා හා ප්රතිරෝධි අගයන් තීරණය කළ හැකියි. සාමාන්යයෙන් RC කාල නියත පහකින් ධාරිත්රකය සම්පූර්ණයෙන්ම චාජ් වේ යනුවෙන් සැලකෙනවනෙ. ඉතිං මෙම කාල නියත පහ තුළ ඔබට අවශ්ය කාල පමාව තබා ගන්න. මා යෝජනා කරන්නේ කාල නියත තුනකින් පමණ ඔබට අවශ්ය කාල පමාව ඇති කර ගන්න. උදාහරණයක් ඔස්සේ මෙය බලමු. සිතන්න ඔබට අවශ්යයි මිලිතත්පර 120ක කාල පමාවක් කියා. ඒ කියන්නේ විදුලිය සපයා මිලිතත්පර 120කින් තමයි උපකරණය ඔන් විය යුත්තේ. උපකරණය ක්රියාත්මක වීමට වෝල්ට් 5ක් අවශ්ය යැයි සිතමු. තවද උපකරණයට වෝල්ට් 8ක් දක්වා සැපයිය හැකි යැයිද සිතමු. මෙම උදාහරණය සඳහා කාල පමා (time delay) පරිපථය නිර්මාණය කිරීමට මා RC කාල නියත3ක් පමණක් යොදා ගන්නවා. ඒ කියන්නේ කාල නියත 3 වෙන විට, ධාරිත්රකය දෙපස වෝල්ට් 5 හෝ ඊට වැඩියෙන් ඩ්රොප් වී තිබිය යුතුයි. ඔබ දන්නවා කාල නියත 3කින් ධාරිත්රකය සැපයුම් වෝල්ටියතාවෙන් 83%ක් දක්වා චාජ් වෙනවා. ඔබට අවශ්ය මෙම කාල නියත 3න් අවම වශයෙන් වෝල්ට් 5ක් දක්වා ධාරිත්රකය චාජ් වීමයි. මෙය සිදුවීමට සැපයුම් වෝල්ටියතාව, VS කොපමණ විය යුතුද? එය පහත ආකාරයට තර්ක කර ගණනය කළ හැකියි.
කාල නියත 3කින් ධාරිත්රකය අවම වශයෙන් චාජ් වී තිබිය යුතු වෝල්ටියතාව = 5V
කාල නියත 3කට පසු ධාරිත්රකය චාජ් වී තිබෙන ප්රතිශතය = සැපයුම් විභවයෙන් 83%
83% හෙවත් 0.83කට 5V නම්, 100% ට හෙවත් 1.0 ට වෝල්ට් ගණන =
වේ.
එහි
අගය 6.024
කි.
දළ
වශයෙන් 6V
ලෙස
ගත හැකියි.
ඒ
කියන්නේ සැපයුම් වෝල්ටියතාව
වෝල්ට් 6ක්
විය යුතුය.
උපකරණයට
වෝල්ට් 8ක්
දක්වා ලබා දිය හැකි නිසා උපකරණය
පිලිස්සෙන්නේ නැත.
ඔබට
මෙලෙසද කළ හැකියි.
සැපයුම්
වෝල්ටියතාව 5V
ලෙසම
ගත හැකියි.
ධාරිත්රකය
වෝල්ට් 5
දක්වා
චාජ් වීමට කාල නියත 5ක්
ගන්නවා.
ඒ
කියන්නේ කාල නියත 3ක්
වෙනුවට 5ම
ඔබ දැන් යොදාගන්නවා.
මේ ආදී
ලෙස කාල නියතයන් හා සැපයුම්
වෝල්ටියතාවන් නිශ්චය කළ
හැකියි.
මෙම
උදාහරණයේදී අප යොදාගත්තේ කාල
නියත 3ක්
පමණක් නිසා,
ඒ ඔස්සේ
ඉදිරියට ගණනය කිරීම් කරගෙන
යමු.
ඔබට
අවශ්ය කාලය මිලිතත්පර 120කි.
කාල
නියත තුනක් සඳහාම මිලිතත්පර
120
නිසා,
එක්
RC
කාල
නියතයක් සඳහා 120/3
= මිලිතත්පර
40
වේ.
ඒ
කියන්නේ,
R
(ohm) x C (Farad) = 0.04 (Second) වේ.
පරිපථ
තුළ විදුලි සංඥා ගමන් කරනවා.
විදුලි
සංඥාවක් හැමවිටම විචලනය වන
කුඩා විදුලියක් (වෝල්ටියතාවක්/ධාරාවක්).
විදුලි
සංඥා අපට අවශ්ය මාර්ග ඔස්සේ
ගමන් කරවීමට කැපෑසිටර් යොදා
ගන්නවා.
මෙහෙම
සිතන්න.
ඔබට
ගමන් බිමන් යෑමට පාරවල් සාදා
තිබෙනවා.
පාරවල්
තිබූ පලියට ඔබ ඒ හැම මාර්ගයකින්ම
ගමන් කරන්නේ නැහැ නේද?
ඔබට
අවශ්ය ගමනාන්තය දක්වා ගමන්
කිරීමට උචිත මාර්ග පමණයි ඔබ
තෝරා ගන්නේ.
එහිදී
පහසුවෙනුත් ඉක්මනිනුත් යා
හැකි මාර්ග ඔබ තීරණය කරනවා.
මහ
පොලව මත විවිධ තැන්වල මාර්ග
සාදා තිබෙන්නේ විවිධ හේතු
නිසා.
ඔබ
පමණක් නොවේ ගමන් කරන්නේ.
මිනිසුන්
බොහෝ ගණනකගේ අවශ්යතා සැපිරෙන
ලෙසටත් පාරවල් සාදා තිබෙන්නේ.
විදුලි
සංඥාත් එබදුයි.
පරිපථය
තුළ සංඥාවලට යෑමට හැකි මාර්ග
බොහෝ ගණනක් තිබේ.
ට්රාන්සින්ටර්
බයස් කිරීම,
වෙනත්
උපාංගවලට විදුලි බල සැපයුම
ලබා දීමට ආදී නොයෙක් හේතු මත
පරිපථය තුළ විදුලිය ගමන් කළ
හැකි පාරවල් (වයර්/ප්රින්ට්)
බොහෝ
ගණනක් තිබෙනවා.
ඒ තිබූ
පලියට සංඥාවන්ට ගමන් කළ හැකි
සෑම පාරක් ඔස්සේම "රෝන්දෙ"
ගසන්නට
ඉඩ දිය නොහැකියි.
ඔබට
අවශ්ය මාර්ගය දිගේ පමණක්
සංඥා යැවීමට ධාරිත්රක බහුලව
යොදා ගන්නවා.
පහත
රූපය බලන්න.
ඊට
ඉන්පුට් කරන සංඥාවට යා හැකි
මාර්ග කීයක් තිබේද?
පරිපථ
කොටස ඉතාම සරල නිසා පහසුවෙන්ම
පේනවා මාර්ග දෙකක් පවතින බව.
පරිපථ
කොටස සරල වුවත් සංකීර්ණ වුවත්
අනිවාර්යෙන්ම එක් රීතියක්
වලංගු වෙනවා.
ඒක
තමයි,
යම්
විදුලියක් (හෝ
විදුලි සංඥාවක්)
සඳහා
අත්යවශ්යයෙන්ම මාර්ග/පින්
දෙකක් තිබෙනවා.
එකකින්
විදුලිය/සංඥාව
එලියට යවා අනෙකෙන් නැවත එය
ලබා ගන්නවා (එහෙමත්
නැතිනම් එකකින් විදුලිය/සංඥාව
ලබාගෙන අනෙකන් එය එලියට යවනවා).
ඒ නිසානේ
"පරිපථ"
යන
නමත් ඊට ලැබෙන්නේ (මේ
ගැන මීට පෙර හොඳින් විස්තර
කර ඇත).
ඉතිං
පහත පරිපථ කොටසේ විදුලිය ගමන්
කරන්නේ කුමන මාර්ගයේද?
පෙරත්
සඳහන් කළ ලෙසම විදුලිය ගමන්
කළ යුත්තේ අපට අවශ්ය (අප
කියන)
මාර්ගයේය.
එහෙත්
විදුලියට අප කටින් කියන
උපදෙස්වලින් වැඩක් නැහැ.
ඊට
තේරෙන භාෂාවක් ඇත.
විදුලිය
ගමන් කළ යුත්තේ අහවල් මාර්ගය
ඔස්සේ යැයි අප උපදෙස් දෙන්නේ
විදුලියට තේරෙන "ප්රතිරෝධකතාව"
ඔස්සේය.
එනම්,
A නම්
පාරේ නොයා B
නම්
පාරේ ගමන් කරන්න කියා අප ඊට
උපදෙස් දෙන්නේ A
මාර්ගයේ
(සන්නායකයේ)
ප්රතිරෝධ
අගය ඉහල දමා හා B
පාරේ
ප්රතිරෝධ අගය පහල දැමීමෙනි.
A පාරේ
පොඩ්ඩක්වත් නොයන්න කියා කීමට
එම පාරේ ප්රතිරෝධ අගය අනන්තය
දක්වා ඉහල දමන්න;
ඒ
කියන්නේ එම පාර වසා දමන්න;
ඒ
කියන්නේ එම සන්නායක පාරේ
සන්නායක කොටස් ගලවා දමන්න.
ඉතිං
ප්රතිරෝධ අගයන් වෙනස් කිරීමෙන්
අපට පුලුවන් නේද අපට කැමති
කැමති පාරවල් ඔස්සේ සංඥා දැන්
යැවීමට?
හරි දැන් බලමු කැප්වලට විදුලිය ගමන් කරන මාර්ගය වෙනස් කිරීමට හැකියාව ලැබෙන්නේ කෙලෙසද කියා. කැප් එකක් යනු සංඛ්යාතය අනුව විචලනය වන ප්රතිරෝධයක් (ෆිල්ටර්වල යොදා ගත්තේ මෙම ගතිගුණයනෙ). ඉතිං අපට පුලුවන් අදාල විදුලි සංඥාවේ සංඛ්යාතය ගැන අවබෝධයක් තිබේ නම්, එම සංඥාවට ඉතාම අඩු ප්රතිරෝධි (ප්රතිභාධක) අගයක් ලැබෙන සේ සුදුසු ධාරිතා අගයක් සහිත ධාරිත්රකයක් යොදන්න. උදාහරණයක් ලෙස පහත රූපය සලකන්න. මෙහි විදුලි සංඥාව ගමන් කිරීමට ඇත්තේ එක් මාර්ගයක් පමණයි (A සිට X දක්වා). එනිසා අනිවාර්යෙන්ම ඒ මඟ ඔස්සේ සංඥාව ගමන් කරාවි.
එහෙත් ඔබට අවශ්ය නම්, එම විදුලි සංඥාව A සිට Y දක්වා ගමන් කරවීමට හැකියි. කළ යුත්තේ කුමක්ද? A-X මාර්ගයට වඩා අඩු ප්රතිරෝධක අගයක් සහිතව A-Y මාර්ගයක් සැකසීමයි. රූපය අනුව A-X මාර්ගය අවම වශයෙන් ඕම් 1000කි (ශ්රේණිගත කිලෝඕම් 1ක ප්රතිරෝධකයක් පවතින නිසා). ඔබට හැකි නම් A-Y මාර්ගය ඕම් 10කට අඩුවෙන් සාදාගන්න එම සංඥා ධාරාව A-Y ඔස්සේ ගමන් කරාවි. ඇත්තටම මෙහිදීත් විදුලි සංඥා ධාරාව සම්පූර්ණයෙන්ම A-Y වල ගමන් නොගනී. තවමත් A-X ඔස්සේ මුල් සංඥා ධාරාවෙන් 10%ක් ගමන් කරයි. A-Y ඔස්සේ සත්ය ලෙසම ගමන් කරන්නේ 90%කි. හැමවිටම වාගේ මෙතැනත් 10% රූල් එක වලංගු වේ. සංඥාවකින් 10% නැති වූවාට එතරම් ගණන් නොගන්න. දැන් ඉතිං කරන්නට තිබෙන්නේ යම් සන්නායකයකින් (වයර් කැබැල්ලකින්) A-Y සම්බන්ධ කිරීමද? එයත් එක්තරා විසඳුමක් විය හැකියි මොකද කුඩා වයර් කැබැල්ලක මිලිඕම් ගණනක්වත් ප්රතිරෝධයක් නොමැති නිසා.
සටහන
විභව බෙදුම් පරිපථයක විභවය බෙදෙන අනුපාතය අනුව එක් එක් ප්රතිරෝධකයේ පිහිටන වෝල්ටියතාවන් පහසුවෙන් ගණනය කරන්නට ඔබ දන්නවා (VO = VI x(R1/(R1+R2) සූත්රය අනුව).
විභව බෙදුම් පරිපථයක විභවය බෙදෙන අනුපාතය අනුව එක් එක් ප්රතිරෝධකයේ පිහිටන වෝල්ටියතාවන් පහසුවෙන් ගණනය කරන්නට ඔබ දන්නවා (VO = VI x(R1/(R1+R2) සූත්රය අනුව).
විභවය
පමණක් නොව ධාරාවට ගලා යා හැකි
මාර්ග කිහිපයක් තිබෙන විට,
ධාරාවද
යම් අනුපාතයකින් එම මාර්ගවලට
බෙදී යනවා.
(KCL හි
ඇත්තටම මෙය තමයි සලකා බලන්නේ).
වෝල්ටියතාව
බෙදී යෑමේදී වැඩි ප්රතිරෝධි
අගය සහිත ප්රතිරෝධයේ තමයි
වැඩිපුර වෝල්ටියතාවක් රඳවාගන්නේ.
එහෙත්
ධාරාව සැලකීමේදී ඊට ප්රතිවිරුද්ධ
දේ සිදුවෙනවා.
එනම්,
අඩු
ප්රතිරෝධයක් තිබෙන කොටස
හරහා තමයි වැඩි ධාරාවක් ගමන්
කරන්නේ (ඕම්
නියමය අනුව එය පැහැදිලියිනෙ).
පහත
රූපය බලන්න.
මුලු
ධාරාව (It)
I1 හා
I2
ලෙස
බෙදී යනවා.
මෙම
බෙදී යන අනුපාතය කුමක්ද?
ප්රතිරෝධ
දෙකෙහි අනුපාතයන්ගේ විලෝමය
අනුවයි ඒවා බෙදී යන්නේ.
ඒ
කියන්නේ මෙහි R1
හි අගය
R2හි
අගයට වඩා සියගුණයකින් වැඩි
නම්,
R2 හරහා
ගලා යන ධාරාව R1
හරහා
ගලා යන ධාරාවට වඩා සියගුණයකින්
වැඩිය.
ඒ අනුව
පහත රූපයේ දැක්වෙන පරිපථ කොටස
සඳහා It
= I1 + I2 → It = I1 +
100I1 වේ.
පරිපථ නිර්මාණයේදී වෙනස් වෙනස් අගයන් ලබා දෙන්නේ ප්රතිරෝධකවලට බැවින්, ඉහත සම්බන්ධතාව ප්රතිරෝධක අගය මත තීරණය වන සූත්රයක් ලෙස සකස් කරන විට, පහත ආකාරයේ සූත්රයක් ලිවිය හැකියි. හොඳින් බලන්න. මෙම සූත්රයෙන් කියන්නේ ලබාදෙන මුලු ධාරාවෙන් කොපමණ ප්රමාණයක් R2 සහිත මාර්ගය ඔස්සේ ගලා යනවාද යන්නයි. එහිදී භාග සංඛ්යාවේ (අනුපාතයේ) හරය වන්නේ හැමවිටම ගමන් කරන මාර්ග සියල්ලේම ප්රතිරෝධි අගයන්ගේ එකතුවයි. ලවයට ලියන්නේ තමන්ගේ මාර්ගයේ ප්රතිරෝධි අගය නොවන අනෙක් මාර්ගයේ (හෝ මාර්ග කිහිපයේම) ප්රතිරෝධි අගයයි. ඒ කියන්නේ R2 හරහා ගලන ධාරාව සෙවීමේදී, ලවයට ලියන්නේ R1 මාර්ගයේ ප්රතිරෝධයයි.
DC හා AC Analysis සහ Passive හා Active Devices
එහෙත්
බොහෝ අවස්ථා තිබෙනවා එලෙස
නිකංම වයර් කැබැල්ලක් පමණක්
සවි කළ නොහැකි වන.
ඒකට
හේතුවක් තිබෙනවා.
පරිපථයක
හැමවිටම වාගේ විදුලි වර්ග
දෙකක් හමු වෙනවා.
එකක්
නම් සංඥාවේ විදුලියයි.
මෙම
සංඥා විදුලිය අත්යවශ්යයෙන්ම
විචලනය වන විදුලියක්.
මෙම
සංඥා විදුලිය තමයි ප්රමුඛ
වන්නේ සර්කිට් එකක.
එම
සංඥා විදුලියට විවිධ දේවල්
පරිපථ විසින් සිදු කරනවා.
සංඥා
විදුලිය පරිපථයකට ඉන්පුට්
(ඇතුලු)
කළාට
පසුව එක් එක් ඉලෙක්ට්රොනික්
උපාංගයක් හරහා අවසානයේ පරිපථයෙන්
අවුට්පුට් වෙනකල් ගමන් කරනවා.
අප ඉහත
කතා කළේ මෙන්න මෙම සංඥා විදුලිය
ගමන් කරන මාර්ගය ගැනයි.
එහෙත්
මෙම සංඥා විදුලියට අමතරව තවත්
විදුලියක් තිබෙනවා පරිපථවල.
එය
අත්යවශ්යයෙන්ම ස්ථායි ඩීසී
විදුලියකි.
රෙසිස්ටර්,
කැපෑසිටර්,
ඉන්ඩක්ටර්
වැනි සමහර උපාංග තිබෙනවා
කෙලින්ම සංඥා විදුලිය සමග
පමණක් වුවද වැඩ කළ හැකි.
මෙවැනි
ඉලෙක්ට්රොනික් උපාංග passive
උපාංග
ලෙස හැඳින්වෙනවා.
එහෙත්
ඉතා වටිනා හෝ සංකීර්ණ දේවල්
සිදු කරන ට්රාන්සිස්ටර්,
අයිසී
වැනි උපාංග නිවැරදිව ක්රියාත්මක
වීමට වෙනමම භාහිර ඩීසී විදුලියක්
ඒ උපාංගවලට වෙන වෙනම ලබා දිය
යුතුයි.
එය
හරියට වාහනයකට තෙල් ගානවා
බදුය.
වාහනයක්
තිබ්බට වැඩක් නැහැනේ තෙල්
නැතිනම්.
ට්රාන්සිස්ටර්වලට
මෙලෙස සුදුසු ඩීසී විදුලිය
ලබා දීම හඳුන්වන්නේ ට්රාන්සිස්ටරයක්
බයස් කරනවා යනුවෙනි.
අයිසීවලට
නම් පින් දෙකක් හෝ වැඩි ගණනක්
තිබෙනවා එලෙස භාහිර ඩීසී
විදුලිය ලබා දීමට (එහෙත්
අයිසී බයස් කරනවා කියා වචනයක්
නැත).
ක්රියාත්මකවීමට
මෙලෙස භාහිර ඩීසී විදුලියක්
අවශ්ය කරන උපාංග active
උපාංග
ලෙස හැඳින්වෙනවා.
ඉතිං
සුදුසු ස්ථාවර ඩීසී විදුලිය
සපයා ක්රියාකාරී මට්ටමේ
තිබෙන ඇක්ටිව් උපාංගවලට සංඥා
විදුලියද යොමු කරනවා.
එවිට,
එම
උපාංග මඟින් තමන් වෙතට යොමු
කරපු සංඥා විදුලියට අවශ්ය
වෙනස්කම් සිදු කරනවා.
(මේ
ගැන සම්පූර්ණ විස්තර ට්රාන්සිස්ටර්
පාඩම්වල දැක්වේවි).
දැන්
අප ඉදිරියේ තිබෙන ගැටලුව
මෙයයි.
ප්රථමයෙන්ම,
රෙසිස්ටර්
සුදුසු ලෙස යොදා ගනිමින් අප
ඇක්ටිව් උපාංග සියල්ලම සුදුසු
ක්රියාකාරි මට්ටමේ තබනවා.
ඒ
කියන්නේ ඒ ඒ ඇක්ටිව් උපාංගයට
අවශ්ය විදුලිය (වෝල්ටියතාව
හා ධාරාව)
අප
ප්රතිරෝධක මඟින් සාදා ගනු
ලබන විභව බෙදීම් යොදා ගනිමින්
සෙට් කරනවා (ඉහතදී
විස්තර කළ විභව බෙදුම් පරිපථ
ගැන හොඳ අවබෝධයක් ලබා සිටිය
යුතු ප්රධාන කාරණය මෙයයි).
එවිට,
විභව
බෙදුම් පරිපථ කොටස් ගණනාවක්
(සමහරවිට
සිය ගණනක් වුවද)
පරිපථයේ
අඩංගු වේවි.
එහෙත්
එම පරිපථ කොටස් හැම එකක් හරහාම
සංඥා විදුලිය ගමන් කරවන්නේ
නැහැ.
ඒකනේ
ඉහතදී පැවසුවේ අපට අවශ්ය
මාර්ගයේ පමණක් සංඥාව යැවීමට
සිදු වෙනවා කියා.
ඉතිං
ඒ සඳහා ඉහත අප පැමිණි එක්
විසඳුමක්නෙ නිකංම අඩු ප්රතිරෝධී
අගයන් සහිත සන්නායක/වයර්
යොදා අපට අවශ්ය මාර්ගයට සංඥාව
යොමු කිරීම.
එහෙත්
එසේ කළ නොහැකියි.
නිකංම
වයර් කොටස් සම්බන්ධ කළොත්
ඉන් ඇක්ටිව් උපාංගවලට යෙදූ
ඩීසී විදුලි මට්ටම් වෙනස්
වෙනවා මොකද සන්නායක/ප්රතිරෝධක
තුළින් ඩීසී මෙන්ම විචලනය වන
විදුලිය (ඒසීද
ඇතුලත්)
යන
දෙකම ගමන් කරනවා.
මෙය
තමයි සර්කිට් ලෝඩිං ලෙසින්
අපට නිතරම කරදර කරන්නේ.
අපට
ඇත්ත වශයෙන්ම අවශ්ය කරන්නෙ
පරිපථයේ ඩීසී විදුලි මට්ටම්
අවුල්/වෙනස්
නොකරන එහෙත් විචලනය වන විදුලිය
පමණක් වෙනස් කරන ක්රමවේදයක්.
දැන්
එකවර සිහියට එන ඉලෙක්ට්රොනික්
උපාංගය කුමක්ද?
ධාරිත්රකය
නේද?
ධාරිත්රක
හරහා ස්ථාවර ඩීසී විදුලිය
ගමන් නොකර විචලනය වන විදුලිය
පමණක් ගමන් කරවනවා.
පහත
රූපය බලන්න.
මොහොතකට
සිතන්න A-B
ලෙස
දක්වා ඇති සන්නායක කොටස නැතැයි
කියා.
තවද,
යම්කිසි
අත්යවශ්ය කරුණක් නිසා ස්ථාවර
ඩීසී විදුලිය වෙනස් නොවී තිබිය
යුතු යැයිද උපල්පනය කරන්න
(එනම්,
A ස්ථානයේ
වෝල්ට් 5ක්ද
B
ස්ථානයේද
වෝල්ට් 5ක්
තිබිය යුතු යැයි සිතමු).
දැන්
පරිපථය සැලසුම් කර තිබෙන්නේ
එම කොන්දේසිවලට යටත්වයි.
එවිට,
මෙහි
R1
හා R2
ගත්
විට,
එතැන
තිබෙන්නේ විභව බෙදුමකි.
ඉන්පුට්
වෝල්ටියතාව වෝල්ට් 10
නම්,
දැන්
R2
හරහා
වෝල්ට් 5ක්
ඩ්රොප් වී ඇත (ඒ
කියන්නේ A
හි
වෝල්ටි 5ක්
තිබෙනවා ඉහත කොන්දේසිය
සපුරමින්).
එලෙසම
R3
හා R4
යන
කොටසත් වෙනම ගත් විට,
එතැනත්
තිබෙන්නේ විභව බෙදුමකි.
එහිත්
R4
හරහා
වෝල්ට් 5ක්
ඩ්රොප්වනු ඇත (B
ස්ථානයේ
වෝල්ට් 5ක්
තිබෙනවා කොන්දේසිය සපුරමින්).
මේ කතා
කළේ සංඥා විදුලිය ගැන නොව,
ස්ථාවර
ඩීසී විදුලිය ගැනයි.
දැන්
සිතන්න IN
එකට
සංඥා විදුලිය ඇතුලු කරනවා
කියා.
එවිට,
එම
සංඥා විදුලියද සුපුරුදු ලෙසම
R1-R2
විභව
බෙදුමෙන් ධාරාව
බෙදී යයි.
එහෙත්
මෙම කොටසේ සිට ඊළඟ කොටසට සංඥාව
යැවීම සඳහා ඉහත පෙන්වා ඇති
ආකාරයට A-B
සන්නායකයකින්
දැන් සම්බන්ධ කරනවා යැයි
සිතන්න.
අවශ්ය
නම් නිකංම සන්නායක කොටසක්
වෙනුවට එතැනට රෙසිස්ටරයක්
වුවද සම්බන්ධ කළ හැකියි.
සංඥාව
ගැන නැවත සිත යොමු කරන්න.
දැන්
පළමු විභව බෙදුමෙන් පිට කළ
සංඥාවට තවත් R3-R4
විභව
බෙදුමක් හමු වේ.
මෙහිදී
එම විභව බෙදුමේ අනුපාතය අනුව
නැවත සංඥා විදුලිය (ධාරාව) බෙදේ.
එහෙත්
දැන් ස්ථාවර ඩීසී විදුලියට
කුමක් වේද?
සම්පූර්ණයෙන්ම
එය විකෘති වෙනවා.
ඊට
හේතුව සිතාගත හැකිද?
A ස්ථානයට
ඊට පසුව ඇති කොටසේ R3-R4
ප්රතිරෝධක
කොටස පවතින්නේ සමාන්තරගතවයි.
ධාරාවක්
යම් තැනකින් කොටස්වලට බෙදී
යනවා නම් එතැන ඇත්තේ සමාන්තර
සම්බන්ධතාවක්.
ඒ අනුව
A
සිට
ධාරාවක් B
වෙත
ගලා යන විට,
එම
ධාරාව R3
හා R4
ඔස්සේ
දෙකට බෙදී යනවා.
ඒනිසා
R3-R4
දෙක
සමාන්තරවයි පවතින්නේ.
එම
ප්රතිරෝධක දෙකේ සමක අගය දැන්
ගන්න.
මෙම
උදාහරණයේ එම ප්රතිරෝධක අගයන්
දෙක සමාන නිසා,
සමක
අගය ඉන් භාගයක් ලෙස ගත හැකියි
(එනම්,
සමක
අගය ඕම් 50කි).
දැන්
R3-R4
ප්රතිරෝධක
දෙක වෙනුවට තනි ඕම් 50ක
සමක ප්රතිරෝධයක් (Rx)
එතැන
ඇතැයි සිතන්න (පහත
රූපය).
මෙහිදී
Rx
ප්රතිරෝධකය
හා R2
ප්රතිරෝධකය
නැවතත් සමාන්තරගත විදියට නේද
පිහිටා තිබෙන්නේ?
ඒ
කියන්නේ සත්ය ලෙසම ඕම් 100යේ
R1
ප්රතිරෝධකයට
යටින් පිහිටන්නේ R2-Rx
යන
සමාන්තරගතව පිහිටි ප්රතිරෝධක
දෙකෙහි සමක අගයයි.
එම
දෙකෙහි සමක අගය ඕම් 33
කි.
එවිට,
100:33 යන
අනුපාතයයි පවත්න්නේ.
එම
අලුත් අනුපාතය අනුව A
ස්ථානයේ
විභවය 10
x (33/(33+100) හෙවත්
ඩීසී වෝල්ට් 2.5කි.
මෙය
පෙර සඳහන් කොන්දේසිය කැඩීමක්
නේද?
කොන්දේසිය
අනුව A
හි
අනිවාර්යෙන්ම වෝල්ට් 5ක
ස්ථාවර වෝල්ටියතාවක් පැවතිය
යුතුයි.
ඇත්තම කිව්වොත් සංඥා විදුලියටත් ඉහත සිද්ධිය සිදු වෙනවා. එහෙත් අවසන් ප්රතිඵලය ගත් විට ඉන් විකෘතියක්/වෙනසක් ඇති වන්නේ නැහැ. එය තවදුරටත් පැහැදිලිව පෙන්වන්නම්. සිතන්න ඇම්පියර් 1ක සංඥා විදුලියක් ලබා දෙනවා කියා. එවිට, එම විදුලිය පළමු විභව බෙදුමේදි 1:1 අනුපාතයට බෙදෙනවා. එවිට පළමු කොටසෙන් පිටවන්නේ ඇම්පියර් 0.5ක විදුලියකි. එම 0.5 දැන් දෙවැනි විභව බෙදුමට යෑමෙන් එහිදිත් 1:1 අනුපාතයට අනුව බෙදෙනවා. එවිට, දෙවැනි කොටසින් පිට කරන සංඥා විදුලියේ අගය ඇම්පියර් 0.25කි. එනම්, පරිපථයට අැතුලු කළ ධාරාවෙන් 1/4ක ප්රමාණයක් ලෙස කුඩා වී තමයි සංඥා විදුලිය අවසන් වන්නේ. මෙයම දැන් සත්ය ලෙසම සිදුවන ක්රියාවලිය ඔස්සේ සිතන්න. සංඥා විදුලියට දැන් වෙන වෙනම විභව බෙදුම් කොටස් පෙනෙන්නේ නැත. ඒ වෙනුවට ඉහතදී පෙන්වා දුන් පරිදි ඕම් 100 හා ඕම් 33 ලෙස පවතින තනි විභව බෙදුමක් තමයි පෙනෙන්නේ. ඒ කියන්නේ ඇම්පියර් 1ක සංඥා විදුලියක් ඇතුලු කළ විට, එම විදුලිය 100:33 යන අනුපාතයට බෙදෙනවා. එවිට, ඉන් පිට වන්නේ නැවතත් ඇම්පියර් 0.25ක සංඥාවකි. ඒ කියන්නේ පෙර ගණනය කළ ප්රමාණයමයි. ඒ කියන්නේ සංඥාට මොන විදියට එම පරිපථය විග්රහ කළත් වෙනසක් නැත.
පරිපථයක්
තුළ ඉහත පැහැදිලි කළ ආකාරයේ
විදුලි වර්ග දෙක DC
(ස්ථාවර
විදුලිය)
හා AC
(සංඥා
විදුලිය)
ලෙසයි
හැඳින්වෙන්නේ.
ඉතිං
සෑම පරිපථයක්ම විශ්ලේෂණය කරන
විට දෙයාකාරයකින් එය කළ හැකියි.
එකක්
නම් ඩීසී විදුලිය කොහොමද
පරිපථය තුළ හැසිරෙන්නේ කියන
එක.
එයට
DC
Analysis (ඩීසී
විශ්ලේෂණය)
ලෙස
පැවසෙනවා.
අනෙක
නම් ඔබට දැනටමත් සිතාගත හැකි
පරිදි AC
Analysis වේ.
එලෙසම,
පරිපථයක්
නිර්මාණය කරන විටත්,
මෙම
පැතිකඩ දෙක ගැන වෙන වෙනම
සැලකිලිමත් වීමට සිදු වෙනවා
(ඉහතදී
කළේ මේ දෙක ගැන සැලකිලිමත්වීම
තමයි).
ඒ
විතරක්ද නෙමේ;
ඒසී
හා ඩීසී විදුලි දෙක වෙන වෙනම
දැක්වීමට අප යම් නිරූපණ ක්රමත්
උපයෝගී කොට ගන්නවා.
සාමාන්යයෙන්
ඩීසී විදුලි රාශින් කැපිටල්
අකුරින්ද,
ඒසී
රාශින් සිම්පල් අකුරින්ද
දක්වනවා.
උදාහරණ
ලෙස,
යම්
උපාංගයකට යොදන ඩීසී වෝල්ටියතාව
කැපිටල් වී අකුරින් (V)
දක්වන
අතර,
ඒසී
වෝල්ටියතාව සිම්පල් වී අකුරින්
(v)
දක්වනවා.
එලෙසම
ඩීසී රාශින්,
I (ධාරාව),
P (ජවය),
R (ප්රතිරෝධය)
ලෙසද,
ඒසී
රාශින්,
i (ධාරාව),
p (ජවය),
r (ප්රතිරෝධය)
ලෙසද
දැක්වෙනවා.
ඩීසී
රාශින්/අගයන්
Large
Signal රාශින්/අගයන්
ලෙසත් ඒසී රාශින්/අගයන්
Small
Signal රාශින්/අගයන්
හෝ Incremental
රාශින්/අගයන්
ලෙසත් හැඳින්වෙනවා.
මේ
අනුව,
ඩීසී
විශ්ලේෂණයේදී සෑම කැපෑසිටර්
එකක්ම නැතැයි සිතනවා පමණක්
නොවේ,
කැප්
එක තිබෙන විදුලි කොටසම
සම්පූර්ණයෙන්ම නොසලකා හරිනවා.
කැප්
එක යනු පාලමකට උපමා කළොත්,
එය
හරියට පාලම කඩා දැමුවාක් බදුය.
එවිට
පාලම හරහා එහා මෙහා යා නොහැකියිනේ.
ඒ අනුව
අපේ මුල් ප්රශ්නයට නැවත යොමු
වෙමු.
එනම්,
සංඥා
ගමන් කරවීමට වයර් කැබැල්ලකින්
අලුත් අඩු ප්රතිරෝධයක් සහිත
පාරක් සාදනවා වෙනුවට,
ධාරිත්රකයක්
යොදා එම පාර සෑදිය යුතු වෙනවා.
පරිපථය
නිර්මාණය කරන කෙනා දන්නවා
ගමන් කරන සංඥාවේ සංඛ්යාතය
(එනම්,
ගමන්
කරන සංඥාවේ උපරිම හා අවම
සංඛ්යාතයන් දෙක).
ඒ අනුව
ධාරිත්රක ප්රතිභාදක සූත්රය
යොදාගෙන සංඥාවේ සංඛ්යාතයන්ට
අඩු ප්රතිරෝධිතාවක් ලැබෙන
සේ යෙදිය යුතු ධාරිත්රකයේ
අගය නිර්ණය කළ හැකියි.
ඉහත
උදාහරණය නැවත සලකා බැලුවොත්
ධාරිත්රකයේ ප්රතිභාදකය
උපරිම වශයෙන් ඕම් 100
විය
යුතුය.
එම
පරිපථයේ ගමන් කරන සංඥාවේ
සංඛ්යාතය හර්ට්ස් 10000
ලෙස
සිතමු.
එවිට,
යෙදිය
යුතු ධාරිත්රකයේ අගය වන්නේ,
මෙවැනි
අරමුණකින් (එනම්
සිග්නල් එකක් ගමන් කරන මාර්ගය
වෙනස් කිරීම හෙවත් සිග්නල්
එකක් තවත් තැනකට යොමු කිරීම)
ධාරිත්රකයක්
යොදා ගන්නා විට,
එම
ධාරිත්රකය coupling
capacitor ලෙස
හැඳින්වෙනවා.
බොහෝවිට
ඉතා කුඩා ධාරිතා අගයන් සහිත
ධාරිත්රක තමයි මේ සඳහා යොදා
ගන්නේ.
එනිසා
හොඳ කොලිටියෙන් යුත් සෙරමික්
හෝ පොලිමර් ෆිල්ම් ධාරිත්රක
යොදන්න.
මා
දැක තිබෙනවා මෙවැනි තැන්වලට
අනවශ්ය මෙන්ම කිසිසේත්
නුසුදුසු ඊකැප් පවා යොදනවා.
සංඥා
විදුලියක් යනු ඒසී විදුලියක්
බදුයි.
ඉතිං
එවැනි කැප් සුදුසු නැති බව
ඊකැප් ගැන සාකච්ඡා කළ අවස්ථාවේදීත්
සඳහන් කළා.
එහෙත්
බැරිවෙලාවත් විශාල ධාරිතාවක්
සහිත කැප් යෙදීමට සිදු වුවොත්
නම් ඊකැප් යෙදීම හැර වෙන කරන්න
දෙයක් නැති වෙනවා.
එහෙත්
ඒවා පවා යෙදිය හැක්කේ එක්
කොන්දේසියක් මතයි.
එනම්
ඒසී විදුලියේ (හෙවත්
සංඥා විදුලිය)
පීක්
වෝල්ටේජ් එක (VP)
වෝල්ට්
එකට වඩා අඩු විය යුතුයි.
එසේ
නොවුණොත් ඊකැප් එක පිලිස්සී
යාවි.
බලන්න
කප්ලිං කැප් එකක් විසින්ද
සිදු කරන්නේ සුපුරුදු ෆිල්ටර්
ක්රියාවලියක්.
ධාරිත්රකයත්
ප්රතිරෝධකයත් අතර විභව
බෙදුමක් තමයි එහි ඇති වෙන්නේ.
ට්රාන්සිස්ටර්
ආදිය සමග තමයි මේවායේ නියම
ප්රයෝජනය දිස් වන්නේ (එහෙත්
ට්රාන්සිස්ටර් ගැන තවම අප
එතරම් කතා කර නොමැති නිසා වැඩි
දුර විස්තර කරන්න බලාපොරොත්තු
නොවේ).
පරිපථ
සාමාන්යයෙන් නිර්මාණය කරන්නේ
අධියරෙන් (stage)
අධියරයටයි.
හරියට
තට්ටු ගොඩනැඟිල්ලක් සාදානවා
බදුය.
ඉතිං
එක් ස්ටේජ් එකකින් අවුට්පුට්
වන සිග්නල් එක ඊට පසු ස්ටේජ්
එකට ඉන්පුට් කරන්නේ බොහෝවිට
මෙවැනි කප්ලිං කැප් එකක්
හරහාය.
ඒසී
විදුලිය "කප්ල්"
(couple යන
ඉංග්රිසි වචනයේ විවිධ තේරුම්
අතර එකක් තමයි "දෙකක්
එකට සම්බන්ධ කරනවා"
යන්න)
කරනවා
යනුවෙන් පවසන විට,
එහි
තවත් දෙයක් සිදුවෙනවා නේද?
එය
තමයි ඩීසී විදුලිය බ්ලොක්
කිරීම.
එම
අරුතින් ගෙන,
ඉහත
කප්ලිං කැප් එකම DC-blocking
cap ලෙසත්
හැඳින්වෙනවා.
ඉහත
පෙන්වා දුන්නේ අත්යවශ්ය
සංඥාව අවශ්ය මාර්ග ඔස්සේ
යැවීමට කප්ලිං කැප් භාවිතා
කරන හැටියි.
ඔබ
දන්නවා සංඥාව සමග විවිධ ඝෝෂාද
ගමන් කරනවා.
එම
ඝෝෂා සාමාන්යයෙන් ඉවත් කරනවා
(ෆිල්ටර්
මඟින්).
අධිසංඛ්යාත
ඝෝෂා (hissing)
ඉවත්
කිරීමට ලෝපාස් ෆිල්ටරයක්
භාවිතා කළ හැකියි.
අවසංඛ්යාත
ඝෝෂා (humming,
popping) ඉවත්
කිරීමට හයිපාස් ෆිල්ටරයක්
භාවිතා කළ හැකියි.
ඇත්තටම
මෙහිදී වන්නේ,
සංඥාව
සමග මුසුව ඇති ඝෝෂාවට අඩු
ප්රතිරෝධි අගයක් සහිත පහසු
පාරක් සාදා දීමයි.
එවිට,
එම
ඝෝෂාව පමණක් සංඥාවෙන් වෙන්ම
එම අඩු ප්රතිරෝධි මඟ ඔස්සේ
ගමන් කරනවා.
ප්රායෝගිකව
මෙහිදී සිදු වන්නේ සංඥාවෙන්
ඝෝෂාව ගලවා තවදුරටත් පරිපථය
ඔස්සේ ඉදිරියට එය ගමන් කිරීමට
ඉඩ නොදෙනු පිණිස එම ඝෝෂාව
ග්රවුන්ඩ් එකට ෂෝට් කිරීමයි.
එවිට,
“හැරෙන
තැපෑලෙන්ම ඝෝෂාව ආපසු හැරවේ".
හැබැයි
මෙහිදී එම කාර්ය සිදු කළ කැප්
එක decoupling
cap ලෙස
හැඳින්වෙනවා (ඩිකප්ල්
යනු කප්ල් යන්නෙහි විරුද්ධ
තේරුමයි;
එනම්
සම්බන්ධව ඇති දෙකක් වෙන් කිරීම
යන තේරුම decouple
යන්නට
ඇත).
ඇත්තටම
මෙයත් ඉහත කතා කළ කප්ලිං කැප්
එකේ වැඩේමයි නේද කළේ?
එහෙනම්
ඇයි ඊට සපුරා විරුද්ධ තේරුම
සහිත නමකින් එය හැඳින්වෙන්නේ?
ඊට
සරල පිළිතුරක් ඇත.
කප්ලිං
කැප් යොදන්නේ සංඥාව ගමන්
කරවීමටයි.
එහිදී
තවදුරටත් සංඥාව නිවැරදි මඟකටයි
සෙට් කළේ.
එහෙත්
ඩිකප්ලිං කැප් යොදන්නේ ඝෝෂාව
ගමන් කරවීමටයි.
එහිදී
ඝෝෂාව පරිපථයෙන් ගලවා දැමීමමයි
සිදු කළේ.
මේ
දෙක හඳුනා ගැනීමට තවත් ක්රමයක්
ඇත.
කප්ලිං
කැප් එකක් සංඥාව ගමන් කරන
මාර්ගයට ශ්රේණිගතවයි සම්බන්ධ
වන්නේ (මොකද
සංඥාවට පාලමක් විදියටයි එය
පවතින්නේ).
එහෙත්
ඩිකප්ලිං කැප් එකක් හැමවිටම
සංඥාව ගමන් කරන මාර්ගයට
සමාන්තරගතව පවතිනවා (මොකද
එය සංඥාව ගමන් කරන මාර්ගෙන්
ග්රවුන්ඩ් එකටයි හැමවිටම
සම්බන්ධ වන්නේ).
ඩිකප්ලිං
කැප්වලටමයි bypass
cap කියා
පවසන්නෙත් (බයිපාස්
යන්නෙහි තේරුම "වෙනත්
මඟක යෑම"
යන්නයි).
ඩිජිටල්
සර්කිට්වල ඔබට බොහෝ කැප් තිබෙන
දැකිය හැකි වෙනවා.
පරිගණකයක
මදර්බෝඩ් එකක් ගෙන බලන්න.
සිය
ගණන් කැප් පෙනෙනු ඇත.
ඔබ
දන්නවාද මේ කැප් සියල්ලම වාගේ
ඩිකප්ලිං කැප්.
ඊට
හේතුව ඩිජිටල් ඉලෙක්ට්රොනික්ස්
පාඩම්වලදී පෙන්වා දෙන්නම්.
ඉලෙක්ට්රෝනික්ස් (electronics) ...
ඉලෙක්ට්රෝනික්ස් (electronics) ...

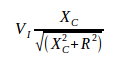














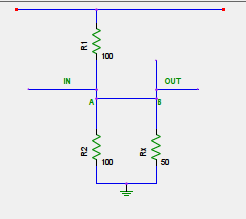


"ඉන්පුට් වෝල්ටියතාව වෝල්ට් 10 නම්, දැන් R2 හරහා වෝල්ට් 5ක් ඩ්රොප් වී ඇත" මෙතන ඉන්පුට් වෝල්ටීයතාවය කියන්නේ in වලට දෙන වෝල්ටියතාවයද? එතකොට 1:1 අනුපාතයෙන් R1 R2 බෙදෙන්නේ කොහොමද? තව පොඩි දෙයක් "එම සංඥා විදුලියද සුපුරුදු ලෙසම R1-R2 විභව බෙදුමේ 1:1 අනුපාතයට බෙදී යයි" මෙතන ටිකක් පැහැදිලි නෑ වගේ. in වලට විභවයක් දුන්නම A වල විභවයත් ඒකම නෙවෙයිද? R2 ලග Ground එකකුත් තියෙන නිසා....! ( සමාවෙන්න මෝඩ ප්රශ්නයක් ඇහුව නං...:) )
ReplyDeleteඑතන පොඩි අතපසුවීමක් තිබෙනවා වගේ... මගේ රූපයේ පොඩි අඩුවක් තිබෙනවා (ඉන් හා ඉන්පුට් වෝල්ටියතාව දෙකක් බව එතැන මා හඟවා නැහැ)... ඔබට එය වැටහී තිබෙනවා :) නැහැ... in වෝල්ටියතාව නොවෙයි වෝල්ට් 10 කියන්නේ. R1, R2 යන දෙකම දෙපස (එනම් උඩින් හා යටින්) දී තිබෙන ඩීසී වෝල්ටියතාවයි මා ඉන් අදහස් කරන්නේ. එම ඉන්පුට් වෝල්ටියතාව තමයි 1:1 අනුපාතයෙන් බෙදෙන්නේ. දැන් හරිනෙ... කෙසේ වුවත් ඉන්පුට් වෝල්ටියතාව හා ඉන් යන්න දෙකක් බව මා ඊට වාක්ය දෙක තුනකට පසුව හඟවා තිබෙනවා මෙලෙස " මේ කතා කළේ සංඥා විදුලිය ගැන නොව, ස්ථාවර ඩීසී විදුලිය ගැනයි. දැන් සිතන්න IN එකට සංඥා විදුලිය ඇතුලු කරනවා කියා."
Deleteදෙවැනි ප්රශ්නයත් හොඳ සාධාරණ එකක් :)එතැන මා විශාල වැරද්දක් කර තිබෙන බව පේනවා. එනම්, ධාරාව බෙදෙනවා කියනවා වෙනුවට විභවය බෙදෙනවා යනුවෙන් ලියා තිබෙනවා.
IN එකට දෙන ඒසී සංඥාවට R2 විතරද පේන්නේ/හමුවන්නේ? නැහැ. R1 හා R2 යන දෙකම එකවර සම්බන්ධයි. එහෙත් එම රෙසිස්ටර් 2 එම ඉන් සංඥාවට ශ්රේණිගතවද පෙන්නේ? නැහැනෙ... ශ්රේණිගතව නොවෙයි නම්, එය සමාන්තරගතයි නේද? මෙම තත්වය හමුවෙනවා මෙවැනි විභව බෙදුමක් මඟින් පොදු එමිටර් වින්යාසයට සැකසූ ට්රාන්සිස්ටර් බයස් කරන විට. එවිටත්, එම විභව බෙදුමේ රෙසිස්ටර් දෙක සමාන්තරගත ලෙසයි සලකන්නේ (ඊට අමතරව, එසේ හමුවූ සමක ප්රතිරෝධය නැවතත් ට්රාන්සිස්ටරයේ තුල පවතින බේස්-එමිටර් ඩයෝඩයේ ප්රතිරෝධ අගය සමග සමාන්තරව පවතින නිසා, නැවතත් සමක ප්රතිරෝධය ගණනය කර, අන්න එම අවසාන ප්රතිරෝධය සමග සංඥාවේ ඉන්පුට් ප්රතිරෝධය (එය පවතින්නේ සංඥාව සපයන පරිපථ කොටස තුලයි) සමග අවසාන වශයෙන් සංඥාව බෙදා ගන්නවා). අන්න එවැනි විස්තරයක් එතැනට ආදේශ කළ හැකියි. ඒ අනුව දෙවන ඡේදයෙත් තැන් කිහිපයක වෝල්ටියතාව වෙනුවට ධාරාව යනුවෙන් වෙනස් කළ යුතුව තිබෙනවා. මා එය නිවැරදි කරන්නම්.
මෙහිදී මා දෙයක් කියන්නට කැමතියි. මා ලියූ පාඩම් කිසිවක් සෝදුපත් බලා හෝ බලවා නැත. සාමාන්යයෙන් මා ඒ4 පිටු 20ක් පමණ එක දිගටම ටයිප් කරගෙන යනවා ලියන්න වාඩි වුණාම. බොහෝ දේවල් ලියන්නේ මතකයෙනි... ඊට අමතරව කරුණු වඩා සරල කරන්නට සාමාන්යයෙන් අනෙක් අය කරන්නට ඉදිරිපත් නොවන තරමේ දේවලුත් මා සිදු කරනවා (මාගේ "සුලු" භෞතික විද්යා දැනුම යොදාගෙන). ඉතිං ඉදහිට මෙවැනි අතපසුවීම් තිබීමට පුලුවන්. ඒවා 100%ක් නිදොස් වන පරිදි ලියන්නට ගියොත් මා හට එක් ලිපියක් අවසන් කරන්නට මාසයක් වත් යාවි. මා දැනට මේ කිසිම පොතක් මුද්රනය නොකර සිටින එක් හේතුවක්ද එයයි (ඒවා සෝදුපත් බලා, සියලුම රූප සටහන් මා විසින්ම සකස් කළ යුතුව තිබෙන නිසා).
ඔබ මෝඩ ප්රශ්න නොව ඇසුවේ. ඔබ පෙන්නුවේ ඔබගේ දැනුම ඉහල මට්ටමක තිබෙන බවයි. :)
ඔබ ඇසූ ප්රශ්නකාරී අවස්ථාව තිබෙන ඡේදයට පසු දෙවැනියට තිබෙන ඡේදය නොව ඊට තෙවැනි ඡේදයේ වැරැද්ද තිබුණේ (sorry)... එය වෙනස් කළා.
Deleteබොහෝම ස්තුතියි සර්,දැන් පැහැදිලියි. මේ ඔබ කරන්නේ ඉතා වටිනා කාර්යයක්.මං ඔබේ බ්ලොග් අඩවියෙන් වටිනා දේවල් රාශියක් ඉගෙන ගත්තා.(A/L Phisics වල electronic දැනුම විතරයි මට තිබ්බේ) දිගටම කරගෙන යන්න. ජය...!
Deleteසතුටුයි ඔබ ගැන... පුලුවන් තරම් ඉගෙන ගන්න. අපටත් උගන්වන්න. :)
Delete