ඉලෙක්ට්‍රොනික්ස් II (Electronics) - 8

ධාරිත්‍රක දෙකක් (හෝ කිහිපයක්) එකිනෙකට සම්බන්ධ කළ හැකි ආකාර දෙකක් තිබෙන බව ඔබ දැන් දැන සිටිය යුතුයි (මොකද ප්‍රතිරෝධක ගැන කතා කරන විට මා පැවසුවා ඕනෑම උපාංග දෙකක් සම්බන්ධ කළ හැකි ආකාර පවතින්නේ දෙකක් පමණක් බව). එනම්, ශ්‍රේණිගත හා සමාන්තරගත ලෙස. ශ්‍රේණිගත හා සමාන්තරගත සම්බන්ධතා දෙක ඉගෙනීමට පෙර, සරලව ධාරිත්‍රකයක් සාදන අයුරු දැන් බලමු.

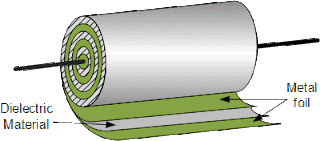
යම් සන්නායක කොටස් දෙකක් එකිනෙකට ළඟින් එහෙත් එකිනෙකට ස්පර්ශ නොවන ලෙස තැබූ විට, එතැන සෑදෙන්නේ කැපෑසිටරයකි. එම සන්නායක කොටස් දෙක තිබෙන විදිය, ඒවා කොතරම් පරතරයකින්ද තිබෙන්නේ කියන වග ආදී කරුණු කිහිපයක් මත එම කැපෑසිටරයේ ධාරිතාව තීරණය වේ. පහත රූපය බලන්න.
 

මෙම රූපය ඇසුරින් ධාරිත්‍රකයක අගය තීරණය වන සැටි ඉගෙන ගමු. සන්නායක කොටස් දෙකේ පරතරය (d) අඩුවන තරමට ධාරිතාව වැඩි වේ. දැන් තිබෙන පරතරය දෙගුණයකින් වැඩි කළ විට, ධාරිතාව භාගයකින් අඩු වේ. පරතරය දස ගුණයකින් අඩු කළ විට, ධාරිතාව දස ගුණයකින් වැඩි වේ. තවද, සන්නායක දෙකෙහි එකිනෙකට සම්මුඛව තිබෙන කොටසෙහි වර්ගඵලය (A) වැඩි වන විට, ධාරිතාව වැඩි වේ. මතක තබා ගන්න නිකංම සන්නායකයේ වර්ගඵලය වැඩිවීම නොවේ අප සලකන්නේ; උඩ හා යට තිබෙන සන්නායක දෙක එකිනෙකට කෙලින් (සම්මුඛව) තිබෙන කොටස්වල වර්ගඵලයයි සලකන්නේ. උදාහරණයක් ලෙස යට සන්නායකය මුද්දරයක තරම් විශාල නම්, ඊට උඩින් ඇති සන්නායකය පිට්ටනියක් තරම් විශාල වුවත් වැඩක් නැහැ. එතැන සත්‍ය ලෙසම සලකන්නේ අර මුද්දරය තරමේ සන්නායකයේ වර්ගඵලය පමණි. ඒ විතරක් නොවේ විශාල සන්නායක දෙකක් වුවද, ඒ දෙක තබා තිබෙන්නේ අර වහලවලට උළු (හෝ ෂීට්) යොදන ආකාරයට නම් (එනම්, උළු කැට විශාල වුවත් එක් උළු කැටයක් අනෙක් උළු කැටයක් ස්පර්ශ කරන්නේ කුඩා ප්‍රමාණයකි), එවිටද කැපෑසිටරයේ අගය සෙවීමට වර්ගඵලය ලෙස ගැනෙන්නේ එම සන්නායක දෙක එකිනෙකට සම්මුඛව (overlap) පවතින කොටසේ වර්ගඵලයයි. ඒ විතරක්ද නොවේ, කැපෑසිටන්ස් එක අඩුවැඩි වීමට තවත් සාධකයක් පවතී. එය නම් සන්නායක දෙක අතර ඇති පරිවාරකයයි. ඇත්තටම පරිවාරකයේ පාරවේද්‍යතාව (permittivity) නමින් හැඳින්වෙන ගුණයයි වැදගත්වන්නේ. පාරවේද්‍යතාව වැඩිවන තරමට ධාරිතාව වැඩි වේ. ඒ අනුව ඉහත රූපයේ ධාරිතාව මැනීමට පහත සූත්‍රය ඉතාම පහසුවෙන් අපට නිර්මාණය කළ හැකියි.

ධාරිතාව = (පරිවාරකයේ පාරවේද්‍යතාව)(සන්නායක වර්ගඵලය)/(සන්නායක දෙක අතර පරතරය)

සාමාන්‍යයෙන් ඉහත ආකාරයට සන්නායක තැටි දෙකක් පමණක් යොදාගෙන සාදාගන්නා ධාරිත්‍රකයක ධාරිතාව කුඩාය. එය වැඩි කිරීමට එවැනි “සෙට්” කිහිපයක් තබයි. එවැනි සෙට් 100ක් තැබුවේ නම්, ධාරිතාව සිය ගුණයකින් වැඩිවේ.

සටහන
සෑම ද්‍රව්‍යකටම පාරවේද්‍යතාව නම් ගුණය ඇත. ඉතා සරලවම පාරවේද්‍යතාව යනු විදුලි ක්ෂේත්‍රයක් ඇතිවීමට තිබෙන පහසුවයි. එනම්, යම් ද්‍රව්‍යයක පාරවේද්‍යතාව ඉහළ වීමෙන් කියන්නේ එම ද්‍රව්‍යය තුළ විදුලි ක්ෂේත්‍රයක් ඉතා පහසුවෙන් හා ප්‍රබලව පැවතිය හැකි බවයි. තවත් විදියකට කියන්නේ නම්, විදුලි ක්ෂේත්‍රයක් වශයෙන් වැඩිපුර (විදුලි) ශක්ති ප්‍රමාණයක් වැඩි පාරවේද්‍යතාවක් සහිත ද්‍රව්‍යයක් තුළ ගබඩා කරගත හැකියි. සෑම ද්‍රව්‍යයක් වගේම කිසිදු ද්‍රව්‍යයක් නැති රික්තකයේද පාරවේද්‍යතාවක් පවතී. අඩුම පාරවේද්‍යතාව ඇත්තේ රික්තකයටයි. එහි අගය 8.85 x 10^-12  Farads/meter වේ. අනෙක් සෑම ද්‍රව්‍යයකටම මීට වඩා වැඩි වෙනස් වෙනස් අගයන් ඇත. සාමාන්‍යයෙන් විද්‍යාව තුළ පාරවේද්‍යතාව සංඛේතාත්මකව දැක්වීමට ඉංග්‍රිසි E අකුරට තරමක් සමාන ග්‍රීක් එප්සිලෝන්, ᵋ යන අක්ෂරය යොදාගන්නවා. රික්තයේ පාරවේද්‍යතාව ᵋ₀ යන සංඛේතයෙන් දැක්වෙනවා. දළ වශයෙන් වාතයේ (වායුගෝලයේ) පාරවේද්‍යතාවද රික්තකයේ පාරවේද්‍යතාවට සමානයි. මෙම රික්තකයේ හා ද්‍රව්‍යවල පාරවේද්‍යතාව නිරපේක්ෂ පාරවේද්‍යතාව (absolute permittivity) ලෙස හැඳින්වෙනවා. ලිවීමේ, සංසන්දනය කිරීමේ, හා භාවිතයේ පහසුව පිණිස අප එක් එක් ද්‍රව්‍යයේ නිරපේක්ෂ පාරවේද්‍යතාව යොදාගන්නේ නැත. ඒ වෙනුවට සාපේක්ෂව පාරවේද්‍යතාව (relative permittivity) යොදාගන්නවා. ද්‍රව්‍යයන්ගේ සාපේක්ෂ පාරවේද්‍යතාවන් සඳහන් කරපු වගු අන්තර්ජාලයෙන් පහසුවෙන්ම සොයාගත හැකියි. සාපේක්ෂව පාරවේද්‍යතාව, ᵋ_r යනු යම් ද්‍රව්‍යක නිරපේක්ෂ පාරවේද්‍යතාව විශ්වයේ කුඩාම පාරවේද්‍යතාව අගය වන රික්තකයේ පාරවේද්‍යතාවෙන් බෙදූ විට ලැබෙන අගයයි.  

යම් ද්‍රව්‍යයක සා. පාරවේද්‍යතාව = (එම ද්‍රව්‍යයේ නි. පාරවේද්‍යතාව)/(රික්තයේ නි. පාරවේද්‍යතාව)
 
එයම සංඛේතාත්මකව ᵋ_r = ᵋ / ᵋ₀ ලෙස ලිවිය හැකියි. එවිට, යම් ද්‍රව්‍යයක නිරපේක්ෂ පාරවේද්‍යතාව ᵋ_r ᵋ₀ ලෙස ලිවිය හැකියි නේද? ඉහත සූත්‍රයේ පාරවේද්‍යතාව සඳහන් කර තිබෙන්නේ මේ අයුරින් තමයි.
  

ඉහත දැනුමත් සමග දැන් බලමු ඇත්තටම ධාරිත්‍රකයක් සාදන්නේ කෙලෙසද කියා. සෑම ධාරිත්‍රකයක්ම සාදන්නේ එකම ආකාරයටයි. එහෙත් ඊට යොදාගන්නා පරිවාරකය හා ධාරිත්‍රකයේ ප්‍රමාණය ආදිය පමණයි වෙනස්වන්නේ. සාමාන්‍යයෙන් සිදු කරන්නේ, සිහින් සන්නායක තැටි දෙකක් මැද ඉතා සිහින් පරිවාරක (dielectric) තැටියක්/සිවියක් තබා එය පහත රූපයේ ආකාරයට රෝල් කිරීමයි. ඉතා දිග තැටි මෙලෙස රෝල් කර කුඩාවට සාදා ගත හැකියි නේද? මෙලෙස රෝල් කිරීම ඉහත කියූ ලෙස “සෙට්” කිහිපයක් ලෙස සැලකිය හැකියි නේද?
 

 

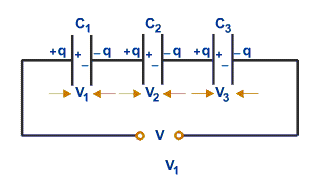
ධාරිත්‍රක දෙකක් ශ්‍රේණිගතව සම්බන්ධ කිරීම

මෙහිදී සමක ධාරිතාව අඩු වේ. සම්බන්ධ කරන ධාරිත්‍රක දෙකෙන් කුඩාම ධාරිත්‍රකයේ අගයටත් වඩා අඩු සමක ධාරිතාවක් තමයි ලැබෙන්නේ. මෙහි සමක ධාරිතාව සොයන පොදු සූත්‍රය පහත දැක්වේ.
 

1/C_T = 1/C₁ + 1/C₂ + …

මෙම ක්‍රමයෙන් සම්බන්ධ කිරීමේ ඇති වාසිය නම්, එක් එක් ධාරිත්‍රකයේ වෝල්ටියතාවන් එකතු වේ. ඒ කියන්නේ, එක් ධාරිත්‍රකයක දෙපස ඩ්‍රොප් විය හැකි උපරිම වෝල්ටියතාව වෝල්ට් 100 නම්, එවැනි ධාරිත්‍රක 10ක් ශ්‍රේණිගතව සම්බන්ධ කළ විට, වෝල්ට් 100 x 10 = 1000 ක් දැන් එම ශ්‍රේණිගත ධාරිත්‍රක පේලිය දෙපසට යෙදිය හැකියි. උදාහරණයක් ලෙස, යම් අවස්ථාවකට යෙදිය යුතු ධාරිත්‍රකය වෝල්ට් 1000ක් විය යුතු වුවත්, තමන් සතුව තිබෙන්නේ වෝල්ට් 500ක ධාරිත්‍රක නම්, මෙවැනි ධාරිත්‍රක දෙකක් ශ්‍රේණිගතව යෙදිය හැකියි නේද? එහෙත් මතක තබා ගන්න ධාරිත්‍රක ශ්‍රේණිගතව සම්බන්ධ කිරීමේදී සමක ප්‍රතිරෝධය අඩුවන බව. එමනිසා ඉහත උදාහරණයේදී ඔබට වෝල්ට් 1000ක් සපෝට් කරන 1u කැප් එකක් අවශ්‍ය කරනවා යැයි සිතමු. එහෙත් ඔබ සතුව වෝල්ට් 1000ක් සපෝට් කරන කැප් නැත; ඒ වෙනුවට වෝල්ට් 500ක් සපෝට් කරන කැප් ඇත. ඉතිං අපට අවශ්‍ය කරන්නේ 1u අගයකි. ඒ කියන්නේ 500v, 2u කැප් දෙකක් ශ්‍රේණිගතව සම්බන්ධ කිරීම නේද කළ යුත්තේ? එහෙම නැතිනම්, වෝල්ට් 100හේ 10u කැප් දහයක් ශ්‍රේණිගතව සම්බන්ධ කරන්නත් පුලුවන්.
 

එහෙත් මෙහි ඇති එක් භයානක කමක් තිබේ. සිතන්න ඉහත කියූ ලෙසට අධික භාහිර වෝල්ටියතාවකට සපෝට් කිරීම පිණිස සුදුසු අගයන්ගෙන් යුතු ධාරිත්‍රක කිහිපයක් ශ්‍රේණිගතව සම්බන්ධ කළා කියලා. දැන් කිසියම් හේතුවක් නිසා, මින් එක් ධාරිත්‍රකයක් ෂෝට් වූයේ නම් (ඒ කියන්නේ ධාරිත්‍රකය දැන් නිකංම වයර් කැබැල්ලක් සේ ක්‍රියා කරනවා), එම භාහිර වෝල්ටියතාව දැන් පිහිටන්නේ ඉතිරි කැපෑසිටර් දෙපසයි. එවිට, එම වෝල්ටියතාව ඒවා සපෝට් කරන උපරිම වෝල්ටියතාව ඉක්මවා යෑම නිසා, අනෙක් කැපෑසිටර්ද පිලිස්සී යනවා. ඉහත උදාහරණයම ගතහොත්, කැපෑසිටර් දහයෙන් එකක් ෂෝට් වූ විට, භාහිර 1000 වෝල්ටියතාව දැන් ඉතිරි කැපෑසිටර් 9 අතරේ බෙදේ. එවිට, එක් ධාරිත්‍රකයකට වෝල්ට් (1000/9=) 111ක් පමණ ලැබේ (වැඩිපුර වෝල්ට් (111-100=) 11ක්). එහෙත් එම උදාහරණයේ එක් කැපෑසිටරයකට උපරිමව දැරිය හැක්කේ වෝල්ට් 100ක් පමණි. ඒ කියන්නේ ඉතා ඉක්මනින් තවත් කැපෑසිටරයක් හෝ කිහිපයක් පිලිස්සී යනවා. එවිට ප්‍රශ්නය තවත් බරපතල වී ක්ෂණයකින් සියලුම කැපෑසිටර් පිලිස්සී යාවි. මීට යම් පිළියමක් ලෙස, එක් එක් ධාරිත්‍රකයේ උපරිම වෝල්ටියතා අගයෙන් 75% ක් හෝ 50% ක් එහි වෝල්ටියතාව ලෙස සලකා ගණනය කිරීම් කළ හැකියි. ඉහත උදාහරණයම ගතහොත්, එක් එක් ධාරිත්‍රකයක් වෝල්ට් 100ක් දැරිය හැකි වුවත්, එය වෝල්ට් 50ක් දැරිය හැක්කේ යැයි උපකල්පනය කරන්න. එවිට, දැන් භාහිර වෝල්ටියතාව වන වෝල්ට් 1000 ට සමාන වීමට ධාරිත්‍රක 20ක් (10ක් නොවේ) ශ්‍රේණිගතව යෙදිය යුතු වෙනවා. මෙවිට එක් ධාරිත්‍රකයක් ෂෝට් වූවිට, එම වැඩිවන වෝල්ට් ගණන පෙර අවස්ථාවට වඩා අඩුය (පෙර වෝල්ට් 100 වෙනස වෙනුවට දැන් ඇතිවන්නේ වෝල්ට් 50ක වෙනසකි). ඒ විතරක් නොවේ, එම කුඩා වෙනස දැන් ධාරිත්‍රක විශාල ප්‍රමාණයක් අතරේ බෙදී යන නිසා, එක් එක් ධාරිත්‍රකයට අමතරව වැඩිවන ප්‍රමාණයද පෙරට වඩා අඩු වේ (වැඩිපුර වෝල්ට් (50/19=) 2.5ක්). ඒ විතරක්ද නොවේ, එසේ අමතරව වැඩි වන වෝල්ටියතා ප්‍රමාණය කිසි ප්‍රශ්නයක් නැතිව දැරිය හැකිද වේ (මක්නිසාද වෝල්ට් 50 ලෙස ගත්තත්, සැබෑ ලෙසම ඒවාට වෝල්ට් 100ක් දක්වා දැරිය හැකි නිසා). ඒ අනුව එක් ධාරිත්‍රකයක් ෂෝට් වීම නිසා ඉතිරි අනෙක් ධාරිත්‍රකයකට ඉහත අමතරව දැරීමට සිදුවන වෝල්ට් 2.5 සමගම සම්පූර්ණයෙන් වෝල්ට් 52.5ක් දැරීමට සිදු වේ. ඉන් කිසිදු ප්‍රශ්නයක් නැහැ නේද මොකද සත්‍ය ලෙසම එක් ධාරිත්‍රකයකට වෝල්ට් 100ක උපරිම අගයක් දක්වා දැරිය හැකි නිසා.
 

ඉහත සූත්‍රය බැලූවිට සිහිපත් වන්නේ ප්‍රතිරෝධක දෙකක් සමාන්තරගතව සම්බන්ධ කරනවිට යෙදිය යුතු සූත්‍රය නේද? ඉහත සූත්‍රය සාධනය (proof) කරන්නේ කෙසේද? ඉහත රූපය බලන්න. එහි ධාරිත්‍රක ශ්‍රේණිගතව ඇත. මීට සුපුරුදු ලෙස KVL දමන්න. එවිට, එක් එක් ධාරිත්‍රකය දෙපස ඩ්‍රොප් වන වෝල්ටියතාවල මුලු එකතුව භාහිරින් සපයා ඇති වෝල්ටියතාවට සමාන වේ. එක් එක් ධාරිත්‍රකය සඳහා Q=CV යන සූත්‍රය දැන් යොදන්න. මෙහිදී සෑම ප්‍රතිරෝධකයකම ගබඩාවන ආරෝපණ (ඉලෙක්ට්‍රෝන) ප්‍රමාණය සමාන ලෙස සැලකිය යුතුය. ඒ ඇයි? මෙහෙම සිතන්න. දකුණු කෙළවරම ඇති කැපෑසිටරයේ දකුණු තහඩුවට බැටරියෙන් ඉලෙක්ට්‍රෝන පැමිණේ. එම ඉලෙක්ට්‍රෝනවලට සමාන ප්‍රමාණයක් එහි වම් තහඩුවෙන් ඉවත්ව යයි. දැන් එම වම් තහඩුව සම්බන්ධ කර තිබෙන්නේ දෙවැනි කැපෑසිටරයේ දකුණු තහඩුවටයි. ඉතිං එම ඉලෙක්ට්‍රෝන සියල්ල දෙවැනි ධාරිත්‍රකයේ දකුණු තහඩුව මත රැස්වේ. එවිට දෙවැනි ධාරිත්‍රකයේ වම් තහඩුවෙන් එවැනිම ඉලෙක්ට්‍රෝන ප්‍රමාණයක් විකර්ෂණය වී ගොස් තෙවැනි කැපෑසිටරයේ දකුණු තහඩුව මත රැස්වේ. මේ ආදී ලෙස පිළිවෙලින් ඉලෙක්ට්‍රෝන කැපෑසිටරයෙන් කැපෑසිටරයට ගමන් කරයි. අවසානයේ වම් කෙළවර ඇති කැපෑසිටරයේ වම් තහඩුවෙන් ඉලෙක්ට්‍රෝන ඉවත්ව බැටරියට ඇතුලු වේ. මේ සෑම තැනකදීම කැපෑසිටරයෙන් කැපෑසිටරයට ගමන් කළේ එකම ඉලෙක්ට්‍රෝන ප්‍රමාණයක් හෙවත් එකම ආරෝපණ ප්‍රමාණයක් නේද? එනිසයි සෑම ධාරිත්‍රකයම ගබඩාවන්නේ එකම ආරෝපණ ප්‍රමාණයක් කියා පැවසුවේ. ඒ අනුව,
 

V_T = V₁ + V₂ + V₃ + …
(Q=CV → V=Q/C) යෙදීමෙන්, Q/C_T = Q/C₁ + Q/C₂ + Q/C₃ + …
1/CT = 1/C₁ + 1/C₂ + 1/C₃ + …
 

ප්‍රතිරෝධකවල සේම, මෙහිදීද 10% රීතිය යෙදිය හැකියි. එම අවස්ථාවේ සඳහන් කරපු සියලු විස්තර මෙහිදීද වලංගු වේ.
 

ධාරිත්‍රක දෙකක් සමාන්තරගතව සම්බන්ධ කිරීම

මෙහිදී සමක ධාරිතාව වැඩි වේ. එනම්, සම්බන්ධ කරන ධාරිත්‍රක දෙකෙහි වැඩිම අගයටත් වඩා සමක අගය වැඩිය. මෙහිදී ගබඩාවන මුලු ශක්තිය කැපෑසිටර් සියල්ලෙහිම තනි තනි ශක්තිවල එකතුව වේ. ඒ කියන්නේ මේ ආකාරයට කැපෑසිටර් සම්බන්ධ කරන විට, ගබඩාවන ශක්තිය වැඩි වේ. සමාන්තරගතව සම්බන්ධ කරන හැම ධාරිත්‍රකයක්ම එකම වෝල්ටියතාවෙන් තැබීම උචිතය. එක් එක් වෝල්ටියතාවන් සහිත ධාරිත්‍රක සම්බන්ධ කර ඇති විට, ඒ අතරින් අඩුම වෝල්ටියතාව සහිත ධාරිත්‍රකය තමයි මුල් තැන ගන්නේ (ඒ කියන්නේ අනෙක් වැඩි වෝල්ටියතා ධාරිත්‍රකවලත් සත්‍ය ලෙස භාවිතා කළ හැකි වෝල්ටියතාවන් පහළම ධාරිත්‍රකයේ වෝල්ටියතා මට්ටමට වැටේ). එය ගණනය කරන සූත්‍රය පහත දැක්වේ.
 

C_T = C₁ + C₂ + …
 

එය බැලූබැල්මට ශ්‍රේණිගතව සම්බන්ධ කළ ප්‍රතිරෝධකවල සමක අගය සොයන සූත්‍රය වැනියි නේද?එම සූත්‍රයද පහත ආකාරයට සාධනය කළ හැකියි. ඉහත රූපය බලන්න. එහි ධාරිත්‍රකවල දෙපස ඩ්‍රොප් වන වෝල්ටියතා සියල්ල සමාන වන අතර, එම අගය භාහිර වෝල්ටියතාවේ අගයටද සමාන වේ. ඒ වගේමයි, දැන් එක් එක් ධාරිත්‍රකයට වෙන වෙනම භාහිර බැටරියෙන් ආරෝපණ ස්වාධීනව ලැබේ. ඒ කියන්නේ පෙර අවස්ථාවේ මෙන්, එක් ධාරිත්‍රකයෙන් පිටවන ආරෝපණ අනෙක් ධාරිත්‍රකයට ගමන් නොකර කෙලින්ම බැටරිය සමග ගනුදෙනු කරයි. මෙවිට, එක් එක් කැපෑසිටරයේ තිබිය හැකි ආරෝපණ ප්‍රමාණය වෙනස් විය හැකියි. ඒ විතරක්ද නොවේ, එම ධාරිත්‍රක සියල්ලේම ආරෝපණවල එකතුව බැටරියෙන් පිටකරන මුලු ආරෝපණ ප්‍රමාණයට සමානද විය යුතුය. ඊට නැවතත් Q=CV සූත්‍රය යෙදිය හැකියි. ඒ අනුව,
 

Q_T = Q₁ + Q₂ + Q₃ + …
(Q = CV යෙදීමෙන්) C_TV = C₁V + C₂V + C₃V + …
C_T = C₁ + C₂ + C₃ + ...

 

ධාරිත්‍රක අගය සෙවීම

දැන් බලමු ධාරිත්‍රකයක අගය සොයන අයුරු. අාකාර කිහිපයක් ඇත. සමහර ධාරිත්‍රක මත එහි අගය පැහැදිලිවම ලියා දැක්වේ. පහත රූපය බලන්න. කැපෑසිටරයක කැපෑසිටන්ස් එකට අමතරව, එයට යෙදිය හැකි උපරිම වෝල්ටියතාවද දක්වනවා. මේවායේ අමුතුවෙන් අගයන් සෙවීමේ ක්‍රම නැත. පිකෝෆැරඩ්වලින් අගයන් දක්වන විට අගයට පිටුපස p අකුර සටහන් කෙරේ. එලෙසම නැනෝෆැරඩ් දැක්වීමට n ද, මයික්‍රොෆැරඩ් දැක්වීමට u ද සටහන් කෙරේ. දශම අගයන් සටහන් කරන විට, දශම තිත වෙනුවට ඉහත අකුරක් එතැනට යෙදිය හැකියි. උදාහරණයක් ලෙස, 4.7u යන්න 4u7 ලෙස ලියයි.

තවත් වර්ග සඳහා, ප්‍රතිරෝධකවලට තිබුණා මෙන් කලර් කෝඩ් ක්‍රමයක් අනුගමනය කළ යුතු වෙනවා. එහි වර්ණවලට හිමි අගයන් ප්‍රතිරෝධකවල දක්නට ලැබුණු ඒවාම වේ. සාමාන්‍යයෙන් වර්ණ තීරු 5ක් ඇත. ඉන් පළමු වර්ණ තීරුවෙන් දැක්වෙන්නේ ධාරිත්‍රකයේ උෂ්ණත්ව සංගුණක අගයයි. එම වර්ණ තීරුව තරමක් කෙළවරට වෙන්නට තිබෙන නිසා පහසුවෙන්ම එය හඳුනාගත හැකියි. සමහරවිට, එම තීරුව අනෙක් තීරුවලට වඩා මහතට තිබේ. හොඳින් මතක තබා ගන්න ප්‍රතිරෝධකවල අගයන්ට පමණක් නොවේ උෂ්ණත්ව සංගුණකයක් තිබෙන්නේ. දැන් සාකච්ඡා කරන ධාරිත්‍රකවල අගයන්ට, පසුවට කතා කරන වෙනත් ඕනෑම උපාංගයක අගයන්ටද උෂ්ණත්ව සංගුණක පවතිනවා, මක්නිසාද උෂ්ණත්වය අනුව උපාංගවල අගයන් වෙනස් වෙනවා. ප්‍රතිරෝධක පාඩමේදී උෂ්ණත්ව සංගුණක ගැන කියූ විස්තර එලෙසම මෙම අවස්ථාවන්ටද අදාල වේ. බොහෝවිට ඍණ තාප සංගුණක අගයක් තමයි ධාරිත්‍රක සඳහා තිබෙන්නේ. දෙවන, තෙවන, හා සිව්වැනි වර්ණ තීරුවලින් දැක්වෙන්නේ ධාරිත්‍රකයේ ධාරිතාවයි. එම අගය ලැබෙන්නේ පිකෝෆැරඩ්වලින්ය. මෙහිදී දෙවන හා තෙවැනි ඉලක්කම් එලෙසම ලියා සිව්වන ඉලක්කමට සමාන බිංදු ගණනක් ලිවීමයි කරන්නේ (සුපුරුදු ලෙසම). එහෙත් ගුණාකාරය හඟවන සිව්වැනි වර්ණයට හිමි ඉලක්කම 8 නම්, එවිට ඊට සමාන බිංදු ගණනක් නොදමා, ඊට පෙර තිබූ වර්ණවලින් ලැබුණු අගය 0.01න් ගුණ කරන්න. එලෙසම, ගුණාකාර වර්ණයට හිමි ඉලක්කම 9 නම්, එහිදීද බිංදු 9ක් නොදමා ඒ වෙනුවට 0.1න් ගුණ කරන්න.
 

අවසන් වර්ණ තීරුවෙන් කියන්නේ සහනතා/ටොලරන්ස් අගයයි. සහනතා ප්‍රතිශතය ගැනද මීට පෙර ප්‍රතිරෝධක පැහැදිලි කරන අවස්ථාවේ සඳහන් කරපු විස්තර එලෙසම අදාළ වේ. පහත රූපයේ (වගුවේ) පෙනෙන පරිදි සහනතා අගය තීරු දෙකක් තිබේ. පිකෝෆැරඩ් 10ට වැඩි ධාරිත්‍රක සඳහා ප්‍රතිශත වශයෙන් ඇති සහනතා තීරුව වලංගු වන අතර, පිකෝෆැරඩ් 10 ට අඩු ධාරිත්‍රක සඳහා නිශ්චිත අගයන් සහිත සහනතා තීරුවද වලංගු වේ.
 

තවද, ධාරිත්‍රකය මත වර්ණ සටහන් කිරීමේදී ආකාර කිහිපයක් තිබේ. වර්ණ තීරු (bands) ලෙස හෝ වර්ණ තිත් (dots) ලෙස හෝ ඒවා සටහන් කර තිබිය හැකියි. විවිධ හැඩවලින් යුතුව ධාරිත්‍රක සාදා තිබෙන අතර, ඒ ඒ හැඩයන් සඳහා වර්ණ සටහන් කර තිබෙන අයුරු පහත රූපයේ දැක්වේ. සාමාන්‍ය වර්ණ පහ වෙනුවට වර්ණ තුනක් සහිත ධාරිත්‍රකත් තිබේ. එවිට තාප සංගුණකය හා සහනතා අගය හඟවන වර්ණ එහි සටහන් කරන්නේ නැත. පහත රූප හොඳින් අධ්‍යනය කර වර්ණ තීරු වටහ ගන්නා අයුරු ඉගෙන ගන්න. (තවත් අවස්ථාවල, කැපෑසිටරයේ පළමු වර්ණ තීරු තුනෙක් එහි කැපෑසිටන්ස් එකද, සිව්වැනි වර්ණයෙන් ටොලරන්ස් එකද, පස්වැනඅ වර්ණයෙන් තාප සංගුණකයද දකවනවා.)
 

ධාරිත්‍රකවල අගය සොයන තවත් ක්‍රමයක් නම් ඉලක්කම් තුනක් හා ඉංග්‍රිසි අකුරක් සහිත කේත ක්‍රමයයි. මෙහිදී පළමු ඉලක්කම් දෙක එලෙසම ලියා, තෙවැනි ඉලක්කමට සමාන බිංදු ගණනක් දමන්න. මෙහිදී විශේෂයෙන් දෙයක් කිව යුතුය (වර්ණ තීරු විස්තරයේදිත් මේ ගැන කතා කළා). එනම්, රෙසිස්ටර්වල මෙන් නොව, කැපෑසිටර්වල ගුණාකාරය හඟවන (තුන්වැනි) ඉලක්කමට තිබෙන අගය 8 නම්, එවිට බිංදු 8ක් නොදමා, ඒ වෙනුවට මුල් ඉලක්කම් දෙකෙන් දැක්වෙන අගය 0.01න් වැඩි කරන්න. එලෙසම, එම ඉලක්කම 9 නම්, මුල් ඉලක්කම් දෙකෙන් දැක්වෙන අගය 0.1න් වැඩි කරන්න. එවිට ලැබෙන අගය පිකෝෆැරඩ්වලින් වේ. අවසන් ඉංග්‍රිසි අකුරින් කියන්නේ සහනතා අගයයි. පහත රූපය අධ්‍යනය කරන්න. එම “ඉලක්කම් තුනේ හා තනි ඉංග්‍රිසි අකුරේ කෝඩ් එක” හෙවත් ඇල්ෆනියුමරික් කෝඩ් එකට අමතරව තවත් කුඩා කෝඩ් එකක් සමහර කැපෑසිටර් මත ලියා තිබෙනවා. (132 වැනි ඉලක්කම්වලින් පමණක් දැක්වෙන කෝඩ් numeric code ලෙසද, XYS වැනි ඉංග්‍රිසි අකුරුවලින් පමණක් දැක්වෙන කෝඩ් letter/alphabetic code ලෙසද, 132F වැනි ඉලක්කම් හා අකුරු දෙකම කලවම්ව පවතින විට alphanumeric code ලෙසද කෝඩ් නම් කෙරෙනවා.) එයින් කියන්නේ උපරිම වෝල්ටියතාවයි. සමහර කැපෑසිටර් වෝල්ටියතාව දැක්වීමට එවැනි කෝඩ් එකක් භාවිතා කරන අතර, සමහර කැපෑසිටර් කෙලින්ම වෝල්ටියතාව සඳහන් කරනවා. පහත එම වගු සියල්ල දැක්වේ. පිකෝ, නැනෝ, මයික්‍රො යන ඒවා හැඟවීමට ධාරිතාව අගට යොදන p, n, u ආදී අකුරු කෝඩ්වල අකුරු නොවන බව මතක තබා ගන්න. ඒවා නිකංම රාශියක අගය පෙන්වන අකුරු හෝ දහයේ විවිධ ගුණාකාර හැඟවීමට යොදන අකුරු පමණි.
 

මීට අමතරව, තවත් ධාරිත්‍රකවල අගය සටහන් කර තිබෙන්නේ ඉහත කිසිම ක්‍රමයකට අනුගත නොවන කුමක් හෝ කෝඩ් එකකිනි. විශේෂයෙන් SMD වර්ගයේ කැපෑසිටර්වල මෙම ක්‍රමය භාවිතා විය හැකියි. එවැනි අවස්ථාවලදී, සුදුසු ටේබල් එකක් (වගුවක්) භාවිතා කරගෙන එම කෝඩ් එකට ගැලපෙන අගය සොයා ගත හැකියි. ඇත්තමට මෙම ක්‍රමය නම් තරමක් කරදරකාරියි මක්නිසාදයත් එක් එක් නිෂ්පාදකයා විවිධ කෝඩ් හා වගු ඉදිරිපත් කර තිබෙනවා. සමහරවිට එක් නිෂ්පාදකයෙක් සාදපු එවැනි කැපෑසිටරයක ඇති කෝඩ් එකක් තවත් නිෂ්පාදකයෙක්ද යොදාගන්නට පුලුවන්. එහෙත් ඔවුන් භාවිතා කරන වගු වෙනස් නිසා, කෝඩ් එක සමාන වුවත්, සත්‍ය ධාරිතා අගයන් වෙනස් විය හැකියි. එනිසා, ඔබ සතුව ඇති කැපෑසිටරය නිපදවා ඇති නිෂ්පාදකයාගේ නිවැරදි වගු භාවිතා කරන්න හැමවිටම. (ඇත්තටම මෙම තත්වය කැපෑසිටර්වලට පමණක් නොවේ, රෙසිස්ටර්, ඉන්ඩක්ටර්, ඩයෝඩ්, ට්‍රාන්සිස්ටර් ආදී අනෙකුත් උපාංග සඳහාද පොදුය; විශේෂයෙන් එම උපාංග SMD ආකාරයෙන් පවතින විට.)
 

ධාරිත්‍රකද සෑම අගයක් සඳහාම නිපදවා නැත. රෙසිස්ටර් සාදපු ක්‍රමයටම යම් ශ්‍රේණි ලෙස ඒවායේ අගයන් නිපදවා තිබෙනවා. රෙසිස්ටර්වල භාවිතා කළ E12 ශ්‍රේණියම බහුල වශයෙන් කැපෑසිටර් සඳහාද යොදාගන්නවා. මේවායේ සහනතා අගය 10% වේ. මීට අමතරව 20% සහනතා ප්‍රතිශතයක් සහිත E6 ශ්‍රේණිය හා 5% සහනතා ප්‍රතිශතයක් සහිත E24 ශ්‍රේණියද භාවිතා වේ. මීට අමතරව සමහර නිෂ්පාදකයන් ඉහත ශ්‍රේණිවලට අනුගත නොවන අගයන් සහිතවද ධාරිත්‍රක නිපදවනවා.
 

ධාරිත්‍රක ගැන පොදුවේ අනුගමනය කළ යුතු රීතියක් තිබෙනවා. ඔබ දන්නවා සෑම ධාරිත්‍රකයකටම දැරිය හැකි උපරිම වෝල්ටියතාවක් පවතිනවා. එහෙත් කිසිවිටක එම උපරිම වෝල්ටියතාව දෙන්න එපා. සිරිතක් වශයෙන් ඔබට අවශ්‍ය වෝල්ටියතාව මෙන් දෙගුණයක වෝල්ටියතාවක් සහිත ධාරිත්‍රකයක් යොදන්න. ඔබ උපකරණ අලුත්වැඩියා කරන විටත් මතක තබා ගත යුතු දෙයක් තිබේ. තිබෙන කැප් එකක් ඉවත් කර අලුත් එකක් යොදන විට, එම ඉවත් කරන කැප් එකේ වෝල්ට් ගණනට සමාන හෝ ඊට වඩා වැඩි වෝල්ටියතාවක් සහිත කැප් එකක් හැමවිටම යොදන්න. ඇත්තටම යොදන කැප් එකේ වෝල්ට් ගණන වැඩි වූවාට ගැටලුවක් නැත (ටිකක් මිල නම් වැඩි වේවි). එහෙත් අඩු වෝල්ට් ගණනක් සහිත කැප් එකක් යොදන්න නම් එපා. අනිවාර්යෙන්ම එය පිලිස්සී යනවා.

ඉලෙක්ට්‍රෝනික්ස් (electronics) ...