සරල ඩයිපෝල් ඇන්ටනා සෑදීම
ඩයිපෝල්
ඇන්ටනාවක හැමවිටම සරල සන්නායක
බට/වයර්
දෙකක් තිබෙනවා. මෙම
බට දෙක අතර පරතරය ඇන්ටනාවෙන්
ග්රහණය කරන්නට බලාපොරොත්තු
වන මූලික තරංග ආයාමයට සාපේක්ෂව
ඉතා කුඩා විය යුතුය.
බට දෙකට
ට්රාන්ස්මීටරයේ සිට එන සංඥා
ෆීඩ්ලයින් එක හරහා ඇතුලු
කරන්නේ මැදින් වේ. මෙම
බට දෙකෙහි දිග සාමාන්යයෙන්
එක සමාන වන අතර, එම
දිග වෙනස් වනවා එය සපෝට් කරන
සංඥා සංඛ්යාතය අනුව.
බට දෙකෙහිම
දිග හෙවත් එක බටයක දිග මෙන්
දෙගුණය dipole length (ඩයිපෝලයේ
දිග) ලෙස
හැඳින්වේ.
මෙම
ඩයිපෝල් දිග දළ වශයෙන් සංඥා
තරංග ආයාමයෙන් ½ ක්
වන විට එය resonant antenna එකකි;
මෙවිට ඩයිපෝල්
දිග (එනම්
λ/2)
resonant length
හෝ
half-wavelengthලෙස
හැඳින්වේ.
ඒ ආකාරයට
සාදන ඇන්ටනා half-wavelength
antenna ලෙස
හැඳින්වේ.
ප්රායෝගික
සම්මත ඇන්ටනාව මෙය වන අතර,
අනෙක්
ඇන්ටනා මීට සාපේක්ෂව සලකා
බැලේ.
රිසෝනන්ට්
ලෙන්ත් එකට වඩා ඩයිපෝල් දිග
අඩු වුවොත් එය electrically
short/small antenna ලෙස
හැඳින්වේ. ඇත්තටම
ඩයිපෝල් දිග තරංග ආයාමයෙන්
1/10 ක්
(λ/10)
හෝ ඊට වඩා
අඩු විය යුතුයි ෂෝට් ඇන්ටෙනාවක්
වීමට නම් (අප
මෙම සම්මතය පිලිගමු).
තවත් සමහරෙක්ට
අනුව ෂෝට් ඇන්ටෙනාවක් වීමට
ඩයිපෝල් දිග λ/π
හෙවත්
λ/3.14
හෝ ඊට වඩා
කුඩා විය යුතුයි.
එලෙසම
ඩයිපෝල් දිග තරංග ආයාමයෙන්
½ කට
වඩා වැඩි වුවොත් එය electrically
long antenna ලෙස
හැඳින්වේ.
ඉතා
දිගු තරංග ආයාම සහිත රේඩියෝ
තරංග විසුරුවා හැරීමේදී හා
ග්රහණය කිරීමේදී ප්රායෝගික
ගැටලු ඇති වේ.
එනම්,
ඉතා විශාල
ඩයිපෝල් දිගවල් (මීටර්
සිය ගණන් හෝ දහස් ගණන්)
භාවිතා
කිරීමට සිදු වේ.
එය කළ
නොහැකියිනෙ.
උදාහරණයක්
ලෙස සාමාන්ය AM
radio සඳහා
මීටර් 150ක්
වත් දිග ඩයිපෝල් දිගක් අවශ්ය
වේ (300,000,000ms-1/1,000,000Hz
= 300m → 300/2=150m). එහෙත්
මෙතරම් දිග ඇන්ටනාවක් ඔබේ
රේඩියෝ යන්ත්රයට සවි කරන්නේ
නැහැ. ඒඑම්
රේඩියෝවක ඇති ඒරියල් එක
(ඇන්ටනාව)
අඩුම ගානේ
මීටරයක් තරම්වත් දිග නැහැ
නේද? ඒ
කියන්නේ අප දැන් භාවිතා කරන්නේ
ඉලෙක්ට්රිකලි ෂෝට් ඇන්ටනාවකි.
එහෙත්
ඒඑම් සංඥා විසුරුවා හරින විට
ඉතා විශාල/උස
ටවර් ගසා ඉලෙක්ට්රිකලි ෂෝට්
නොවන සාමාන්ය ඇන්ටනාවකින්
එය විසුරුවා හැරිය හැකියි.
මේ ආකාරයට
ඉතා කුඩා රේඩියෝ යන්ත්ර
අවසංඛ්යාත සංඥා භාවිතා කරන
විට සාමාන්යයෙන් භාවිතා
කරන්නේ ඉලෙක්ට්රිකලි ෂෝට්
ඇන්ටනා තමයි.
එනිසා
දැන් මෙම ඇන්ටනා ගැන මඳක්
විමසා බලමු.
සටහන
Electrical
Length
ෆීඩ්ලයින්
එකක් හෝ සංඥා ගමන් කරන වෙනත්
වයරයක් හෝ ගත් විට,
එහි දිග
ගැන අපට කතා කරන්නට සිදු
වෙනවානෙ.
අඩි හෝ
මීටර් හෝ වෙනත් ඒකකයකින් එම
දිග දැක්විය හැකියි.
එම දිග
physical length
වේ.
එහෙත්
මෙහිදී ප්රායෝගික අපහසුතා
ඇති වන අවස්ථා කිහිපයක් මතු
වේ. එනිසා
electrical
length කියා
සංකල්පයක් හඳුන්වා දී ඇත.
මෙහිදිත්
අවසාන වශයෙන් මීටර්,
අඩි ආදි
ඒකකයෙන් මැනගත හැකි දිගක්
ලැබූණත්,
විදුලිමය
වශයෙන් වෙනත් වැදගත්කමක්
ඉලෙක්ට්රිකල් ලෙන්ත් වලට
ඇත. එනිසා
සාමාන්ය ෆිසිකල් ලෙන්ත් හා
ඉලෙක්ට්රිකල් ලෙන්ත් අතර
දිගෙහි වෙනසක් හැමවිටම ඇත.
ඒ ගැන
කෙටියෙන් බලමු.
ඇත්තටම යම්
සන්නායකයක ඉලෙක්ට්රිකල්
ලෙන්ත් යනු ඒ හරහා ගමන් කරන
සංඥා විදුලියට සත්ය ලෙස දැනෙන
දිග යැයි කිව හැකිය.
එලෙස අපට
වෙනස් විදියටත් විදුලියට
වෙනස් විදියටත් සන්නායක දිගක්
දැනෙන්නට හේතු තිබේද?
ඔව්.
සාමාන්යයෙන්
පවතින තත්වයට වඩා විශේෂිත
කරුණු බලපෑම නිසා සමහර භෞතික
පරිසරයන් වෙනස් වේ.
ඉතිං අප
එම නව භෞතික තත්වයන් නොසලකා
හැර සාමාන්ය තත්ව යටතේ සිතුවොත්
තමයි ෆිසිකල් ලෙන්ත් හමු
වන්නේ.
අර අලුත්
තත්ව යටතේ සිතුවොත් ඉලෙක්ට්රිකල්
ලෙන්ත් ලැබේ.
ඉතිං අප
යම් තත්වයක් සැලකිල්ලට නොගැනීම
අපේ දුර්වලකමක් මිස වයර්වලට
එය දැනීම අරුමයක් නොවෙයි නේද?
උදාහරණයකින්ම
ඉහත වෙනස වටහා ගමු.
සිතමු
අපට අවශ්ය යැයි කියා මෙගාහර්ට්ස්
100ක
සංඥාවක් ගමන් කරවීමට එහි තරංග
ආයාමයෙන් ¼
ක ෆීඩ්ලයින්
එකක් (කොඇක්සියල්
කේබල් කෑල්ලක්).
මෙවිට
අප සාමාන්යයෙන් c=fλ
යන සූත්රය
අනුව පළමුව තරංග ආයාමය සොයා
ගෙන ඉන් කාලක දිගක් සොයා ගන්නවා.
මෙවිට
එකවර අපට සිතෙන්නේ වයරයක්
තුලින් විදුලි සංඥා (ඉතාම
ආසන්න වශයෙන්)
ආලෝකයේ
වේගයට සමාන බවයි.
ඒ අනුව
ඉහත සංඥාවේ තරංග ආයාමය වන්නේ
300,000,000/100,000,000
= 3 meter වේ.
ඉන් කාලක්
මීටර් 0.75
හෙවත්
සෙන්ටිමීටර් 75කි.
මෙම දුර
ෆිසිකල් ලෙන්ත් වේ.
එහෙත් ඉහතදී
අප විසින් නොසලකා හැරපු නව
සාධකයක්/තත්වයක්
තිබේ. එනම්
සම්ප්රේෂන රැහැනක් ඔස්සේ
සංඥා යන විට,
ආලෝකයේ
වේගයට වඩා අඩු වේගයකිනුයි එම
සංඥා ගමන් කරන්නේ.
සත්ය
වේගය ආලෝකයේ වේගයෙන් බෙදූ
විට ලැබෙන අනුපාත අගයට එම
කේබලයේ velocity
factor (VF) යැයි
කියනවා.
උදාහරණයක්
ලෙස ඉහත ගත් කොඇක්සියල් කේබලයේ
වෙලෝසිටි ෆැක්ටර් අගය 0.66
යැයි
සිතමු. ඒ
කියන්නේ අලෝකයේ වේගය මෙන්
0.66ක
(හෙවත්
1/3 ක)
සංඥා
වේගයක් එහි ඇත.
මෙවිට
කේබලය දිගේ සංඥාවේ වේගය
300,000,000 x 0.66
= 200,000,000ms-1 වේ.
දැන් c=fλ
යන
සූත්රයට දැමිය යුත්තේ මෙම
වේගය වන අතර,
එවිට
තරංග ආයාමය ලෙස 200,000,000/100,000,000
= මීටර්
2
ලැබේ.
ඉන්
කාලක් ගත් විට මීටර් 0.5ක්
හෙවත් සෙන්ටිමීටර් 50ක්
ලැබේ.
ඉහත දෙවනුව
ලැබූ දිග ඉලෙක්ට්රිකල් ලෙන්ත්
වේ. දැන්
බලන්න මෙම ඉලෙක්ට්රිකල්
ලෙන්ත් අගය ෆිසිකල් ලෙන්ත්
අගයට වඩා අඩුයි.
ඉතිං,
අප ප්රායෝගික
ගණනය කිරීම්වලදී භාවිතා කළ
යුත්තේ ඉලෙක්ට්රිකල් ලෙන්ත්
අගය වේ.
ඇත්තටම ඉහත
තේරුමට අමතරව ඇන්ටනාවලදී
electrical length
යන්නට
වෙනත් තේරුමක්ද ඇත.
යම්
ඇන්ටනාවක් (ඩයිපෝලයක්)
අනුනාදී
වන්නේ එක් නිශ්චිත සංඛ්යාතයකටනෙ.
ඇන්ටනාවක්
අනුනාදී අවස්ථාවේදී එහි
ප්රතිබාද අගය ශූන්ය වී
ප්රතිරෝධය පමණක් ඉතිරි වේ.
එහෙත්
එම ඇන්ටනාවම එය අනුනාදී වන
සංඛ්යාතයට වඩා වැඩි සංඛ්යාතයන්
හෝ අඩු සංඛ්යාතයන් සඳහාද
භාවිතා කළ හැකියි.
මෙවිට
එම වෙනස් සංඛ්යාතයන් සඳහා
ඇන්ටනාව අනුනාදී නොවේ (ඒ
කියන්නේ ප්රතිබාදක අගයක්
දැන් පවතිනවා).
එම ප්රතිබාදක
අගය ඉවත් කිරීමට ඇන්ටනා ඩයිපෝලය
සුදුසු ප්රමාණයකින් කොට
කිරීමට (සංඛ්යාතය
වැඩි වීමේදී)
හෝ සුදුසු
ප්රමාණයකින් දිග කිරීමට
(සංඛ්යාතය
අඩු වීමේදී)
සිදු වේ.
එහෙත් මෙම
ක්රියාවන් දෙකම ප්රායෝගිකව
සිදු නොකරයි (ඇන්ටනා
කියන්නේ නිතරම කොට කළ හැකි
දිගු කළ හැකි දෙයක් නොවෙයිනෙ).
මෙහිදී
කළ හැකි පිලියම වන්නේ ඇන්ටනා
ටියුනර් එකක් පිටතින් සවි
කිරීම වැනි සරල උපක්රමයක්
යෙදීමයි.
මෙය අපට
සිතිය හැකියි ඇත්තටම ඩයිපෝල
දිග වෙනස් නොකර යම් උපක්රමයකින්
සංඥාවට ඩයිපෝල දිග වෙනස් කළා
යැයි පෙන්වීමක් ලෙස (එය
අප සංඥාවට කරන එක්තරා ප්රෝඩාවකි).
මීට පෙර
ඉලෙක්ට්රිකල් ලෙන්ත් යන
සංකල්පය මෙහිදිත් දැන් ආදේශ
කර ගත හැකි තත්වයක් තිබෙනවා
නේද? ඒ
අනුව ඩයිපෝලයේ ෆිසිකල් ලෙන්ත්
එක වෙනස් නොකර,
අර කියූ
ලෙස භාහිර උපක්රමයකින් එහි
ඉලෙක්ට්රිකල් ලෙන්ත් එක
වෙනස් කළ හැකියි.
ඒ කියන්නේ
අපට හැකියි ඩයිපෝලයක් electrically
short කරන්න
හෝ electrically
long කරන්න.
ඉහත
ආකාරයට ඇන්ටනාවේ electrical
length එක ඉතා
කුඩාය.
ඉලෙක්ට්රිකලි
ෂෝට් ඇන්ටනාව ඔම්නිඩිරෙක්ෂනල්
ඇන්ටනාවකි (ඇත්තටම
සෑම සරල ඩයිපෝල් ඇන්ටනාවක්ම
ඔම්නිඩිරෙක්ෂනල් වේ).
එනම්
ඩයිපෝලය වටේටම ඒකාකාරව රේඩියෝ
තරංග පිට වේ.
තරංග
ආයාමයෙන් 1/10
ක් යන
කොන්දේසිය නොකැඩෙන සේ ඩයිපෝල්
දිග වැඩි කරගෙන යන විට ඇන්ටනාවෙන්
වැඩි වැඩියෙන් විකිරණය එලෙස
පිට වේ (එනම්
කාර්යක්ෂමතාව වැඩි වේ).
එහි ඩයිපෝල්
අන්ත දෙකින් විකිරණය වීම ඉතාම
අල්පයි.
ඒ කියන්නේ
සුපුරුදු උළුඳු වඩේ හැඩයට
රේඩියේෂන් පැටර්න් එක ඇත.
මෙවැනි
ඇන්ටනා නැරෝබෑන්ඩ් ඇන්ටෙනා
ලෙස භාවිතා වේ.
ගේන් එක
අයිසොට්රොපික් ඇන්ටනාවට
සාපේක්ෂව 1.77dB
කි.
ඇත්තටම
එය නරක/අඩු
අගයක්ම නොවේ හාෆ්වේව් ඩයිපෝල්
ඇන්ටනාවට සාපේක්ෂව ගත් විට
(හාෆ්වේව්
ඩයිපෝල් ඇන්ටනාවක ගේන් එක
2.14dBi වේ).
ඇන්ටනාවේ
ඉන්පුට් ඉම්පීඩන්ස් අගය
ලැබෙන්නේ පහත සරල සූත්රයට
අනුකූලවයි.
Z
= (Radiation resistance, Rrad
+ Loss resistance, Rloss)
+ j(Reactance, X)
ඉහත
සූත්රයේ සංරචක 3
වෙන වෙනම
ගණනය කරන සූත්ර පහත දැක්වේ.
මෙහි L
යනු ඩයිපෝල්
දිගයි.
ලොස්
රෙසිස්ටන්ස් අගය ගණනය කරන
සූත්රය තුලට චර්මීය ආචරණයේ
බලපෑමද ඇතුලත් කර තිබේ (එනම්
චර්මීය ආචරණ සූත්රය ඒ තුල
ඇත). a යනු
ඩයිපෝල් බටයේ/කූරේ
අරය වේ.
μ යනු
ඇන්ටනා බටයේ පාරගමග්යතාව
වන අතර,
σ යනු එම
බටයේ සන්නායකතාව වේ.
ඉහත
සූත්ර අනුව ඕනෑම රේඩියෝ
සංඛ්යාතයක් සඳහා ෂෝට් ඩයිපෝලයක
ඉහත අගය 3 ගණනය
කර ඇන්ටනාවේ ඉම්පීඩන්ස් අගය
සෙවිය හැකිය. එසේ
සොයා බැලුවොත් පෙනේවි ලොස්
රෙසිස්ටන්ස් අගය හා රේඩියේෂන්
රෙසිස්ටන්ස් අගයන් දෙකෙහිම
එකතුව ඉතා කුඩා අගයක් බවත්,
එම අගයන්
දෙකටම වඩා ඉතා විශාල අගයක්
ප්රතිබාදකය (X) සඳහා
ලැබෙන බවත්. මෙනිසා
මෙවන් ඇන්ටනාවක් ට්රාන්සීවරයකට/ෆීඩ්ලයින්
එකකට සම්බන්ද කිරීමේ ගැටලු
මතු වේ. තවද,
ඩයිපෝලය
කුඩා වන්නට වන්නට රේඩියේෂන්
රෙසිස්ටන්ස් එක විශාල ලෙස
(වර්ග
පදයකින්) අඩු
වී, ඊට
සාපේක්ෂව ලොස් රෙසිස්ටන්ස්
එක වැඩි වේ (ඇන්ටනා
දිග අඩු වන විට ඊට සමානුපාතිකව
ලොස් රෙසිස්ටන්ස් එකද අඩු
වේ); ප්රතිබාධකය
වැඩි වේ. එවිට
ඇන්ටනාව අකාර්යක්ෂම වේ (එනිසා
ඇන්ටනා ඩයිපෝලය කුඩා වන්නට
වන්නට ඇන්ටනා කාර්යක්ෂමතාව
අඩු වේ).
මීට
පෙර අප half-wavelength antenna
ගැන විස්තර
තරමක් සොයා බලා තිබෙන නිසා
වැඩි විස්තර කියන්නට යන්නේ
නැත. දළ
වශයෙන් හාෆ්වේව්ලෙන්ත්
ඩයිපෝලයක ඉම්පීඩන්ස් අගය ඕම්
73 + j42.5 පමණ
වේ. මින්
පේනවා ප්රතිරෝධ අගයට අමතරව
තරමක ප්රතිබාදක අගයකුත්
(ප්රේරක
ප්රතිබාදකයක්) එහි
තිබෙන බව. සාමාන්යයෙන්
මෙම ප්රතිබාදක අගය ඉවත් කළ
හැකියි හරියටම තරංග ආයාමයෙන්
½ ක්
වෙනුවට තරංග ආයාමයෙන් 0.47
ත් 0.48ත්
අතර දිගක් ඩයිපෝල් දිග ලෙස
ගත් විට. මෙහි
ගේන් එක 2.15dBi පමණ
වේ. සුපුරුදු
උළුඳු වඩේක හැඩයට රේඩියේෂන්
පැටර්න් එක ඇති ඔම්නිඩිරෙක්ෂනල්
ඇන්ටනාවකි මෙය. මෙම
ඇන්ටනාව අනෙක් ඇන්ටනා සසඳන
දර්ශීය ඇන්ටනාවකි (reference
antenna).
සටහන
තරංග ආයාමයෙන්
හරි භාගයක් වන සේ සැකසූ හාෆ්වේව්
ඩයිපෝලයක් රෙසෝනන්ට් නොවී
ඊටත් වඩා තව පොඩ්ඩක් කොට කළ
විට රෙසෝනන්ට් වන්නට හේතුව
කුමක්ද? සෛද්ධාන්තිකව
එසේ විය නොහැකියිනෙ.
එහෙත්
ප්රායෝගිකව එසේ වේ. ඊට
හේතුව velocity factor වේ.
ඩයිපෝල්
කූර/බටය
දිගේ විදුලි සංඥාව ගමන් කරන
වේගය ආලෝකයේ වේගයට වඩා අඩුය.
තවද,
ඇන්ටනා
බටයේ/කූරේ
විශ්කම්භය අනුව මෙම වේගය තීරණය
වේ. ඒ
අනුව ඩයිපෝල් කූරේ විශ්කම්භය
තරංග ආයාමයෙන් 0.00001 ක්
තරම් ඉතා සිහින් නම් VF
අගය 0.98
පමණ වන අතර,
කූරේ විශ්කම්භය
තරංග ආයාමයෙන් 0.008 ක්
පමණ මහත නම් එම අගය 0.94 පමණ
වේ. එනිසා
සම්මතයක් ලෙස (එනම්
කූරේ විශ්කම්භය ගැන එතරම්
නොතකා) එම
අගය 0.95ක්
ලෙස සලකමු. ඒ
කියන්නේ සාමාන්ය තරංග ආයාමයට
වඩා 5%ක්
අඩුවෙනුයි ඩයිපෝල් දිග ගත
යුත්තේ. ඇත්තටම
ඕනෑම වර්ගයක ඇන්ටනාවකදී
මෙලෙසයි දිග ගත යුත්තේ (උදාහරණයක්
ලෙස, තරංග
ආයාමයෙන් ½ ක්
ගන්නැයි කියා සිටියත්,
ප්රායෝගිකව
ඉන් 5%ක්
පමණ අඩු දිගකුයි ගත යුත්තේ).
කූරේ විශ්කම්භය
වැඩි කරගෙන යන විට ඇන්ටනාව
එන්න එන්නම වැඩි සංඛ්යාත
පරාසයක් සපෝට් කරන බව ඔබ දන්නවා
(එනම්
ඇන්ටනාව බ්රෝඩ්බෑන්ඩ් වෙනවා).
එය රීතියක්
ලෙස කටපාඩම් කළත්, ඊට
හේතුව ගැන ඔබ සිතා බලා තිබෙනවාද?
ඇන්ටනාවක්
වැඩි සංඛ්යාත පරාසයකට ඔරොත්තු
දෙනවා යැයි කියන්නේ පුලුල්
සංඛ්යාත පරාසයක ඇති සංඥා
සඳහා සාමාන්යයෙන් ඇන්ටනාවේ
සම්බාදක අගය වෙනස් වීම කුඩාය
කියන එකයි. එවිට
ඇන්ටනාව හා ෆීඩ්ලයින් එක අතර
මිස්මැච් එක එම පරාසයේ විවිධ
සංඛ්යාත සඳහා වෙනස් වුවත්,
එම වෙනස
කුඩාය.
කූරේ විශ්කම්භය
වැඩි කරන විට, ඇන්ටනා
ඉම්පීඩන්ස් එක වෙනස් වීම අඩු
වේ. ඒ
කියන්නේ එම ලක්ෂණය ඉහත ඡේදයේ
විස්තර කළ පරිදි පුලුල්
සංඛ්යාතයක් සපෝට් කළ හැකි
තත්වයක් ඇති කරනවා (ඒ
කියන්නේ ඇන්ටනාව බ්රෝඩ්බෑන්ඩ්
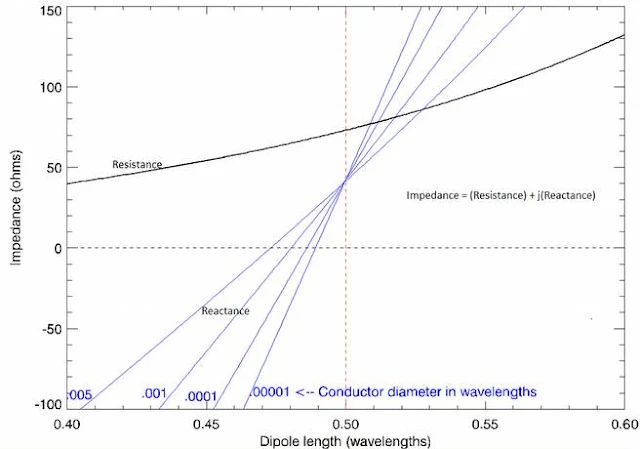
වෙනවා). පහත
ප්රස්ථාරයෙන් මේ බැව් පැහැදිලි
වෙනවා. බලන්න
කූරේ විශ්කම්භය මහත් වන්නට
වන්නට ප්රස්ථාර රේඛාවේ
(නිල්පාට
රේඛා) ඇලය
අඩු වෙනවා (ප්රස්ථාර
රේඛාවක ඇලය අඩු වෙනවා යනු
ප්රස්ථාරයේ සිරස් අක්ෂයෙන්
පෙන්වන ගතිගුණය මොට කරන බවයි;
එම ගතිගුණය
විචලනය වීම අඩු කරන බවයි).
දැන්
අපි බලමු වෙනත් දිගකින් යුත්
ඩයිපෝල් ඇන්ටනා ගැන. පහත
දැක්වෙන්නේ තරංග ආයාමයට
සාපේක්ෂව වෙනස් අනුපාත අගයන්
4ක්
සඳහා වූ ඩයිපෝල 4ක්
හා එහි ඩයිපෝල් මත ධාරාව හා
වෝල්ටියතාව පිහිටන ආකාරය
පෙන්වන ආකෘති වේ. ඒ
සෑම ඩයිපෝලයකටම සංඥා විදුලිය
සපයන්නේ ඩයිපෝලය මැදිනි.
හැමවිටම
ඩයිපෝලය කෙලවරවල්වල ධාරාව
ශූන්ය විය යුතු අතර වෝල්ටියතාව
උපරිම විය යුතුයි. එසේ
සයිනාකාර අර්ධතරංග කෙලවරවල්
දෙපැත්තේ සිට මැද දක්වා අඳින්න.
එච්චරයි.
ඉතිං ඕනෑම
තරංග ආයාම අනුපාතයක් සඳහා
ධාරා හා වෝල්ටියතා වක්ර එම
රීතිය අනුව ඉතා පහසුවෙන්ම
සිතා ගත හැකියි. මෙවැනි
රූපවලින් අපට පහසුවෙන්ම
ඇන්ටනාවේ ඉම්පීඩන්ස් අගය ගැන
අදහසක් ගත හැකිය.
ඉලෙක්ට්රිකලි
ෂෝට් ඇන්ටනාවේ ෆිඩ්ලයින්
එකෙන් ඊට සංඥා ඇතුලු කරන
ස්ථානයේදී ධාරාව (කලු
පාට වක්රය) උපරිම
වන අතර වෝල්ටියතාව (කොලපාට
වක්රය) අවම
වේ. එනිසා
සම්බාධක අගය (වෝල්ටියතාව
ධාරාවෙන් බෙදූ විට) ඉතා
අවම වේ (සම්බාදකයේ
තිබෙන ප්රතිබාදක අගය මොහොතකට
අමතක කර ප්රතිරෝදී අගය පමණක්
මෙහි සලකා බලමු). තවද
මෙම ෂෝට් ඇන්ටනාවේ ධාරා හා
වෝල්ටියතාවල විශේෂත්වයක්ද
ඇත. එනම්,
ඒවායේ හැඩය
වක්රාකාර නොව රේඛීය වේ.
ඊට හේතුව
ඕනෑම වක්රයක ඉතා කුඩා කොටසක්
පමණක් ගත් විට එම කොටසේ වක්ර
ස්වභාවය අවම වී රේඛීයව පෙනේ
(ඒකනෙ
පොලොව වක්රාකාර වුවත්,
කෙටි දුරවල්
සඳහා එම වක්රතාව දැනෙන්නේ
නැත්තේ). එනිසා
ඉලෙක්ට්රිකලි ෂෝට් ඩයිපෝලයකදී
තරංග ආයාමයට සාපේක්ෂව ඩයිපෝල්
දිග ඉතා කුඩා නිසා එම කුඩා දිග
මත ධාරාවේ හා වෝල්ටියතාවේ
වක්රාකාර හැඩයෙන් යුතු විචලනය
පෙන්වීමට අවස්ථාවක් නැත.
එලෙසම
දෙවැනි ඇන්ටනාවේ (තරංග
ආයාමයෙන් කාලක් දිග ඇන්ටනාව
– quarter-wavelength antenna) ගැන
බැලුවොත් එහිදිත් සම්බාදක
අගය අවම බව පේනවා.
එහෙත්
තරංග ආයාම 1ක්
දිග ඇන්ටනාව (full-wavelength
antenna හෙවත්
full-wave antenna) බලන්න.
එම ඩයිපෝලය
මැද වෝල්ටියතාව උපරිම වන අතර,
ධාරාව අවම
වේ. එනිසා
එහි සම්බාදක අගය ඉතා විශාලය.
තරංග
ආයාම 1.5ක්
දිග ඩයිපෝලය සලකන විට,
එහි මැද
ධාරාව උපරිම හා වෝල්ටියතාව
අවම නිසා සම්බාදක අගයද අවම
වේ. මෙම
ලක්ෂනය පහත ප්රස්ථාරයෙන්
පෙන්විය හැකිය. පහත
ප්රස්ථාරයේම තරංග ආයාමය 0.6
දක්වා වූ
කොටසකි ඉහත සටහන තුල ඇති
ප්රස්ථාරයත්. ඉහත
ප්රස්ථාරයේ අමතරව ඩයිපෝල්
විශ්කම්භ කිහිපයක් දක්වා
තිබේ.
ඉහත
ඡේදයේ විස්තර කළ ලක්ෂන ඉහත
ප්රස්ථාරයේ පෙනේ. ඊට
අමතරව ඉහත විස්තරය තුල අමතක
කර දැමූ සම්බාදක අගය තුල තිබෙන
ප්රතිබාධක අගය (+ සහිත
වක්රයෙන්) විචලනය
වන අයුරුද මෙම ප්රස්ථාරයේ
දැක්වේ.
ඉහත
ඩයිපෝල දිග තරංග ආයාමයට සාපේක්ෂව
ඉතා කුඩා අගයක සිට 1.5ක
ගුණාකාර/අනුපාත
අගයක් දක්වා සම්බාදක අගය
විචලනය වන අයුරු ප්රස්ථාර
ගත කර තිබුණත්, ඩයිපෝලයේ
දිග 1.5 ගුණාකාර
අගයටත් වඩා වැඩිවිය හැකියි
(අවශ්ය
නම්). මෙවිට
සම්බාදක අගය විචලනය වන අයුරු
තර්කානුකූලව ඔබට තේරුම් ගත
හැකියි. ඉහත
රූපයට පෙර රූපයේදී ඩයිපෝලය
මත ධාරාව හා වෝල්ටියතාව පිහිටන
ආකෘතිය සාදා ගත් විට,
ඩයිපෝලයේ
සම්බාදක අගය ගැන ඉබේම වැටහේ.
උදාහරණයක්
ලෙස, දැන්
බලමු තරංග ආයාම 2.2ක
පමණ දිගක් ඇති ඩයිපෝලයක කොහොමද
ධාරාව හා වෝල්ටියතාව පිහිටන්නේ
කියා පෙර සඳහන් කළ රීතියට
අනුව.
බලන්න,
ඩයිපෝලයේ
දෙකෙලවරදී ධාරාව ශූන්ය වන
අතර වෝල්ටියතාව (කොලපාට
වක්රය) උපරිම
වේ. එයනෙ
රීතිය. එවිට
සයිනාකාර අර්ධතරංග/අර්ධගෝල
බැඟින් ඩයිපෝල් කෙලවර සිට
ක්රමයෙන් ඩයිපෝලයේ මැද දක්වා
ඇඳ ඇත. එවිට
ඩයිපෝලයේ මැද කොටසේ සෑදෙන
ධාරා හා වෝල්ටියතා වක්ර හැඩය
තමයි තීරණාත්මක වන්නේ එම
ඇන්ටනාවේ සම්බාදක අගය ගැන
අදහසක් ගැනීමට. ඉහත
රූපය අනුව පැහැදිලි වෙනවා,
මැද වෝල්ටියතා
අගය මෙන්ම ධාරා අගයද යම් ඉහල
මට්ටමක තිබෙන බව. එවිට
මෙම උදාහරණයේදීත් සම්බාදක
අගය අඩු අගයකි (මොකද
ඉහල අගයක් තවත් ඉහල අගයකින්
බෙදූ විට පිලිතුර කුඩා අගයක්නෙ
ලැබෙන්නේ).
දැන්
ඉහත ඩයිපෝලය මත ධාරාව පිහිටන
ආකාරය මත රේඩියේෂන් පැටර්න්
එකත් දළ වශයෙන් සිතා ගත හැකිය.
රේඩියේෂන්
පැටර්න් එකෙන් කියන්නේ ඇන්ටනාව
අවට පරිසරයට රේඩියෝ විකිරණය
පිට වන ආකාරයනෙ. සංඥා
ධාරාවක් ඩයිපෝලය මත යම් තැනක
තිබේ නම්, එතැනින්
විකිරණය පිට වේ. එවිට
ධාරාව වැඩියි නම් විකිරණයද
වැඩිය. අන්න
ඒ ආකාරයෙන් සිතූ විට රේඩියේෂන්
පැටර්න් එකත් දළ වශයෙන් සිතින්
මවා ගත හැකිය.
ඇත්තටම,
ඩයිපෝල අගය
තරංග ආයාම 1ක
දිගක් දක්වා සියලුම ඇන්ටනාවල
රේඩියේෂන් පැටර්න් එක සුපුරුදු
උළුදු වඩේ හැඩය වේ. මෙහිදී
වුවද, ඩයිපෝල
දිග අනුව හැඩයේ කුඩා වෙනස්කම්
ඇති වේ (සමස්ථ
හැඩය වෙනස් නොවූවත්).
තරංග
ආයාම 1කට
වඩා ඩයිපෝලය දික් වන විට,
ඉහත පොදු
හැඩය නැති වේ. මෙවිට
උළුඳු වඩය වැනි හැඩ කිහිපයක්
ඩයිපෝලය දිගේ ඇති වේ.
උදාහරණයක්
ලෙස පහත දැක්වෙන්නේ තරංග ආයාම
1.5ක
දිගක් සහිත ඩයිපෝලයක රේඩියේෂන්
පැටර්න් එක වේ.
සටහන
phase
length
සංඥා ගමන්
කරන සන්නායකයක දිග සාමාන්ය
පරිදි මීටර්, අඩි
වැනි ඒකකනෙ යොදා ගන්නේ.
එහෙත් ඉහත
ඡේද දෙක තුන ගැන විතරක් නැවත
බලමු. එහිදී
මා ඇන්ටනා දිග අඩි හෝ මීටර්වලින්
නොවේ ප්රකාශ කළේ; “තරංග
ආයාම අච්චරක් මෙච්චරක්” වැනි
ආකාරයෙනි. මෙම
ආකාරයට කියනු ලබන දිග phase
length ලෙස
හැඳින් වේ. මේ
ක්රම දෙකෙහි විශාල වෙනසක්
ඇත. එනම්
පළමු ක්රමය සන්නායකය හරහා
යන සංඥා සංඛ්යාතය මත රඳා
පවතින (frequency-dependent) අතර,
දෙවැන්න
සංඛ්යාතය මත රඳා නොපවතී
(frequency-independent). එනිසා
දෙවැනි ක්රමයෙන් පොදුවේ
ඕනෑම සංඥා සංඛ්යාතයක් සඳහා
වලංගු වේ.
මෙම වෙනස
උදාහරණයකින්ම බලමු.
සිතන්න යම්
ඩයිපෝලයක දිග මීටර් 1.5ක්
කියා. මෙවිට
එම සරල ඩයිපෝලය අනුනාදි වන්නේ
මෙගාහර්ට්ස් 100ක
සංඥාවකටයි (300,000,000/100,000,000 =
3 → 3/2 = මීටර්
1.5). මෙගාහර්ට්ස්
200 ක හෝ
වෙනත් ඕනෑම සංඛ්යාතයකට මෙම
ඩයිපෝල් දිග ගැලපෙන්නේ නැත.
එවිට ඒ ඒ
සංඛ්යාතය සඳහා වෙන වෙනම
ඩයිපෝල් දිග මීටර්වලින් (හෝ
වෙනත් ඒකකයකින්) ඉදිරිපත්
කළ යුතු වෙනවා. එහෙත්
ඩයිපෝල් දිග තරංග ආයාම යන පොදු
ඒකකයෙන් ලබා දුන් විට ඇති වන
තත්වය බලමු. අර
ඇන්ටනාවම ගමු. දැන්
ඩයිපෝලයේ දිග තරංග ආයාම භාගයකි.
මෙවිට ඕනෑම
සංඛ්යාතයක් සඳහා මෙම ප්රකාශය
වලංගුය (එක්
එක් සංඛ්යාතයට වෙනස් වෙනස්
අගයන් ඉදිරිපත් කිරීමට අවශ්ය
නැත).
තරංග ආයාම
වෙනුවට phase
length ඉදිරිපත්
කළ හැකියි කෝණ අගයක් ලෙසත්.
කෝණ අගය අංශක
(degree) යන
සම්මත නොවන (නමුත්
කවුරුත් දන්නා ජනප්රිය)
ඒකකයෙන් හෝ
සම්මත (නමුත්
එතරම් ජනප්රිය නොවන)
රේඩියන්
(radian) ඒකකයෙන්
දැන් ප්රකාශ කළ හැකියි (අංශක
හා රේඩියන් ගැන මීට පෙර අප කතා
කර තිබෙනවා). එක්
තරංග ආයාමයක් යනු කෝණ අගයක්
ලෙස ගත් විට අංශක 360කි;
රේඩියන් 2π
වේ.
එවිට තරංග
ආයාම ½ ක්
යනු අංශක 180කි;
රේඩියන්
π
වේ.
තරංග ආයාම
¼ ක්
යනු අංශක 90කි;
රේඩියන්
π/2
වේ.
තරංග ආයාම
2ක්
යනු අංශක 720කි;
රේඩියන්
4π
වේ.
මේ ආදි
ලෙස ඕනම තරංග ආයාමයක් කෝණ
අගයකට පහසුවෙන්ම පත් කර ගත
හැකියි.
උදාහරණයක්
ලෙස, අංශක
270ක
ඩයිපෝලයක් යනු තරංග ආයාම ¾
ක් දිගකි.
ඕනෑම සරල ඩයිපෝල් ඇන්ටනාවක කූරු තිරස්ව තිබෙන පරිදි හෝ සිරස්ව තිබෙන පරිදි රැඳවිය හැකියි. මීට පෙර අප ඇන්ටනා පොලරයිසේෂන් ගැන විස්තරාත්මකව කතා කර තිබෙන නිසා තිරස් හා සිරස් රැඳවීමෙහි ඇති වෙනස ඔබට වටහ ගත හැකිය.
සරල
ඩයිපෝල් ඇන්ටනා සෑදීම ඉතාම
පහසු බව ඔබට දැන් වැටහෙනු ඇත.
දැන් අපි
බලමු ඉහත සරල ඩයිපෝල් ඇන්ටනාව
පාදක කොට ගෙන අවබෝධ කර ගත හැකි
ඇන්ටනා වර්ග කිහිපයක් ගැනත්.



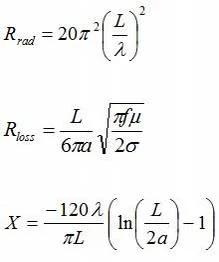





සුපර්..ජයවේවා..දිගටම කරගෙන යන්න..බොහෝම ස්තුතී ඔබට
ReplyDelete:)
Delete