සන්නිවේදනය හා ආධුනික ගුවන් විදුලිය (Amateur radio) 106

Off-Center Fed Dipole Antenna

සරල ඩයිපෝල් ඇන්ටනා බටයේ දිග කුමක් වුවත්, ඊට සංඥා විදුලිය සැපයුවේ මැදින්ය. එනිසා එවැනි ඩයිපෝල් Center-Fed Dipole කියාද හැඳින්වෙනවා. එහෙත් ඩයිපෝලයේ මැදින් නැතිව වෙනත් තැනකින් වුවද සංඥාව ඊට ඇතුලු කළ හැකි අතර මෙවන් ඩයිපෝල් සියල්ලම Off-center Fed (OCF) Dipole ලෙස හැඳින්වෙනවා. ඇන්ටනා ඩයිපෝලයකට ෆීඩ්ලයින් එකක් හරහා සංඥා සපයන ස්ථානය feed point ලෙස හැඳින්වෙනවා. මෙවන් ඇන්ටනාවක් තරංග ආයාම කිහිපයක් සපෝට් කරනවා; එනම් ඇන්ටනාව මල්ටිබෑන්ඩ් වේ.

සාමාන්‍යයෙන් මෙම ඩයිපෝලයක සම්පූර්ණ දිග තරංග ආයාමයෙන් භාගයකි. සෙන්ටර්-ෆෙඩ් හාෆ්වේව්ලෙන්ත් ඩයිපෝලයක නම් සම්භාදකය ඕම් 75 අසල අගයක් වුවත් මෙවන් ඩයිපෝලයක සම්බාදක අගය ඊට වඩා වැඩි වේ. එම අගය දළ වශයෙන් සෙවීමට සූත්‍රයක් ඇත. ඇත්තටම පහත සූත්‍රයෙන් සොයන්නේ OCF ඩයිපෝලයක රේඩියේෂන් රෙසිස්ටන්ස් එකයි (මීට පෙර අප ඉගෙන ගත්තා ඇන්ටනාවේ සම්බාදක අගය හා රේඩියේෂන් රෙසිස්ටන්ස් එක අතර පවතින සම්බන්දතාව). මෙහි x යනු ඩයිපෝල් කෙලවර සිට ෆීඩ් පොයින්ට් එකට ඇති දුර වේ.

ඉහත රූපයේ ocf ඩයිපෝලය සඳහා රේඩියේෂන් රෙසිස්ටන්ස් එක ගණනය කරමු මීටර් 50ක තරංග ආයාමයක් සඳහා. එවිට සමස්ථ ඩයිපෝල් දිග මීටර් 25කි. එම අගයෙන් 1/3 ක් යනු මීටර් 8.3කි (එනම් x = 8.3). දැන් මෙම අගය ඉහත සූත්‍රයට ආදේශ කළ විට, ඕම් 100ක් ලැබේ. මෙම x දුර අඩු වන විට රේඩියේෂන් රෙසිස්ටන්ස් එක වැඩි වේ. සෛද්ධාන්තිකව ඩයිපෝල් කෙළවරේදී (x=0) රේඩියේෂන් රෙසිස්ටන්ස් අගය අනන්තයකි (ප්‍රායෝගිකව ඕම් දෙතුන් දහක් පමණ වේවි). ෆීඩ්ලයින් එකේ සම්බාදක අගය හා ඇන්ටනාවේ සම්බාදක අගය ගැලපෙන්නේ නැති නිසා current balun නම් උපාංගයක් සවි කළ යුතු වෙනවා (බැලන් ගැන පසුව බලමු). ඇන්ටනාව රඳවන උස අනුවත් මෙම බැලන් එකේ අනුපාතය වෙනස් වෙනවා.

සටහන

ඇන්ටනා පොදුවේ symmetrical (හෝ balanced) හා asymmetrical (හෝ unbalanced) ලෙස වර්ගීකරණය කළ හැකිය. බැලැන්ස්ඩ් ඇන්ටනාවකදී ඊට සපයන සංඥා ධාරාව ඩයිපෝල් කූරු (හෝ ඩයිපෝලයට සමාන කොටස්) දෙකේ සමානව ගමන් කරයි. ඒ අනුව සෙන්ටර්-ෆෙඩ් ඩයිපෝල් ඇන්ටනා බැලැන්ස්ඩ් වේ. අන්බැලැන්ස්ඩ් ඇන්ටනාවකදී සංඥා ධාරාව අසමානව ඩයිපෝල් කූරු දෙකේ ගමන් කරයි. දැන් මේ කතා කරමින් සිටින ඕෆ්-සෙන්ටර් ඩයිපෝලය හා ක්වාර්ටර්වේව්ලෙන්ත් මොනෝපෝල් ඇන්ටනාව අන්බැලැන්ස්ඩ් වේ.

ඇන්ටනාව මෙන්ම ෆීඩ්ලයින් එකද balanced හා unbalanced ලෙස වර්ගීකරණය කෙරේ. එහිදී ෆීඩ්ලයින් එකේ සිග්නල් පාත් එක වශයෙන් ක්‍රියා කරන සන්නායකය හා රිටර්න් පාත් එක වශයෙන් ක්‍රියා කරන සන්නායකය යන දෙකේ ගමන් කරන සංඥා විදුලිය පොලොවට (ග්‍රවුන්ඩ් විභවයට) සාපේක්ෂව අසමාන නම් එය අන්බැලැන්ස්ඩ් වන අතර, සමාන නම් බැලැන්ස්ඩ් වේ. මේ ගැන මීට පෙරත් කතා කර තිබෙනවානෙ.

උදාහරණයක් ලෙස සාමාන්‍ය කොඇක්සියල් කේබලය අන්බැලැන්ස්ඩ් වේ. ඊට හේතුව මෙයයි. කේබලයේ මැද කම්බිය පොලොවට සම්බන්ද කර නැත (අර්ත් කර නැත). එනිසා එහි පොලොවට සාපේක්ෂව යම් විභවයක් තිබේ (පොලොවේ විභවය හැමවිටම ශූන්‍යයිනෙ). එහෙත් එහි රිටර්න් පාත් එක වන ෂීල්ඩ් එක සාමාන්‍යයෙන් පොලොවට අර්ත් කර ඇත. ඒ කියන්නේ එම කම්බිය හරහා ධාරාවක් පැමිණියත් පොලොවට අර්ත් කර ඇති නිසා පොලොවට සාපේක්ෂව එහි විභවය ශූන්‍ය වේ. ඒ කියන්නේ මැද කම්බිය හා ෂීල්ඩ් එකේ එකිනෙකට වෙනස් විභවයන් තිබේ; අන්බැලැන්ස්ඩ් වේ.

එහෙත් පැරලල් කේබල් බැලැන්ස්ඩ් වේ මොකද එහි කම්බි දෙකින් එකක්වත් අර්ත් කර නැති අතර, පොලොවට සාපේක්ෂව එම කම්බි දෙකේ විභවය සමාන වේ. තවද, අවශ්‍ය නම් කොඇක්සියල් කේබල් දෙකක් එකට ගෙන බැලැන්ස්ඩ් කේබලයක් සාදා ගත හැකිය. එහිදී කොඇක්ස් කේබල් දෙකේ මැද කම්බි දෙක සිග්නල් පාත් හා රිටර්න් පාත් ලෙස භාවිතා කළ හැකියි (එම කම්බි දෙකින් එකක්වත් අර්ත් නොකර). එම කේබල් දෙකෙහි ෂීල්ඩ් දෙක එකිනෙකට කනෙක්ට් කර අර්ත් කළ හැකියි. මෙමඟින් කොඇක්සියල් කේබල්වල තිබෙන වාසිද ලැබෙන අතර, සංයුක්ත කේබලය බැලැන්ස්ඩ් ද වේ.

සාමාන්‍යයෙන් බැලැන්ස්ඩ් ඇන්ටනාවකට සම්බන්ද කළ යුත්තේ බැලැන්ස්ඩ් ෆීඩ්ලයින් එකක් හා අන්බැලැන්ස්ඩ් ඇන්ටනාවකට සම්බන්ද කළ යුත්තේ අන්බැලැන්ස්ඩ් ෆීඩ්ලයින් එකකි (සම්බාදක අගයන්ද හැකි පමණ සමාන විය යුතුය). එහෙත් ප්‍රායෝගිකව එසේ නොකරන අවස්ථා බහුලවම හමු වේ. මෙවිට බැලන් නම් උපාංග භාවිතා කිරීමට සිදු වේ.

Harmonic Antenna

සාමාන්‍ය සෙන්ටර්-ෆෙඩ් ඇන්ටනාවක් වුවද ඇත්තෙන්ම මල්ටිබෑන්ඩ් වේ; එය ඉබේම සිදු වන දෙයකි. එනම්, යම් රෙසෝනන්ට් ඇන්ටනාවක් සංඥා තරංග ආයාමයෙන් ½ කටනෙ (half-wavelength) සකස් කරන්නේ. මෙම ඇන්ටනාවම එම හාෆ්වේව්ලෙන්ත් හි 3, 5 ආදී ඔත්තේ ගුණාකාරවලටද (උපරිතාන - harmonic) රෙසෝනන්ට් වේ. යම් ඇන්ටනාවක් එහි යම් උපරිතාන සංඛ්‍යාතයක් සඳහා යොදා ගන්නා විට, ඊට harmonic antenna යැයි කිව හැකිය.

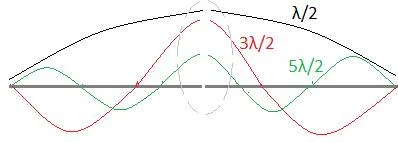
උදාහරණයක් ලෙස සෙන්ටර්-ෆෙඩ් හාෆ්වේව්ලෙන්ත් ඩයිපෝල් ඇන්ටනාවක් සලකමු. එහි මූලික සංඛ්‍යාතය (තරංග ආයාමය) හා එහිම තෙවැනි හා පස්වැනි ඔත්තේ උපරිතාන සංඥා ඇන්ටනා ඩයිපෝලය මත පිහිටන ආකාරය ඉහත දැක්වේ. එහි මැද (ෆීඩ් පොයින්ට් එකේ) ධාරා වක්‍ර පිහිටන අයුරු බලන්න (වෝල්ටියතා වක්‍රද අනුරූපව පිහිටනවා). අලුපාට කඩඉරි රවුම තුල බලන්න. සෑම තරංගයකම උපරිම ධාරාව පවතින්නේ ෆීඩ්පොයින්ට් එකේ නේද? ඒ කියන්නේ සම්බාදක අගය එතරම් වෙනස් නොවේ ඔත්තේ උපරිතානවලදී.

සංඛ්‍යාත්මකව උදාහරණයක් බලමු. සිතමු ඉහත රූපයේ ඇත්තේ මීටර් 40ක් දිග තරංග ආයාමයක් සඳහා සාදපු හාෆ්වේව්ලෙන්ත් ඇන්ටනාවක් කියා. එවිට එම ඩයිපෝලයේ දිග මීටර් 20කි. මීටර් 40 ක තරංග ආයාමය සහිත තරංගයේ සංඛ්‍යාතය 300,000,000/40 = 7.5MHz වේ. මෙම ඩයිපෝලයම තෙවැනි උපරිතානයත් සපෝට් කරනවනෙ. ඒ කියන්නේ 7.5 x 3 = 22.5MHz යන සංඛ්‍යාතය සහිත සංඥා සඳහාත් ඩයිපෝලය භාවිතා කළ හැකියි. මෙවිට ඊට හාර්මනික් ඇන්ටනාවක් ලෙස ක්‍රියා කරනවා යැයි කියනවා. එලෙසම 7.5x5 = 37.5MHz සඳහාත් එය හාර්මනික් ඇන්ටනාවකි.

(ෆීඩ් පොයින්ට් එක ඇන්ටනා කූරේ දුරින් 1/3 ක් කෙලවරට වන්නට ඇති) ඕෆ්-සෙන්ටර් ෆෙඩ් ඇන්ටනාවක්ද හාර්මනික් ඇන්ටනාවක් ලෙස භාවිතා කළ හැකිය. එහෙත් මෙහිදී මූලික සංඛ්‍යාතයේ ඉරට්ටේ උපරිතානයි එය සපෝට් කරන්නේ. උදාහරණයක් ලෙස, 7MHz ඇන්ටනාව 7x2 = 14MHz, 7x4 = 28MHz ආදී සංඛ්‍යාතයන්ටද වලංගු වේ.

ආධුනික ගුවන් සේවා බෑන්ඩ් බලන විට එහි අවසංඛ්‍යාතය පැත්තේ බෑන්ඩ්වල කදිම සම්බන්දතාවක් පවතිනවා. එනම් පහල බෑන්ඩ් harmonically related (උපරිතානමය වශයෙන් සම්බන්ධිතයි; එනම් එක් එක් බෑන්ඩ් අතර නියත අනුපාතයක් ඇත) වේ. බලන්න ආධුනික බෑන්ඩ් තිබෙනවානේ මීටර් 160, 80, 40, 20, 10 ලෙස. මෙහි 2හි ගුණාකාර (උපරිතාන) ලෙස නේද තිබෙන්නේ? ඉතිං ocf ඇන්ටනාවක් ඉරට්ටේ උපරිතාන සපෝට් කරන නිසා මෙම බෑන්ඩ් කිහිපයක් සඳහාම තනි ඇන්ටනාවක් භාවිතා කළ හැකියි. මෙලෙසම තවත් ඇමචර් බෑන්ඩ් තිබෙනවා 2හි ගුණාකාර ලෙස පවතින.

Folded Dipole

ඉහතදී ඩයිපෝලය කූරු දෙකක් වශයෙනුයි පැවතියේ. එහෙත් ඩයිපෝලයේ දිග පහත ආකාරයට සෑදූ විට ඊට folded dipole කියා කියනවා. මෙහිදී ඇන්ටනාව සපෝට් කරන සංඛ්‍යාත පරාසය තරමක් පුලුල් වේ (එනම් බ්‍රෝඩ්බෑන්ඩ් වේ). සාමාන්‍යෙයන් පහත රූපයේ පෙන්වා ඇති ආකාරයට තරංග ආයම භාගයක් වශයෙනුයි එය සාදන්නේ. රේඩියේෂන් පැටර්න් එක සාමාන්‍ය හාෆ්වේව්ලෙන්ත් ඩයිපෝල් ඇන්ටනාවක මෙන්මය. මෙහි h උස තරංග ආයාමයට වඩා ඉතාම කුඩා විය යුතුය.

ඇන්ටනාවේ ඉන්පුට් ඉම්පීඩන්ස් අගය 2²=4 ගුණයකින් වැඩි වේ. ඉම්පීඩන්ස් අගය 2හි වර්ගයකින් වැඩි වන්නට හේතුව සරලව තර්ක කර දැනගත හැකියි මෙලෙස. සරල හාෆ්වේව්ලෙන්ත් ඩයිපෝලයක ධාරාව ගලන/පිහිටන හැටි පෙන්වන පහත රූපය බලන්න. ධාරාව එකම පැත්තකට ගලයි (රූපයේ දකුණු පැත්තට ඇඳ තිබුණත්, මෙම දිශාව ආවර්තිකව මාරු වේ).

දැන් ඉහත දිග මෙන් දෙගුණයක දිගක් ගත් විට ධාරාව පහත ආකාරයට පිහිටනු ඇත. වැඩිපුර සම්බන්ද කළ හාෆ්වේව්ලෙන්ත් එක සමාන කොටස් දෙකක් වශයෙන් ඉහත ඩයිපෝලය දෙපසට සවි කර ඇත (දම්පාටින්). මෙහිදී තිරස් රේඛාවෙන් උඩ තිබෙන සයිනාකාර ධාරා අර්ධය ගමන් කරන දිශාවට විරුද්ධ දිශාවටයි තිරස් අක්ෂයෙන් පහල තිබෙන සයිනාකාර ධාරා අර්ධය ගමන් කරන්නේ. එනිසා දම්පාටින් දක්වා තිබෙන සන්නායක කොටස්වල ධාරාව ගලා යන්නේ කලුපාටින් දක්වා තිබෙන කොටසට විරුද්ධ පැත්තටයි.

ඉහත රූපයම පහත රූපයේ ආකාරයට සාදා ගත හැකිය. මෙහිදී දම්පාට කොටස් දෙක උඩදී තනි කොටසක් බවට පත් වේ. මේ තිබෙන්නේ ෆෝල්ඩඩ් ඩයිපෝලය නේද? සන්නායක දෙකෙහි ධාරාව ගලා යන්නේ එකම පැත්තට බව දැන් පැහැදිලි වෙනවා.

දැන් ඩයිපෝලයේ විදුලි ධාරාව එකම දිශාවට ගලා යෑමට මාර්ග 2ක් තිබෙනවා (ඩයිපෝලයේ යට කූරු හා උඩු කූරු). ඒ කියන්නේ සංඥා ධාරාව 2ට බෙදී යනවා. එසේ වුවත් ඇන්ටනාවට සපයන සංඥා ජවය වෙනස් වන්නේ නැහැනෙ. එම ජව අගය I²R යන සූත්‍රය අනුව, ධාරාව ½ කින් අඩු වන විට එහි වර්ග වීම නිසා (½)² = ¼ ක් බවට පත් වන නිසා එම අඩු වීම නැති කිරීමට එහි ඇති R පදය 4 ගුණයක් විය යුතුයිනෙ (මොකද ජවය නොවෙනස්ව පැවතිය යුතු නිසා). ඒ කියන්නේ සම්බාදකය 4 ගුණයකින් වැඩි වෙනවා. උදාහරණයක් ලෙස, තරංග ආයාමයෙන් ½ ක් ලෙස තිබෙන පරිදි සෑදූ ෆෝල්ඩඩ් ඩයිපෝලයක සම්බාදක අගය දළ වශයෙන් 75x4 = 300 ඕම් පමණ වේ. එනිසා ඕම් 300 පැරලල් ෆීඩ්ලයින් මේ සඳහා යොදා ගත හැකියි.

සෙන්ටර්-ෆෙඩ් ෆෝල්ඩඩ් ඩයිපෝල් ඇන්ටනාවක්ද එහි මූලික තරංග ආයාමයට මෙන්ම ඔත්තේ හාර්මොනික්වලට රෙසෝනන්ට් වේ. ෆීඩ් පොයින්ට් එක හරි මැදින් නැතිව කෙලවරට බරව (1/3ක්) තැබුවොත් ඉරට්ටේ හාර්මොනික්වලට රෙසෝනන්ට් වන පරිදි සාදා ගත හැකිය. මෙවිට සම්බාදක අගයද විශාල ලෙස වෙනස් වන බව පැහැදිලියිනෙ. සුපුරුදු ලෙසම මෙම ඇන්ටනාවත් වර්ටිකල් හෝ හොරිසොන්ටල් ආකාරයට රැඳවිය හැකිය.

ෆෝල්ඩඩ් ඩයිපෝලය හාෆ්වේව්ලෙන්ත් ඩයිපෝල් දිගවල් දෙකක් සමාන්තරගතව තිබෙනවා යැයි සැලකිය හැකිය. අවශ්‍ය නම් පහත රූපයේ ආකාරයට හාෆ්වේව්ලෙන්ත් ඩයිපෝල් දිගවල් 3ක් සමාන්තරගතව ඇති කළ හැකිය. මෙවිට සරල ඩයිපෝලය හරහා මුලින් ගමන් කළ ධාරාව 1/3 කින් අඩු වෙනවා මොකද සන්නායක මාර්ග 3ක් ඔස්සේ එම ධාරාව ගලා යන නිසා. එවිට, (1/3)² = 1/9 කින් ධාරාව අඩු වන නිසා, සම්බාදකය 9 ගුණයකින් වැඩි විය යුතුයි. සන්නායක 3ක් ඇති විට එහි සම්බාදකය අගය ඕම් 600 ට ආසන්නව ලැබේ. එවැනි දිගවල් 4ක්, 5ක් ආදි වශයෙනුත් එකතු කර බැලිය හැකිය. මෙවිට සම්බාදක අගය ඉහත පැහැදිලි කළ විදියට ක්‍රමයෙන් වැඩි වේ.

සන්නායක 2ක් හෝ කිහිපයක් ඉහත ආකාරයට යොදා ගත් විට සම්බාදක අගය වැඩි වන අයුරු දැන් අප දන්නවා. සාමාන්‍යයෙන් මෙම කූරු/සන්නායකවල ගනකම සමාන වේ. එහෙත් එම කූරුවල ගනකම එකිනෙකට වෙනස් වන විට සම්බාදක අගයද වෙනස් වේ. පහත දැක්වෙන්නේ සාමාන්‍ය ෆෝල්ඩඩ් ඩයිපෝලයක (එනම් සන්නායක දෙකක් ඇති අවස්ථාව) එම සන්නායකවල ගනකම (විශ්කම්භය) වෙනස් ආකාරයෙන් පවතින අවස්ථාවයි.

ඉහත d1, d2, h යන පරාමිතින් ඇතුලත් පහත ආකාරයේ සූත්‍රයක් ඇත. මෙම සූත්‍රයෙන් ලැබෙන අගයෙන් කියන්නේ මෙම පරාමිතින් පමණක් වෙනස් කළ විට සාමාන්‍යයෙන් (එනම් සන්නායක ගනකමවල් සමාන විට) ලැබෙන සම්බාදක අගය වෙනස් වන ගුණාකාරයයි. එනම්, එම සූත්‍රයෙන් ලැබෙන r අගයෙන් වැඩි කළ යුතු වෙනවා ෆෝල්ඩඩ් ඩයිපෝලයේ සාමාන්‍ය සම්බාදක අගය. තවද, සන්නායකවල ගනකම් සමාන වන විට, r=1 බවට පත්ව සූත්‍රයේ බලපෑම නැති වෙන බවත් පේනවා නේද?

folded dipole එකක විශේෂිත වාසි ඇත. සමහර අවස්ථාවලදී සරල ඩයිපෝලයේ සම්බාදක අගය විවිධ ප්‍රායෝගික හේතු නිසා ඉතා කුඩා වේ (යැගී ඇන්ටනාවලදී මේ ගැන සලකා බලමු). ෆෝල්ඩඩ් ඩයිපෝලයක් යොදා ගෙන එසේ අඩු වන සම්බාදක අගය කිහිප ගුණයකින් (4 හෝ 9 හෝ) අවශ්‍ය පරිදි වැඩි කර ගත හැකිය.

සටහන

Coaxial Cable

විවිධ ගතිගුණ ඇති කොඇක්සියල් කේබල් වර්ග කිහිපයක් ඇත. කැරක්ටරිස්ටික් ඉම්පීඩන්ස් අගය, ඒකක දුරකට තිබෙන හායනය, කේබලය හරහා යැවිය හැකි උපරිම සංඥා වෝල්ටියතාව/ජවය යන කරුණු මත මෙම කේබල් වර්ගීකරණය කර ඇත. කේබලයේ ඇති සන්නායකවල ගේජ් එක වැඩි වන විට හායනය අඩු වන අතර පවර් රේටිං එක වැඩි වේ. කේබලයේ ගේජ් එක වැඩි වන විට මිලද වැඩි වේ. කේබලය හරහා ගමන් කරන සංඥාවේ සංඛ්‍යාතය වැඩි වන විට ලොස් එක වැඩි වන අතර (බලන්න තෙවන හා සිව්වැනි තීරු දෙක), පවර් රේටිං එකද අඩු කළ යුතුය (මේ දෙකටම හේතුව චර්මීය ආචරණයයි).

පහත දැක්වෙන්නේ එවැනි කොඇක්ස් කේබල් කිහිපයක විස්තර සාරාංශයයි. මෙහි ලොස් අගයන් අඩි 100ක් සඳහා ඩෙසිබල්වලින් ප්‍රකාශ කර තිබේ. සංඛ්‍යාතයන් කිහිපයක් සඳහාම ලොස් එකේ දළ සංඛ්‍යාත්මක අගයන් පෙන්වා ඇත. ඇත්තටම මීට පෙර ඉතා විශාල සංඛ්‍යාත පරාසයක් සඳහා ලොස් එක කේබල් වර්ග රාශියක් සන්තතිකව විචලනය වන අයුරු ප්‍රස්ථාරයකින්ද පෙන්වා දුන්නා.

Type	Z0	Loss @ 30MHz	Loss @ 100MHz	Loss @ 150MHz	Loss @ 400MHz	VF	Vmax (rms)
RG-6/U	75	1.4	2.3	3.3	4.7	0.75	2700
RG-8/U	50	1.1	1.9	2.5	4.5	0.75	4000
RG-8X	50	2.0	3.7	4.5	8.0	0.75
RG-58/U	50	2.5	4.3	5.6	9.4	0.66	1900
RG-59/U	75	1.8	2.9	4.1	5.9	0.66	2300
RG-174	50	4.6		10.3		0.66
RG-213	50	1.1	1.9	2.5	4.1	0.66	5000

RG යනු Radio Guide යන්නෙහි කෙටි වචනයයි. ඇත්තටම එය පැරණි ප්‍රමිතියක් වුවද, අදටත් එම නමින් කේබල් වර්ග වෙළඳපොලේ ඉතා ජනප්‍රියව ඇත. එනිසා RG යනු යම් කොම්පැනියකින් සාදන කේබල් වර්ගයක් නොව; එය පොදු ප්‍රමිතියකි. RG ට පසුව යම් සංඛ්‍යාවක් ඇත. සමහරවිට ඊට පිටුපසින් /U තිබිය හැකියි. එහි තේරුම universal යන්නයි (එනම් සාමාන්‍ය භාවිතයට සුදුසු යනුයි).

සමහර කොඇක්සියල් කේබල්වල මැද සන්නායකය තනි කම්බියක් (solid conductor) වෙනුවට ඇත්තේ කම්බි කෙඳි ගණනාවකි (stranded conductor). තනි කම්බියේ ප්‍රතිරෝධය කෙඳි සමූහයේ ප්‍රතිරෝධයට වඩා අඩුයි RF වලදී. කෙඳි ආකාරයේ සන්නායකයක තිබෙන වාසිය තමයි පහසුවෙන් කේබලය නැමීමට ඇති හැකියාව (flexible).

තවද, කොඇක්සියල් කේබලයේ වටේට ඇති සන්නායක කොටස (shield) දෙයාකාරයකින් තිබිය හැකිය. එකක් නම්, සිහින් කම්බි ජාලාවක් (braid) ලෙස වන අතර අනෙක තනි සිහින් තහඩුවක් ලෙසයි. තනි තහඩුවක් සේ ෂීල්ඩ් ඇති කේබල්වල හායනය අඩුය (ප්‍රතිරෝධය අඩුය). බ්‍රේඩ් එක හා තනි තහඩුව යන දෙකම එකට තිබෙන උසස් ගණයේ කේබල්ද ඇත.

කේබලය හරහා ගමන් කළ හැකි සංඛ්‍යාත පරාසයක් තිබෙන බව කිහිප සැරයක්ම මා පවසා තිබෙනවා. ඊට එක් හේතුවක් නම් චර්මීය ආචරණයයි. අනෙක් හේතුව transverse mode යනුවෙන් හඳුන්වනු ලබන තත්වයයි. සංඥාවක විදුලි හා චුම්භක යන ක්ෂේත්‍ර දෙකක් තිබෙනවානෙ. මෙම ක්ෂේත්‍ර දෙක දී තිබෙන මාධ්‍යය තුල ගමන් කරන්නේ (පිහිටා තිබෙන්නේ) කෙසේද යන්න මත ට්‍රාන්ස්වර්ස් මෝඩ් එක කුමක්ද යන්න තීරණය වේ.

.

සාමාන්‍යයෙන් කොඇක්සියල් කේබලයක් හරහා සංඥා ගමන් කරන්නේ Transverse ElectroMagnetic (TEM) යන ආකාරයෙන්. සංඛ්‍යාතය හර්ට්ස් 0 (හර්ට්ස් 0 යනු DC යන්නයි) සිට ඉතා විශාල හර්ට්ස් ගණනක් (VHF හෝ UHF කලාපයේ සංඛ්‍යාතයක්) දක්වා පුලුලු පරාසයක සංඛ්‍යාත මේ ක්‍රමයෙන් ගමන් කරයි. මෙම උපරිම සංඛ්‍යාතය cut-off frequency ලෙස හඳුන්වමු. ඇත්තටම ටෙම් ක්‍රමයෙන් කට්ඕෆ් සංඛ්‍යාතයටත් වඩා වැඩි සංඛ්‍යාත ගමන් කරනවා. එහෙත් එම කට්ඕෆ් සංඛ්‍යාතය ඇරඹෙන සංඛ්‍යාතයේ සිට තවත් ට්‍රාන්ස්වර්ස් මෝඩ් එකකින් (Transverse Electric – TE₁₁ ලෙස මෙම මෝඩ් එක හැඳින්වේ) සංඥා ගමන් කිරීම ඇරඹෙනවා. මෙවිට එකම සංඥාවේ කොපි දෙකක් මෝඩ් දෙකකින් යෑම නිසා සංඥා විකෘතියක් ඇති විය හැකිය. අන්න එම හේතුව නිසයි කට්ඕෆ් සංඛ්‍යාතය උපරිම සංඥා සංඛ්‍යාතය ලෙස සැලකීමට සිදු වන්නේ.

යම් කොඇක්සියල් කේබලයක සන්නායක කොටස්වල විශ්කම්භ අගයන් දන්නවා නම් ඉතාම පහසුවෙන් කට්ඕෆ් සංඛ්‍යාතය දළ වශයෙන් සෙවිය හැකිය. TE₁₁ මෝඩ් එකේදී කේබලයේ පරිධිය (“වෘත්තයක පරිධිය = π x විශ්කම්භය” වේ) වටේට තනි සංඥාවක් පිහිටිය යුතුය. ඒ කියන්නේ කේබලයේ පරිධියේ දිගට සමාන දිගක් තිබෙනවා එය වටේට ගමන් කරන සංඥාවේ තරංග ආයාමයට (පරිධිය = තරංග ආයාමය).

දැන් කේබලයේ හරස්කඩ පරිධිය ගණනය කිරීම සඳහා යෙදිය යුතු විශ්කම්භ අගය කුමක් විය යුතුද? සංඥාව (ඇත්තටම සංඥාවේ ක්ෂේත්‍ර) ගමන් කරන්නේ ඩයිඉලෙක්ට්‍රික් එක තුලින්ය. එනිසා ඩයිඉලෙක්ට්‍රික් එකෙහි මැද ගත යුතුය. එම මැද අගය වන්නේ කොඇක්සියල් කේබලයේ මැද කම්බියේ පිටත විශ්කම්භ අගය (d1) හා ෂීල්ඩ් එකේ ඇතුලත විශ්කම්භ අගය (d2) ගෙන, එම අගයන් දෙක එකට එකතු කර, 2න් බෙදූ විට ලැබෙන අගයයි. දැන් අපට හැකියි සූත්‍රය පහත ආකාරයට ව්‍යුත්පන්න කරන්නට. ඒ අනුව යම් කොඇක්සියල් කේබලයක් හර්ට්ස් 0 සිට f_cutoff දක්වා වූ සංඛ්‍යාත පරාසය සපෝට් කරනවා. ප්‍රායෝගිකම මෙම අගයෙන් 90%ක පමණ අගය කට්ඕෆ් අගය ලෙස සලකනවා (safety factor).

කොඇක්සියල් කේබලයක් හරහා ගමන් කරන සංඥාවක තිබිය හැකි උපරිම ජව හෝ වෝල්ටියතා හෝ ධාරා අගයක් තිබෙනවා. එය තීරණය කරන සාධක දෙකකි. එකක් නම් කේබලයේ ඇති සන්නායක ඔස්සේ ධාරාවක් ගමන් කරන විට ඉන් ඇති වන තාපයයි. මෙම සාධකය සෑම සන්නායකයකටම පොදුය. එනිසා සාමාන්‍ය AWG හෝ SWG වගුවකින් එක් එක් කම්බි ගනකමට අදාල මෙම උපරිම ධාරා අගයන් සොයා ගත හැකිය. එහෙත් විදුලි කම්බි දෙකක් ඩයිඉලෙක්ට්‍රික් එකකින් වෙන් කර තිබෙන විට තවත් සාධකයක් බලපානවා. ඇත්තටම එවිට තීරණාත්මක සාධකය වන්නේද එයයි. එය තමයි ඩයිඉලෙක්ට්‍රික් එකේ breakdown voltage හෙවත් dielectric strength යන අගය.

කොඇක්සියල් කේබල්වල භාවිතා වන ඩයිඉලෙක්ට්‍රික් කිහිපයක බ්‍රේක්ඩවුන් වෝල්ටියතාවන් බලමු. PE සඳහා මීටරයට කිලෝවෝල්ට් 200ත් 300ත් අතර වේ. ටෙෆ්ලෝන් සඳහා එම අගය 600ත් 700ත් අතර වේ. වාතයේ අගය මීටරට කිලෝවෝල්ට් 15ත් 30ත් අතර වේ. pvc සඳහා 140ත් 200ත් අතර වේ.

ඔබ දන්නවා කොඇක්සියල් කේබලයේ මැද කම්බිය හා වටේ ෂීල්ඩ් එක අතර තුනී ඩයිඉලෙක්ට්‍රික් එකක් තිබෙනවා. මෙම ඩයිඉලෙක්ට්‍රික් එකේ පරිවාරක ගුණය නැති වී සන්නායකයක් බවට පත් වෙනවා යම් උපරිම වෝල්ටියතාවකට වඩා වැඩි වූ විට (එනම් එම ඩයිඉලෙක්ට්‍රික් එකේ බ්‍රේක්ඩවුන් වෝල්ටියතාවට වඩා වැඩි වූ විට). එවිට කේබලය ෂෝට් වේවි. සාමාන්‍යයෙන් ඩයිඉලෙක්ට්‍රික් ස්ට්‍රෙන්ත් අගය සලකා බලනු ලබන ඩයිඉලෙක්ට්‍රික් එකේ මීටරයක ගනකමක් සඳහා කොච්චරද යනුවෙන් ලබා දුන්නත්, ගණනය කිරීමේදී එතැන තිබෙන සත්‍ය ගනකමයි වැදගත් වන්නේ. උදාහරණයක් ලෙස, යම් ඩයිඉලෙක්ට්‍රික් එකක බ්‍රේක්ඩවුන් වෝල්ටියතාව මීටරයට වෝල්ට් 100,000 ලෙස ඇති විට, සෙන්ටිමීටරයක ගනකමකදී එය වෝල්ට් 1000 වේ. එනිසා ප්‍රායෝගිකව යොදා ගන්නේ කුඩා ගනකම් සහිත ඩයිඉලෙක්ට්‍රික් නිසා, මෙම සාධකය ප්‍රමුඛවන බව දැන් පැහැදිලියිනෙ.

මෙම උපරිම වෝල්ටියතාව සොයන සූත්‍රය පහත ඇත. මෙහි d1 හා d2 අගයන් ඇත්තටම ඩයිඉලෙක්ට්‍රික් කොටසටයි අදාල වන්නේ. මෙහිදී d1 යනු මැද කම්බියේ පිටත විශ්කම්භ අගයයි (පෙර සූත්‍රයේ මෙන්ම). මැද කම්බියේ පිටත විශ්කම්භය යනු ඩයිඉලෙක්ට්‍රික් එකේ ඇතුලත විශ්කම්භය කියන එකමයිනෙ. එලෙසම, d2 යනු ෂීල්ඩ් එකේ ඇතුලත විශ්කම්භය වේ. එය ඩයිඉලෙක්ට්‍රික් එකේ පිටත විශ්කමභයම නේද?

ප්‍රායෝගිකව මෙලෙස ලැබෙන උපරිම වෝල්ටියතා අගයෙන් 1/10 ක පමණ අගයකුයි ගන්නේ (safety factor); මෙම 1/10 ක් ලෙස ගත් අගයයි වගුවල සටහන් කරන්නේ (අවසාන අගය ලෙස). ඊට හේතුව විදුලියේ ස්වභාවය (සංඛ්‍යාතය වැනි), හා වෙනත් ප්‍රායෝගිකව ඇතිවන අවිනිශ්චිත තත්වයන් අනුව මෙම අගය විචලනය වේ. උදාහරණයක් ලෙස, ඉහත සූත්‍රයෙන් ලැබෙන අගය වලංගු වන්නේ කේබලය හරහා ඇන්ටනාව දෙසට යන සම්පූර්ණ සංඥාව (හෝ ඉන් ඉතාම වැඩි කොටසක්) ඇන්ටනාව විසින් උරා ගන්නා අවස්ථාව සඳහාය (එනම් විස්වර් අගය අඩු විටයි). එහෙත් ආපස්සට සංඥා පරාවර්තනය වන විට දැන් කේබලය මත වැඩිපුර වෝල්ටියතාවක් පැවතිය හැකියි. එනිසා සේෆ්ටි ෆැක්ටර් එකේ වැදගත්කම ඉතා ඉහලය.

අවශ්‍ය නම් දැන් අපට පුලුවන් මෙම අවසාන උපරිම වෝල්ටියතා අගයන් උපරිම ජව අගයක් බවට පත් කර ගන්නට. ප්‍රතිරෝධ අගය ලෙස ගන්නේ කේබලයේ කැරක්ටරිස්ටික් ඉම්පීඩන්ස් අගය වේ. එවිට කේබලයක් සපෝට් කරන උපරිම ජවය සොයන සූත්‍රය පහත ආකාරයට ලැබේ.

Power_peak = V²_peak/(2Z₀)

ඉහත සූත්‍රයම තවත් සුලු කර (එනම් කැරක්ටරිස්ටික් ඉම්පීඩන්ස් අගයට අදාල සූත්‍රයක් ආදේශ කර), පහත ආකාරයටද උපරිම ජවය සොයන සූත්‍රයක් සාදා ගත හැකියි. මතක තබා ගන්න ජවය සොයන මෙම සූත්‍ර දෙකද විස්වර් අගය අඩු තත්වයන්වලටයි සාමාන්‍යයෙන් වලංගු වන්නේ (මොකද ජවය සොයන්නේ පෙර සොයා ගත් උපරිම වෝල්ටියතාව මතයි; එම උපරිම වෝල්ටියතාව විස්වර් අගය මත වෙනස් වන බව පැවසුවනෙ). එසේ වුවත්, සේෆ්ටි ෆැක්ටර් එක නිසා තිබෙන අවිනිශ්චිත බවට ඔරොත්තු දීමේ හැකියාවක් තිබෙනවා.