අතාත්වික සංඛ්යා (imaginary numbers)
නැවතත්
ඉහත සලකා බැලූ එහෙත් විසඳීමට
අපහසු ගණිත ගැටලුව බලමු.
-4 හි වර්ගමූලයයි
සොයන්නට තිබෙන්නේ. -4 යන
සංඛ්යාව -1x4 ලෙස
ලිවිය හැකියි නේද? එවිට
පහත ආකාරයට තරමක් දුරට එම
ගැටලුව සුලු කරගෙන යා හැකියි.
මෙහිදී
කිසිසේත් සුලු කර ගත නොහැකි
වූ විශාල තනි සංඛ්යාව තරමක්
දුරට සුලු කර ගත හැකි වෙනවා.
දැන් සුලු
කර ගැනීමට බැරි කොටස වන්නේ
-1හි
වර්ගමූල පදයයි. මෙයත්
තරමක ජයග්රහණයකි.
මේ
ආකාරයට ඕනෑම ඍණ සංඛ්යාවක
වර්ගමූලය ඉහත පෙන්වූ විදියට
සුලු කර ගත හැකියි. එවිට
-1හි
වර්ගමූල පදයක් සුලු කර ගත
නොහැකිව ඉතිරි වේ. ඇත්තටම
කිසිම කෙනෙකු අදටත් දන්නේ
නැහැ මෙම -1 හි
වර්ගමූලය විසඳන අයුරු.
තවද,
මෙම -1
හි වර්ගමූලය
විසඳන තුරු තවමත් විශාල
ප්රකාශයට හරි නිවැරදි හැඟීමක්
ලැබෙන්නේද නැත. ඒ
කියන්නේ -4හි
වර්ගමූල පදයේ සත්ය වටිනාකම/අගය
කුමක්දැයි තවම අපට සිතා ගත
නොහැකියි.
-1හි
වර්ගමූලය ලිවීම තවදුරටත්
පහසු කිරීමට “-1හි
වර්ගමූලය" වෙනුවට
i
යන ඉංග්රිසි
අකුර ආදේශ කරන්නට සම්මත කරගෙන
ඇත. ඒ
අනුව:
මෙලෙස
i අකුරක්
සහිත සංඛ්යා අලුත් සංඛ්යා
වර්ගයක් ලෙස සැලකීමට සම්මත
කරගෙන ඇත.
මීට
හේතුව -1හි
වර්ගමූලයේ සත්ය තේරුම/වටිනාකම
අපට සිතා ගත නොහැකි වීමයි.
මෙවිට
තිබෙන හොඳ ප්රායෝගික විසඳුම
වන්නේ අලුත් ජාතියක අගයක්/සංඛ්යාවක්
ලෙස එය සැලකීමයි.
මෙම
අමුතු ජාතියේ සංඛ්යා අතාත්වික
සංඛ්යා (imaginary
numbers) ලෙස
හැඳින්වෙනවා.
අතාත්වික
යන්නෙහි තේරුම "තාත්වික
නොවන"
හෙවත්
"සත්ය
ලෙසම නොපවතින"
යන්නයි.
එම
යෙදුම සාධාරණයි නේද?
-1 හි
වර්ගමූල පදයේ හෙවත් i
පදයේ
තේරුම/අගය
හරියටම අප දන්නේ නැත.
තවද
මෙම අතාත්වික සංඛ්යා කිසිසේත්
තාත්වික සංඛ්යා ගොඩට දැමිය
නොහැකියි.
ඇත්තටම
අතාත්වික සංඛ්යා ලෙස මෙලෙස
සංඛ්යා වර්ගයක් සම්මත කර
ගැනීමට අවශ්යතාවක් මතු වෙන්නේ
මෙවැනි සංඛ්යාවලින් යම්
ප්රයෝජන ගත හැකි නම්ය.
ප්රයෝජනයක්
නැති කොතෙකුත් දේවල් සම්මත
කර ගත හැකිය.
එහෙත්
වැඩක් නැත.
අතාත්වික
සංඛ්යාවල ප්රයෝජන (applications)
ඇත.
එනිසා
අතාත්වික සංඛ්යා ගැන ඉගෙනීමට
අවශ්ය වේ.
ධන
සංඛ්යාවකින් ඍණ සංඛ්යාවක්
වෙන් කොට හඳුනා ගන්නේ ඍණ
සංඛ්යාවට ඉදිරියෙන් තිබෙන
- යන
සංඛේතය නිසාය.
එලෙසම
සාමාන්ය තාත්වික සංඛ්යාවකින්
අතාත්වික සංඛ්යාවක් වෙන්
කොට හඳුනාගන්නේ සංඛ්යාවට
ඉදිරියෙන් හෝ පිටුපසින් i
අකුරක්
යෙදීමෙනි.
අතාත්වික
සංඛ්යාද ඍණ අනන්තයේ සිට ධන
අනන්තය දක්වා පරාසයක විහිදී
පවතී.
තවද,
පූර්ණ
අතාත්වික සංඛ්යා මෙන්ම
දශම/භාග
අතාත්වික සංඛ්යාද පවතිනවා.
පරිමේය
අපරිමේය යන භේදයත් මෙම සංඛ්යාවල
පවතිනවා.
ඔත්තේ
ඉරට්ටේ යන භේදයද පවතිනවා.
මෙලෙස
තාත්වික සංඛ්යාවල තිබූ සියලු
භේදයන් අතාත්වික සංඛ්යාවල
පවතිනවා.
මීට
අමතරව ශූන්යයද (0i)
මෙහි
පවතිනවා.
තාත්වික
සංඛ්යාවලට තාත්වික සංඛ්යා
රේඛාවක් තිබෙන්නා සේම,
අතාත්වික
සංඛ්යාවලටද අතාත්වික සංඛ්යා
රේඛාවක් පවතිනවා.
තාත්වික
සංඛ්යා රේඛාව තිරස්ව අඳිනු
ලබන අතර,
අතාත්වික
සංඛ්යා රේඛාව සිරස්ව අඳිනු
ලබනවා.
සියලුම
අතාත්වික සංඛ්යා මෙම අතාත්වික
සංඛ්යා රේඛාව මත නිරූපණය කළ
හැකියි.
ඇත්තටම
0i යන්න
තාත්වික සංඛ්යාවල පවතින
සාමාන්ය 0ට
සර්වප්රකාරයෙන්ම සමානයි.
ඒ
කියන්නේ තාත්වික හා අතාත්වික
යන සංඛ්යා වර්ග දෙකෙහිම පවතින
ශූන්යයන් දෙකම එකිනෙකට
සමානයි.
මෙය
සුවිශේෂි අවස්ථාවකි.
මෙම
තත්වයත් ඔබට පහසුවෙන් තේරුම්ගත
හැකියි.
තාත්වික
හෝ අතාත්වික හෝ වෙනත් ඕනෑම
ආකාරයක ශූන්යය යනු කිසිත්
නොමැති අවස්ථාවයි.
උපමාවකින්
එය තවදුරටත් බලමු.
යම්
බෝතලයක ඇත්තේ වතුර යැයි සිතන්න.
දැන්
එම වතුර ටික ඉවත් කළ විට,
බෝතලය
"ශූන්ය"
වේ
(රික්තකයක්
බවට පත් වේ).
දැන්
එම බෝතලයම පොල් තෙල්වලින්
පුරවා ඇතැයි සිතමු.
එම
තෙල් බෝතලයෙන් ඉවත් කළ විට
නැවත බෝතලය "ශූන්ය"
වේ.
මේ
ආකාර දෙකෙන්ම ලැබුණු "ශූන්යබව"
සර්වප්රකාරයෙන්ම
සමානයි නේද?
තාත්වික
සංඛ්යා හා අතාත්වික සංඛ්යා
යනු එකිනෙකට වෙනස් සංඛ්යා
කාණ්ඩ දෙකක් බව පෙරත් පැවසුවා.
එහෙත්
පෙර මතු කළ තර්කය අනුව,
මෙම
සංඛ්යා කාණ්ඩ දෙකටම පොදු
එකම සංඛ්යාව/අගය
0 වේ.
මෙම
හේතුව නිසා පහත ආකාරයට තාත්වික
හා අතාත්වික යන සංඛ්යා රේඛා
දෙකම එකට ඇඳිය හැකියි (මේ
දෙකටම 0
පොදු
නිසා,
රේඛා
දෙක 0 දී
එකිනෙකට ඡේදනය වේ).
අතාත්වික
සංඛ්යාවලටද සුපුරුදු ගණිත
කර්ම සියල්ලම සිදු කර ගත හැකියි.
අතාත්වික
සංඛ්යා තවත් අතාත්වික සංඛ්යා
සමග සිදු කරන ගණිත කර්ම ගැන
සොයා බලමු.
අතාත්වික සංඛ්යා එකතු කිරීම හා අඩු කිරීම
සාමාන්යයෙන්
තාත්වික සංඛ්යා එකතු කිරීමේදී
පිළිපැද්ද රීතින් එලෙසම
පිළිපදින්න.
අමුතුවෙන්
ඉගෙනීමට දෙයක් මෙහි නැත.
1.
4i + 3i = 7i
2.
1i + 0i = 1i
3.
23.5i + 10.12i = 33.62i
4.
5i – 2i = 3i
5.
51.43i – 0.2i = 51.23i
6.
3i – 5i = -2i
7.
2i + (-3i) = -1i = -i
8.
(-4i) + (-i) = -5i
අතාත්වික සංඛ්යා දෙකක් ගුණ කිරීම හා බෙදීම
අතාත්වික
සංඛ්යා දෙකක් ගුණ කරන විට
හා බෙදන විට
කරුණු දෙකක් පිළිපදින්න.
1.
තාත්වික
සංඛ්යාවල පිළිපැද්ද "ධනයි
ධනයි හෝ ඍණයි ඍණයි වැඩි කළ විට
(හෝ
බෙදූ විට)
ධන,
හා
ධනයි ඍණයි වැඩි කළ විට (හෝ
බෙදූ විට)
ඍණද
ලැබේ"
යන
සුපුරුදු රීතිය පිළිපදන්න.
"සමාන
ලකුණු වැඩි කළ විට ධනද,
අසමාන
ලකුණු වැඩි කළ විට ඍනද ලැබේ"
යනුවෙන්ද
මෙම රීතිය මතක තබා ගත හැකියි.
එහෙත්
පහත දෙවැනි රීතිය නිසා,
ගුණ
කිරීමෙන් ලැබෙන -1න්
හා බෙදීමෙන් ලැබෙන +1න්
අවසාන පිළිතුර නැවත ගුණ වෙන
බවද මතක තබා ගන්න.
2.
තාත්වික
සංඛ්යා දෙකක් ගුණ කළ විට හෝ
බෙදූ විට ලැබෙන පිළිතුර හැමවිටම
තාත්වික සංඛ්යාවකි.
ඇත්තටම
මෙය නම් ඉතාම අපූරු ප්රතිඵලයක්.
එහෙත්
මෙසේ සිදු වීම හාස්කමක් නොවේ.
එය
සිදු වන්නේ පහත ආකාරයේ සාමාන්ය
සුලු වීමක් එහි
සිදුවන නිසාය.
උදාහරණ
ලෙස;
1. 5i x 4i = 5x4i2
= 20x(-1) = -20
2. 2i x 0i = 2i x 0
(හෝ 0i2)=
0i (හෝ 0
x -1) = 0
3. 3i x -3i = -9i2
= -9 x -1 = 9
4. -5i x -3i = 15i2
= 15 x -1 = -15
5. 4i / 2i = 2
6. 5i/2i = 2.5
7. -6i/3i = -2
8. -8i/-2i = 4
අතාත්වික සංඛ්යාවක හා තාත්වික සංඛ්යාවක ගුණ කිරීම හා බෙදීම
අතාත්වික
සංඛ්යාවක් තාත්වික සංඛ්යාවකින්
ගුණ කරන විට හෝ බෙදන විට,
i අකුර නැතැයි
සිතාගෙන එය සිදු කරන්න;
පිළිතුර
අගට ඉන්පසු i දමන්න.
උදාහරණ:
1. 4i / 2 = 2i
2. -6i / 3 = -2i
3. -5i/-2 = 2.5i
4. 4i x 2 = 8i
5. -3i x -3 = 9i
අතාත්වික
සංඛ්යාවක් භාග සංඛ්යාවේ
හරය ලෙස පවතින විටද සාමාන්ය
සුලු කිරීමේ ක්රම ඔස්සේ සුලු
කළ හැකියි. උදාහරණයක්
4/2i සුලු
කරන හැටි බලමු.
පළමුව
හරයේ තිබෙන i පදය
ඉවත් කළ යුතුය. එය
කිරීමට හරය හා ලවය යන දෙකම i
වලින් ගුණ
කරන්න. එවිට
හරයේ තිබෙන i ලවයට
යයි (ඍණ
ලකුණකුත් සමග). ඉන්පසු
සාමාන්ය පරිදි සුලු කරන්න.
ඇත්තටම
ඉහත ආකාරයට දීර්ඝ ලෙස සුලු
කරන්නේ නැතිව කෙටි ක්රමයට
මෙසේ එය සිදු කළ හැකියි.
භාගයක හරයේ
(යට
කොටසේ) i පදයක්
ඇති විට, එම
i ලවයට
ගෙන යන්න; එවිට
එය -i ලෙස
ළවයේ ලියන්න. උදාහරණයක්
ලෙස ඉහත උදාහරණයම කෙටියෙන්
මෙසේ සුලු කළ හැකියි.
4/2i = 4(-i)/2 =
-4i/2 = -2i
මෙතෙක්
උගත් කරුණු එකට යොදා ගෙන
විවිධාකාරයේ සුලු කිරීම් කළ
හැකියි. උදාහරණ
කිහිපයක් බලමු.
1. 4i x 2i x 3i =
(4i x 2i) x 3i = -8 x 3i = -24i හෝ
24i3 = 24 x (i2 x I) = 24 x -1 x
i = -24i
2. 6i x 3i / 9i =
18i2/9i = -18/9i = (-18 x -i)/9 = 18i/9 = 2i
තාත්වික
සංඛ්යාවක් හා අතාත්වික
සංඛ්යාවක් සමග ගුණ කරන හා
බෙදන අයුරු දැන් ඔබ දන්නවා.
තාත්වික
සංඛ්යාවක් හා අතාත්වික
සංඛ්යාවක් එකට එකතු කිරීම
හා අඩු කිරීම සිදු කරන්නේ
කෙලෙසද? තාත්වික
සංඛ්යා එකිනෙකට ගණිත කර්මවලට
ලක් කරන විට, අවසානයේ
තනි පිළිතුරක් ලැබුණි.
එලෙසම අතාත්වික
සංඛ්යා දෙකක් එකිනෙකට ගණිත
කර්මවලට ලක් කරන විට,
අවසානයේ
තනි පිළිතුරක් ලැබුණි.
තවද,
තාත්වික හා
අතාත්වික සංඛ්යා දෙකක්
එකිනෙකට ගුණ කරන විට හා බෙදන
විට, අවසානයේ
තනි පිළිතුරක් ලැබුණි.
එහෙත් තාත්වික
හා අතාත්වික සංඛ්යා දෙකක්
එකතු කරන විට හා අඩු කරන විට,
අවසානයේ
තනි තාත්වික හෝ අතාත්වික
සංඛ්යාවක් ලැබෙන්නේ නැත.
ඒ වෙනුවට
ලැබෙන්නේ සංකීර්ණ සංඛ්යාවකි
(complex number).



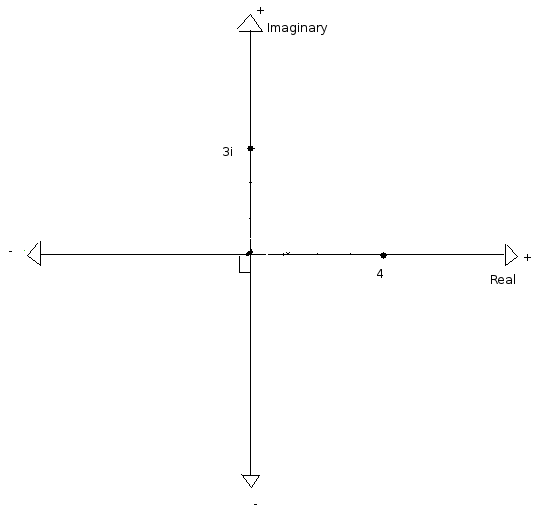


Comments
Post a Comment
Thanks for the comment made on blog.tekcroach.top