දැන්
අපි ඩිජිටල් මූර්ජන ක්රම
ගැන සොයා බලමු.
රේඩියෝ
තරංග ඔස්සේ ඩිජිටල් සංඥා
විසුරුවාලන්නට පෙර එම ඩිජිටල්
දත්ත මූර්ජනයට ලක් කළ යුතු
බව ඔබ දැන් දන්නවා.
තවද,
රේඩියෝ
තරංග මඟින් නොව,
කේබල්/වයර්
තුලින් දිගු දුරකට ඩිජිටල්
සංඥා යවන විටත් මූර්ජනයේ
අවශ්යතාව තිබෙනවා.
මූර්ජනය
අත්යවශ්ය නොවන්නේ බේස්බෑන්ඩ්
ආකාරයට ඩිජිටල් (හෝ
ඇනලොග් වුවද)
සංඥා යවන
විටයි (සාමාන්ය
සර්කිට් බෝඩ්වල ඩිජිටල් සංඥා
යන්නේ බේස්බෑන්ඩ් ක්රමයටනෙ).
සාමාන්යයෙන්
සංඥා විසුරුවා හැරීමට යම්
මාධ්යයක් තෝරා ගැනීමේදී එම
මාධ්යය වඩා සුදුසු ඇනලොග්
සංඥා සඳහාද ඩිජිටල් සංඥා සඳහාද
යන්නත් වැදගත් වෙනවා.
උදාහරණක්
ලෙස,
සාමාන්ය
රැහැන් දුරකතනවල යොදා තිබෙන
රැහැන්/වයර්
සාදා තිබෙන්නේම ඇනලොග් සංඥා
යැවීමටයි.
රේඩියෝ
තරංග ස්වභාවයෙන්ම සුදුසු
වන්නේ ඇනලොග් සංඥා සඳහාය.
ඇත්තටම
බොහෝ මාධ්ය ඇනලොග් සංඥා
සඳහායි ස්වභාවයෙන්ම සැදී
පැහැදී සිටින්නේ.
එහි අරුමයක්
නැත මොකද ස්වාභාවික ලෝකය මෙන්ම
එහි සංසිද්ධි ඇනලොග්ය.
ඉතිං
එවැනි “ඇනලොග් මාධ්යයක්”
හරහා ඩිජිටල් සංඥා යැවිය
හැකිද?
ඔව්,
කොන්දේසිවලට
යටත්ව හැකියි.
එහි ක්රම
දෙකක් අනුගමනය කළ හැකියි -
conversion හා
modulation.
එකක්
නම්, ඩිජිටල්
සංඥාව DAC
(Digital-to-Analog Converter) එකක්
හරහා යවා පළමුව එම ඩිජිටල්
සංඥාව ඇනලොග් සංඥාවක් බවට
පත් කර,
එම ඇනලොග්
සංඥාව යැවිය හැකියි.
එහෙත්
එම conversion
ක්රමය
හොඳ ක්රමයක් නොවේ.
එහි අමතරව
DAC (හා
ආදායකයේදී ADC)
උපාංග
භාවිතා කිරීමට සිදු වන අතර
අමතර වියදමක් ඒ සඳහා වැය වේ.
සංකීර්ණතාවද
වැඩි වේ.
ඊටත් වඩා,
ඩිජිටල්
සංඥාවල තිබූ සියලු හොඳ
ගතිගුණ/ලක්ෂණ
අපට අහිමි වේ.
එනිසා
මේ ක්රමය භාවිතා නොවේ.
දෙවැනි
ක්රමය ඉහතදී හමු වූ ගැටලු
නැති ඉතා හොඳම ක්රමයයි.
එහිදීත්
ඩිජිටල් සංඥා (කොටු
හැඩැති සංඥා)
ඇනලොග්
සංඥා (සයිනාකාර
හැඩැති)
බවට පත්
කරයි.
එහෙත්
මෙහිදී එය සිදු කරන්නේ DAC
(හා ADC)
උපාංග
භාවිතා කරන්නේ නැතිව,
මූර්ජක
(හා
විමූර්ජක)
පරිපථ
භාවිතයෙනි.
එනිසා
මෙහිදී conversion
වෙනුවට
සිදු වන්නේ modulation
එකකි.
මේ ක්රමයෙන්
ඩිජිටල් සංඥාවක් ඊට අනුරූප
ඇනලොග් සංඥාවක් බවට පත් කිරීම
modulation ලෙසද,
අනෙක්
කෙලවරේදී (එනම්
ආදායකයේදී)
එම ඇනලොග්
සංඥාව නැවත මුලින් තිබූ ඩිජිටල්
සංඥාව බවට පත් කිරීම demodulation
ලෙසද
හඳුන්වනවා.
ඇත්තටම
ඩිජිටල් සංඥා මූර්ජනයත් මීට
පෙර අප උගත් ඇනලොග් සංඥා
මූර්ජනයේම විශේෂ අවස්ථාවක්
ලෙසත් සැලකිය හැකියි (මොහොතකින්
ඒ ගැන විස්තරාත්මකව බලමු).
එනිසයි
modulation හා
demodulation යන
වචන දෙක මෙහි භාවිතා වෙන්නේ.
මෙම
ක්රමයේදී ඩිජිටල් සංඥා දෙක
වන 1 හා
0, යම්
කිසි ක්රමයකින් වාහක තරංගයේ
යම් ගති ගුණයක් වෙනස් කිරීම
මඟින් “නියෝජනය” වෙනවා.
උදාහරණයක්
ලෙස, ඩිජිටල්
1 සංඥාව
වාහකයේ විස්තාර අගය වෝල්ට්
3කින්ද,
ඩිජිටල්
0 සංඥාව
එම වාහකයේම විස්තාර අගය වෝල්ට්
1කින්ද
නියෝජනය කළ හැකියි (මෙලස
වාහකයේ විස්තාර අගය 1
හා 0
අනුව
මට්ටම් දෙකක් මඟින් නිරූපණය
කරන මූර්ජන ක්රමය ASK
වේ).
මෙය
පැහැදිලිවම සංඥා පරිවර්තන
(conversion)
ක්රියාවක්
නොව, යම්
භෞතික ස්වරූපයකින් පවතින එක්
සංඥාවක් තවත් ස්වරූපයක සංඥාවකට
ගැලපීමක් හෙවත් match
කිරීමකි
(mapping,
representing, associating යන
වචනද මේ සඳහා සුදුසුය).
උපමාවකින්
කියතොත්,
වම් අත
ඉස්සුවොත් 0
ද,
දකුණු
අත ඉස්සුවොත් 1ද
ලෙස තේරුම් ගන්න කියා දෙන
උපදෙසක් වැනිය.
අත හා
ඩිජිටල් සංඥා අතර කිසිදු
ඓන්ද්රිය සම්බන්ධයක් නැතත්,
සම්මුතියකින්
ඒ දෙක අතර ඉහත කියූ ලෙස සම්බන්දතාවක්
ගොඩනැගිය හැකියිනෙ.
ඩිජිටල්
මූර්ජනයෙන් අපට ලැබෙන ඇනලොග්
සංඥාවේ යම් ක්රමවත් බවක්
(එනම්
ඩිජිටල් ගතිය)
තිබේ.
අවසානයේ
ලැබෙන්නේ ඇනලොග් සංඥාවක්
වුවත්,
එම ඇනලොග්
සංඥාව හැමවිටම පවතින්නේ
තත්වයන් (එනම්
විස්තාර අගයන් හෝ සංඛ්යාත
හෝ කලා අගයන්)
දෙකක්
අතරය. පහත
රූපයේ ඒ බව පැහැදිලිවම දක්වා
ඇත. ඇනලොග්
වුවත්,
විචලනය
තත්වයන් දෙකක් අතරේ පමණක්
පවතින නිසා ඩිජිටල් ගතිය එහි
පවතින බව පෙනේ.
එනිසා
විමූර්ජක පරිපථයට යම් පහසුවක්
තිබෙනවා සංඥා නිවැරදිව
හඳුනාගැනීමට.
ඒ කියන්නේ
ඝෝෂාවට හොඳින් ඔරොත්තු දීමේ
හැකියාව පවතිනවා.
දැන්
ප්රශ්නය වන්නේ ඇනලොග් සංඥාත්
විද්යුත් සංඥා නම්,
ඩිජිටල්
සංඥාත් විද්යුත් සංඥා නම්,
ඒ අනුව
මේ අවස්ථා දෙකෙහිදිම වයර්වල
ගමන් කරන්නේ විදුලියනෙ;
එවිට,
ඒ දෙක අතර
වෙනසක් වයර්වලට දැනෙන්නේ
කෙසේද?
සමහර
මාධ්ය ඇනලොග් සංඥාවලට වැඩියෙන්
සුදුසු බව පවසන්නේ කෙසේද?
පිළිතුර
සරලය.
මාධ්ය
හරහා යන සංඥාවේ උපරිම සංඛ්යාතය
තමයි ප්රමුඛ සාධකය.
ඕනෑම
සන්නායකයක්/වයරයක්
හරහා ඕනෑම සංඛ්යාතයක් සහිත
විදුලි සංඥාවකට ගලාගෙන යා
නොහැකිය.
එම සන්නායකය
(මාධ්යය)
සාදා
තිබෙන ස්වභාවය,
කොලිටිය,
මහත ආදී
සාධක අනුව ඒ හරහා යා හැකි සංඥාවේ
උපරිම සංඛ්යාතයක් ඇත.
එම උපරිම
සංඛ්යාතයට වඩා වැඩි සංඛ්යාත
සහිත තරංග ගමන් කරන විට,
අධිසංඛ්යාත
තරංග හායනය (බාල)
වේ.
ඒ කියන්නේ
සංඥා විකෘති වේ.
ඉතිං
සාමාන්ය ඇනලොග් සංඥා යවන
විට, අපට
පහසුවෙන් හැකියි යවන ඇනලොග්
සංඥාවේ (උපරිම)
සංඛ්යාතය
එම මාධ්යයේ උපරිම සංඛ්යාතයට
අඩුවෙන් පවතින ආකාරයට තබන්නට.
තවද,
සංඛ්යාතය
සෙවීමට නම්,
සයිනාකාර
තරංග පැවතිය යුතුයි.
එහෙත්
ඩිජිටල් සංඥාවක් ගත් විට,
එහි උපරිම
සංඛ්යාතය සොයා ගන්නේ කෙසේද
මොකද කොටු තරංගය සයිනාකාර
නොවන නිසා එකවරම සංඛ්යාතය
කිව නොහැකියිනෙ?
එය සෙවීමට
ෆූරියර් න්යාය යෙදිය යුතු
වෙනවා.
අප මීට
පෙර දැනගත්තානෙ ඕනෑම හැඩයක්
සහිත තරංගයක් සයිනාකාර තරංග
සෙට් එකක එකතුවක් ලෙස දැක්විය
හැකියි කියා (එය
තමයි ෆූරියර් න්යායෙන්
ගණිතානුකූලව පෙන්වා දෙන්නේ).
ඉතිං,
කොටු
තරංගයත් අපට හැකියි සයිනාකාර
තරංග සෙට් එකක එකතුවක් ලෙස
දක්වන්නට.
පහත
දැක්වෙන්නේ පිරිසිදු (සමාකාර)
කොටු
තරංගයක් සයිනාකාර තරංග සෙට්
එකක් ලෙස පවතින ආකාරයයි.
ඉහත
සූත්රයේ ඇති රටාව බලන්න.
සූත්රය
හා රූපය අතර තිබෙන සම්බන්දතාවත්
බලන්න.
මූලික
සංඛ්යාතයට (sin2πft)
අමතරව,
සංඛ්යාතයේ
3, 5 ආදී
ලෙස ඔත්තේ ගුණාකාර පමණක්
දිගින් දිගටම පවතින බව පෙනෙනවා
(sin(2πft) ,
sin(6πft) = sin(3(2πft)), sin(10πft) ආදී
ලෙස; 2πf =
ω නිසා
එම පද තවත් පැහැදිලි වන සේ
කෝණික සංඛ්යාතය (ω)
ආශ්රයෙන්
මෙසේ පෙන්වා දිය හැකියි -
sin(ωt), sin(3ωt), sin(5ωt), ...). තවද,
ගුණාකාරය
හෙවත් උපරිතාන (harmonics)
වැඩි වන
විට (එනම්
සංඛ්යාත වැඩි තරංග)
එම කොටස්
ක්රමයෙන් දුබල වෙමින් යනවා
(1/3, 1/5 ආදී
වශයෙන් එක් එක් සයිනාකාර තරංග
ඉදිරියේ ඇති විස්තාර අගයන්
ක්රමයෙන් අඩු වෙනවා).
බලන්න
රතුපාට මූලික තරංගයේ විස්තාරයට
වඩා කොල හා කහ පාට උපරිතාන
තරංග දෙකෙහි විස්තාර අඩුය.
කොල පාට
තෙවැනි උපරිතාන තරංගයේ විස්තාරයට
වඩා කහ පාට පස්වැනි උපරිතානයේ
විස්තාරය අඩුය (ඒ
ආදී වශයෙන් ක්රමයෙන් විස්තාරයන්
හීන වීගෙන යනවා).
එනිසා
න්යායාත්මකව ඔත්තේ ගුණාකාරයන්ගෙන්
දක්වන සයිනාකාර තරංග අනන්ත
ගණනක් දක්වා යා යුතු වුවත්,
ප්රායෝගිකව
ගත් කළ ගුණාකාර 3ක්
හෝ 5ක්
හෝ ඒ ආසන්න ගණනක් පමණක් සලකා
ඉතිරි අධිසංඛ්යාත කොටස්
නොසලකා හැරිය හැකිය.
එහි නිල්
පාටින් දක්වා තිබෙන්නේ මූලික,
පළමු හා
දෙවන උපරිතාන යන තරංග 3
එකතු කළ
විට ලැබෙන හැඩයයි.
බලන්න
එහි කොටු ගතිය හොඳින් මතු වී
තිබෙනවා නේද?
ඊට තවත්
ඉහල උපරිතාන එකතු කරමින් යන
විට නියම පරිපූර්ණ කොටු තරංග
හැඩය තව තවත් මතු වෙනවා (කලු
පාටින් පෙන්වා තිබෙන තත්වයට
පත් වෙනවා).
කොටු
තරංගය සඳහා වූ ඉහත සූත්රයම
පහත ආකාරයටත් දැක්විය හැකියි.
මෙහි
A යනු
කොටු තරංගයේ විස්තාර අගයයි.
අලුත්
සූත්රයේ අමතර පදයක් (½)
ඇත.
එය DC
offset ලෙස
හැඳින්වේ.
එම කොටස
ඉදිරියෙන් ඇති A
පදයෙන්
ගුණ වේ (එනම්
A/2 බවට
පත්වේ).
ඩීසී
ඕෆ්සෙට් එකෙන් සිදු වන්නේ
සමස්ථ තරංග සෙට් එකම තිරස් x
අක්ෂයෙන්
උඩට එසවීමයි.
එහෙත්
මුලින්ම දැක්වූ සූත්රයෙන්
ලැබෙන කොටු තරංග වල ඉහල කොටස්
එක්ස් අක්ෂයෙන් උඩත්,
පහලට ඇති
කොටු එක්ස් අක්ෂයෙන් පහලත්
පවතිනවා.
එහෙත්
මෙම අලුත් සූත්රයෙන් දැක්වෙන
කොටු තරංගයේ ඉහල හා පහල යන
කොටු සියල්ලම පවතින්නේ එක්ස්
අක්ෂයෙන් ඉහලය.
එක්ස්
අක්ෂයෙන් ඉහල හා පහල යන දෙපැත්තේම
තරංග කොටස් පවතින විට ධන හා
ඍණ යන ලකුණු දෙකක් පවතිනවා.
එනිසා
එවැනි තරංග bipolar
ලෙස
හැඳින්වෙනවා.
එහෙත්
යම් තරංගයක් පවතින්නේ එක්ස්
අක්ෂයෙන් සම්පූර්ණයෙන්ම ඉහල
හෝ සම්පූර්ණයෙන්ම පහල නම්,
එවිට එම
තරංගයේ අගය (එනම්
විස්තාර අගය)
එක්කෝ
ධනය (කොටු
ඉහලට වී පවතී නම්);
නැතිනම්
ඍණය (කොටු
පහලට වී පවතී නම්).
එනිසා
එවැනි තරංග unipolar
නමි.
ඒ අනුව,
පළමු
සූත්රය කොටු තරංගය බයිපෝලර්
වන විටත්,
දෙවැනි
සූත්රය යුනිපෝලර් වන විටත්
යෙදිය හැකිය.
යුනිපෝලර්
හා බයිපෝලර් යන භේදය කොටු තරංග
සඳහා පමණක් නොව,
ඕනෑම
විධිමත් හෝ විෂම තරංගයක් සඳහාද
අදාල වේ.
උදාහරණයක්
ලෙස, පහත
දැක්වෙන්නේ සයිනාකාර තරංගයක්
සඳහා එය යෙදෙන ආකාරයයි.
සටහන
DC offset ගැන
යමක් ඉගෙන ගත යුතුය.
ඉහත
උදාහරණයේ එම අගය ½
ලෙස
පැවතිනි.
සෑම විටම
එය යම් සංඛ්යාවක් ලෙස තමයි
පවතින්නේ.
ඒ කියන්නේ
කාලය අනුව එම අගය වෙනස් නොවේ
(ඒ
නිසා එය තරංගාකාරයකින් නොවේ
පවතින්නේ).
ඊට ඩීසී
කියන නම ලැබීමට හේතුව එයයි.
විද්යුත්
සංඥාවක,
සත්ය
වශයෙන්ම එය නිකංම ඩීසී වෝල්ටියතා
අගයක් ලෙස තමයි සලකන්නේ.
මෙලෙස යම්
තරංග සෙට් එකක් අධිස්ථාපනය
(හෙවත්
එකතු) වන
විට, එම
සෙට් එකෙහි ඩීසී සංරචකයක්/පදයක්
තිබෙනවා යනු,
අවසානයේ
ලැබෙන තරංගයට එම ඩීසී අගයත්
එකතු විය යුතුයි කියන එකයි.
එවිට,
එම ඩීසී
අගය ධන අගයක් (+
වෝල්ටියතාවක්)
නම්,
සමස්ථ
සංයුක්ත සංඥාව තිරස් අක්ෂයෙන්
ඉහලට එස වෙනවා.
ඉතිං,
මෙම ධන
ඩීසී අගය ප්රමාණවත් තරම්
විශාල අගයක් නම්,
සංඥාව
මුලුමනින්ම තිරස් අක්ෂයෙන්
ඉහල පිහිටනු ඇත.
එවිට,
එම සංඥාවේ
ඕනෑම තැනක වෝල්ටියතාව මැන්නොත්
එතැන තිබෙන්නේ ධන වෝල්ටියතාවකි.
ඒ කියන්නේ
ඍණ වෝල්ටියතා අගයක් ලැබෙන්නේම
නැත. ධන
හා ඍණ යන ධ්රැව දෙකෙන් තනි
ධ්රැවයක් තිබෙන නිසා තමයි
එබදු සංඥාවකට “ඒකධ්රැව”
(unipolar) කියා
කියන්නේ.
එලෙසම ඩීසී
අගය ඍණ නම් එවිට සංයුක්ත සංඥාව
තිරස් රේඛාවෙන් පහලට වන්නට
පිහිටයි.
ඉතිං,
පෙර සේම
එම ඍණ ඩීසී අගය සමහරවිට සංඥාව
සම්පූර්ණයෙන්ම තිරස් රේඛාවෙන්
පහලට යැවීමට තරම් විශාල වූ
විට, එවිටත්
පෙර සේම යුනිපෝලර් සංඥාවක්
ලැබේ (මොකද
කිසිදු ධන වෝල්ටියතා අගයක්
එම සංඥාවෙ කොතැනවත් දැක ගත
නොහැකි වන නිසා).
ඩීසී සංරචකයක්
නොමැති විට හෝ සංයුක්ත සංඥාව
සම්පූර්ණයෙන්ම තිරස් රේඛාවෙන්
ඉහලට හෝ පහලට විස්ථාපනය කිරීමට
නොහැකි තරම් ලොකු අගයක් නොවන
විට අපට ලැබෙන්නේ ද්විධ්රැව
(bipolar) සංඥාවකි.
ඒ කියන්නේ
දැන් එම සංඥාවේ තැනින් තැන
තිබෙන වෝල්ටියතා අගයන් මැන්නොත්
සමහර කොටස් ධනද සමහර කොටස්
ඍණද ලෙස දක්නට ලැබෙනවා.
ඉතිං,
තිරස්
රේඛාවෙන් උඩට හෝ යටට සංයුක්ත
සංඥාව විස්ථාපනය (offset)
කිරීමේ
හැකියාවක් මෙම ඩීසී පදයට ඇත.
එනිසයි
එය DC offset
කියා නම්
කෙරෙන්නේ.
ඇත්තෙන්ම,
යම් සංයුක්ත
සංඥාවකින් ඩීසී සංරචකය ඉවත්
කළත් සංඥාවේ හැඩය එලෙසම පවතිනවා.
සිදුවන
එකම වෙනස සංඥාව ඉහලට හෝ පහලට
තරමක් විස්ථාපනය වීම පමණි.
මේ
අනුව දැන් මෙතැන් සිට ඔබ යමක්
හොඳින් තේරුම්ගත යුතුය.
කොටු
හැඩැති ඩිජිටල් තරංගයක් යනු
සයිනාකාර තරංග සෙට් එකක් බවයි;
තවද එහි
මූලික සංඛ්යාතය හා එහි ඔත්තේ
ගුණාකාර කිහිපයකින් යුතු
සයිනාකාර තරංග ලෙස ඒවා පවතින
බවයි.
ප්රායෝගික/සත්ය
ඩිජිටල් සංඥා ඉහත ආකාරයට
පිරිසිදු කොටු තරංග නොවේ
(මාරුවෙන්
මාරුවට එක කොටුවක් උඩත් ඊළඟ
කොටුව පහලට සිටින සේ තිබෙන
තරංග නොවේ).
එහෙත්
මූලික සිද්ධාන්තය එලෙසම තේරුම්
ගන්න.
යම්
ඩිජිටල් තරංගයක් (කොටු
තරංගයක්)
ගත් විට,
එහි එක්
කොටුවක් එලෙස පවතින කාල පරාසය
(period) වැදගත්
පරාමිතියකි.
එය bit
period, bit interval, bit duration යන
වචනවලින් හැඳින්විය හැකිය
(කෙටියෙන්
tb ලෙස
සංඛේතවත් කෙරේ).
එවිට,
1/tb යනු
දළ වශයෙන් එම බිට් ගමන් කරන
දත්ත සම්ප්රේෂණ වේගය (bit
rate – bits per second (bps)) වේ.
ඉතිං,
යම් ඩිජිටල්
සංඥාවක් ෆූරියර් විශ්ලේෂණයෙන්
ලැබෙන ෆූරියර් සංරචක අතර පවතින
ප්රධානතම තරංගය වන මූලික
තරංගයේ (fundamental)
සංඛ්යාතය
දල වශයෙන් 1/tb
මෙන්
දෙගුණයකි.
ඉතිං
ඩිජිටල් කොටු තරංගයේ කොටු
ස්වභාවය සෑහෙන්න දුරකට එලෙසම
පවත්වා ගෙන යෑමට නම්,
මූලික
තරංගයත් එහි පළමු ඔත්තේ උපරිතාන
2ක්
අඩුම වශයෙන් මාධ්ය හරහා
යැවීමට සිදු වෙනවා.
සාමාන්යයෙන්
ඩිජිටල් සංඥාවල දත්ත වේගය
වැඩිය (ඇනලොග්
සංඥාවක් ඩිජිටල් කරපු විට,
අති විශාල
බිට් තොගයක් ලැබෙන නිසා).
ඊට අමතරව
ඉහත පෙන්වා දුන් කාරණය අනුව,
ඩිජිටල්
සංඥාවේ උපරිම සංඛ්යාතය වන්නේ
මූලික සංඛ්යාතය මෙන් තුන්
ගුණයක් හෝ පස් ගුණයක් හෝ වන
සංඛ්යාතයකි.
ඒ කියන්නේ
අවසන් ප්රතිපලය වන්නේ ඩිජිටල්
සංඥාවල අධිසංඛ්යාත තරංග
පවතින බවයි.
ඉතිං,
මාධ්යයට
හැකි විය යුතුයි මෙම අධිසංඛ්යාත
තරංග හායනයකින් තොරව යවන්නට.
මේ සඳහා
විශේෂ ආකාරවලට සෑදූ තත්වයෙන්
උසස් වයර් අවශ්ය කෙරේ.
උදාහරණයක්
ගතහොත්,
රැහැන්
දුරකතන සඳහා ඇද තිබෙන (පැරණි)
වයර්
තත්වයෙන් උසස් අධිසංඛ්යාත
යෑමට උචිත නැත.
ඊට හේතුව
ටෙලිෆෝන්වලදී කටහඬෙහි ඉහල
සංඛ්යාත කොටස් කපා හරින අතර,
අනෙකාට
තේරුම් ගැනීමට හැකි පමණ
කොලිටියක් පමණක් තබා ගන්නවා
(ඒකනෙ
ටෙලිෆෝන් එකකින් කතා කරන විට
කටහඬ තරමක් අඩු කොලිටියකින්
ඇසෙන්නේ).
ඒ කියන්නේ
අධිසංඛ්යාත තරංග එම වයර්වල
යවන්නේ නැත.
එනිසා
මිලෙන් අඩු “තත්වයෙන් බාල”
වයර් ඒ සඳහා භාවිතා කළ හැකියි.
ඉතිං,
මෙවැනි
(පැරණි)
ටෙලිෆෝන්
කම්බියක් හරහා ඩිජිටල් සංඥා
යැවීමට සිදු වුවොත්,
එම දත්ත
සම්ප්රේෂණ වේගය ඉතා මන්දගාමී
වනු ඇත මොකද සංඛ්යාතය අඩුවෙන්
පැවතීමට නම්,
තත්පරයට
යැවිය යුතු බිට් ගණන හෙවත්
දත්ත සම්ප්රේෂණ වේගය අඩු
විය යුතු නිසාය.
කාලෙකට
උඩදී බොහෝ දෙනා ඉන්ටර්නෙට්
එකට සම්බන්ද වූ ප්රචලිත (හා
ඒකාලයේ ලාභම)
ක්රමය
වූයේ මෙවැනි රැහැන් දුරකතන
සම්බන්දතාවක් භාවිතා කිරීමයි
(ADSL, 3G/HSPA
වැනි
ක්රම එකල නොතිබුණි).
මෙම ක්රමය
dial-up network
(DUN) connection ලෙස
හැඳින්වේ.
අදටත්
එම ක්රමයෙන් අන්තර්ජාලයට
සම්බන්ද විය හැකියි.
මෙහිදී
සාමාන්ය ටෙලිෆෝන් වයර් යනු
ඇනලොග් සංඥා සඳහා පමණක් සැකසූ
මාධ්යයක් වන අතර,
පරිගණකය
යනු ඩිජිටල් සංඥා සමග වැඩ කරන
උපකරණයකි.
ඉතිං,
ඔබේ
පරිගණකයේ සිට එන ඩිජිටල් සංඥා
ඇනලොග් ටෙලිෆෝන් වයර් එකට
සුදුසු ඇනලොග් සංඥා බවට පත්
කළ යුතුය (මොඩ්යුලේෂන්).
තවද,
අන්තර්ජාලයේ
සිට ඔබේ පරිගනකය වෙත ටෙලිෆෝන්
වයර් එක දිගේ ඇනලොග් සංඥා
ඩිජිටල් සංඥා බවට පත් කළ යුතුය
(ඩිමොඩ්යුලේෂන්).
මෙම
මොඩ්යුලේෂන් හා ඩිමොඩ්යුලේෂන්
ක්රියාවලින සිදු කරන්නේ
අතරමැදි මෝඩෙම් (modem)
නම් විශේෂිත
උපාංගයකිනි.
ඊට එම නම
ලැබී තිබෙන්නේ Modulator
+ Demodulator යන
වචන දෙක කෙටි වීමෙනි.
එහෙත්
ටෙලිෆෝන් වයර් පෙර පැහැදිලි
කළ ලෙස අධිසංඛ්යාත සඳහා
සුදුසු නැති නිසා,
දත්ත
සම්ප්රේෂන වේගය ඉතා මන්දගාමී
වේ (උපරිම
වේගය තත්පරයට කිලෝබිට් 56කි).
අද පවතින
වේගවත් (තත්පරයට
කිලෝබිටි 8000
වැනි)
බ්රෝඩ්බෑන්ඩ්
ඉන්ටර්නෙට් සම්බන්දතා වේගයන්
හා සසඳන විට,
එම වේගය
ඉබි ගමනක් බදුය.
එහෙත්
ඩයල්අප් ක්රමයේ තිබූ වාසිය
වන්නේ අන්තර්ජාල සේවා සපයන
ආයතනවලට තමන් සතුව දැනටමත්
තිබූ සාමාන්ය දුරකතන යටිතල
පහසුකමට ඉතාම අඩු වියදමක්
දරා අන්තර්ජාල සම්බන්දතා
පහසුකම සපයා දීමට හැකි වීමයි.
දැනටමත්
තිබෙන ටෙලිෆෝන් වයර් එලෙසම
තබා ගෙන,
තම
එක්ස්චේන්ජ් එකේ මොඩෙම් සවි
කිරීමට පමණයි ඔවුන්ට සිදු
වන්නේ.
එහිදී
අපේ පරිගනකයේ සිට යන ඩිජිටල්
සංඥා අපේ පරිගනකයේ සවි කර
තිබෙන මොඩෙම් එකට ගොස් ඇනලොග්
බවට පත්ව,
එම ඇනලොග්
සංඥා ටෙලිෆෝන් වයර් දිගේ ගොස්,
ටෙලිකොම්
සේවා සපයන්නාගේ එක්ස්චේන්ජ්
එකේ ඇති මොඩෙම් එකට ඇතුලු වේ.
ඉන්පසු
එම මොඩෙම් එකෙන් ඇනලොග් සංඥා
නැවත ඩිජිටල් කර ටෙලිකොම්
සේවා සපයන්නාගේ අභ්යන්තර
ජාලය හරහා අන්තර්ජාලයට සම්බන්ද
වේ. ආපස්සට
අන්තර්ජාලයේ සිට දත්ත එන
විදියත් ඒ අනුව තේරුම් ගන්න.
අන්තර්ජාලයට
සම්බන්ද වීමට අමතරව මෙම
ක්රමයෙන්ම හැකියි ඈත තිබෙන
පරිගණක දෙකක් හෝ පරිගනක ජාල
(network) දෙකක්
එකතු කරන්නත්.
පහත
දැක්වෙන්නේ ඈත තිබෙන පරිගනක
දෙකක් ටෙලිෆෝන් ජාලයක් හරහා
ඩයල්අප් ක්රමයට එකිනෙකට
සම්බන්ද වන ආකාරයයි. උදාහරණයක්
ලෙස, කලකට
ඉහතදී රජයේ මුද්රණාල
දෙපාර්තමේන්තුවේ අභ්යන්තර
පරිගනක ජාලයට මහජනයාට ප්රවේශ
වීමට මෙම පහසුකම සපයා තිබුණා
(ගැසට්පත්රය
බැලීමට). තාක්ෂණිකව
මෙලෙස තවත් පරිගනකයට සමබන්ද
වී එම පරිගනකයේ ඇති යම් සේවාවක්
ලබා ගැනීම Bulletin
Board System (BBS) ලෙස
හැඳින්වේ.
අන්තර්ජාලය
ප්රචලිත නොවූ එකල අද අපි
අන්තර්ජාලයට සම්බන්දව ෆයිල්
එහා මෙහා යැවීම,
යම් යම්
තොරතුරු හුවමාරු කිරීම,
ගේම්
ගැසීම,
චැට්
කිරීම ආදී කටයුතු සිදු කළේ
මෙවැනි BBS
හරහාය.
එහෙත්
අන්තර්ජාලය ප්රචලිත වීමත්
සමගම මෙම සේවා ක්රමයෙන්
අභාවයට ගියේය.
ඉහත
විස්තර කළේ ප්රායෝගිකව
ඩිජිටල් සම්ප්රේෂණය සිදු
කරපු එක් අවස්ථාවකි.
මේ වන
විට, සියලුම
ජංගම දුරකතන සේවා ඩිජිටල්
සම්ප්රේෂණ ක්රම තමයි භාවිතා
කරන්නේ.
බොහෝ
රටවල, ටීවී
හා රේඩියෝ සේවාද දැන් ඩිජිටල්
ආකාරයෙන් සිදු වේ (ලංකාව
නුදුරේදි එම තත්වයට පත් වෙන්නට
නියමිතය).
වයිෆයි,
බ්ලූටූත්
ආදියත් එසේමය.
ඉතිං
මොනවාද මේ ඩිජිටල් මූර්ජන
ක්රම?
එකින්
එක දැන් සලකා බලමු.

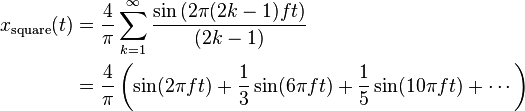








Comments
Post a Comment
Thanks for the comment made on blog.tekcroach.top