සන්නිවේදනය හා ආධුනික ගුවන් විදුලිය (Amateur radio) 24

කලා මූර්ජනය

කලා මූර්ජනය (phase modulation – PM) යනු මූර්ජන හෙවත් බුද්ධි තරංගයේ විස්තාර අගයට අනුරූපව වාහක තරංගයේ කලාව විචලනය කිරීමයි. එහිදී සංඛ්‍යාත මූර්ජනයේදී මෙන්ම දෙයාකාරයකින් එය සිදු කළ හැකියි.

1. මූර්ජන තරංගයේ විස්තාර අගය වැඩි වන විට කලා වෙනස “ඉදිරිගාමී” (leading) වන ලෙස වාහකයේ කලා අගය විචලනය කිරීමයි. එවිට, මූර්ජන තරංගයේ විස්තාර අගය (උඩ ධන පැත්තට) වැඩි වේගෙන යන විට, වාහක තරංගය වැඩි වැඩියෙන් ඉදිරිගාමී වීම නිසා තරංග ආයාමය එන්න එන්න කෙටි වේගෙන යයි. එනම් වාහක තරංගය සංකෝචනය වෙනවා සේ පෙනේ. එයම අපට දැකිය හැකියි වාහක තරංගයේ සංඛ්‍යාතය වැඩි වනවා කියා. මෙම ක්‍රමයේදීම, ඒ අනුව මූර්ජන තරංගයේ විස්තාර අගය ක්‍රමයෙන් අඩුවන විට (හෙවත් යට ඍණ පැත්තට වැඩිවන විට), තරංගය දිගු (ප්‍රසාරණය) වෙනවා සේ පෙනේ. එනම්, දැන් වාහක සංඛ්‍යාතය අඩු වේ.

2. මූර්ජන තරංගයේ විස්තාර අගය වැඩි වන විට කලා වෙනස “පසුගාමී” (lagging) වන ලෙස වාහකයේ කලා අගය විචලනය කිරීමයි. මෙවිට වාහකයේ වෙනස් වීම ඉහත පළමු අවස්ථාවේ සඳහන් විග්‍රහයට ප්‍රතිවිරුද්ධ ආකාරයට සිදු වේ. ඒ අනුව, මූර්ජන තරංගයේ විස්තාර අගය වැඩි වේගෙන යන විට, වාහක තරංගය දිගු වේ (සංඛ්‍යාතය අඩු වේ). මූර්ජන තරංගයේ විස්තාර අගය අඩු වේගෙන යන විට, වාහක තරංගය සංකෝචනය වේ (සංඛ්‍යාතය වැඩි වේ).

මෙම පාඩමේදී මෙතැන් සිට අප යොදා ගන්නේ ඉහත පළමු ක්‍රමයට සිදුකරන කලා මූර්ජනයයි.

තවද, ඉහත විස්තර අනුව පැහැදිලිවම පෙනෙනෙවා වාහකයේ කලාව වෙනස් වීමත් අපට භාහිරින් පෙනෙන්නේ වාහකයේ සංඛ්‍යාතය වෙනස් වීමක් ලෙසයි. එනිසා බැලූබැල්මට කලා මූර්ජනයට ලක්ව ඇති සංඥාවක් හා සංඛ්‍යාත මූර්ජනයට ලක්ව ඇති සංඥාවක් එකවර වෙන් කොට හඳුනාගැනීමට නොහැකි විය හැකිය. එසේ වුවත්, මෙම දෙකෙහි සියුම් වෙනස්කමක් ඇත. දැන් ඒ ගැන විමසා බලමු.

පහත රූපය බලන්න. එහි එකම මූර්ජන තරංගයක් හා එකම වාහක තරංගයක් ගෙන, එකක් සංඛ්‍යාත මූර්ජනය අනුවද, දෙවැන්න දැන් කතා කරමින් සිටින කලා මූර්ජනය අනුවද වෙන වෙනම මූර්ජනය කළ විට ලැබෙන අවසාන තරංග හැඩ දක්වා ඇත (වඩා පැහැදිලිව පෙන්වීම සඳහා වාහක තරංගය සාමාන්‍ය සයිනාකාර හැඩයෙන් නැතිව ත්‍රිකෝණකාර තරංග හැඩයෙන් දක්වා ඇත). බලන්න, මූර්ජිත තරංග දෙකම මූර්ජන තරංගයට අනුරූපව තම සංඛ්‍යාතයන් වෙනස් කරගෙන තිබෙනවා. එසේ වුවත්, ඒ මූර්ජිත තරංග දෙක සර්වසම නැහැ නේද? මූර්ජිත තරංග දෙකෙහි තරංගය හැකිලීම හා ප්‍රසාරණය වීම (එනම් සංඛ්‍යාතය අඩු හා වැඩි වීම) සිදු වන්නේ වෙනස් වෙනස් තැන්වලයි (නිල් පාට රවුම තුල බලන්න).

 

ඉහත පෙන්වූ වෙනසට හේතුව තමයි අපි දැන් සොයන්නට යන්නේ. එම වෙනස හැරෙන්නට FM හා PM දෙකම සමාන වේ. ඇත්තටම මෙම වෙනස ඇති වන හේතුව සොයා, එම වෙනස ඇති නොවීමට යම් උපක්‍රමයක් යෙදිය හැකි නම්, කලා මූර්ජනය සංඛ්‍යාත මූර්ජනයක් බවට ඉබේම පත් වේ. එය කළ හැකිය. ඒ අනුව, සුදුසු උපක්‍රමයකින් එය සිදු කරමින් සාදා ගන්නා සංඛ්‍යාත මූර්ජනය Indirect FM ලෙස හැඳින්වේ (මීට පෙර උගත් සුපුරුදු සංඛ්‍යාත මූර්ජන ක්‍රමය Direct FM ලෙස හැඳින්වේ). ඒ ගැන මොහොතකින් බලමු.

සංඛ්‍යාත මූර්ජනයේදී බුද්ධි සංඥාවේ විස්තාර අගය (වෝල්ටියතාව) අනුව එහි සංඛ්‍යාතය වෙනස් කරගන්නවානෙ. ඉතිං කිසිදු බුද්ධි සංඛ්‍යාවක් නැති (වෝල්ටියතාව ශූන්‍ය) විට එෆ්එම් සංඥාව වාහක සංඥාව බවට පත් වෙනවානෙ (එනම් මූර්ජිත සංඥාව වාහක සංඥාවේ සංඛ්‍යාතය ගන්නවා). එහෙත් බුද්ධි සංඥාවේ වෝල්ටියතාව අඩු හෝ වැඩි වන විට, ඊට අනුරූපව එෆ්එම් සංඥාවේ සංඛ්‍යාතයත් අඩු හෝ වැඩි විය. දැන් සිතන්න, බුද්ධි සංඥාවේ වෝල්ටියතාව ක්‍රමයෙන් වැඩි වී, යම් අවස්ථාවකට පසුව යම් කාලයක් පුරාවටම එම වෝල්ටියතාව නොවෙනස්ව එම අගයේම නියතව පැවතියේ යැයි කියා. එවිට එෆ්එම් සංඥාවේ සංඛ්‍යාතයද බුද්ධි සංඥාවේ වෝල්ටියතාව ක්‍රමයෙන් වැඩිවේගෙන යන විට ක්‍රමයෙන් වැඩි වීගෙන ගොස්, බුද්ධි සංඥාවේ වෝල්ටියතාව නියත වන විට, එෆ්එම් සංඥාවේ සංඛ්‍යාතයද තවදුරටත් වැඩි හෝ අඩු නොවී ඒ තිබූ අගය දිගටම පවත්වාගෙන යනවා (නියත වෙනවා).

ඉහත ඡේදයේ සිදු වූ දේ දැන් කලා මූර්ජනයේදී හැසිරෙන්නේ කෙසේදැයි බලමු. කිසිදු බුද්ධි සංඥාවක් නැති (වෝල්ටියතාව ශූන්‍ය) විට පීඑම් සංඥාව (හෙවත් කලා මූර්ජිත සංඥාව – Phase Modulated signal) වාහක සංඥාව බවට පත් වේ. එහෙත් බුද්ධි සංඥාවේ වෝල්ටියතාව අඩු හෝ වැඩි වන විට, ඊට අනුරූපව පීඑම් සංඥාවේ කලාව (එවිට, වක්‍රාකාරයෙන් එහි සංඛ්‍යාතය) දැන් අඩු හෝ වැඩි වෙනවානෙ. එහෙත් මෙතැන තමයි වෙනස මතු වන්නේ. කලා මූර්ජනයේදී අවසාන මූර්ජිත තරංගයේ විචලනය සිදු වන්නේ සතතයෙන් හෙවත් නොනවත්වාම (continuously) මූර්ජන සංඛ්‍යාතයේ වෝල්ටියතාව විචලනය වේ නම් පමණි. ඒ අනුව, බුද්ධි සංඥාවේ වෝල්ටියතාව ක්‍රමයෙන් වැඩි වෙමින් යන විට, පීඑම් සංඥාවේ සංඛ්‍යාතයද ක්‍රමයෙන් වැඩි වේ (අපි මෙම පාඩමේදී යොදා ගන්නේ ඉහතකදී පැවසූ ක්‍රම දෙකෙන් පළමු ක්‍රමය බැවින්, මූර්ජන තරංගයේ වෝල්ටියතාව වැඩි වන විට මූර්ජිත තරංගයේ සංඛ්‍යාතයද වැඩි වේ). ඉන්පසු, මූර්ජන තරංගයේ විස්තාර අගය යම් වෝල්ටියතා අගයකට පත් වූ පසුව එම අගය දිගටම නියතව පවත්වාගෙන යන කාලය තුලදී, පීඑම් සංඥාව පවතින්නේ කිසිදු බුද්ධි සංඥාවක් නැති විට පවතින ආකාරයටමයි. එනම් වාහක තරංගයේ සංඛ්‍යාතය ගනී. කිසිවිටක මෙම නියත අවස්ථාවේදී සංඛ්‍යාත මූර්ජනයේදී මෙන් ඉහල සංඛ්‍යාතයකින් යුතුව නියත සංඛ්‍යාත අගයක් පවත්වාගෙන යන්නේ නැත.

මේ නිසා කලා මූර්ජනයට “ගතික” (dynamic) බවක් තිබේ යැයි කිව හැකිය (ගතික යන්නෙහි සරල තේරුම “විසේකාර” යන්නයි; එනම් නිතරම දැඟලිල්ලක් තිබිය යුතුය). ඒ කියන්නේ, කලා මූර්ජනයේදී කරුණු දෙකක් වැදගත් වේ.

1. මූර්ජන තරංගයේ වෝල්ටියතා මට්ටම හෙවත් විස්තාරය

2. එම වෝල්ටියතා මට්ටම (විස්තාරය) සතතයෙන් විචලනය වෙමින් පැවතීම (විචලන සීඝ්‍රතාව – rate of variation/change).

පහත දැක්වෙන්නේ ඉහත වෙන් වෙන්ව දැක්වූ රූප දෙක එකට ගෙන සංඛ්‍යාත හා කලා මූර්ජන දෙක වෙනස් වන ආකාරය පහසුවෙන් සංසන්දනය කළ හැකි රූපයකි.

t₀ කාලය තුල මූර්ජන තරංගය ශූන්‍ය බැවින්, එෆ්එම් හා පීඑම් සංඥා දෙකම පවතින්නේ වාහකයේ සංඛ්‍යාතයේමය (එනම් වාහක තරංගයේ සංඛ්‍යාතය පවත්වාගෙන යයි).

t₁ කාලය තුල මූර්ජන තරංගය ශූන්‍ය අගයේ සිට (ධනව) වැඩි වන නිසා, එෆ්එම් හා පීඑම් සංඥා දෙකම තමන්ගේ සංඛ්‍යාතයන් ක්‍රමයෙන් වැඩි කර ගන්නවා. තවද, පීඑම්වල සංඛ්‍යාතය වැඩි කර ගැනීම තරංගය තිරස් x අක්ෂය කපන අවස්ථාවේදී (zero crossing) ඉතා වැඩිය (ඊට හේතුව මොහොතකින් බලමු). ඒ කියන්නේ මූර්ජන තරංගයේ වෝල්ටියතාව වැඩිවෙමින් තිරස් රේඛාව කපන විට පීඑම් සංඥාවේ උපරිම සංඛ්‍යාතය ලැබෙනවා.

t₂ කාලය තුල මූර්ජන තරංගය වැඩි (ධන) වෝල්ටියතා අගයක් නියතව පවත්වාගෙන යන නිසා, එෆ්එම් සංඥාව තමන් වැඩිකර ගත් සංඛ්‍යාතය එලෙසම නියතව පවත්වාගෙන යයි. එහෙත් පීඑම් සංඥාව එසේ නැත. පීඑම් සංඥාවේ සංඛ්‍යාතය වාහක තරංගයේ සංඛ්‍යාතයට සමාන වේ.

t₃ කාලය තුල මූර්ජන තරංගය ඍණ පැත්තට වැඩි වන නිසා, මූර්ජන තරංගයේ වෝල්ටියතාව අඩු වන බැවින්, එෆ්එම් හා පීඑම් සංඥා දෙකත් තමන්ගේ සංඛ්‍යාතයන් ක්‍රමයෙන් අඩු කර ගන්නවා. තවද, පීඑම් හිදී තරංගය තිරස් අක්ෂය කපන අවස්ථාවේදී ලොකුම සංඛ්‍යාත අඩු වීම සිදු කර ගන්නවා.

t₄ කාලය තුල, මූර්ජන තරංගයේ අගය නැවත නියත වේ. එවිට, එෆ්එම් සංඥාව තමන් එම අවස්ථාවේ තිබී සංඛ්‍යාතය දිගටම එලෙසම නොවෙනස්ව පවත්වාගෙන යනවා. එහෙත්, සුපුරුදු ලෙසම, පීඑම් සංඥාව පත්වන්නේ වාහක තරංගයේ සංඛ්‍යාතයටයි.

බලන්න t₂, t₄ යන කාලාන්තර දෙක තුලදී පීඑම් සංඥාව නිකංම වාහක තරංගයේ සංඛ්‍යාතය බවට පත්ව ඇත. තවද, t₁, t₃, t₅ යන කාලාන්තරවලදී පීඑම් තරංගයේ සංඛ්‍යාතය උපරිමව වෙනස් වේ. එනම් මූර්ජන සංඥාවේ වෝල්ටියතාව සීඝ්‍රයෙන් වෙනස් කරන විටයි පීඑම් සංඥාවේ සංඛ්‍යාතය සීඝ්‍රයෙන් වෙනස් කර ගන්නේ. මූර්ජන සංඥාවේ වෝල්ටියතාව වෙනස් නොකර නියතව පවත්වා ගන්නා විට, පීඑම් සංඥාව තම සංඛ්‍යාතය වාහක තරංගයේ සංඛ්‍යාතයෙන් පවත්වාගෙන යනවා. පීඑම් මූර්ජනය ආශා කරන්නේ මූර්ජන තරංගයේ දැඟලිල්ලටයි. ඒ කියන්නේ බුද්ධි සංඥාව තිරස් x අක්ෂය කපන සෑම අවස්ථාවකදීම පීඑම් සංඥාවේ වැඩිම සංඛ්‍යාත වෙනස සටහන් වේ (මූර්ජන තරංගය ධන සිට ඍණට හෝ ඍණ සිට ධනට ගමන් කරන විට).

ඒඑම් හා එෆ්එම් මූර්ජනවලදී මෙන්ම පීඑම් මූර්ජනයේදීද සුපුරුදු කාර්යන් දෙක (එනම්, අවසංඛ්‍යාත බුද්ධි සංඥාව අධිසංඛ්‍යාත වාහක සංඥාවට කාවැද්දීම හා අපට අවශ්‍ය සංඛ්‍යාත කලාපයක බුද්ධි සංඥාව ස්ථානගත කිරීම) එලෙසම සිදු වේ. බුද්ධි සංඥාවේ බුද්ධිය (තොරතුරු) වාහක සංඥාවේ කලා වෙනස තුල ඍජුව (එවිට වාහකයේ සංඛ්‍යාතය වක්‍රව වෙනස් වීමෙන්) කැවැද්දේ. තවද, සුදුසු සංඛ්‍යාතයක් සහිත වාහකයක් යොදා ගැනීමෙන් අපට අවශ්‍ය සංඛ්‍යාත කලාපයකට බුද්ධි සංඛ්‍යාතය ඔසවා තැබේ.

බුද්ධි සංඥාව, m(t) = a_mcos2πf_mt නම්, හා වාහක තරංගය a_ccos2πf_ct නම්, පහත ආකාරයට ගණිතානුකූලව කලා මූර්ජිත සංඥාව දැක්විය හැකිය. මෙහි k_p යන නියත පදයෙන් අදහස් කෙරෙන්නේ බුද්ධි තරංගයේ විස්තාරයට (වෝල්ටියතාවට) කොතරම් අනුපාතයකින් වාහකයේ කලාව වෙනස් වන්නේද කියාය (radians per volt – radV^-1). එය phase sensitivity කියා හැඳින්වෙන අතර, පරිපථය නිර්මාණය කරන කෙනා විසින් එම නියත අගය තීරණය කරනවා.

s(t) = a_ccos(2πf_ct + k_pm(t))

= a_ccos(2πf_ct + k_p(a_mcos2πf_mt)) = a_ccos(2πf_ct + u_pcos2πf_mt)

සංඛ්‍යාත මූර්ජනයේදී මෙන්ම, කලා මූර්ජනයේදීත් ඉහත සමීකරණයට විසඳුම ලැබෙන්නේ බෙසල් ශ්‍රිතය ආශ්‍රයෙනි. එෆ්එම් හා පීඑම් දෙකටම එකම ආකාරයෙන් එය බලපානවා. එහිදී බෙසල් ශ්‍රිතයේ ප්‍රස්ථාරයද එලෙසම මෙහි භාවිතා කළ හැකිය. තවද, එෆ්එම්වල හමුවූ බෙසල් පද ප්‍රසාරණයම පහත සංක්ෂිප්ත ආකාරයෙන්ද දැක්විය හැකිය.

එෆ්එම් මූර්ජනයේ හමු වූ සියලු විස්තර එලෙසම පීඑම් මූර්ජනයට බලපාන නමුත්, එක් එක් J සංගුණක පදවල අගයන් ගණනය කරන සූත්‍රයේදී m_f යන තැන u_p ආදේශ කරන්න. එච්චරයි (නැවත එෆ්එම් මූර්ජන පාඩම කියවා බලන්න).

තවද, පීඑම් මූර්ජනයේදී අවශ්‍ය කරන බෑන්ඩ්විත් එක එෆ්එම් ක්‍රමයේදී මෙන්ම ගණනය කළ හැකියි. කාර්සන්ගේ නියමයද එලෙසම යෙදිය හැකිය.

මේ අනුව පැහැදිලි වෙනවා, සංඛ්‍යාත හා කලා මූර්ජන ක්‍රම දෙකම ඉතාම සමීප බව. එසේ වුවත් පෙර අවස්ථාවකත් සඳහන් කළ ලෙසම, කලා මූර්ජනයේදී කලාව වෙනස් වීම (එවිට, සංඛ්‍යාත අපගමනය) මූර්ජන තරංගයේ වෝල්ටියතා අගයට අමතරව, මූර්ජන තරංගයේ සංඛ්‍යාතය අනුවත් විචලනය වේ (පීඑම් හි ගතික බව). එෆ්එම්වලදී මූර්ජන තරංග සංඛ්‍යාතය අවසාන එෆ්එම් තරංගයට බලපෑවේ නැත. පහත ප්‍රස්ථාර බලන්න.

අවසාන වශයෙන් පීඑම් මූර්ජනය එෆ්එම් මූර්ජනයට අනකූල වන පරිදි සෑදිය හැකි (indirect FM) ආකාරය බලමු. කළ යුත්තේ මූර්ජන තරංගයේ සංඛ්‍යාතයට සිදුවන විචලනය උදාසීන කර දැමීමයි. ඒ සඳහා අපට කදිම උපක්‍රමයක් යෙදිය හැකිය. එනම්, බුද්ධි තරංගයේ සංඛ්‍යාත කලාපය පටන් ගන්නා සංඛ්‍යාතයේ සිට අවසාන වන සංඛ්‍යාතය දක්වා කොටස සංඛ්‍යාතය වැඩි වන දිශාවට ක්‍රමයෙන් බුද්ධි සංඥාව හායනය (attenuation) කිරීමයි.

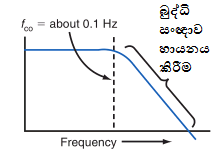
ඉහත හායනය ඉතාම පහසුවෙන් කළ හැකියි Low Pass Filter (LPF) එකක් හරහා බුද්ධි සංඥාව ගමන් කරවීමෙන්. මෙම අවස්ථාවේදී මෙම ෆිල්ටරය Predistorter, 1/f filter හෝ frequency correcting network යන නම්වලින් හැඳින්වෙනවා. මෙම ෆිල්ටරය හරහා ගිය බුද්ධි සංඥාව දැන් කෘත්‍රිමව හායනයකට ලක් කර ඇත (සංඛ්‍යාතය ක්‍රමයෙන් වැඩි වන විට හායනයද ක්‍රමයෙන් වැඩි වේ). ඉන්පසු සපුරුදු පීඑම් මූර්ජනයට ලක් කළ විට, සංඛ්‍යාතය වැඩිවීම නිසා සිදුවන වැඩිපුර සංඛ්‍යාත අපගමනය උදාසීන වේ (මොකද සංඛ්‍යාතය වැඩි කොටස් තුල බුද්ධි සංඥාවේ වෝල්ටියතාව අඩු වන අතර එවිට එම වෝල්ටියතාව නිසා සිදුවන අපගමනයද අඩු වේ).