ඉලෙක්ට්‍රෝනික්ස් IV (Electronics) - 18

කර්චොෆ්ගේ මූලධර්ම

මෙතෙක් සිදු කළ පරිපථ විශ්ලේෂන තුල හා ඉදිරියේදිත් මා නිතරම යොදා ගත් පරිපථ විශ්ලේෂන නියම දෙකක් ඇත. ඒවා කර්චොෆ්ගේ නියම වේ. කර්චොෆ් නමැත්තා විසින් ප්‍රචලිත කර වූ බැවින් ඔහුගේ නමින්ම මේ නියම නම් කර ඇත. මේවා තේරුම් ගැනීම මෙන්ම යොදා ගැනීමද සරලය. කර්චොෆ්ගේ නියම 2ක් පවතිනවා.

1. කර්චොෆ්ගේ වෝල්ටියතා නියමය (Kirchoff’s Voltage Law – KVL)

2. කර්චොෆ්ගේ ධාරා නියමය (Kirchoff’s Current Law – KCL)

වෝල්ටියතා නියමය කර්චොෆ්ගේ පුඩු නියමය (Kirchoff’s Loop Law) ලෙසද හැඳින්වෙන අතර, ඉන් කියන්නේ විදුලිය ගමන් කරන එක් සංවෘත පථයක, එක් තෝරාගත් දිශාවක් ඔස්සේ පවතින වෝල්ටියතාවන් සියල්ලෙහිම එකතුව ශූන්‍ය වන බවයි. ΣV = 0 ලෙස ගණිතානුකූලව එය ඉදිරිපත් කළ හැකිය.

ඉහත රූපය බලන්න. එහි V_S නම් වෝල්ටියතා සැපයුමක්/ප්‍රභවයක්/බැටරියක් සහිතව රෙසිස්ටර් දෙකක් ඇත. කර්චොෆ්ගේ වෝල්ටියතා නියමය යෙදීමේදී කොන්දේසිය වන්නේ සංවෘත පථයක් හෙවත් පරිපථයක් පැවතීමයි. එය වලල්ලක්/පුඩුවක් ලෙස පෙනෙන නිසා තමයි පුඩු නියමය යන නමත් යෙදෙන්නේ. දැන් පලමුවෙන්ම කළ යුත්තේ, එම පරිපථයේ වාමාවර්ත හා දක්ෂිණාවර්ත යන කරකැවීමේ දිශා දෙකෙන් එකක් තෝරා ගැනීමයි. ඔබට කැමති දිශාවක් තෝරා ගත හැකිය. ඉහත ආකාරයේ එක් විභව සැපයුමක් සහිත අවස්ථාවකදී බොහෝ අයට එකවර සිතෙන්නේ එම සැපයුමේ ධන අග්‍රයෙන් පටන් ගන්නා ලෙස එම දිශාව තෝරා ගැනීමයි. එනම් පරිපථය හරහා සත්‍ය ලෙසම ධාරාව ගමන් කරන දිශාවම තෝරා ගැනේ. ඉහත රූපයේද කර තිබෙන්නේ එයයි; එහෙත් වෝල්ටියතා සැපයුම් කිහිපයක් තිබෙන විට එකවරම ධාරාව පරිපථය හරහා සත්‍ය ලෙසම ගලා යන දිශාව කිව නොහැකි වන්නටත් පුලුවන්.

සටහන

පහත වම් රූපයේ පරිපථයේ ධාරාව ගලා යන්නේ කුමන දිශාව ඔස්සේද? එය ටිකක් විමසා බලා දැනගත යුතුය.

එක් එක් විභව සැපයුම් සියල්ලෙහිම අවසන්/සමක වෝල්ටියතා අගය සොයා ගෙන, එම සමක වෝල්ටියතා ප්‍රභවයෙන් ධාරාව දැන් ගමන් කරන දිශාව සොයා ගත හැකිය (ඉහත දකුනු රූපය).

කෙසේ වෙතත් මෙම නියමය යෙදීමට දිශාව කුමක් වුවත් අවසාන පිලිතුර එකම වේ; අවශ්‍ය වන්නේ නිශ්චිත දිශාවක් දිගටම සැලකීමයි. දැන් තෝරාගත් දිශාව ඔස්සේ ධාරාවක් ගලා යන්නේ යැයි සිතන්න. එම ධාරාව එක් එක් ප්‍රතිරෝධය හරහා ගලා යෑමේදී ඒ ඒ ප්‍රතිරෝධය දෙපස යම් වෝල්ටියතාවක් බැඟින් පාතනය වේ. මෙන්න මෙම වෝල්ටියතාවන් තමයි දැන් එකතු කරන්නට වන්නේ. මෙම වෝල්ටියතා පාතනයන්වල ධන හා ඍන පැති ගැන සැලකිලිමත් විය යුතුය. ධාරාවක් ප්‍රතිරෝධයක් හරහා ගලා යෑමේදී එම උපාංගය තුලට ඇතුලුවන අග්‍රය ධන ලෙසත්, ධාරාව එම උපාංගයෙන් ඉවත් වන අග්‍රය ඍන ලෙසත් සැලකේ.

වෝල්ටියතා සැපයුම්ද තිබේ නම් ඒවායේ වෝල්ටියතාවන්ද මීට එකතු වේ. එම වෝල්ටියතා සැපයුම්වලත් ධන ඍන භේදය ගැන සැලකිලිමත් විය යුතුය. උදාහරණයට ගත් ඉහත රූපයෙහි රෙසිස්ටර්වල + අග්‍රයට පසුවයි - අග්‍රය පිහිටන්නේ. රෙසිස්ටර් දෙකම මෙම රටාව අනුගමනය කරයි. එහෙත් විභව සැපයුමෙහි පලමුව – අග්‍රයත් දෙවනුව + අග්‍රයත් ලෙස රටාවට ප්‍රතිවිරුද්ධ වේ. එලෙස පරිපථයේ සලකා බලන දිශාවට ප්‍රතිවිරුද්ධව පිහිටන වෝල්ටියතාවන් - ලකුණ සහිත වේ. විභව සැපයුමක් යනු වෝල්ටියතා පාතනයක් නොවන වගද සිහි තබා ගන්න. මෙවිට ඉහත ලියා ඇති කර්චොෆ්ගේ වෝල්ටියතා නියමය අනුව, පහත ආකාරයට ප්‍රකාශයක් ලැබේ ඉහත රූපය සඳහා.

(+IR₁) + (IR₂) + (-V_S) = 0

ඉහත ප්‍රකාශය සත්‍ය යැයි ඔබට පහසුවෙන්ම පෙනේවි IR₁ + IR₂ = V_S බවට ඉහත ප්‍රකාශය පත් කර ගැනීමෙන්. එනම්, සැපයුම් විභවයෙන් සපයන මුලු වෝල්ටියතාවම රෙසිස්ටර් දෙක විසින් බෙදා ගෙන ඇත. වෝල්ටියතා සැපයුමකින් සපයන වෝල්ටියතාව මුලුමනින්ම එම පරිපථයේ පවතින “කවුරු කවුරුන්” හෝ විසින් රඳවා ගත යුතුය. පිටින් කවුරුවත් (ප්‍රතිරෝධ) සවි කර නැතිනම් (එනම් කෙලින්ම බැටරි අග්‍ර දෙක ෂෝට් කර ඇති විට), බැටරියේ අභ්‍යන්තර ප්‍රතිරෝධය විසින් බැටරියේ මුලු විභවයම තමන් දෙපස ඩ්‍රොප් කර ගනී. අභ්‍යන්තර ප්‍රතිරෝධය ඉතා කුඩා අගයක් නිසා, V=IR යන ඕම් නියමය අනුව ඉතා විශාල ධාරාවක් ගලා යයි. එවිට බැටරිය එකවර ගිනියම් වන්නට රත් වේ; ගිනි ගැනීමටත් හැකියි (පුපුරා යෑමටත් හැකියි). අන්න එමනිසයි බැටරි ෂෝට් වීම කෙසේ හෝ වැලැක්විය යුත්තේ.

ඉහත ආකාරයට රෙසිස්ටර් දෙපස ඩ්‍රොප් වන විභවයන් සියල්ලේ එකතුව එම පරිපථයේ ඇති විභව සැපයුමට සමාන කළ හැකි නිසා, සමහරුන් කර්චොෆ්ගේ වෝල්ටියතා නියමය “පරිපථයේ ඇති වෝල්ටියතා පාතනයන් සියල්ලෙහිම එකතුව ඊට සවි කර ඇති විභව සැපයුමට සමාන වේ” ලෙස ඉදිරිපත් කරයි. රෙසිස්ටර්, කැපෑසිටර්, කොයිල්, ඩයෝඩ, ට්‍රාන්සිස්ටර් සන්ධි වැනි උපාංගවල තමයි විභව පාතනයන් සිදු වන්නේ; බැටරි/වෝල්ටියතා ප්‍රභව/ධාරා ප්‍රභව යනු විභවයන් උත්පාදනය කරන ඒවාය (මේවායේ කුඩා අභ්‍යන්තර ප්‍රතිරෝධයක් ඇතත් ඒවා නොසලකා හැරේ).

දිශාව වෙනස් කළත් ගැටලුවක් නොවන බව මා පැවසුවනෙ. එය එසේදැයි දැන් බලමු. දිශාව පහත ආකාරයට වෙනස් කර ගන්න. දැන් සත්‍ය ලෙසම ධාරාවන් ගලා යන දිශාව හා අප තෝරා ගත් පුඩුවේ දිශාව එකිනෙකට ප්‍රතිවිරුද්ධ වේ. එනිසා, KVL ප්‍රකාශය (-IR₁) + (-IR₂) + (+V_S) = 0 → -IR₁ – IR₂ + V_S = 0 වේ. එය නැවතත් -IR₁ – IR₂ = -V_S → V_S = IR₁ + IR₂ බවට පත් වන අතර, මින් පෙරත් ලැබුණේ එයමයි නේද?

පහත පරිපථයේ පෙන්වා දෙන පරිදි කර්චොෆ්ගේ වෝල්ටියතා නියමය අවස්ථා කිහිපයකටම යෙදිය හැකිය. සංවෘත පරිපථය කොටසක් හෙවත් පුඩුවක් පවතින සෑම තැනකටම එය යෙදිය හැකිය. දැන් එක් එක් පුඩුවට KVL යොදමු.

r₁i₁ + r₃(i₁ + i₂) + r₄(i₁ + i₃) + (-e₁) = 0

r₁ රෙසිස්ටරය හරහා ගලා යන එකම ධාරාව i₁ වේ. එනිසා එම රෙසිස්ටරය හරහා i₁r₁ ක වෝල්ටියතා ප්‍රමාණයක් ඩ්‍රොප් වේ. එම i₁ ගලා යන පුඩුවේම ඊළඟ රෙසිස්ටරය වන r₃ හරහා i₁ ධාරාවට අමතරව i₂ ධාරාවකුත් ගලා යයි. එම ධාරා දෙකම උඩ සිට යටට එකම දිශාවට ගමන් කරන නිසා එම ධාරා දෙකෙහි එකතුවෙන් r₃ ගුණ වේ. එම i₁ පුඩුවේම ඊළඟ රෙසිස්ටරය වන e₄ හරහාත් i₁ ට අමතරව i₃ ධාරාවකුත් එම දිශාව ඔස්සේම ගමන් කරයි. එලෙස එක් එක් ධාරාවන් ගමන් කරන දිශා ගැනද සැලකිලිමත් වී පහත ප්‍රකාශ දෙකත් විශ්ලේෂනය කර බලන්න.

r₂i₂ + r₃(i₂ + i₁) + r₅(i₂ – i₃) + (-e₂) = 0

r₆i₃ + r₅(i₃ – i₂) + r₄(i₃ + i₁) = 0

බැටරිවල හා රෙසිස්ටර්වල අගයන් දී ඇති විට, ඉහත එක් එක් පුඩුව තුල ගමන් කරන ධාරාවන් සෙවිය හැකිය. මේ සඳහා ඉහත සමීකරණ 3 විසඳිය යුතුය. සමගාමී සමීකරණ හෝ න්‍යාස යන ගණිත සංකල්ප ඇසුරින් ඒවා විසඳිය හැකියි. ගණිතමය පැත්තෙන් ඒවා හොඳ ගණිත ගැටලු වුවද, පරිපථ නිර්මාණයේදී අපට ඒවා විසඳීමට එතරම් අවශ්‍ය වන්නේ නැත. ඉතා පහසුවෙන් විසඳීමට තරම් අවශ්‍ය දත්ත ප්‍රමාණයක් අපට ඉබේම ලැබේ. ප්‍රායෝගික උදාහරණයක් බලමු.

ඉහත ට්‍රාන්සිස්ටර් පරිපථයේ ඉන්පුට් කොටසට දැන් KVL යොදමු.

R_BI_B + V_BE + (-V_CC) = 0 → V_CC = R_BI_B + V_BE

ඇත්තෙන්ම මා ඉහත රූපයේ නිල්පාටින් ඇඳ ඇති ජව සැපයුම් වයරය සාමාන්‍යයෙන් පරිපථ සටහන්වල දක්වන්නේ නැත. පුඩුව පැහැදිලි වීම පිනිසයි මා එය ඇන්දේ. එනිසා එය නැතිවත් එම වයරය සිතින් ඇඳගෙන මෙම නියම යෙදීමට පුරුදු වන්න. එලෙසම, එම පරිපථයේ අවුට්පුට් කොටසටත් KVL යොදා පහත ආකාරයේ ප්‍රකාශයක් ලබා ගත හැකියි.

I_CR_C + V_CE = V_CC

මෙතෙක් මා පුඩුවක් ඇඳ හෝ සිතින් මවා ගෙන KVL යොදන අයුරුයි පෙන්වා දුන්නේ. ප්‍රායෝගිකව මීටත් වඩා පහසු ක්‍රමයක් තිබේ. එහිදී පරිපථයේ V_CC අග්‍රයෙන් පටන් ගෙන භූගතය/GND දක්වා (V_EE තිබේ නම් V_EE දක්වා) පිලිවෙලින් එක් එක් වෝල්ටියතා පාතනයන් එකින් එක අඩු කර ගෙන ගොස් අවසානයේ = 0 කරන්න.

V_CC – I_BR_B – V_BE – GND = 0

GND යනු 0 V වන නිසා, එවැනි ප්‍රකාශයක GND නොලියා සිටිය හැකියි (V_CC – I_BR_B – V_BE = 0 බවට එමඟින් පත් වේ). ඉහත ප්‍රකාශය නැවතත් V_CC = I_BR_B + V_BE ලෙස ලිවිය හැකියි නේද? මීට පෙර පුඩු ආකාරයෙනුත් ලැබුණේ එයමයි. එහෙත් මෙම ක්‍රමයේදි පුඩුවක් ලෙස සලකා නොව රේඛීය ලෙස සලකායි එය සිදු කළේ; එය පහසුවකි.

දැන් KCL ගැන බලමු. එය Kirchoff’s Point Law, Kirchoff’s Nodal Law, Kirchoff’s Junction Law ආදි නම්වලින්ද හැඳින්වේ. KVL ටත් වඩා පහසුවෙන් මෙය අවබෝධ කර ගත හැකිය. එහි නිර්වචනය පහත ආකාරයට ලිවිය හැකිය.

පර්පථයක ඕනෑම ලක්ෂ්‍යයක් සැලකුවොත්, එම ලක්ෂ්‍යයට ඇතුලුවන ධාරා හා එම ලක්ෂ්‍යයෙන් පිට වන ධාරා සියල්ලෙහිම එකතුව ශූන්‍ය වේ. ගණිතානුකූලව එය Σ I = 0 ලෙස ලිවිය හැකිය.

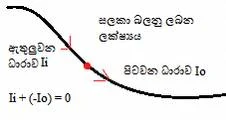
අර සලකා බලන ලක්ෂ්‍යය යම් වයරයක එක් ස්ථානයක් විය හැකිය. එවිට, වයර් එක දිගේ එක් පැත්තකින් එම ස්ථානයට ධාරාව (I_i) ඇතුලු වේ. එම ඇතුලු වෙච්ච ධාරාව ඒ ක්ෂණයෙහිම එම ලක්ෂ්‍යයෙන් ඉවත්ව වයරයේ අනෙක් පැත්තට ගලා ගෙන යයි (මෙම පිටවන ධාරාව I_o ලෙස නම් කරමු). ඒ කියන්නේ ඇතුලු වූ ධාරාව පොඩ්ඩක්වත් අඩුවක් නැතිව පිට වේ. එය ඉතිං කොහොමත් සිදු විය යුත්තක්නෙ. එනිසා I_i = I_o ලෙස ලිවිය හැකියිනෙ. එයම I_i + (-I_o) = 0 ලෙසත් ලිවිය හැකියි. මෙහිදී ලක්ෂ්‍යය තුලට ඇතුලුවන ධාරා + ලෙසද, ඉන් පිටවන ධාරා - ලෙසද සලකා ඇත (අවශ්‍ය නම්, ලක්ෂ්‍යය තුලට ඇතුලුවන ධාරා - ලෙසත්, ඉන් පිටවන ධාරා + ලෙසත් සැලකිය හැකියි).

තනි වයරයක ලක්ෂ්‍යයක් මතත් KCL යෙදිය හැකි බව දැන් පැහැදිලියි; නමුත් අප එය කරන්නේ නැහැ මොකද එය අමුතුවෙන් KCL යොදාගෙන අවබෝධ කර ගැනීමට හෝ විශ්ලේෂනය කිරීමට තරම් දෙයක් නොවන නිසා. එහෙත් හැමතිස්සේම අප KCL යොදන්නේ සන්නායක කිහිපයක් එකට එකතු වන “මංසන්දියකටය” (node). මෙවිට එම ලක්ෂ්‍යයට/මංසන්දියට විවිධ පැති/වයර් ඔස්සේ ධාරා ඇතුලු වේ හා පිට වේ.

ඉහතදී පෙන්වා දුන් ලෙස, එම ලක්ෂ්‍යයට විවිධ වයර් ඔස්සේ ධාරාවන් කොතරම් ගණනක් ඇතුලු වුවත්, එම ලක්ෂ්‍යයෙන් පිටතට විවිධ වයර් ඔස්සේ ධාරාවන් කොතරම් ගණනක් පිට වුවත්, එම “ඇතුලුවන ධාරාවන්ගේ එකතුව හැමවිටම පිටවන ධාරාවන්ගේ එකතුවට සමාන වේ”. එනිසා KCL අන්න එලෙසත් අර්ථ දැක්වේ.

ඇත්තෙන්ම කර්චොෆ්ගේ නියම දෙක සරල වුවත්, පරිපථ සැලසුම්කරණයේදී නැතිවම බැරි වටිනා නියම වේ.