සන්නිවේදනය හා ආධුනික ගුවන් විදුලි සේවය (Amateur radio) - 20

මූර්ජනය

මූර්ජනය (modulation) නොමැති වූවා නම් විදුලි සන්දේශ ක්‍රම නොපවතින්නද ඉඩ තිබුණි. එය එතරම්ම වැදගත් හා විදුලි සන්දේශයට නැතිවම බැරි ක්‍රියාවලියකි. මෙයම (සංඥා) මිශ්‍රණය (mixing) යන නමින් හැඳින්විය හැකිය. මූර්ජනය සිදු කරන පරිපථ කොටස මූර්ජකය (modulator) හෙවත් මිශ්‍රකය (mixer) ලෙස හැඳින්වේ. ඉතිං මූර්ජනය යනු කුමක්ද? ඊට අර්ථ දැක්වීම් කිහිප ආකාරයකින් කළ හැකිය. ඉතාම සරලව එය “සංඥා දෙකක් මිශ්‍ර කිරීම” ලෙස කිව හැකිය. එහෙත් ඊට වඩා සාර්ථක අර්ථ දැක්වීමක් වන්නේ “යම් තොරතුරක් සහිත අවසංඛ්‍යාත සංඥාවක් දිගු දුරකට සන්නිවේදනය කිරීම සඳහා තවත් නිශ්චිත අධිසංඛ්‍යාත සංඥාවක් සමග මිශ්‍ර කිරීම” යන්නයි. එහෙත් අර්ථ දැක්වීම කටපාඩම් කරනවාට වඩා ඉන් සිදුවන ක්‍රියාවලිය දැනගැනීම තමයි ප්‍රයෝජනවත් වන්නේ.

මූර්ජනය යන ක්‍රියාව තුල, සිදුවීම් දෙකක් එකවර සිදු වේ. මේ දෙක වෙන වෙනම ඉගෙන ගමු. ඊට පෙර ඔබ දැනගත යුතු ඉතාම වැදගත් කරුණක් ගැන විමසා බලමු.

Fourier Transformation

පරිසරයේ අපට මැනිය හැකි විවිධාකාර ගතිලක්ෂණ තිබෙනවානෙ. ඒවා කාලය සමග වෙනස් වන නිසා සංඥා ලෙස හැඳින්වෙන අතර, සුදුසු සංවේදක හෙවත් පාරනායකයක් මඟින් එම සංඥා ඊට අනුරූප විද්‍යුත් සංඥා බවට පත් කර ගත හැකි බව ඔබ දන්නවා. එවැනි විදුලි සංඥාවක් තරංග මඟින් නිරූපණය කළ හැකිද? හැකි නම්, කුමන ආකාරයේ තරංගයක් වේවිද? එම තරංගයේ සංඛ්‍යාතය කුමක් වේවිද? ඒ ගැන ඔබට දැනෙන්නේ කුමක්ද?

යම් සංඥාවක් යම් නිශ්චිත සංඛ්‍යාතයක් සහිත තරංගයක් මඟින් නිරූපණය කළ හැකි යැයි මොහොතකට සිතමු. එවිට, එම සංඥාව නිරූපණය කෙරෙන එම තරංගය සම්ප්‍රේෂනය කිරීම පමණක් ප්‍රමාණවත් වෙනවා එම සංඥාව යම් තැනකට සන්නිවේදනය කරන්නට. උදාහරණයක් ලෙස, යම් සංඥාවක් හර්ට්ස් 900ක තරංගයකින් නිරූපණය වන්නේ යැයි සිතමු. එවිට එම හර්ට්ස් 900 තරංගය අපට රේඩියෝ තරංගයක් සේ හෝ වයරයක් දිගේ විදුලි තරංගයක් සේ හෝ සම්ප්‍රේෂනය කළ හැකියි. එලෙසම තවත් සංඥාවක් හර්ට්ස් 901ක තරංගයකින් නිරූපණය කර, එයද පෙර සේම රේඩියෝ හෝ විදුලි තරංගයකින් සම්ප්‍රේෂනය කළ හැකියි පමණක් නොව, හර්ට්ස් 900 හා හර්ට්ස් 901 තරංග දෙක එකිනෙකට බාධා ඇති කර ගන්නේද නැත (මොකද ඒවා වෙන වෙනම ගමන් කරන වෙනස් සංඛ්‍යාත දෙකකින් යුතු තරංග නිසා). මෙලෙසම, හර්ට්ස් 902, 903 ආදී ලෙසද තරංග යැවිය හැකියිනෙ එකිනෙකට බාධා කර ගන්නේ නැතිව. ඒ අනුව හර්ට්ස් 900 සිට හර්ට්ස් 1000 දක්වා පමණක් විවිධ සංඥා 100ක් අපට යවන්නට තිබුණා නේද? මෙලෙස සිතා බැලුවොත් අපට කිලෝහර්ට්ස් 1 සිට ගිගාහර්ට්ස් 1 දක්වා පමණක් එකිනෙකට වෙනස් තරංග බිලියනයක් පමණ එකවර රේඩියෝ තරංග ඔස්සේ පමණක් සම්ප්‍රේෂනය කරන්නට තිබුණා. එහෙත් එය සිහිනයක් පමණි. සැබෑ ලෝකයේදී එය සිදු කළ නොහැකියි. ඒ ඇයි කියා මොහොතකින් පෙනේවි.

ඔව්, ඕනෑම විදුලි සංඥාවක් සැබෑ ලෝකයේදීත් තරංග මඟින් අනිවාර්යෙන්ම නිරූපණය කළ හැකියි. එහෙත් එම තරංගය සරල නොවේ. ඒ කියන්නේ එවැනි සංඥාවක් එක් නිශ්චිත සංඛ්‍යාතයකින් යුතු එක් තරංගයකින් පමණක් නිරූපණය කරන්නට බැරිය. සාමාන්‍ය ප්‍රායෝගික විදුලි සංඥා අක්‍රමවත් හැඩවලින් යුක්තය (ඒ කියන්නේ එය පිරිසිදු සයිනාකාර තරංග ස්වරූපයෙන් පවතින්නේ නැති බවයි). මෙවැනි අක්‍රමවත් තරංගයක් ඇත්තටම සංඛ්‍යාතයන් එකිනෙකට වෙනස් පිරිසිදු සයිනාකාර තරංග රැසකගේ එකතුවක් ලෙස නිරූපණය කළ හැකි බව ෆූරියර් (Joseph Fourier) නම් ගණිතඥයා බොහෝ කාලයකට පෙර අපට පෙන්වා දුන්නා. එය විශාල ජයග්‍රහණයකි. අක්‍රමවත් හැඩය ඇති වන්නේ ක්‍රමවත් හැඩ (එනම් සංඛ්‍යාතයන් විවිධ සයිනාකාර තරංග) කිහිපයක එකතුවකින් බවයි ඉන් කියැවෙන්නේ.

පහත රූපය බලන්න. එහි උඩින්ම තිබෙන්නේ සයිනාකාර නොවන අක්‍රමවත් තරංගයකි. එහි දෙවැනි රූපයෙන් පෙන්වා තිබෙන්නේ එම අක්‍රමවත් හැඩය සහිත තරංගය (රතු පාටින්) හා එය සෑදී තිබෙන සයිනාකාර තරංග සෙට් එකයි (නිල් පාටින්). මේ එක් එක් සයිනාකාර තරංගයේ සංඛ්‍යාතයන් මෙන්ම විස්තාරයන්ද වෙනස් බව වටහ ගන්න. ඊට යටින් ඇති රූපයෙන් මෙම සයිනාකාර තරංග සෙට් එක වෙන වෙනම දක්වා තිබෙනවා. එහි රතු පටින් ඔරිජිනල් අක්‍රමවත් සංඥාවද, වෙන වෙනම නිල් පාටින් සයිනාකාර තරංගද පැහැදිලිව දක්වා තිබෙනවා. ඒ විතරක්ද නොවේ, ඒ එක් එක් සයිනාකාර තරංගයන් වෙනම ප්‍රස්ථාර අක්ෂයක් දිගේ (නිල් පාටින්) ලකුණු කරද තිබෙනවා. අවසාන රූපයෙන් පෙන්වා තිබෙන්නේ ඉහත වෙන වෙනම සංඛ්‍යාතයන් ලකුණු කළ ප්‍රස්ථාර අක්ෂය පමණි. මෙලෙස යම් අක්‍රමවත් තරංගයක පවතින සියලු සයිනාකාර තරංග පහසුවෙන් ප්‍රස්ථාර අක්ෂයක් මත ලකුණු කළ හැකි වීම මෙම ප්‍රස්ථාරයේ ඇති ප්‍රයෝජනය වේ. එවිට, තිරස් අක්ෂය දිගේ සංඛ්‍යාතයන්ද, සිරස් අක්ෂය දිගේ ඒ එක් එක් සයිනාකාර තරංගයේ විස්තාර අගයද (එනම් අදාල සයිනාකාර තරංගයේ ප්‍රබලත්වය) දැක්විය හැකියි. තාක්ෂණයේදී නිතරම, අප මෙම සරල සංඛ්‍යාත ප්‍රස්ථාර ප්‍රයෝජනයට ගන්නවා (එය සයිනාකාර තරංග හැඩ එකින් එක අඳිනවාට වඩා ඉතා පහසුයි මොකද කෙටි ඉරි කැබැලි පමණයි දැන් ලකුණු කිරීමට තිබෙන්නේ).

සටහන

ප්‍රංශ ජාතික ෆූරියර් ජීවත් වූයේ 1800 ගණන්වලය. එකල ඔහු මෙම න්‍යාය ඉදිරිපත් කළද, ඉන් විශාල වැඩක් ගැනීමට නොහැකි විය. ඊට හේතුව වූයේ එම න්‍යාය පදනම් වූයේ තරමක් බරපතල ගණිත සූත්‍රයක් මතයි. එම සූත්‍රය පහත දැක්වේ.

ඇත්තටම පෙනුමින් එය ඒ තරම්ම බරපතල බවක් කෙනෙකුට නොපෙනෙන්නට ඉඩ තිබුණත්, ගණනය කරන විට ඒ සඳහා විශාල කාලයක් ගත වෙනවා මොකද තත්පරයක් වැනි කුඩා කාලයක් සඳහා වූ අක්‍රමවත් තරංගයක් සඳහා වුවද එම සූත්‍රය සියදහස් වතාවක් නැවත නැවත ගණනය කරන්නට සිදු වන නිසා. සාමාන්‍යයෙන් කියන්නේ එවැනි කුඩා කාලයක් පවතින සංඥාවක් සඳහා වුවද එය යම් කෙනෙකු ගණනය කරන්නට ගියොත්, ඔහුට අවුරුදු 100කට වඩා ඒ සඳහා ගත වනු ඇති කියාය.

ෆූරියර්ගේ න්‍යාය ආකාර කිහිපයකින් ඉදිරිපත් කළද හැකියි. ඉන් අපට (ඉංජිනේරුවේදයට/ඉලෙක්ට්‍රොනික්ස්/විදුලිසංදේශ) වැදගත් වන්නේ Fourier Transformation (FT) යන්නයි. මෙමඟින් පුලුවන් ඕනෑම අක්‍රමවත් හැඩයක් සහිත සංඥාවක් සංඛ්‍යාතයන් එකිනෙකට වෙනස් විවිධ සයිනාකාර තරංග ගොන්නක එකතුවක් සේ පෙන්වන්නට. යම් සංඥාවක ඇති එම සංරචක සංඛ්‍යාතයන් දැනගැනීම මඟින් අපට බොහෝ විශ්වකර්ම වැඩ කර ගත හැකියි (ඒ ගැන අවශ්‍ය නම් සොයා බලන්න).

පෙර කියූ ලෙස ආදී කාලයෙහි මෙම න්‍යාය ප්‍රායෝගිකව යොදා ගැනීමට නොහැකි වූයේ එය ඉක්මනින් සිදු කර ගැනීමට තරම් දියුණු තාක්ෂණයක් එකල නොතිබූ නිසාය. එහෙත් පසු කාලයේ පරිගනක තාක්ෂනය ඇති වී ඉතා සීඝ්‍රයෙන් දියුණු විය. එමඟින් අවුරුදු සිය ගණන් ගත වූ ගණනය කිරීම දැන් තත්පර ගණනකින් සිදු කර ගත හැකිය. විද්‍යාවේ හා තාක්ෂණයේ වෙනස වටහා ගන්නටත්, ඒ දෙකෙහි දියුණුව එකිනෙකාට බලපාන අයුරු විමසීමටත් හොඳම උදාහරණයකි මෙය. ඒ සමගම සාම්ප්‍රදායික ෆූරියර් සූත්‍රය වෙනුවට ඊට වඩා කෙටි වේලාවකින් ගණනය කළ හැකි DFT (Discrete Fourier Transformation) නම් ක්‍රමය සොයා ගත්තේය (සාම්ප්‍රදායික ෆූරියර් සූත්‍රයෙන් තමයි DFT ව්‍යුත්පන්න කර තිබෙන්නෙත්). එවැනි ප්‍රචලිත DFT ක්‍රමයක් තමයි FFT (Fast Fourier Transformation) කියා හැඳින් වන්නේ. අද හැමතැනම වාගේ භාවිතාවේ පවතින්නේ FFT වේ.

එවිට, යම් ප්‍රායෝගික සංඥාවක් සඳහා සංඛ්‍යාතයන් එකිනෙකට වෙනස් තරංග “සෙට් එකක්” අවශ්‍ය වෙනවා. බොහෝවිට මෙම තරංග සෙට් එකට විවිධ සංඛ්‍යාතයන් සහිත තරංග සිය ගණනක් හෝ දහස් ගණනක් හෝ සමහරවිට මිලියන ගණනක් අඩංගු විය හැකියි. ඒ කියන්නේ සංඥාවක් තරංග ඔස්සේ නිරූපණය කරන විට, ඒ සඳහා තනි සංඛ්‍යාතයක් නොව, සංඛ්‍යාත පරාසයක්ම අවශ්‍ය කරනවා. මොහොතකට සිතමු යම් සංඥාවක් යැවීමට එකිනෙකට ළඟින් පිහිටි (අනුයාත) සංඛ්‍යාත 100ක් අවශ්‍ය යැයි කියා. එවිට හර්ට්ස් 900 සිට හර්ට්ස් 1000 දක්වා වූ සංඛ්‍යාත සෙට් එකම එම තනි සංඥාව සඳහා යොදා ගන්නට සිදුවෙනවානෙ. ඒ කියන්නේ පෙර අවස්ථාවේ එක් සංඥාවකට හර්ට්ස් 1 බැඟින් සංඥා 100ක් යවනවා වෙනුවට දැන් යැවිය හැක්කේ එකම එක සංඥාවක් පමණි. එලෙසම, කිලෝහර්ට්ස් 1 සිට ගිගාහර්ට්ස් 1 දක්වා රේඩියෝ සංඛ්‍යාත පරාසය තුල හර්ට්ස් 100 බැඟින් සංඥා මිලියන 10ක් පමණයි දැන් යැවිය හැක්කේ (පෙර අවස්ථාවේදී එය බිලියනයක් වූවානෙ).

ප්‍රායෝගික තත්වය ඊටත් වඩා ඇත්තටම බරපතලය. පෙර කියූ ලෙසම බොහෝ සංඥා හර්ට්ස් දහස් ගණනක පරාසයක් අවශ්‍ය කරනවා. ඒ කියන්නේ එකවර යැවිය හැකි සංඥා ප්‍රමාණය අඩු වේ. උදාහරණයක් ලෙස, එක් සංඥාවකට හර්ට්ස් 10000ක හෙවත් කිලෝහර්ට්ස් 10ක සංඛ්‍යාත පරාසයක් අවශ්‍ය වේ නම්, කිලෝහර්ට්ස් 1 සිට ගිගාහර්ට්ස් 1 දක්වා වූ සංඛ්‍යාත පරාසය තුල එවැනි සංඥා ලක්ෂයක් පමණ යැවිය හැකියි. දැක්කද යම් සංඥාවක් සඳහා වැඩි සංඛ්‍යාත පරාසයක් ගන්නා විට එකිනෙකට වෙනස් සංඥා සම්ප්‍රේෂනය කළ හැකි ප්‍රමාණය තව තව අඩු වෙනවා?

එක් උදාහරණයක් සඳහා අපි බලමු කටහඬ සම්ප්‍රේෂනය කරන අවස්ථාවක්. ඔබ දන්නවා මිනිස් කන සංවේදී වන්නේ හර්ට්ස් 20 සිට හර්ට්ස් 20000 දක්වා වූ සංඛ්‍යාත පරාසයකට පමණයි. ඉතිං, කටහඬද දළ වශයෙන් එම සංඛ්‍යාත පරාසයේම පවතිනවා යනුවෙන් සිතිය හැකියි. අප කතා කරන විට විවිධ ශබ්ද පිට වෙනවානෙ. මෙම විවිධ ශබ්දවල විද්‍යුත් තරංග හැඩය බැලුවොත් පෙනේවි එම හැඩය අක්‍රමවත් බව (එනම් සයිනාකාර නොවන බව). ඒ කියන්නේ එතැන එකවර තිබෙනවා සයිනාකාර තරංග දහස් ගණනක්. පහත රූපයේ දැක්වෙන්නේ මාගේ කටින් “ක” යන ශබ්දය පරිගනකයේ මයික්‍රෆෝනයට ඇතුලු කළ විට CoolEdit නම් සොෆ්ට්වෙයාර් එකෙන් එම ශබ්දයට අදාල විද්‍යුත් සංඥා හැඩය පෙන්නුම් කරන සත්‍ය රූපයකි.

මෙම හැඩය අක්‍රමවත්ය. සයිනාකාර තරංග හැඩය පෙනෙන තෙක් මානයක නැත. ඉහත තරංගයේම පවතින විවිධ සංඛ්‍යාත පරාසයන් පහත රූපයේ දැක්වෙනවා. බලන්න එහි යටම තිරස් අක්ෂය ඔස්සේ සංඛ්‍යාත අගයන් 0Hz සිට 22000Hz දක්වා පමණ සටහන් කර තිබෙනවා. එය බැලූ විට ඔබට පෙනෙනවා ඇති, ඉහත රූපයේ පෙන්නුම් කර ඇති ක ශබ්දය සඳහා එම 0 සිට 22000 පරාසය තුල තිබෙන සියලුම සංඛ්‍යාතයන් සහභාගී වී තිබෙන බව.

සටහන

මොහොතකට සිතා බලන්න ඔබ ක හෝ ස හෝ වෙනත් ශබ්දයක් නඟන විට, එම ශබ්දයම තවත් කෙනෙකු නඟන විට, දෙදෙනාම හඬ නැඟුවේ එකම ශබ්දය වුවත් අසන කෙනෙකුට එම ශබ්ද දෙකෙහි වෙනසක් දැනෙනවානේ. මේ හඬ අහවලාගේ යැයි ඔවුන් හඳුනා ගන්නවා. එය කළ හැකි වූයේ ඉහත විස්තර කළ සිදු වීම නිසාය. සෑම ශබ්දයක්ම/සංඥාවක්ම එකිනෙකට වෙනස් සයිනාකාර තරංග සෙට් එකක එකතුවකි. එසේ වුවත්, එම සංඛ්‍යාතවල විස්තාර අගයන් හැමවිටම වෙනස් අගයන් ගනී. ඒ කියන්නේ හැඩය එකම නොවේ. මෙයම තමයි සංගීත භාණ්ඩවලත් සිදු වන්නේ. ඔබ ගිටාරයකින් රි ස්වරය වයන විට, එම රි ස්වරයම වයලීනයකින් හෝ වෙනත් සංගීත භාණ්ඩයකින් වයන විට ඒ සියල්ලම වැයුවේ එකම ස්වරය වුවත්, ඒ ඒ හඬවල විවිධත්වයක් තිබෙනවානෙ. මෙම ගුණය “ධ්වනි ගුණය” (timbre) ලෙස සංගීතයේදී/ශබ්ද විද්‍යාවේදී හැඳින් වේ (timber ලෙස එය නොලියන්න).

ඉහත සාකච්ඡාවෙන් ඔබ උගත යුතු පාඩම වන්නේ ප්‍රායෝගික සංඥාවක් තරංග මඟින් නිරූපණය කරන විට, ඒ සඳහා තරංග සංඛ්‍යාත පරාසයක්ම අවශ්‍ය කරන බව. එම සංඛ්‍යාත පරාසය සංඥාවේ සංඛ්‍යාත පරාසය හෙවත් signal bandwidth යැයි කියනවා. සාමාන්‍ය කටහඬ සඳහා හර්ට්ස් 20 සිට 20000 ක පරාසයක් අවශ්‍ය කරන නිසා, කටහඬෙහි බෑන්ඩ්විත් එක හර්ට්ස් (20000 – 20 =) 19980ක් හෙවත් දළ වශයෙන් හර්ට්ස් 20000ක් හෙවත් කිලෝහර්ට්ස් 20ක් යැයි කිව හැකියි. ලංකාවේ පවතින රූපවාහිනි තාක්ෂනය වන PAL ක්‍රමයේ වීඩියෝ සංඥාවක් සඳහා මෙගාහර්ට්ස් 6ක් හෙවත් කිලෝහර්ට්ස් 6000කට ආසන්න බෑන්ඩ්විත් එකක් අවශ්‍ය වේ (එය ශබ්දය සඳහා අවශ්‍ය බෑන්ඩ්විත් එක මෙන් 300 ගුණයක් විශාලය).

සාමාන්‍යයෙන් යම් ප්‍රභවයකින් ලබා ගන්නා සංඥාව, දුරකට සම්ප්‍රේෂනය කිරීම සඳහා විදුලි සංඥා බවට පත් කර ගන්නා විට, ඊට ස්වාභාවිකවම හිමිවන සම්පූර්ණ බෑන්ඩ්විත් එකම ලබා දෙන්නේ නැත. ඒ වෙනුවට එම සන්නිවේදන පරිපථ නිර්මාණය කරන අය තීරණය කරනවා ගැටලුවක් නොවී අවශ්‍ය වැඩේ කර ගැනීමට පමණක් ප්‍රමාණවත් තරම් බෑන්ඩ්විත් එක කොපමණද කියා. ඊට හේතුව පැහැදිලියිනෙ. බෑන්ඩ්විත් එක වැඩි විට, වටිනා මෙන්ම සීමිත සම්පතක් වන සංඛ්‍යාත කලාපය තුල එකවර පවත්වාගෙන යා හැකි සේවා ගණන (එනම් එකවර යැවිය හැකි සංඥා ගණන) අඩු වෙනවා. අපට හැකියි නම්, එක් සංඥාවක් සඳහා ලබා දෙන බෑන්ඩ්විත් එක අඩු කරන්නට, ඒ කියන්නේ බොහෝ සංඥා ප්‍රමාණයක් දැන් අපට යැවිය හැකි වෙනවා. එය උපමාවකින් කියන්නේ නම්, බසයක සීට් පේලියක වැඩි පිරිසක් වාඩි කළ හැකි නම්, ඒ කියන්නේ මගීන් බොහෝ දෙනෙකුට හිඳගෙන යෑමට ඉන් හැකි වෙනවානෙ.

ඒ විතරක්ද නොවේ, බෑන්ඩ්විත් එක අඩු කරනවා යනු, එම සංඥාව සඳහා වැය කරන විදුලි ශක්ති ප්‍රමාණයද අඩු වෙනවා යන්නයි. උපමාවකින් කියන්නේ නම්, යම් වාහනයක් විශාල වන විට, එම වාහනය සඳහා වැඩිපුර තෙල් ගාන්නටත් සිදු වෙනවා නේද? ඊටත් අමතරව තවත් තාක්ෂණික වාසි තිබෙනවා සංඥා බෑන්ඩ්විත් අඩු වීම නිසා ලැබෙන. ITU ආයතනයේ නිර්දේශය වන්නේ පුලුවන් තරම් අවම සංඥා බෑන්ඩ්විත් එකක් භාවිතා කරන ලෙසයි. මෙම සංඥා බෑන්ඩ්විත් එක සම්බන්දයෙන් ITU විසින් අනුමත කරන ලද රෙගුලාසි (RadioRegulations – RR) කිහිපයක් මා උපුටා දක්වන්නට කැමැතියි.

“1.152 necessary bandwidth: For a given class of emission, the width of the frequency band which is just sufficient to ensure the transmission of information at the rate and with the quality required under specified conditions.” මින් කියන්නේ යම් සංඥාවක් රේඩියෝ තරංග මඟින් සන්නිවේදනය කරන විට, එම සංඥාව නැවත තේරුම් ගැනීමට හැකි පරිදි සන්නිවේදනය කිරීමට තරම් ප්‍රමාණවත් සංඥා බෑන්ඩ්විත් එක necessary bandwidth ලෙස හඳුන්වන බවයි (අනවශ්‍ය තරමේ ඉතා හොඳ කොලිටියක් පසු පස නොයන ලෙස ඉන් ඉඟි කරයි).

“3.4 To the maximum extent possible, equipment to be used in a station should apply signal processing methods which enable the most efficient use of the frequency spectrum in accordance with the relevant ITU-R Recommendations. These methods include, inter alia, certain bandwidth expansion techniques, and in particular, in amplitude-modulation systems, the use of the single-sideband technique.” මින් කියන්නේ මොන “දහම් ගැට ගසා” හරි හැකිතරම් අවම බෑන්ඩ්විත් එකක් යොදන්නට කටයුතු කරන ලෙසයි. මේ සඳහා DSP භාවිතා කරන ලෙස පැහැදිලිව සඳහන් කර තිබේ.

“3.9 The bandwidths of emissions also shall be such as to ensure the most efficient utilization of the spectrum; in general this requires that bandwidths be kept at the lowest values which the state of the technique and the nature of the service permit. Appendix 1 is provided as a guide for the determination of the necessary bandwidth.” නැවතත් කියන්නේ සංඥා සඳහා හැකි තරම් අවම බෑන්ඩ්විත් එකක් භාවිතා කරන ලෙසයි.

ඒ විතරක්ද නොව, මෙම රේඩියෝරෙගුලාසිවල බොහෝ සේවා සඳහා යොදා ගත යුතු සංඥා බෑන්ඩ්විත් අගයන්ද නිර්දේශ කර තිබේ. එතරම්ම සංඥා බෑන්ඩ්විත් කාරණය බරපතලව සිතිය යුතු බව සිහිතබා ගන්න.

එහෙත් එක් ප්‍රශ්නයක් තිබෙනවා. කෘතිම විදියට (එනම් ඉලෙක්ට්‍රොනික් සර්කිට් යොදා ගෙන) සංඥාවකට හිමි ස්වාභාවික සංඛ්‍යාත පරාසය අඩු කරන විට, එම සංඥාව යම් විකෘතියකට ලක් වෙනවා. සංඥාව අතුපතර හොඳින් විහිදී ගිය දැවැන්ත ගසකට උපමා කළ හැකියි. ගස විසින් ගන්නා ඉඩ ප්‍රමාණය අඩු කරන්නට කියා ඔබට ගසෙහි විහිදුනු අතු කපා දැමිය හැකියි. ගස කෙට්ටු වේවි. එහෙත් ඒ සමගම ගස තිබුණාට වඩා වෙනස් හැඩයක් ගනීවි (ඒ කියන්නේ ගස විකෘති වෙලා). සංඥා ගැනද එසේ සිතන්න. සමහරවිට කුඩා හෝ විකෘතියක් හෝ සිදු නොවිය යුතු අවස්ථා තිබිය හැකියි. එවන් විටක, අමුතුවෙන් බෑන්ඩ්විත් එක අඩු නොකර සම්පූර්ණ සංඛ්‍යාත පරාසයම සම්ප්‍රේෂනය කළ යුතුය. එහෙත් සමහර අවස්ථා තිබෙනවා ගැටලුවක් නොවන මට්ටමක් දක්වා විකෘතිය වීමට අවසර තිබෙන සේ සංඛ්‍යාත පරාසය අඩු කළ හැකියි. කටහඬ සම්ප්‍රේෂනයේදී මෙලෙස බෑන්ඩ්විත් අඩු කිරීම හැමවිටම සිදු වේ. උදාහරණයක් ලෙස, ඔබ භාවිතා කරන රැහැන් දුරකතනවල සම්ප්‍රේෂනය වන කටහඬ සඳහා ලබා දී තිබෙන්නේ හර්ට්ස් 4000ක් තරම් කුඩා ප්‍රමාණයකි (එය කටහඬ සඳහා හිමි ස්වාභාවික සංඛ්‍යාත පරාසයෙන් පහෙන් එකක් තරම් අඩු ප්‍රමාණයකි). එනිසයි, ටෙලිෆෝනයකින් කතා කරන විට, කටහඬ වෙනස්ව ඇසෙන්නේ. කටහඬෙහි ඇතිවන එම කොලිටියේ අඩු වීම තමයි සිදු වූ විකෘතිය.

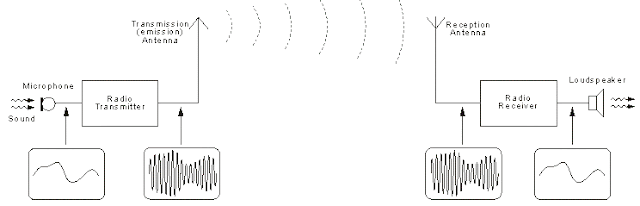
අපි දැන් මූර්ජනය ගැන බලමු. සන්නිවේදනය කිරීමට අවශ්‍ය තොරතුර සහිත සංඥාව (data/information signal) හෙවත් “බුද්ධි සංඥාව” (intelligence signal) සාමාන්‍යයෙන් හර්ට්ස් හෝ කිලෝහර්ට්ස් කිහිපයක අඩු සංඛ්‍යාත විදුලි සංඥාවක් (low frequency signal) වශයෙනුයි පවතින්නේ. උදාහරණයක් ලෙස, ඔබ කතා කරන විට ඇති වන ශබ්ද තරංගය ඊට අනුරූප විදුලි සංඥාවක් බවට මයික් එකක් මඟින් පත් කරන විට අපට ලැබෙන්නේ මෙවැනි අවසංඛ්‍යාත බුද්ධි සංඥාවකි (ඉහත විස්තරය අනුව, තනි සංඛ්‍යාතයක් නොව සංඛ්‍යාත පරාසයකින් එය යුක්ත වේ). එහෙත් සමහර උපකරණවලින් අපට මෙගාහර්ට්ස් කිහිපයක අධිසංඛ්‍යාත විදුලි සංඥාද (high frequency signal) ලැබෙන බව අමතක නොකළ යුතුය. උදාහරණයක් ලෙස, කැමරාවකින් ලැබෙන සංඥාවක් මෙගාහර්ට්ස් කිහිපයක සංඛ්‍යාත පරාසයකින් යුක්ත විය හැකියි. අවසංඛ්‍යාත වේවා අධිසංඛ්‍යාත වේවා, මෙවැනි සංඥා baseband signal ලෙස හැඳින්වේ. මෙවැනි බේස්බෑන්ඩ් සංඥා තවම මූර්ජනය කර නොමැති “ඔරිජිනල්” සංඥාය. යම් පාරනායකයකින් (tranducer) ලැබෙන සංඥා හැමවිටම බේස්බෑන්ඩ් සංඥා ලෙස සැලකිය හැකියි.

එහෙත් මූර්ජනය කිරීමේදී බේස්බෑන්ඩ් සංඥාවේ සංඛ්‍යාතයට වඩා බොහෝවිට සිය හෝ දහස් ගුණයකටත් වඩා වැඩි අධිසංඛ්‍යාත සංඥාවක් බවට එය පත් වේ. ඉතිං, මෙම ඉතා අධි සංඛ්‍යාතයට සාපේක්ෂව බලන විට බේස්බෑන්ඩ් සංඥාවේ සංඛ්‍යාතය ඉතා කුඩයි නේද (සිය දහස් ගුණයකින්)? එනිසයි මූර්ජන නිර්වචනයේ තිබුණේ “අවසංඛ්‍යාත තොරතුරු සංඥාවක් නිශ්චිත අධිසංඛ්‍යාත සංඥාවක් සමඟ මිශ්‍ර කරනවා” කියා.

බේස්බෑන්ඩ් සංඥා විදුලි සන්දේශවලදී එලෙසම සම්ප්‍රේෂනය කරවන්නේ නැත. එහෙත් සාමාන්‍ය ඉලෙක්ට්‍රොනික් පරිපථ තුල නම් සංඥා ගමන් කරන්නේ බේස්බෑන්ඩ් සංඥා ලෙසමයි. එවිට එම සම්ප්‍රෙෂනය baseband transmission ලෙස හැඳින්වේ. උදාහරණයක් ලෙස, මයික් එකකින් ලැබෙන දුර්වල බේස්බෑන්ඩ් සංඥාව වර්ධකයට යවන්නේ බේස්බෑන්ඩ් සංඥාවක් ලෙසමයි. ඉන්පසු වර්ධනය වූ බේස්බෑන්ඩ් සංඥාව පරිපථයේ වෙනත් කොටස් හරහා ගමන් කරන්නේද බේස්බෑන්ඩ් සංඥාවක් ලෙසමයි.

සාමාන්‍ය පරිපථයක් තුල බේස්බෑන්ඩ් සංඥා ගමන් කරන්නට සැලස්සුවත්, දිගු දුරකට baseband transmission යොදා ගන්නේ නැත්තේ ඇයි? මෙම ප්‍රශ්නයට පිළිතුර ලෙස අවසානයේ ලැබෙන්නේ මූර්ජනයේ අවශ්‍යතාවයි. උදාහරණයකින් එය විමසා බලමු. සිතන්න ඔබ හා ඔබේ යෙහෙලිය අතර සංවාදයක් (සන්නිවේදනයක්) සිදු වෙනවා කියා යම් තැනක. ඔබේ කට විසින් නිපදවන ශබ්ද හැමවිටම හර්ට්ස් 20ත් 20000ත් අතරනෙ (ඒ කියන්නේ හර්ට්ස් 20000ක බෑන්ඩ්විත් එකක් සහිත සංඥාවකි කටහඬ). එය ඇයට ඇසේවි ඉතා හොඳින්. දැන් ඔබලා දෙදෙනා සිටින්නේ කිලෝමීටර් ගණනක් ඈතින් නම් කෙලින්ම කටහඬින් සන්නිවේදනය කිරීමට බැරි නිසා, විදුලි සන්දේශ ක්‍රමයක් භාවිතා කිරීමට සිදු වෙනවා. සිතන්න ඒ සඳහා යොදා ගන්නේ රේඩියෝ තරංග කියා. ඒ අනුව ඔබේ කටහඬ මයික් එකක් හරහා ඊට අනුරූප විදුලි සංඥාවක් බවට පළමුව පත් කරගැනීමට සිදු වේ. එවිට එම විදුලි සංඥාවද පවතින්නේ හර්ට්ස් 20ත් 20000ත් අතරනෙ. දැන් එම විදුලි සංඥාව තවදුරටත් වර්ධනය කර, කෙලින්ම ඇන්ටනාවකට යොමු කළ විට, ඇන්ටනාව මඟින් එම සංඛ්‍යාත පරාසයෙන්ම යුතු රේඩියෝ තරංග නිපදවා, ඔබේ යෙහෙලිය වෙතටද ගමන් කරාවි. මෙම ක්‍රමයත් ඉහතදී පැහැදිලි කළ පරිපථ තුල පැවති බේස්බෑන්ඩ් ට්‍රාන්ස්මිෂන් ක්‍රමයම තමයි (පරිපථය තුල බේස්බෑන්ඩ් සංඥාව විදුලි සංඥාවක් ලෙසද, දැන් එය රේඩියෝ සංඥාවක් ලෙසද සම්ප්‍රේෂනය වේ).

එහෙත් ඉහත ක්‍රමය ඉතාම අකාර්යක්ෂම වේ. ඊට හේතු කිහිපයක් ඇත. එක් සරල හේතුවක් නම්, අවසංඛ්‍යාත සඳහා රේඩියෝ තරංග නිපදවීම කිසිසේත් පහසු නැත. ඒ සඳහා සමහරවිට කිලෝමීටර් ගණන් දිගු ඇන්ටනා සෑදීමට සිදු වේවි. තවද, ඒ සඳහා අතිවිශාල වොට් ගණනකින් යුතු විදුලි බලයක්ද වැය වේවි (මොකද එච්චරට අකාර්යක්ෂමයි අවසංඛ්‍යාත සම්ප්‍රේෂක). කෙසේ හෝ එම අවාසි විඳ දරාගෙන සිටියත් එක් අවාසියක් තිබෙනවා නිකංම විඳ දරාගෙන සිටිය නොහැකි. ඒ කුමක්ද?

සිතන්න දැන් ඔබ සිටින ප්‍රදේශයේම තවත් කෙනෙකුටත් ඔහුගේ මිතුරෙකුට කතා කරන්නට අවශ්‍යයි කියා. එවිට ඔහුද ඉහත ආකාරයටම බේස්බෑන්ඩ් ට්‍රාන්ස්මිෂන් එකක් සිදු කළොත්, ඔබේ හා ඔහුගේ රේඩියෝ සංඥා දෙකම එකම සංඛ්‍යාත කලාපය තුල පවතින නිසා, එම රේඩියෝ සංඥා එකිනෙකට මිශ්‍ර වී විකෘති (interference) වේවි. එලෙස තව තවත් අයත් කතා කළොත් එය එකම ඝෝෂාකාරි ශබ්දයක් ලෙස ඇසේවි හරියට කලබලකාරී වෙලාවක බොහෝ දෙනා කතා කරන නිසා ඇතිවන ඝෝෂාව මෙන් (ඉරිද පොල වගේ).

ඉහත ආකාරයට සංඥා විකෘතිය (ඝෝෂාව) ඇති වූයේ සියලුම සංඥා “එක ගොඩේට” (එකම සංඛ්‍යාත පරාසය තුල) ගමන් කළ නිසාය. සාමාන්‍ය පරිපථයකදී ගමන් කරන්නේ එකම සංඥාවක් බැවින් එය ගැටලුවක් ඇති නොකරන නිසයි සාමාන්‍ය පරිපථ තුලදී සංඥා බේස්බෑන්ඩ් ක්‍රමයට ගමන් කරවූයේ. එහෙත් විදුලි සංදේශ යනු එකවර විශාල පිරිසක් පරිහරණය කරන දෙයකි. එනිසා ඉහත පැහැදිලි කළ ලෙසට බේස්බෑන්ඩ් ක්‍රමය කිසිසේත්ම යොදා ගත නොහැකිය. මීට විසඳුම වන්නේ එක් එක් සංඥාව වෙනස් වෙනස් සංඛ්‍යාත පරාස තුල ගමන් කරවීමයි.

ඉහත රූපයේ ආකාරයට එක් එක් සංඥාව සඳහා වෙන වෙනම සංඛ්‍යාත පරාස ලබා දීම මූර්ජනයේදී ඉබේම සිදු වේ. එය මූර්ජනයේ එක් කාර්යකි. උදාහරණයක් ලෙස, ඔබ හා මිතුරියගෙහි සන්නිවේදනය මෙගාහර්ට්ස් 1 හෙවත් කිලෝහර්ට්ස් 1000 සිට මෙගාහර්ට්ස් 1.02 හෙවත් කිලෝහර්ට්ස් 1020 දක්වා සංඛ්‍යාත පරාසයට “ඔසවා” තබනවා මූර්ජන පරිපථය (මූර්ජකය) මඟින්. මෙහිදී කටහඬ සඳහා සම්පූර්න සංඛ්‍යාත පරාසයම (හර්ට්ස් 20000ක්) යොදා ගෙන ඇත. කිලෝහර්ට්ස් 1020න් කිලෝහර්ට්ස් 1000 අඩු කළ විට කිලෝහර්ට්ස් 20ක් හෙවත් හර්ට්ස් 20000ක් ලැබෙන නිසා කටහඬෙහි සම්පූර්ණ පරාසයම යොදා ගත් බැව් ඔබට පැහැදිලියි නේද? එලෙසම තවත් දෙදෙනෙකු අතර සිදු වන සන්නිවේදනය මෙගාහර්ට්ස් 1.02 සිට මෙගාහර්ට්ස් 1.04 දක්වා සංඛ්‍යාත කලාපයට ඔසවා තැබිය හැකියි. තවත් එවැනිම සන්නිවේදනයක් මෙගාහර්ට්ස් 1.04 සිට 1.06 දක්වා වූ කලාපය තුල තැබිය හැකියි. මෙලෙස එක් එක් සන්නිවේදනය සඳහා වෙන වෙනම සංඛ්‍යාත පරාස ලබා දිය හැකියිනෙ.

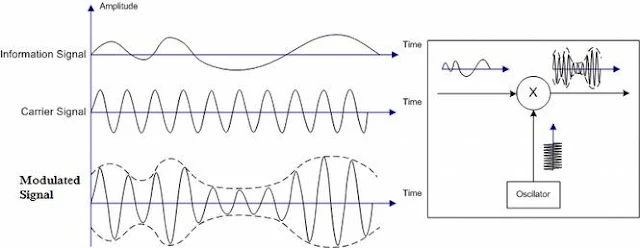
දැන් එක් ගැටලුවක් නිරාකරණය විය. එහෙත් තවමත් සියල්ල අවසන් නැත. අපට අවශ්‍ය වෙනවා තොරතුරු/බුද්ධි සංඥාව නිශ්චිත අධිසංඛ්‍යාත තරංගය තුලට කාවද්දන්නට. ඔබ සතුව ඇති යම් පනිවුඩයක් දුර තැනකට යවන විට, එය කාගෙ හරි අතේ යැවිය හැකියිනෙ. අන්න එලෙසම, බුද්ධි සංඥාව ඈතට සම්ප්‍රේෂනය කරන විට, එය “තවත් කාගේ හරි අතේ” යැවිය යුතුය. එම කෙනා වාහකයා (carrier) ලෙස හඳුන්වනවා. ඇත්තෙන්ම, වාහකයා යනුද තවත් විදුලි සංඥාවකි. එහෙත් එහි කිසිදු තොරතුරක් නැත (නිකංම හිස් කඩදාසියකට උපමා කළ හැකියි). එය නිකංම පිරිසිදු අධිසංඛ්‍යාත සයිනාකාර තරංගයකි. මෙම අධිසංඛ්‍යාත වාහක තරංගය තුලට කෙසේ හෝ බුද්ධි සංඥාව “කාවැද්දිය” යුතුය. එය කරන මූලික ආකාර 3ක් තිබේ. මෙම කුමන ආකාරයකින් හෝ බුද්ධි සංඥාව වාහක සංඥාව තුලට කාවැද්දීම තමයි මූර්ජනයෙන් සිදුවන කාරණා දෙකෙන් දෙවැනි කාරණය. බොහෝ අයට මූර්ජනය යන්න ඇසෙන විටම සිහිපත් වන එකම කාරණයද මෙයයි.

දැන් අපට තරංග වර්ග දෙකක් හමුවෙනවා. එකක් සුපුරුදු ලෙසම බුද්ධි සංඥාවයි (information signal). එය ඉතිං අපට භාහිර යම් සංවේදක පරිපථයක් මඟින්නෙ ලැබෙන්නේ. දෙවැනි තරංගය අප විසින් කෘත්‍රිමව සාදා ගන්නා පිරිසිදු සයිනාකාර වාහක තරංගයකි (carrier signal). හැමවිටම එය අධිසංඛ්‍යාත තරංගයකි. සයිනාකාර තරංගයක් නිපදවීමට භාවිතා කරන්නේ ඉතා සරල ඉලෙක්ට්‍රොනික් පරිපථයකි (ඊට කැපෑසිටරයක් හා කොයිලයක් පමණක් වුවද ප්‍රමාණවත්ය). එම පරිපථ කොටස දෝලකය (oscillator) ලෙස හැඳින්වෙනවා. එය අපගේ පරිපථය විසින්ම (එනම් අපගේ පරිපථය අසලම) නිපදවෙන නිසා ඊට Local Oscillator (LO) කියාද කියනවා. ඉතිං මෙම ලෝකල් ඔසිලේටරයෙන් නිපදවනු ලබන අධිසංඛ්‍යාත වාහක තරංගය සමගයි දැන් බුද්ධි සංඥාව මිශ්‍ර කරන්නේ. මෙම ක්‍රියාව කැටි සටහනක් (block diagram) එකක් වශයෙන් පහත ආකාරයට ඇඳ දැක්විය හැකියි. මිශ්‍ර කිරීමෙන් පසු අපට ලැබෙන්නේ මූර්ජිත සංඥාව (modulated signal) වේ. වාහක තරංගය මූර්ජනයට භාජනය කරන නිසා බුද්ධි සංඥාවටම මූර්ජක සංඥාව (modulating signal) කියාද කියනවා.

ඕනෑම තරංගයක් ගතහොත් එම තරංගයට විස්තාරයක්, සංඛ්‍යාතයක්, හා කලාවක් (phase) තිබේ. මෙම ගතිලක්ෂණ 3ම තරංගයක විචලනය වන හෝ විචලනය කළ හැකි ගුණ 3කි. ඒ සඳහා ඉලෙක්ට්‍රොනික් පරිපථ තිබේ. ඒ කියන්නේ ඔබට අවශ්‍ය නම්, යම් විදුලි තරංගයක විස්තාරය ඔබට ඕන ඕන විදියට වෙනස් කළ හැකියි. එලෙසම සංඛ්‍යාතය හා කලාවද වෙනස් කළ හැකියි. ඉතිං, අපි දැන් කරන්නේ බුද්ධි තරංගයේ විස්තාර අගයට (එනම් බුද්ධි තරංගයේ වෝල්ට් ගණනට) අනුරූපව වාහක තරංගයේ ඉහත එක් තෝරාගත් ලක්ෂණයක් විචලනය කිරීමයි. ඒ අනුව පහත දැක්වෙන ලෙස ප්‍රධාන මූර්ජන විධි 3ක් තිබේ.

1. විස්තාර මූර්ජනය (Amplitude Modulation – AM) – මෙහිදී බුද්ධි සංඥාවේ අගයට හෙවත් වෝල්ටියතාවට (හෙවත් විස්තාර අගයට) අනුරූපව වාහක තරංගයේ විස්තාරය විචලනය කරවයි.

2. සංඛ්‍යාත මූර්ජනය (Frequency Modulation – FM) – මෙහිදී බුද්ධි සංඥාවේ අගයට අනුරූපව වාහක තරංගයේ සංඛ්‍යාතය විචලනය කරවයි.

3. කලා මූර්ජනය (Phase Modulation – PM) – බුද්ධි සංඥාවේ අගයට අනුරූපව වාහක තරංගයේ කලාව විචලනය කරවයි.

සටහන

මීට පෙර, ඔබ තරංගයක සංඛ්‍යාතය, විස්තාරය ගැන ඉගෙන ගත්තත් මෙතෙක් තරංගයක කලාව ගැන අප කතා කර නොමැත. තරංගයක කලාව යනු කුමක්ද? (එය සංගීතය, නැටුම්, චිත්‍ර යන ඒවා හඳුන්වන කලාව සමග පටලවා ගන්න එපා; මේ කියන්නේ එවැනි කලාවන් ගැන නොවේ). එහෙත් විදුලි බලය ගැන කතා කරන විට තෙකලා විදුලිය (3-phase electiricity) යන වචනයේ හමුවන්නේ අප මේ ඉගෙන ගන්නට යන කලාව ගැන තමයි. කෙටියෙන් කිව්වොත් කලාව (phase) යනු තරංග දෙකක් අතර පවතින කෝණ වෙනසයි. එය තවදුරටත් සොයා බලමු.

සයිනාකාර තරංග දෙකක් එකට අඳිමු. මෙවිට, තරංග දෙකම එකම සංඛ්‍යාතයේ නම්, එම තරංග දෙකම එක විටම 0 සිට පටන් ගෙන එකම තාලෙට (ඒ කියන්නේ එකට) ගමන් කරන්නේ නම් එවිට අපි කියනවා එම තරංග දෙක අතර කලා වෙනස 0යි කියා. (පහත A රූපය). එහෙත් එක් තරංගයක් ගමන් කිරීම අරඹා යම් පමාවකට පසුව අනෙක් තරංගය පටන් ගත හැකියි. එවිට, තරංග දෙක අතර යම් කලා වෙනසක් තිබේ යැයි අප කියනවා (පහත B හා C රූප).

මෙම කලා වෙනස සාමාන්‍යයෙන් කෝණයක් ලෙසයි දක්වන්නේ. ඊට හේතුව තරංගයක් ගතහොත් එහි තිරස් අක්ෂයෙන් කෝණ අගය නිරූපණය කරන නිසාය. තරංගයක් යනු කෝණය අංශක බිංදුවේ සිට අංශක 360 දක්වා වූ පරාසයක ගමන් කරන දෙයක්නෙ. ඊටත් අමතරව, කලා වෙනස තරංග ආයාමය (λ) ආශ්‍රයෙනුත් දැක්විය හැකියි. එක් තරංග ආයාමයක් යනු අංශක 360කි (එනම් එක් සම්පූර්ණ තරංගයක්). තරංග ආයාමයෙන් භාගයක් යනු අංශක 180ද, තරංග ආයාමයෙන් කාලක් යනු අංශක 90 ද ආදී ලෙස සිතා ගත හැකියිනෙ.

යම් තරංග දෙකක් අතර කලා වෙනස අංශක 180ක් නම්, එම තරංග දෙක සම්පූර්ණයෙන්ම එකිනෙකට ප්‍රතිවිරුද්ධ තරංග දෙකක් ලෙස සලකනවා. එලෙසම, එම තරංග දෙක අතර කලා වෙනස අංශක 360ක් නම් (ඒ කියන්නේ තරංග ආයාම එකකට පසුව), එම තරංග දෙක ඇත්තටම එක උඩ එක පිහිටනවා. ඒ කියන්නේ කලා වෙනස 0 වෙනවා. ඉතිං අංශක 0ත් 360ත් අතර අගයක කලා වෙනසක් තමයි හැමවිටම පවතින්නේ.

දැන් අපි එක් එක් මූර්ජන ක්‍රමය ගැන වෙන වෙනම අධ්‍යනය කරමු.