සන්නිවේදනය හා ආධුනික ගුවන් විදුලි සේවය (Amateur radio) 17

ඩිජිටල්කරණය (Digitalization)

පරිගනක තාක්ෂණය සන්නිවේදනය හා මුසු වීම නිසා, සන්නිවේදනය ඩිජිටල්කරණය විය. ඩිජිටල්කරණය යනු සාමාන්‍ය (ඇනලොග්) සංඥා/දත්ත ඩිජිටල් සංඥා බවට පත් කිරීමයි. ඩිජිටල් දත්ත/සංඥාවල විශේෂිත වාසි තිබෙනවා සාමාන්‍ය (ඇනලොග්) සංඥා/දත්තවලට වඩා. එනිසා සන්නිවේදනය පමණක් නොව, තාක්ෂණික ලෝකයේ බොහෝ දේවල් ඩිජිටල්කරණයට හසු විය. ඩිජිටල්කරණයේ වාසි දැනගැනීමට පෙර ඇනලොග් හා ඩිජිටල් යන දෙකෙහි වෙනස වටහගත යුතුය.

ඇනලොග් (analog) හෙවත් ප්‍රතිසම සංඥාවක් යනු සලකා බලනු ලබන යම් ලක්ෂණයක යම් උපරිම හා අවම සීමා දෙකක් අතර සන්තතික විචලනය වීමකි. ඒ කියන්නේ උපරිම හා අවම අගයන් දෙක අතර පරතරය අපට බෙදිය හැකියි අනන්ත ගණනකට. ඩිජිටල් (digital) හෙවත් සංඛ්‍යාංක සංඥා යනු සලකා බලනු ලබන යම් ලක්ෂණයක යම් උපරිම හා අවම සීමා දෙකක් අතර නිශ්චිත ප්‍රමාණවලින් පමණක් විචලනය වීමකි. මෙම නිශ්චිත ප්‍රමාණය (පියවර ගණන) 2, 3, 4, 5, 100, 1000 ආදී ලෙස විය හැකිය. මෙම පියවරවල් ගණන කුඩා වුවත් ඉතා විශාල වුවත් කම් නැත; අවශ්‍ය වන්නේ අනන්ත පියවරවල් ගණනක් නොව, යම් නිශ්චිත සංඛ්‍යාවකින් කිව හැකි අගයක් (පියරවර ගණනක්) වීම පමණයි. මෙම ඇනලොග් හා ඩිජිටල් අවස්ථා දෙක පහත රූපයේ දැක්වෙන පඩි පෙල හා රෑම්ප් එකෙන් ආදර්ශනය කළ හැකියි.

රෑම්ප් එකේ ඔබ ඇවිදගෙන යන විට ඔබ දැන් සිටින තැන සිට ඊළඟට පය තැබිය හැක්කේ කොතැනකටද? ඔබට කැමති දුරකින් පය තිබිය හැකියි නේද? ඒ කියන්නේ පියවරවල් දෙකක් අතර පරතරය නිශ්චිත නැත. එලෙස පය තැබිය හැකි දුර දැන් සිටින තැන සිට අඩියක් දුරට හෝ අඩි 3ක් දුරට හෝ සෙන්ටිමීටරයක් හෝ මිලිමීටරයක් හෝ විය හැකියිනෙ. මෙය ඇනලොග් තත්වයයි. එහෙත් පඩිපෙල ගතහොත්, ඔබ දැන් සිටින පඩියේ සිට ඊළඟට අඩිය තබන්නට බැහැ ඔබට කැමති කැමති තැනකට. අනිවාර්යෙන්ම පඩි පෙළහි ඊළඟ පඩියට හෝ පඩි දෙකක් (හෝ පඩි කිහිපයක්) ඈතින් පමණයි පය තැබිය හැක්කේ. ඒ කියන්නේ පියවරවල් දෙකක් අතර පරතරය නිශ්චිතයි. උදාහරණයක් ලෙස පඩි දෙකක් අතර දුර අඩි භාගයක් නම්, ඔබට කිසිසේත් අඩි කාලක් දුරකින් අඩිය තබන්නට බැහැනෙ. මෙය ඩිජිටල් තත්වයකි.

දැන් අපි බලමු මෙම ඇනලොග් හා ඩිජිටල් තත්වයන් විදුලි සංඥාවකට ආදේශ කර. ඔබේ කටහඬ මයික් එකක් හරහා යන විට ලැබෙන විදුලි සංඥාව ගැන සිතන්න (පහත රූපය). මෙහිදී විදුලි සංඥාවේ අවස්ථා දෙකක් (එනම් වෝල්ටියතා අගයන් දෙකක්) සලකන්න. දැන් බලන්න එම වෝල්ටියතා පරාසය විචලනය වන අයුරු. එක් අගයක් වෝල්ට් 3කි. අනෙක් අවස්ථාවේ අගය වෝල්ට් 5කි. මෙම වෝල්ට් 3 සිට 5 දක්වා විචලනය වීම අඛණ්ඩව හෙවත් සන්තතිකව (continuous) පවතින බව පෙනේ. ඒ කියන්නේ එකවර වෝල්ට් 3 සිට 5ට පැන්නේ නැත. කෙනෙකුට පැවසිය හැකියි පළමුව වෝල්ට් 3.1ද ඊළඟට 3.2ද ආදී වශයෙන් වෝල්ට් 0.1 බැඟින් වැඩි වී 5 මට්ටමට පැමිණියා කියා. එහෙත් එසේ සිතීමත් වැරදියි මොකද තවත් කෙනෙකුට පරතරය ඊටත් කුඩා වෝල්ට් 0.01 බැඟින් වැඩි වූවා යැයි සිතිය හැකියිනෙ (එවිට 3.01, 3.02, 3.03 ආදී ලෙස වැඩි වේවි). තවත් කෙනෙකු 0.001ද තවත් කෙනෙකු 0.0001 බැගින්ද ගත හැකියි. මෙහි ඉවරයක් නැහැනෙ. එය තමයි ඇනලොග් සංඥාවක ලක්ෂණය. උපරිමය හා අවමය අතර විචලනය සන්තතික වීමයි (එක් අගයක සිට තවත් අගයකට පවතින පරතරය නිශ්චිත නැති අතර අපට ඕනෑම තරම් කුඩා අගයක් ඒ සඳහා ගත හැකිය).

සාමාන්‍ය ලෝකයේ සියල්ලම පාහේ ඇනලොග් වේ. ඒ අනුව, මේ විශ්වයම ඇනලොග් විශ්වයකි. ඔබ සහ ලොව සියල්ලම වයසට යන්නේ ඇනලොග් ක්‍රමයටයි. ඔබ වයසට යන්නේ අවුරුද්දෙන් අවුරුද්දට නොව, සෑම නිමේෂයක් පාසාම ඔබ වයසට යනවා. කාලය යනුද ඇනලොග් තත්වයකි (එය සන්තතිකව ගලා යනවා). ගසක හෝ ඔබේ උස යෑම, ඔබේ පෙනුමේ හෝ ලොව ඕනෑම දෙයක වෙනස් වීම, ඔබේ කටහඬ, ආලෝකය, සුළඟ, සඳ ගමන් කිරීම ආදි ලෙස ඔබේ සිතට නැඟෙන සෑම දෙයක්ම පාහේ ඇනලොග් අවස්ථා බව තර්ක කළ හැකියි පහසුවෙන්ම මොකද ඒ සියල්ලම විචලනය වන්නේ සන්තතිකව වීමයි.

ඒ අනුව ඩිජිටල් යනු යම් කෘත්‍රිම තත්වයක් බව පෙනෙනවා. එය මිනිසාගේ නිර්මාණයකි. ඩිජිටල් සංඥාවක අවස්ථා ගණන නිශ්චිතයිනෙ. තවද, හැමවිටම වාගේ අප භාවිතා කරන්නේ අවස්ථා 2ක් පමණක් ඇති අවස්ථාවයි. ඩිජිටල් සංඥාවක් නිරූපණය කිරීමට හැකි සරලතම ආකාරය මෙයයි (එහෙත් අවස්ථා 4 හෝ 8 හෝ 16 වැනි යොදා ගන්නා තැන්ද තිබෙනවා). මෙම අවස්ථා දෙක වෙන් කොට හඳුනා ගැනීමට නම්/සලකුනු දෙකක් යොදා ගන්නවා. එක් අවස්ථාවක් True (T), High (Hi), Yes (Y), On හෝ 1 ලෙස හඳුන්වන අතර, අනෙක් අවස්ථාව False (F), Low (Lo), No (N), OFF හෝ 0 ලෙස හඳුන්වනවා. අප මෙම පාඩම් මාලාව සඳහා 1, 0 යන නිරූපණ ක්‍රමය යොදා ගමු. එවිට 1 මඟින් ඩිජිටල් සංඥා 1ද, 0 මඟින් ඩිජිටල් සංඥා 0ද හැඟවේ.

සංඥාවක් නිරූපණය සඳහා යොදා ගත හැකි ඕනෑම ගතිගුණයක් මඟින් ඩිජිටල් සංඥාවක් නිරූපණය කළ හැකියි. උදාහරණයක් ලෙස, අත්පුඩියක් සැරෙන් ගැසීම ඩිජිටල් සංඥා 1 ලෙසත්, අත්පුඩිය සැර අඩුවෙන් ගැසීම ඩිජිටල් සංඥා 0 ලෙසත් සැලකිය හැකියි. බලන්න ඩිජිටල් සංඥා නිරූපණය කිරීම කොතරම් පහසුද කියා. තවත් උදාහරණයක් ලෙස, යම් ශබ්දයක්/නාදයක් තත්පර 3ක කාලයක් පුරා නාද කිරීම 1 ලෙසද, එම ශබ්දයම තත්පර 1ක කාලයක් පුරා නාද කිරීම 0 ලෙසද ගත හැකියි. ඔබට මතක නම්, මෝර්ස් කෝඩ් ක්‍රමය සාදා තිබුණේ මෙවැනි ක්‍රමයක් මත නේද? ඒ කියන්නේ මෝර්ස් කෝඩ්ද ඩිජිටල් සංඥා ක්‍රමයකි. කැමති නම් ආලෝකයෙන්ද ඩිජිටල් සංඥා නිරූපණය කළ හැකියි (කිහිප ආකාරයකින්ම). ටෝච් එකක් (හෝ එල්ඊඩී හෝ ලේසර් එකක්) ගෙන එය තත්පර 2ක කාලයක් දල්වා සිටීමෙන් 1ද, තත්පරයක කාලයක් දල්වා සිටීමෙන් 0ද නිරූපණය කළ හැකියි. එහෙමත් නැතිනම්, වර්ණ දෙකක් පිට කළ හැකි බල්බයක් ගෙන එක් වර්ණයක් යම් කාලයක් පුරාවට දල්වා සිටීමෙන් 1ද, අනෙක් වර්ණය එවැනිම කාලයක් දල්වා සිටීමෙන් 0ද නිරූපණය කළ හැකියි. එහෙමත් නැතිනම්, ටෝච් එලිය ඩිම් කර (ආලොකය අඩු කර) යම් කාලයක් පුරා දල්වා සිටීම 0 ලෙසද, එලිය උපරිම කර එම කාලය තුල දල්වා සිටීම 1 ලෙසත් සැලකිය හැකියි. ඩිජිටල් සංඥා යැවීමට ඔබේ අතේ ඇඟිලිවලින්, ඔබේ ඇස්වලින්, වෙනත් අංගචලනයකින් ආදී ලෙස සිය ගණනක් වූ ක්‍රම ඔබට දැන් සිතා ගත හැකි විය යුතුයි.

එහෙත් ඉලෙක්ට්‍රොනික්ස්, පරිගනක හා සන්නිවේදන තාක්ෂණය තුල ඩිජිටල් සංඥා නිරූපණයට යොදා ගන්නේ විදුලිය හා ලේසර් ආලෝකයයි. විදුලිය ගලා යන කම්බියක්/වයරයක් සලකන්න. එම වයරය තුලින් ගලා යන විදුලියේ වෝල්ටියතාව හැමවිටම නිශ්චිත විය හැකියි. එවිට එම වයරය හරහා යන විදුලි සංඥාව ඩිජිටල් යැයි කියනවා. හැමවිටම වාගේ වයරයක් දිගේ ඩිජිටල් විදුලි සංඥා ගලා යන්නේ වෝල්ට් 5 හෝ වෝල්ට් 0 වශයෙනි (එනම් නිශ්චිත වෝල්ට් අගයන් දෙකකි). පහත රූපයේ දැක්වෙනවා වයරයක් දිගේ ඩිජිටල් විදුලි සංඥාවක් ගලා යන හා ඇනලොග් විදුලි සංඥාවක් ගලා යන අවස්ථා දෙකම.

ඩිජිටල් සංඥාවක් මෙලෙස කොටු හැඩයකින් පෙනෙනවා හැමවිටම. ඩිජිටල් සංඥාවක් ගෙන බැලීමෙන් තවත් වැදගත් ලක්ෂණ කිහිපයක් අපට දැනගත හැකියි. ඩිජිටල් 0 හා ඩිජිටල් 1 යන අවස්ථා දෙකම යම් වෝල්ටියතා අගයන් දෙකකින්නෙ (වෝල්ට් 0 හා වෝල්ට් 5) නිරූපණය කළේ. වෝල්ට් 0 වේවා වෝල්ට් 5 වේවා, යම් කුඩා කාලයක් පුරා ඒ අදාල වෝල්ටියතාව පවත්වාගෙන යා යුතුයි. සිතමු එම කාලය මිලිතත්පරයක් කියා. එවිට, එක් තත්පරයක කාලයක් තුල 1 හෝ 0 ලෙස ඩිජිටල් සංඥා 1000ක් යැවිය හැකියි නේද? ඒ කියන්නේ එම වයරය හරහා තත්පරයට “ඩිජිටල් සංඥා” 1000 ක වේගයෙන් සන්නිවේදනය සිදු වේවි. සංඥාව පවතින කාලය අඩු කිරීමෙන් මෙම වේගය තවත් වැඩි කර ගත හැකියි. මයික්‍රොතත්පරයක් දක්වා සංඥා කාලය අඩු කළොත්, තත්පරයට “ඩිජිටල් සංඥා” මිලියනයක් යැවිය හැකි වේවි. තත්පරයට ඩිජිටල් සංඥා යවන වේගයට අප එහි සම්ප්‍රේෂන වේගය කියා කියනවා. තවද, “ඩිජිටල් සංඥාව” යන වචනය වෙනුවට බිට් (bit) යන වචනය යොදනවා. Bit යන්න සෑදී තිබෙන්නේ binary+digit යන වචන දෙක කෙටි කිරීමෙනි. ඒ කියන්නේ සම්ප්‍රේෂන වේගය තත්පරයට බිට් (bits per second – bps) යන ඒකකයෙන් තමයි හැඳින්වෙන්නේ.

මේ අනුව, බිට් එකක් යනු ඩිජිටල් සංඥාවක කුඩාතම අගයයි. බිට් එකක් එක්කෝ 0 වේ; නැතහොත් 1 වේ. ඒ කියන්නේ එක් බිට් එකකින් හැකියි සංඥා දෙකක් නිරූපණය කරන්නට (0 හා 1). එක ළඟ බිට් 2ක් තැබූ විට සංඥා 4ක් ඒ අනුව සෑදිය හැකියි - 00, 01, 10, 11. එක ළඟ බිට් 3ක් තැබීමෙන් එකිනෙකට වෙනස් සංඥා 8ක් සෑදිය හැකියි - 000, 001, 010, 011, 100, 101, 110, 111. බිට් 4ක් එලෙස ගත් විට, සංඥා 16ක්ද, බිට් 5ක් ගත් විට සංඥා 32ක්ද ආදී ලෙස නිරූපණය කළ හැකියි. ඕනෑම බිට් ගණනක් (N) ගත් විට, ඉන් නිරූපණය කළ හැකි සංඥා ගණන 2^N යන සරල සූත්‍රයෙන් සෑදිය හැකියි. ඒ කියන්නේ බිට් 1ක් විට (එනම්, N=1), 2¹ = 2 නිසා, ඉන් කියන්නේ බිට් 1කින් සංඥා 2ක් නිරූපණය කළ හැකි බවයි. බිට් 4ක් විට (N⁴ = 16), ඉන් සංඥා 16ක් දැක්විය හැකියි. බිට් 8ක් ගත් විට, 2⁸ = 256 නිසා, බිට් 8කින් එකිනෙකට වෙනස් සංඥා 256ක් දැක්විය හැකියි. බිට් 8ක් එලෙස එකට ගත් විට, ඊට බයිට් (byte) එකක් යැයි කියනවා. බිට් යන වචනය සේම බයිට් යන වචනයත් නිතරම පරිගනක හා ඩිජිටල් තාක්ෂණයේදී භාවිතා කෙරෙනවා. සමහර වෙලාවට ඩිජිටල් දත්ත සම්ප්‍රේෂනය වන වේගය තත්පරයට බිට් (bps) යන ඒකකය වෙනුවට තත්පරයට බයිට් (bytes per second – Bps) යන ඒකකයෙන්ද දක්වනවා. මෙහිදී කැපිටල් B අකුර යොදන බව මතක තබා ගන්න. 800 bps යන්න තත්පරයට බයිට් යන ඒකකයෙන් දක්වන විට එම අගය 8න් බෙදා 100 Bps ලෙස ලිවිය යුතුය. මේ වෙනස හොඳින් මතක තබා ගන්න; නැතහොත් ඔබේ ගණනය කිරීම් වරදීවි.

මේ ලොව තුල බොහෝ භෞතික ගති ගුණ තිබෙනවා (උෂ්ණත්වය, ශබ්ද, ආලෝකය, පීඩනය, ...). මේ සෑම ගති ගුණයක්ම පාහේ ඇනලොග් බව අප දැන් දන්නවා. තවද, මේ බොහෝ (හෝ සෑම) ගතිගුණයක්ම සුදුසු විද්‍යුත් උපක්‍රමයකින් ඇනලොග් විදුලි සංඥාවක් බවටද පත් කර ගත හැකියි (මෙම විද්‍යුත් උපක්‍රම/උපාංග tranducer යනුවෙන් හඳුන්වන බවද අප ඉගෙන ගත්තා). උදාහරණයක් ලෙස, මයික් එක යනු ශබ්දය යන භෞතික ගුණය ඊට අනුරූප විදුලි සංඥාවක් බවට පත් කරපු tranducer එකයි). මෙලෙස ලබා ගත් ඇනලොග් විදුලි සංඥා සමග ඍජුවම අපට කටයුතු කළ හැකියි. ඒ සඳහා වර්ධක (amplifier), පෙරන (filter) ආදී ලෙස නොයෙක් ඇනලොග් ඉලෙක්ට්‍රොනික් පරිපථ (analog circuits) සාදා ගත හැකියි කැපෑසිටර්, රෙසිස්ටර්, ඉන්ඩක්ටර්, ඩයෝඩ, ට්‍රාන්සිස්ටර් වැනි ඇනලොග් ඉලෙක්ට්‍රොනික් උපාංග යොදා ගනිමින්.

ඉතිං, ඩිජිටල් සංඥාවල ඇනලොග් සංඥාවලට නැති යම් යම් ඉතා වටිනා ගතිගුණ තිබෙන බැවින්, අපට හැකියි ඉහත ඇනලොග් විදුලි සංඥා ඩිජිටල් විදුලි සංඥා බවට පත් කරගෙන මෙම වාසි අත්පත් කර ගන්න. ඇනලොග් විදුලි සංඥාවක් ඉතා පහසුවෙන්ම ඩිජිටල් සංඥාවක් බවට පත් කර ගත හැකියි Analog-to-Digital Converter (ADC) නමින් හැඳින්වෙන පරිපථයකින්. දැන් මෙම ADC පරිපථ කුඩා IC එකක් වශයෙන් කුඩා මුදලක මිලදී ගත හැකියි.

මෙම ADC පරිපථයට/අයිසී එකට ඇතුලු කරන ඇනලොග් සංඥාව ඩිජිටල් සංඥාවක් ලෙස පිට වේ. දැන් අප සතුව තිබෙන්නේ භාහිර පරිසරයක පවතින යම් භෞතික ගතිගුණයකට අදාල ඩිජිටල් විදුලි සංඥාවකි. අපට හැකියි මෙම ඩිජිටල් සංඥාවත් සුදුසු ඩිජිටල් පරිපථ (digital circuits) මඟින් විවිධ වැදගත් වෙනස් කිරීම් හෙවත් සැකසීම් (processing) සිදු කරන්න.

අපට අවශ්‍ය සැකසීම් සිදු කළ පසු, බොහෝවිට ඩිජිටල් සංඥාව නැවත ඇනලොග් සංඥාවක් බවට පත් කර ගැනීමට සිදු වෙනවා. උදාහරණයක් ලෙස, මයික් එකකින් ලබා ගත් ඇනලොග් සංඥාව ඩිජිටල් කර, පසුව ඊට සුදුසු සැකසීම් සිදු කර, එය නැවත ශබ්ද තරංගයක් ලෙස ස්පීකරයකට යොමු කිරීමට අවශ්‍ය වෙනවානෙ. ඉතිං ස්පීකරයකට ඩිජිටල් සංඥා යැවුවොත් නීක් නීක් වැනි ශබ්දයක් පමණක් ඇසේවි. ඩිජිටල් සංඥාවක් ඇනලොග් කරන්නේ Digital-to-Analog Converter (DAC) නම් පරිපථයකිනි. එයද සුලු මුදලකට අයිසී එකක් වශයෙන් මිලදී ගත හැකියි.

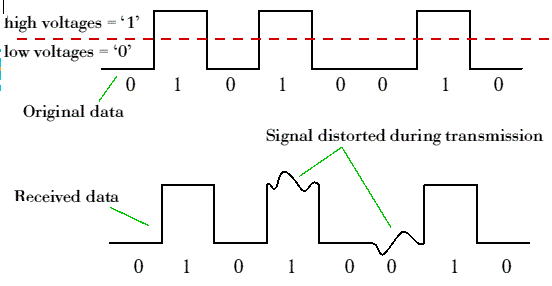
ඒ අනුව පෙනෙනවා, ඩිජිටල් සංඥා අපට අවශ්‍ය කරන්නේ සැකසීම් සඳහා බව. එනම් ඩිජිටල් තාක්ෂනය අතරමැද අවශ්‍යතාවක් ඉටු කර දෙන්නකි. ඇනලොග් සංඥා වෙනුවට ඩිජිටල් සංඥා සැකසීම් සඳහා යොදා ගන්නේ එහි වැදගත්කමක් තිබෙන නිසා විය යුතුයිනෙ. දැන් බලමු ඩිජිටල් සංඥාවල තිබෙන මෙම සුවිශේෂිතා මොනවාද කියා.

1. ඩිජිටල් සංඥාවක් සම්ප්‍රේෂනය කරන විට, එම සංඥාව දුර්වල වුවත්, කිසිදු අඩුපාඩුවක් නැතිව එම ඩිජිටල් සංඥාව නැවත තිබුණු මට්ටමටම පත් කළ හැකියි (immunity from interference). මීට හේතුව ඩිජිටල් සංඥාව මට්ටම් 2ක් පමණක් යොදා ගැනීමයි. සිතන්න එම ඩිජිටල් සංඥාව සම්ප්‍රේෂනය වන කාලය තුල විවිධ බාධාවලට ලක් වී සංඥා හැඩය යම් විකෘතියකට ලක් වූවා කියා (පහත රූපය බලන්න). එසේ විකෘති වුවත්, එම විකෘති වෙච්ච සංඥාව නැවත පහසුවෙන් ප්‍රකෘති කළ හැකියි මොකද විකෘතිය තිබියදීත් යම් කොටු ස්වභාවය එහි තවමත් තිබෙනවා.

ඇනලොග් සංඥාවට එම හැකියාව නැත. සිතන්න යම් ඇනලොග් සංඥාවක් සම්ප්‍රේෂනය වන විට, ඊට ඇති වන විවිධ බාධක නිසා එම සංඥාව යම් විකෘතියකට ලක් වූවා කියා. දැන් විකෘති වෙච්ච සංඥාවේ විකෘති වෙච්ච කොටස කොහොමද ප්‍රතිග්‍රහක පරිපථය විසින් හඳුනා ගන්නේ. එම ග්‍රාහක පරිපථයට විකෘති වෙච්ච කොටසත් දැනෙන්නේ සාමාන්‍ය සංඥාවේ කොටසක් ලෙසමයි (මොකද ඇනලොග් සංඥාවට ඕනෑම අක්‍රමවත් හැඩයක් ගත හැකි නිසා).

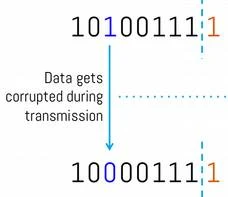
එහෙත් සමහර අවස්ථා තිබෙනවා ඩිජිටල් සංඥාව වුවද එහි කොටු හැඩය මැකී යන ලෙසම විකෘති විය හැකියි. මෙවන් අවස්ථාවලදී ඩිජිටල් සංඥාව නැවත ප්‍රකෘති කළ නොහැකි වේවි. මෙවන් අවස්ථා සඳහා ඩිජිටල් සංඥාව පහත දැක්වෙන අනෙක් සුවිශේෂි ලක්ෂණයෙන් ප්‍රයෝජන ලබනවා.

2. සාමාන්‍යයෙන් ඩිජිටල් සංඥාවක් විකෘති වූ විට වෙනත් උපක්‍රමයක් නැතිවම ප්‍රකෘති කළ හැකි වුවත්, කලාතුරකින් එම හැකියාව නැති වන තරමටම විකෘති විය හැකි බව ඉහතදී පැවසුවා. එවන් අවස්ථා සඳහා මුහුණ දීමට සම්ප්‍රේෂනයට (ප්‍රකෘති කළ නොහැකි) විකෘතියක් ඇති වූ බව දැන ගැනීමට මෙන්ම, ඉන්පසු ඊට කුමක් කළ යුතුදැයි එම සංඥාවට “ඉගැන්විය” හැකියි. වරද හඳුනා ගැනීම (error detection) හා වරද නිවැරදි කිරීම (error correction) ලෙස මෙය හැඳින්විය හැකියි. මෙය සිදු කරන ක්‍රම ගණනාවක්ම ඇති අතර, ඉන් ක්‍රම දෙකක් පමණක් දැන් සලකා බලමු.

උදාහරණයක් ලෙස පහත දැක්වෙන කුඩා ඩිජිටල් සංඥාව සම්ප්‍රේෂනය කිරීමට අවශ්‍ය යැයි සිතමු. මෙම බිට්වල යම් සංඥාවක් හෙවත් දත්තයක් (data/information) ගැප්ව පවතින තිබෙන නිසා, මේවා data bits (දත්ත බිට්) ලෙස හැඳින්විය හැකියි.

1001010 0110011 1011100 0011111 1111111 1010101 1001101

දැන් ඉහත සංඥාවට ඉගැන්විය යුතුයි ප්‍රකෘතිමත් කළ නොහැකි තරමේ විකෘතියක් ඇති වුවොත් එය හඳුනා ගන්නා විදිය. ඒ සඳහා අපට මෙවැනි සරල උපක්‍රමයක් යෙදිය හැකියි. සෑම ඩේටා බිට් 7කට (හෝ 8ක් හෝ) පසුව වැරදි හඳුනාගැනීමේ බිට් එකක් යොදනවා. මෙම විශේෂ බිට් එක parity bit ලෙස නම් කෙරෙනවා. යම් බිට් එකක 0 හෝ 1 යන අගයන් දෙකෙන් එකක්නෙ තිබිය හැක්කේ. එලෙස තිබිය හැකි අගය තීරණය කරන්නේ මෙලෙසය. පැරිටි බිට් එකට පෙර ඇති ඊට අදාල ඩේටා බිට් 7 හි තිබෙන 1 යන සංඥා ගණන ඉරට්ටේ ගණනක් නම්, පැරිටි බිට් අගය 0 වේ. අර බිට් 7 හි තිබෙන 1 යන සංඥා ගණන ඔත්තේ ගණනක් නම්, පැරටි බිට් අගය 1 වේ. උදාහරණයක් ලෙස, ඉහත සංඥාවේ පළමු බිට් 7 බලන්න. එහි 1 සංඥා 3ක් තිබේ. එය ඔත්තේ ගණනක් නිසා, පැරිටි බිට් අගය 1 විය යුතුය. එලෙසම ඉහත සංඥාවෙහි දෙවැනි බිට් 7 බලන්න. එහි 1 සංඥා 4ක් තිබෙන නිසා, පැරිටි බිට් එක 0 වේ. පැරිටි බිට්ද එක් කළ පසු ඉහත සංඥාව පහත ආකාරයට විය යුතුය (පැරිටි බිට් යටින් ඉරි ගසා තිබෙන්නේ පහසුවෙන් පෙනීම සඳහා පමණි).

10010101 01100110 10111000 00111111 11111111 10101010 10011010

දත්ත බිට් (data bits) 7ත් පැරිටි බිට් 1ත් එකට ගෙන එය එක ඒකකයක් ලෙස සලකනවා. ඉහත විදියට පැරිටි බිට් සැකසීමේදී නිවැරදි (ඒ කියන්නේ විකෘතියක් සිදු නොවූ) දත්ත ඒකකයකදී 1 සංඥා හැමවිටම ඉරට්ටේ සංඛ්‍යාවක් තිබිය යුතුයි. දත්ත බිට්වල දැනටමත් 1 යන්න ඉරට්ටේ ගණනක් තිබෙන විට, පැරිටි බිට් එක 0 නිසා, බිට් 8ක් සහිත සම්පූර්ණ දත්ත ඒකකයේද 1 සංඥා ඉරට්ටේ ගණනක් පවතිනවා. දත්ත බිට්වල 1 සංඥාව තිබෙන්නේ ඔත්තේ ගණනක් නම්, පැරිටි බිට් එක 1 බවට පත් කර බිට් 8කින් සමන්විත දත්ත ඒකකයේ 1 යන සංඥා ගණන ඉරට්ටේ බවට පත් වෙනවා. මෙනිසා මෙම පැරිටි ක්‍රමය even parity (ඉරට්ටේ පැරිටි) ලෙස හැඳින්වෙනවා. මෙලෙසම අපට හැකියි odd parity (ඔත්තේ පැරිටි) ක්‍රමයක් සකසන්නත්. මෙවිට, දත්ත බිට්වල 1 යන්න ඔත්තේ ගණනක් ඇති විට, පැරිටි බිට් එක 0 ලෙසද, දත්ත බිට්වල 1 යන්න ඉරට්ටේ ගණනක් ඇති විට, පැරටි බිට් එක 1 ලෙසද තැබිය යුතුයි.

ඔඩ් වේවා ඊවන් වේවා පැරිටි බිට් එකකින් කොහොමද විකෘතියක් හඳුනා ගන්නේ? හරිම පහසුය. අපි ඊවන් පැරිටි ක්‍රමය උදාහරණයට ගමු. මෙහිදී විකෘතියක් නොවූ දත්ත ඒකකය තුල 1 සංඥාව ඉරට්ටේ ගණනක් තිබිය යුතුය. එහෙත් යම් විකෘතියක් නිසා එම දත්ත ඒකකය තුල තිබෙන යම් ඩිජිටල් සංඥාවක් විකෘති වී 1 යන්න 0 බවට හෝ 0 යන්න 1 බවට විකෘති වුවොත්, දැන් එම දත්ත ඒකකයේ පවතින්නේ 1 සංඥාව ඉරට්ටේ ගණනක් නොව ඔත්තේ ගණනකි. එවිට පරිපථයට පහසුවෙන්ම වැටහෙනවා එම දත්ත කොටස යම් විකෘතියකට ලක්ව ඇති බව. පහත රූපයේ එක 1 සංඥාවක් යන්න 0 යන සංඥාව බවට පත්ව ඇත. එවිට දැන් එහි දත්ත බිට් ඉරට්ටේ ගණනක් ලෙස සකස් වේ. එහෙත් මෙය ඊවන් පැරිටි ක්‍රමය යොදා ගන්නා බැවින්, දත්තයේ අග තිබිය යත්තේ 0 නේද? එහෙත් එහි තිබෙන්නේ 1 වේ. ඉන් ග්‍රාහකය වටහා ගන්නවා අතරමැද යම් බිට් එකක් වෙනස් වී ඇති බව.

මෙම ක්‍රමය ඉතාම සරල වන අතර, එය පරිගනකවල බහුලවම යොදා ගැනේ (සාමාන්‍යයෙන් පරිගනකයක් තුල විකෘතිතා ඇතිවීම සාපේක්ෂව ඉතා අඩුය). දත්ත බිට්වලට අමතරව දැන් පැරිටි බිට්ද තිබේ. සෑම දත්ත බිට් 7ක් සඳහාම පැරිටි බිට් එකක් බැගින් වැඩි වන අතර, එය ප්‍රතිශතයක් ලෙස (1/7)x100% = 14% ක වැඩි වීමකි. එබැවින් එය එක්තරා විදියක අකාර්යක්ෂමතාවක් ලෙසද සැලකිය හැකියි. එහෙත් එම වැඩිපුර යොදන බිට්වලින් අපට ඉතා වැදගත් මෙහෙයක් සිදුවන බැවින් (එනම් වැරදි හඳුනාගැනීම) එම අකාර්යක්ෂමතාව නොසලකා හැරිය හැකිය.

මෙම දත්ත ඒකකයේ සංඥා දෙකක් එකවර විකෘති වුවොත් නම් ඉහත පැරිටි ක්‍රමයෙන් වැරැද්ද හඳුනාගැනීමට නොහැකි වේවි මොකද එවිට සංඥා දෙකක් විකෘති වීමෙන් ඉරට්ටේ ගුණය නැවත ලැබෙන නිසාය. එවන් අවස්ථා පරිගනකයක් හෝ යම් ඩිජිටල් උපකරණයක් ඇතුලේ ඇති වීම අඩු වුවත්, විශාල දුරක් ඔස්සේ ඩිජිටල් දත්ත සම්ප්‍රේෂනය වන විට එය පහසුවෙන් සිදුවිය හැකියි. එවැනි අවස්ථාවලටද මුහුන දිය හැකි ක්‍රමත් තිබෙනවා.

CRC (Cyclic Redundancy Check) යනු එවැනි ක්‍රමයකි. මෙහිදී දත්ත බිට් සියල්ල බිට් 64ක්, 256ක් හෝ ඊටත් වැඩි ගණනක් වන පරිදි දත්ත බිට් කාණ්ඩවලට (block) බෙදනවා. එහෙමත් නැතිනම් සංඥාවට අදාළ සම්පූර්ණ බිට් ටිකම එක බ්ලොක් එකක් ලෙස සැලකියද හැකිය. ඊට පසුව ඒ සෑම බ්ලොක් එකකට පසුව CRC යන නමින් හැඳින්වෙන බිට් 4ක් හෝ 8ක් හෝ 16ක් හෝ 32ක් හෝ සමහරවිට ඊටත් වැඩි බිට් ගණනකින් යුතු ඩේටා බිට් බ්ලොක් එකෙහි වැරදි සොයන කොටසක් ඇතුලු කරනවා. මෙම සීආර්සී බිට් කොටසේ අගය සොයන්නේද ඉහත පැරිටි බිට් එකෙහි අගය සොයපු ක්‍රමයට සමාන ක්‍රමයකින්ය. එහෙත් මෙහිදී සරලව ඔත්තේ හෝ ඉරට්ටේ බව සෙවීම නොව, ඊට වඩා තරමක් සංකීර්ණ ගණිතකර්මයක් සිදු කරනවා (ඒ කියන්නේ මේ ක්‍රමය පැරිටි ක්‍රමය තරම් සරල නොවන බවයි). මෙම ගණිත කර්මය සකසා තිබෙන්නේ එම දත්ත බිට් බ්ලොක් එකෙහි එක බිට් එකක අගයක් හෝ විකෘති වුවොත්, මෙම සීආර්සී අගය වෙනස් වන පරිදිය. තවද, මෙහිදී දත්ත බිට් කොතරම් ගණනක් විකෘති වුවද ප්‍රශ්නයක් නැහැ. බිට් සියල්ලම විකෘති වුවත්, සීආර්සි ක්‍රමය සාර්ථකව විකෘති වී ඇති බව දක්වාවි. සමහර අවස්ථාවල checksum, FCS (Frame Check Sequence) වැනි නම්වලින්ද මෙම ක්‍රමය හැඳින්විය හැකියි.

දැන් සිතන්න යම් උපකරණයකින් සීආර්සී ක්‍රමය උපයෝගි කරගෙන ඩිජිටල් ආකාරයෙන් සංඥා සම්ප්‍රේෂනය කරනවා කියා. මෙහිදී එම උපකරණයෙන් ඉහත ආකාරයට දත්ත සියල්ලම බ්ලොක්වලට කඩා, ඒ සෑම බ්ලොක් එකකම ඇති දත්ත බිට් පදනම් කරගෙන යම් ගණනය කිරීමක් සිදු කර ඊට ගැලපෙන සීආර්සී එක සාදා ඒ බ්ලොක් එකට පසුව එම සීආර්සී එක ඈඳනවා. මෙලෙස සෑම බ්ලොක් එකක් පසුපසම ඒ ඒ බ්ලොක් එකට පමණක් ගැලපෙන සීආර්සී තිබෙනවා. දැන් මේ සියලු දත්ත සම්ප්‍රේෂනය වන අතර තුර සිතන්න යම් බ්ලොක් එකක විකෘතියක් ඇති වෙනවා කියා. එම විකෘතිය බිට් 1කට හෝ ඕනෑම ගණනකට විය හැකියි. දැන් මෙම සංඥාව ග්‍රහණය කරපු උපකරණයත් ඒ සෑම ඩේටා බ්ලොක් එකක්ම එකින් එක ගෙන, නැවත සීආර්සී අගයන් ගණනය කරනවා. මෙම නව සීආර්සී අගයන් සම්ප්‍රේෂනය කළ ඩේටා සමග ඇති සීආර්සී අගයන්ට 100%ක්ම සමාන විය යුතුයි. එහෙත් අර විකෘතිය නිසා, නව සීආර්සී අගය ලෙස ලැබෙන්නේ වෙනත් අගයකි (මොකද පෙර සඳහන් කළ ලෙසම, දත්ත බ්ලොක් එකෙහි එක් බිට් එකක හෝ විකෘතියකදී මෙම සීආර්සී අගය වෙනස් වනවා). එය මුල් සීආර්සී අගයත් සමග සසඳන විට වෙනස දැනෙනවා. එවිට ග්‍රාහක උපකරණය හඳුනාගන්නවා මෙම දත්ත බ්ලොක් එක තුල විකෘතියක් පවතින බව.

ඉහත ආකාරයට විකෘති නම් පහසුවෙන් හඳුනාගත හැකියි. එය හඳුනාගත් පසුව කුමක් කළ හැකිද? සමහර ක්‍රම තිබෙනවා එම වරද එලෙස සම්ප්‍රේෂනය වූ දත්තවලින්ම නිවැරදි කරගන්නට හැකියි. එහෙත් එම ක්‍රම තරමක් අකාර්යක්ෂමයි (මොකද දත්ත බිට්වලට අමතරව, යම් විකෘතියක් සිදු වුවොත් එය නිවැරදි කර ගැනීමට අවශ්‍ය වැඩිපුර දත්ත (redundant bits) විශාල සංඛ්‍යාවක්ද යැවීමට සිදුවෙනවා). බොහෝ අවස්ථාවලදී කරන්නේ එක්කෝ එම දත්ත කොටස නොසලකා හැරීම හෝ එම දත්ත කොටස නැවත එවන (retransmit) ලෙස සම්ප්‍රේෂනය කරන උපකරණයට ග්‍රාහක උපකරණය විසින් ස්වයංක්‍රියව දැනුම් දීමයි. අන්තර්ජාලය යනුද ඩිජිටල් දත්ත සම්ප්‍රේෂනය වන පද්ධතියක් වන අතර, ඉහත ක්‍රම සියල්ලම අන්තර්ජාල සේවාවල පවතී (ඒ ගැන සොයා බලන්න).

3. දත්ත හැකිලීමේ (data compression) හැකියාව ඩිජිටල් සංඥාවලට ඇත. දත්ත හකුලනවා යනු, විශාල දත්ත ප්‍රමාණයක් කුඩා බවට පත් කිරීමයි (උදාහරණයක් ලෙස, බිට් ලක්ෂයක දත්ත ගොන්නක් බිට් විසිදහක් තරමට පොඩි කිරීම). දත්ත හැකිලීම දෙයාකාරයකින් පවතිනවා.

එක් ක්‍රමයකදී දත්ත හකුලන විට සමහර දත්ත සදහටම ඉවත් කරනවා. මෙය lossy compression ලෙස හැඳින්වෙනවා. උදාහරණයක් ලෙස, බිට් දසදහක දත්ත ගොඩක් මෙම ලොසි කම්ප්‍රෙෂන් ක්‍රමයට හකුලුවන විට, බිට් තුන්දහසක් අවශ්‍ය නැතැයි ඉවත් කරනවා යැයි සිතන්න. එවිට ඉතිරි වන්නේ බිට් හත්දහකි. එය හැකිලවීමකි. ශබ්ද (audio), වීඩියෝ (video), රූප (graphics/images) නිරූපණය කිරීමට යොදා ගන්නා දත්ත හැමවිටම මෙම ලොසි ක්‍රමයෙන් හැකිලවේ. උදාහරණයක් ලෙස, සාමාන්‍ය සිංදුවක් සඳහා බයිට් මිලියන 40ක් පමණ (එනම් මෙගාබයිට් 40ක්) විශාල දත්ත ප්‍රමාණයක් අවශ්‍ය වෙනවා (හකුලන්නේ නැතිව තිබෙන විට). සීඩී තැටියක සාමාන්‍යයෙන් මෙලෙස හකුලුවන්නේ නැතිවයි සිංදු තැන්පත් කරන්නේ (එනිසා ඔරිජිනල් සීඩී එකක සිංදු 20කට අඩු ප්‍රමාණයක් තිබේවි). එහෙත් මෙම සිංදුවම MP3 නම් ක්‍රමයට හකුලුවන විට, එය බයිට් මිලියන 4කටත් අඩු අගයක් දක්වා කුඩා වේ. බලන්න කොතරම් විශාල හැකිලීමක්ද කියා (ඒකයි mp3 සීඩී එකක සිංදු සිය ගණනක් තැන්පත් කළ හැක්කේ). මෙහිදී ඔරිජිනල් සිංදුවෙහි තිබූ බොහෝ කොටස් ඉවත් වේ. ඒ කියන්නේ සිංදුවේ කොලිටිය අඩු වේ. එහෙත් කොලිටියට එතරම් වෙනසක් සිදු නොවන සේ දත්ත ඉවත් කරන ක්‍රමවේද දැන් අප සතුව ඇත (තාක්ෂණයේ දියුණුව යනු එයයි). wma, wmv, mp3, aac, jpg, gif, mov, mp4 ආදී ලෙස ඔබ පරිගනකවල දකින රූප/ශබ්ද/වීඩියෝ යන දත්තවලට අදාල හැකිලවීමේ ක්‍රම රාශියක් ඇත.

ඔබ අසාවි හැකිලවීමට එලෙස දත්ත ඉවත් කිරීම කරන්නෙ කොහොමද කියා. ඇත්තටම දත්ත සම්ප්‍රේෂන ක්‍රම වෙනමම බරපතල විෂයකි. එහෙත් ඔබට ඇතිවූ මෙම ගැටලුවට සරල පිලිතුරක් දිය හැකියි. සිංදුවක් ගතහොත් එම සිංදුවෙහි තිබිය හැකියි අපේ කනට එතරම් නොඇසෙන ශබ්ද. ඉතාම ඝෝෂාකාරි පරිසරයක් ගැන සිතා බලන්න. එවන් පරිසරයක අසල සිටින කෙනෙකු ඉතා ලස්සන සිංදුවක් මිමිනුවත් ඔබට එය ඇහෙන්නේ නැහැ නේද? අන්න එවැනි ශබ්ද අපට දැන් ඉවත් කර සංඥාවේ දත්ත ප්‍රමාණය අඩු කරගත හැකියි. ඊට අමතරව මිනිස් කන සම්බන්දයෙන් විද්‍යා පර්යේෂන මඟින් සොයා ගත් නව දැනුම (psycho-acoustics) ඉවහල් කරගෙන ඇත (එමඟින් කනට කොලිටියේ වෙනසක් නැතිව යම් යම් දත්ත ඉවත් කිරීමට හැකියාව ලැබේ). තවත් උදාහරණක් සඳහා පහත රූපය බලන්න. මෙහි පසුබිම දළ වශයෙන් නිල්පාටය. සමහරවිට ඔබේ ඇසට මෙය එකම නිල් පාටක් ලෙස පෙනුනත් සැබැවින්ම සංවේදී උපකරණයකට එතැන විවිධ නිල් පැහැයන් පෙනේවි. ඉතිං ඇසට අසංවේදී එක් එක් වර්ණය ගැන නිකරුණේ තිබෙන දත්ත ඉවත් කර එම පසුබිමම තනි නිලක් සේ සැලකිය හැකියි. ශබ්දවල මෙන්ම ඇස සම්බන්ධයෙන්ද විද්‍යාවෙන් සොයාගත් දැනුම මෙහිදීත් යොදා ගන්නවා (ඇසට කොලිටියේ වෙනසක් නොදැනී යම් දත්ත ඉවත් කිරීමට ඉන් හැකියි).

දෙවැනි හැකිලවීමේ ක්‍රමය lossless compression ලෙස හැඳින්වේ. මෙහිදී දත්ත ඉවත් කර දැමීමමක් නැත. මෙම ක්‍රමය හැමවිටම වාගේ යොදා ගන්නේ අක්ෂර (text) නිරූපණය කරන ඩිජිටල් සංඥා සඳහාය. ඔබම සිතා බලන්න යම් ලියුමක් ලොසි ක්‍රමයෙන් හකුලුවන්නට ගියොත් ඉන් කියවෙන්නේ ලියුමේ යම් යම් අක්ෂර ඉවත් කිරීමක්නෙ. එවිට, එම ලියුමේ පනිවුඩය විකෘති වී විශාල අනර්ථයන් පවා සිදු විය හැකියි. එහෙත් එලෙස දත්ත ඉවත් නොකර ටෙක්ස්ට් හැකිලීමට ක්‍රම ගණනාවක්ම තිබෙනවා. මීට අමතරව විවිධ අවශ්‍යතා නිසා රූප/ශබ්ද/වීඩියෝ යන දත්තද ලොස්ලස් ක්‍රමයට හැකලවීමද සිදු කරනවා. එවිට ඔරිජිනල් රූපය/ශබ්දය එලෙසම කිසිදු කොලිටි අඩුවක් නොවී පවතීවි. පහත රූපයේ දැක්වෙන්නේ එකම රූපය ලොස්ලස් හා ලොසි ක්‍රම දෙකෙන්ම හකුලුවා තිබෙන විට පෙනෙන අවස්ථාවකි. බලන්න වෙනස. හකුලුවන විට සියුම් හැඩතල හා වර්ණ මැකී යනවා.

දත්ත හැකිලීම නිසා වැඩි දත්ත ප්‍රමාණයක් කුඩා ඉඩක (සීඩී එකක වැනි) ගබඩා කිරීමට හැකිවෙනවා. තවද, යම් තැනක සිට තවත් තැනකට මෙම දත්ත සම්ප්‍රේෂනය කිරීම ඉන් වේගවත් වෙනවා. එම වාසි නිසා, ඩිජිටල් සංඥා භාවිතා කරන සෑම පද්ධතියක්ම දත්ත හැකිලීම භාවිතා කරනවාමයි. ඩිජිටල් ටීවී, ඩිජිටල් රේඩියෝ, සැටලයිට් දත්ත සම්ප්‍රේෂන, ඩිජිටල් කැමරා, ජංගම දුරකතන, අන්තර්ජාලය යන සියල්ල මේ අතර වේ. හකුලවපු දත්ත නැවත තිබූ තත්වයට පත් කිරීම uncompression හෙවත් decompression ලෙස හැඳින්වේ. ලොස්ලස් ක්‍රමයට හකුලවපු දත්ත නම්, 100%ක්ම තිබූ තත්වයට පත් වුවත්, ලොසි ක්‍රමයට හකුලවපු දත්ත 100%ක්ම තිබූ ඔරිජිනල් තත්වයට පත් නොවේ මොකද හකුලුවන විට සමහර දත්ත සදහටම ඉවත් කරපු නිසා. එසේ වුවත් මුල් තත්වයට ආසන්න තත්වයක පවතීවි (එය තීරණය වන්නේ ඔබ කොපමණ අනුපාතයකින් හැකිලුවාද යන්න මතයි; වැඩිපුර හකුලුවන විට වැඩිපුර දත්ත ඉවත් වී කොලිටිය අඩුවේ).

4. ආරක්ෂක දත්ත කේතීකරණය (data encryption) – සාමාන්‍ය ඩිජිටල් දත්තයක් සම්ප්‍රේෂනය කරන විට, තවත් අතරමැදියෙකුට එම දත්ත හොරෙන් ලබාගෙන (ටැප් කර) එම දත්ත කියවිය හැකියි. එවිට ආරක්ෂිත තොරතුරු හෝ සංවේදී තොරතුරුවලට ඉන් බරපතල තත්වයක් ඇති වේ. ඩිජිටල් සංඥා ඉතාම පහසුවෙන් මේ අනතුරින් ඉවත් කළ හැකියි. මෙවිට අතරමැදියෙකු එම දත්ත ලබා ගත්තත් එහි ඇති ඔරිජිනල් දත්තය ඉන් උකහා ගැනීමට නොහැකි වේවි. මෙලෙස යම් දත්තයක් තවත් (අනවශ්‍ය) අයට තේරුම් ගත නොහැකි පරිදි වෙනස් කිරීම එන්ක්‍රිප්ට් කරනවා (encrypt) යැයි පවසනවා. එන්ක්‍රිප්ට් කරපු ක්‍රමවේදය දන්නා අයට පමණයි එම දත්ත දැන් කියවිය හැක්කේ. මෙවිට, ඒ අය එන්ක්‍රිප්ට් කරපු දත්ත ඩික්‍රිප්ට් කරනවා (decrypt); ඒ කියන්නේ නැවත ඔරිජිනල් දත්තය බවට පත් කර ගන්නවා. එන්ක්‍රිප්ට් කිරීමට පෙර තිබෙන දත්තය plain text ලෙස හැඳින්වෙන අතර, එන්ක්‍රිප්ට් කළාට පසුව ලැබෙන දත්තය cipher text ලෙස හැඳින්වෙනවා.

දැනට වානිජමය වශයෙන් භාවිතා කරන සෑම ඩිජිටල් පද්ධතියක්ම මෙලෙස එන්ක්‍රිප්ෂන් ක්‍රම භාවිතා කරනවා. අන්තර්ජාලය හරහා වානිජ කටයුතු (ecommerce) සිදු කරන්නේ, අන්තර්ජාල බැංකු සේවා (Internet banking) වැනි අන්තර්ජාල ආශ්‍රිත බොහෝ සේවාවන් ආරක්ෂිතව සිදු කර ගන්නේ මෙම ක්‍රමවේදයන්ට පින්සිදු වන්නටය. ඔබ යම් වෙබ් අඩවියක් පරිහරණය කරන විට, එම වෙබ් අඩවියේ නමට (ඩොමේන් නේම්) ඉදිරියෙන් https:// වැනි කොටසක් දකින්නේ නම්, එහි ඇති s අකුරින් කියන්නේ එම වෙබ් අඩවිය සමග ඔබ සිදු කරන සියලු ක්‍රියාකාරකම් එන්ක්‍රිප්ෂන් ක්‍රමවේදයෙන් ආරක්ෂිත (secured) කර ඇති බවයි. එතැන තිබෙන්නේ http:// ලෙස නම් එවැනි ආරක්ෂිත එන්ක්‍රිප්ෂන් ක්‍රමවේද අනුගමනය නොකරන බවත් සිහි තබා ගන්න (එවැනි වෙබ් අඩවිවලට ඔබේ වටිනා හෝ රහස්‍ය තොරතුරු ටයිප් කරන්නත් එපා).

සියලුම ජංගම දුරකතන, චන්ද්‍රිකා දුරකතන සේවාද හැමවිටම වාගේ එන්ක්‍රිප්ෂන් ක්‍රම භාවිතා කරනවා. මේ නිසා තමයි, අප සෙල් ෆෝන් එකකින් කතා කරන විට, එම රේඩියෝ සංඥා විශාල ප්‍රදේශයක් හරහා පැතිර ගියත්, එම ප්‍රදේශයේ සිටින කෙනෙකු එම රේඩියෝ තරංග අල්ලාගෙන ඇහුම්කන් දුන්නත් දුරකතන පණිවුඩය ඔහුට නොතේරෙන්නේ. නිකංම චිරිචිරි වැනි ශබ්දයක් පමණක් ඔහුට ඇසේවි. ඉන් අපේ පෞද්ගලිකත්වයට හානි නොකර දුරකතන සංවාදවල යෙදිය හැකියි.

එසේ වුවත්, ජංගම දුරකතනවල භාවිතාවන මෙම එන්ක්‍රිප්ෂන් ක්‍රම හොරෙන් ඩික්‍රිප්ට් කළ හැකි මිල ඉතා අධික උපකරණ ඇති අතර (ඒවා පරිහරණය කිරීම නීති විරෝධි වේ), සමහර රටවල් ආරක්ෂක හේතු මතද, සමහර රටවල් සිටින පාලකයාට වාසි ප්‍රයෝජන අත්පත් කර ගැනීමටද මෙම උපකරණ රහසිගතව යොදා ගන්නවා. ලංකාවේද මහින්ද රාජපක්ෂගේ කාලයේ විරුද්ධ දේශපාලන මත දරන්නන්ගේ රහස් සෙවීමට මෙවැනි උපකරණ භාවිතා කර තිබෙන බවත් ඔහුව ජනපති කමින් එලවා දැමූ පසු එම උපකරණ දැන් භාවිතා නොකරන බවට නිල වශයෙන්ම ජනමාධ්‍ය හා ආරක්ෂක අමාත්‍යංශ විසින් මහජනයාට දැනුම් දී තිබේ. ඒ නිසා ලංකාවේ එම අවලම් තුච්ඡ වැඩේ සිදු බව හිතලුවක් නොව. රාජපක්ෂ වැනි අවජාතක දේශපාලුවන් රජකරන විට, සමහරවිට තාක්ෂණයේ ආනුභාවයෙන් ලැබෙන වටිනාකම් පවා අහිමි වේ.

5. ඩිජිටල් සංඥා සැකසීම (Digital Signal Processing – DSP) – මෙයත් ඩිජිටල්කරණයෙන් ලැබෙන විශාල ප්‍රයෝජනයකි. ඇත්තටම ඉහතදී කතා කළ එන්ක්‍රිප්ෂන්, කොම්ප්‍රෙෂන් යන ක්‍රියාවලි දෙකත් මේ යටතට ගත හැකියි. ඩිජිටල් සංඥාවලට ඉතා පහසුවෙන් විවිධ වෙනස්කිරීම් සිදු කළ හැකියි. දැනටමත් එන්ක්‍රිප්ෂන් හා කොම්ප්‍රෙෂන් ගැන දන්නවානෙ. ඊට අමතරව, යම් දත්ත ගොඩකින් සමහර දත්ත ඉවත් කිරීම හෝ උකහ ගැනීම (filtering) වැදගත් වේ. විවිධාකාරයේ ෆිල්ටර් යොදාගෙන විවිධාකාරයේ වැඩකටයුතු ඉටු කර ගත හැකියි. ඔබ පරිගණකයකින් රූප සකසා ඇත්නම් (photoshop වැනි සොෆ්ට්වෙයාර් එකකින්) හෝ පරිගණකයකින් ශබ්ද සකසා ඇත්නම් (CoolEdit වැනි සොෆ්ට්වෙයාර් එකකින්) මේ ගැන හොඳ වැටහීමක් ඇති කර ගත හැකියි. මේ අවස්ථා දෙකෙහිදීම රූපයට හෝ ශබ්දයට සිදු කළ සියලු වෙනස්කම් මෙම DSP නිසා සිදු වූවකි. රූපයේ යම් යම් තැන්වල වර්ණ වෙනස් කිරීම, කොටස් අපැහැදිලි කිරීම (blur) හෝ ශබ්දයක හඬ වැඩි කිරීම, සංඛ්‍යාත (එනම් ශබ්ද) ගොන්නකින් එක් සංඛ්‍යාතයක් (ශබ්දයක්) වෙන් කර ගැනීම ආදී දේවල් මින් කර ගත හැකියි. ඇත්තටම ඩීඑස්පී මඟින් “මැජික්” කළ හැකියි. DSP මේවන විට දැවැන්ත විෂයක් බවට පත්ව ඇති අතර, අප මේ සලකා බැලුවේ DSP යනු කුමක්ද කියා හැඳින ගැනීම පමණි. වර්තමානයේ DSP අයිසී ඇති අතර, ඩිජිටල් සංඥාවක් මෙවැනි අයිසී එකක් තුලින් යවා විවිධාකාරයේ සැකසීම් රාශියක්ම එකවර සිදුකර ගත හැකියි.

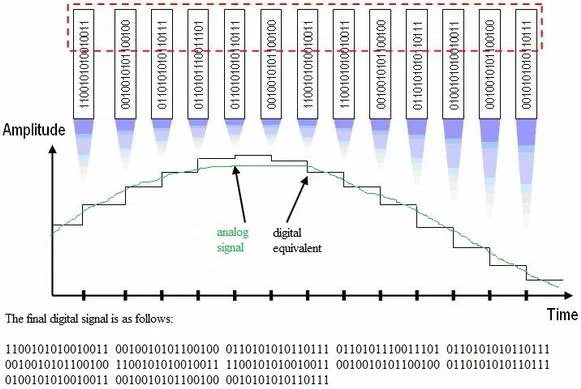
ඩිජිටල් සංඥාවක් සාමාන්‍යයෙන් බිට් මිලියන හෝ බිලියන ගණන්වලින් සමන්විත වේ (ඇත්තටම කුඩා ඇනලොග් සංඥාවක් වුවද ඩිජිටල් බවට පරිවර්තනය කරන විට ඉතා දිගු ඩිජිටල් සංඥා තමයි ලැබෙන්නේ). ඊට හේතුව පෙනේවි ඇනලොග් සංඥාවක් ඩිජිටල් සංඥාවක් බවට පත් කරන්නේ කෙලෙසදැයි දැනගත් විට. පහත රූපයෙන් දැක්වෙන්නේ ඩිජිටල් බවට පත් කර ගත යුතු ඇනලොග් සංඥාවකි. මෙම සංඥාවේ සිරස් අක්ෂයෙන් සංඥා විස්තාරය හෙවත් සංඥාවේ වෝල්ටියතාව නිරූපණය කෙරෙන අතර, තිරස් අක්ෂයෙන් කාලය නිරූපණය වේ (ඔබ දන්නවා සංඥාවක් යනු කාලයත් සමග වෙනස් වන දෙයක් බව).

දැන් අපි කාලය අක්ෂයෙන් එක් නිමේෂයක් (moment) සලකමු. එය පහත රූපයේ ආකාරයට සිරස් රේඛාවක් ඇඳීමෙන් නිරූපණය කළ හැකියි. දැන් එම සිරස් රේඛාව ඇනලොග් සංඥාවේ යම් එක් ස්ථානයක් කපයි. එම ස්ථානයේ වෝල්ටියතාව තමයි එම කාල නිමේෂයේදී සංඥාව සතු අගය/ත්‍රීව්‍රතාව (intensity). පහත රූපයේ අනුව එම අගය වෝල්ට් 2.5කි.

.

දැන් අපිට කරන්නට තිබෙන්නේ එම සම්පූර්ණ ඇනලොග් සංඥාව පුරාම එලෙස සිරස් ඉරි ඇඳීමයි. සිරස් ඉරි අඳිනවා යැයි පැවසුවත් සත්‍ය වශයෙන්ම ඉලෙක්ට්‍රොනික්ස් පැත්තෙන් සිදු වන්නේ එම සංඥාව ගලා යන අතරවාරයේ ඉතා කුඩා කාල පරතර සහිතව (සිතමු මයික්‍රො තත්පරයෙන් මයික්‍රොතත්පරයට කියා) ඒ ඒ අවස්ථාවේදී සංඥාවේ පවතින වෝල්ටියතා අගය කීයදැයි මැනීමයි. මෙම ක්‍රියාදාමය Sampling and Holding හෝ නිකංම sampling ලෙස හැඳින්වෙනවා. මෙය සිදු කරන පරිපථය ඉලෙක්ට්‍රොනික්ස්හිදි Sampling and Holding (S/H) circuit ලෙස හඳුන්වනවා. පහත රූපයේ දැක්වෙන්නේ මෙලෙස සමාන කාල පරතරවලින් ඇනලොග් සංඥාවේ වෝල්ටියතාව මැන ගත් විට ලැබෙන අගයන් සහිත වගුවකි. තත්පරයට කී පාරක් මෙලෙස මනිනවාද යන්න පරිපථය සැලසුම් කරන කෙනා ගන්නා තීරණයකි. තත්පරයක් තුල වැඩිපුර වාර ගණනක් (sampling rate) ගන්නා තරමට හොඳයි; එහෙත් මෙවිට වියදම මෙන්ම ඩිජිටල් සංඥාවේ විශාලත්වයද වැඩි වේ (මෙය මොහොතකින් අවබෝධ වේවි). මෙම සාම්ප්ලිං රේට් එක මනින්නේ හර්ට්ස්වලිනි.

ඇනලොග් සංඥාව ඩිජිටල් කිරීමේ පළමු පියවර එයයි. දැන් දෙවන පියවරට යමු. ඉහතදී එක් එක් නිමේෂයක් සඳහා සොයා ගත් එක් එක් වෝල්ටියතා අගයක් ඇනලොග් අගයක් ලෙසයි පැවතියේ. මෙම එක් එක් ඇනලොග් අගයක් ඩිජිටල් අගයක් (ඒ කියන්නේ දෙකේ පාදයේ අගයක්) බවට පත් කළ යුතුය. මෙම ක්‍රියාවලිය quantization ලෙස හැඳින්වේ. එය සිදු කරන්නේ මෙලෙසයි. පරිපථය සැලසුම කරන කෙනා නැවත තීරණයක් ගන්නවා ඇනලොග් සංඥාවේ ඕනෑම වෝල්ටියතා අගයක් නිරූපණය කිරීමට බිට් කීයක් යොදනවාද යන්න. මේ සඳහා යොදා ගන්නා බිට් ගණන bit depth ලෙස හැඳින්වේ. සිතමු ඔහු බිට් 2ක් යොදා ගන්නවා කියා. එවිට 2² හෙවත් 4ක් වූ එකිනෙකට වෙනස් විවිධ අගයන් ඉන් නිරූපණය කළ හැකියි. උදාහරණයක් ලෙස, ඇනලොග් සංඥාවේ උපරිම අගය වෝල්ට් 4 හා අවම අගය වෝල්ට් -4 නම්, පහත වම් රූපයේ ආකාරයට වෝල්ට් 4ත් -4ත් අතර අගයන් බිට් හතරේ ඩිජිටල් සංඥා අතරේ බෙදා හැරිය හැකියි.

ඒ කියන්නේ මෙම අවස්ථාවේදි එක් ඩිජිටල් කේතයක සිට අනෙක් ඩිජිටල් කේතයට ඇති පරතරය වෝල්ට් 2කි. මෙම පරතරය resolution යන නමින් හැඳින්වේ. රෙසලූෂන් එක ගණනය කරන්නේ උපරිම හා අවම වෝල්ට් ගණන අතර වෝල්ට් පරතරය ඩිජිටල් සංඥා ගණනින් බෙදීමෙනි. එවිට, (4 - (-4) = 8; 8/4 = 2) උදාහරණයක් ලෙස, වෝල්ට් -4 නිරූපණය කරන්නේ 00 යන ඩිජිටල් කේතයෙනි. ඒ විතරක් නොවෙයි, වෝල්ට් -2 දක්වා සියලුම වෝල්ට් අගයන් සඳහාද යොදා ගැනීමට සිදු වන්නේ 00 යන කේතයම තමයි. ඒ අනුව බිට් 2ක් කොහෙත්ම ප්‍රමාණවත් නොවන බව පෙනේ. රෙසලූෂන් අගය අඩුවන තරමට හොඳය. ඉහත රූපයේ බිට් ඩෙප්ත් එක 3 විට තත්වයද පෙන්වා ඇත. බිට් ඩෙප්ත් එක බිට් 8ක් දක්වා වැඩි කළ විට, ඉන් 2⁸ හෙවත් 256ක් දක්වා විවිධ අගයන් නිරූපණය කළ හැකියි. එවිට, බිට් 8කින් සමන්විත එක් ඩිජිටල් කේතයකින් දැන් ලැබෙන රෙසලූෂන් එක 8/256 = 0.03125 වෝල්ට් වේ. ඒ කියන්නේ වෝල්ට් -4 අගය 00000000 යන ඩිජිටල් කේතයෙන් නිරූපණය වන අතර, 00000001 යන ඊළඟ අගයෙන් නිරූපණය වන්නේ -4 + 0.03125 = -3.96875 වේ. ඒ කියන්නේ බිට් 4ක් ගත්තාට වඩා බිට් 8ක් ගත් විට රෙසලූෂන් එක හොඳ මට්ටමකට පත් වී ඇනලොග් සංඥාව ඉතා හොඳ මට්ටමේ ඩිජිටල් සංඥාවක් බවට පත් වේ. බලන්න පහත a රූපයට වඩා වැඩිපුර b රූපයේ සිරස් අක්ෂය බෙදා තිබෙනවා (ඒ කියන්නේ බිට් ඩෙප්ත් එක වැඩියි b වල). මෙවිට ලැබන ඩිජිටල් සංඥාව ඇනලොග් සංඥාවට වඩා සමීප බවක් පෙනෙනවා නේද?

දැන් අවසාන වශයෙන් කරන්නට තිබෙන්නේ ඉහත වගුවේ එක් එක් නිමේෂයක් සඳහා වූ ඇනලොග් අගයන් ඉහත ක්‍රමයට බිට් 8කින් (හෝ වෙනත් බිට් ගණනකින්) යුතු ඩිජිටල් කේත ගොන්නක් බවට පත් කරගත් නිසා, එම සියලු ඩිජිටල් කේතයන් පිලිවෙලට එකක් පිටුපස එකක් සිටින සේ දම්වැලක් සේ සකස් කිරීමයි. මෙවිට ඉතා දිගු ඩිජිටල් තරංගයක් ලැබෙනවා නේද? දැක්කද කුඩා ඇනලොග් සංඥාවක් වුවද ඉතා දිගු ඩිජිටල් සංඥාවක් බවට පත් වෙනවා?

 සාමාන්‍යයෙන් සාම්ප්ලිං රේට් එක තත්පරයට 8000ක් හෝ ඊට වඩා වැඩි අගයක් ගන්නා අතර, බිට් ඩෙප්ත් එක 8ක් හෝ ඊට වැඩි අගයක් වේ. සිංදු තිබෙන සාමාන්‍ය ඕඩියෝ සීඩී එකක සිංදු ඩිජිටල් සංඥා ආකාරයෙන් ගබඩා කර තිබෙන අතර, සම්මතයක් ලෙස එහි සාම්ප්ලිං රේට් එක 44100 හර්ට්ස් වන අතර, බිට් ඩෙප්ත් එක බිට් 16කි. සීඩී සිංදුවක කොලිටිය ඉතා හොඳයි නේද? sampling rate එක වැඩි වන විට සේම, බිට් ඩෙප්ත් එක වැඩි කරන විටත්, ඇනලොග් සංඥාව වඩ වඩා හොඳින් ඩිජිටල් සංඥාවෙන් නිරූපණය කෙරේ. එසේ නම්, කළ යුත්තේ මෙම අගයන් දෙක පුලුවන් තරම් වැඩියෙන් ගැනීම නේද? ඔව්. එසේ වුවත්, එවිට වෙනත් ප්‍රශ්නයක් මතු වේ. එනම්, ඩිජිටල් සංඥාව විශාල වේ. උදාහරණයක් ලෙස, රෙසලූෂන් එක දියුණු කර ගැනීමේ පරමාර්ථයෙන් බිට් ගණන 8 වෙනුවට 16ක් ගත හැකියි. එවිට ඩිජිටල් සංඥාවද දෙගුණයකින් වැඩි වේ. එලෙසම සාම්ප්ලිං රේට් එක දෙගුණයක් කළොත් ඊට සමානුපාතිකව නැවතත් ඩිජිටල් සංඥාව දෙගුණයක් වේවි.

ඉහත විස්තර කළේ Analog-to-Digital පරිපථය/අයිසී එකක් තුල සිදුවන ක්‍රියාවලියයි. එහි ප්‍රතිලෝම ක්‍රියාවලිය සිදු වෙනවා Digital-to-Analog පරිපථය තුල. එනම් ඩිජිටල් තරංගයක් දී ඇති විට, ඊට අනුරූප ඇනලොග් සංඥාව ඉන් නිපදවෙනවා. උදාහරණයක් ලෙස බිට් ඩෙප්ත් එක බිට් 4ක් ලෙස පවතින ඩිජිටල් සංඥාවක් සලකමු. දැන් එම ඩිජිටල් සංඥාව බිට් හතරේ බ්ලොක්වලට කඩනවා (බ්ලොක් එකේ සයිස් එක හැමවිටම බිට් ඩෙප්ත් එකට සමාන වේ). එම එක් එක් බ්ලොක් එකට ගැලපෙන ඇනලොග් වෝල්ටියතාවක් හිමි කර දෙනවා. දැන් මෙලෙස ලැබුණු ඇනලොග් වෝල්ටියතා අගයන් එක පෙලට යවන විට, ඉන් ලැබෙන්නේ ඇනලොග් සංඥාවයි (කාලයට සාපේක්ෂව විචලනය වන වෝල්ටියතාවකි).

බිට් හෝ බයිට් විශාල ගණන් පවතින නිසා, ඒවායේ දහසේ, මිලියනයේ, බිලියනයේ ආදි ගුණාකාරවලින් දක්වන සිරිතක් තියෙනවා. ඒ සඳහා kilo (10³), mega (10⁶), giga (10⁹), tera (10¹²) ආදී ගුණාකාර පදමයි භාවිතා වන්නේ. එහෙත් බිට් හෝ බයිට් සමග මෙම ගුණාකාර පද යොදන විට සාමාන්‍ය අවස්ථාවට වඩා තරමක වෙනසක් තිබෙනවා. ඊට හේතුව බිට්/බයිට් යනු දෙකේ පාදයෙන් ගණන් හදන අගයන් වීමයි. සාමාන්‍ය (ඇනලොග්) තත්වයේදී උදාහරණයක් ලෙස සීනි ග්‍රෑම් 1000ක් සීනි කිලෝග්‍රෑම් 1ක් ලෙස කිව හැකි වුවත්, බිට් 1000ක් කිලෝබයිට් 1ක් නොවේ. ඇත්තෙන්ම බයිට් 1024ක් තමයි එක කිලෝබයිටයක් වන්නේ. එසේ වීමට හේතුව බයිනරි (දෙකේ පාදයේ) පද්ධතියකදී 2¹⁰ = 1024 වේ. කුමන හෝ “දොලදුකක්” නිසා ඒ කාලයේ පරිගණක විද්‍යාඥයන් නිකංම බිට් 1000ක් කිලෝබිට් 1ක් ලෙස සලකනවා වෙනුවට, බිට් 2¹⁰ක ප්‍රමාණය (හෙවත් බිට් 1024ක්) කිලෝබිට් 1ක් ලෙස සලකන්නට පුරුදු වුණා. 1000 හා 1024 අතර ඇත්තේ සුලු වෙනසක් නිසා, එසේ සැලකීම තවත් පහසු වූවා. එනිසා බිට්/බයිට් සම්බන්දයෙන් මෙලෙස 2¹⁰, 2²⁰, 2³⁰ ආදී ලෙසයි ගුණාකාර දක්වන්නේ. ඒ අනුව පහත සම්බන්දතා පහසුවෙන් මතක තබා ගන්න.

බිට් 2¹⁰ = බිට් 1024 (1024 b)= කිලෝබිට් 1 (1 kb)

කිලෝබිට් 2¹⁰ = කිලෝබිට් 1024 = මෙගාබිට් 1 (1 Mb)

මෙගාබිට් 2¹⁰ = මෙගාබිට් 1024 = ගිගාබිට් 1 (1 Gb)

ගිගාබිට් 2¹⁰ = ගිගාබිට් 1024 = ටෙරාබිට් 1 (1 Tb)

මෙලෙසම බයිට් ගැනත් සිතන්න. බයිට් 1024ක් (1024 B) = 1 කිලෝබයිට් (1 kB), කිලෝබයිට් 1024 = 1 මෙගාබයිට් (1 MB), මෙගාබයිට් 1024 = 1 ගිගාබයිට් (1 GB), ගිගාබයිට් 1024 = 1 ටෙරාබයිට් (1 TB) ආදි ලෙස පවතී.

ඇනලොග් සංඥාවක් සුමට වක්‍රයකි. එහෙත් ඩිජිටල් සංඥාවක් කිසිසේත් සුමට නොවේ; එය කොටු සංඥාවකි ඉතිං මෙම කොටු සංඥාවෙන් නැවත ඇනලොග් සංඥාව ඇති කර ගන්නා විට, ඔරිජිනල් ඇනලොග් සංඥාවේ තිබූ සුමට බව එලෙසම නොලැබේ. ඒ වෙනුවට දැන් අපට ලැබෙන්නේ පඩිපෙලක ස්වරූපය හෝ කියත් පටියක දැති ස්වරූපය සහිත (jagged) වක්‍රයකි. මෙය ඇත්තටම ඇනලොග් සංඥාවක් ඩිජිටල් කිරීමේදී අනිවාර්යෙන්ම ඇතිවන අක්‍රමිකතාවකි (විකෘතියකි). බිට් ඩෙප්ත් එක වැඩි කරමින් බොහෝ දුරකට මෙම පඩිපෙල සේ පෙනෙන ගතිය ඉවත් කර වක්‍රය සුමට කළ හැකියි. මෙම විකෘතිය quantization error ලෙස හැඳින්වේ. මෙය සහමුලින්ම ඉවත් කළ නොහැකි වුවත්, පෙර කී ලෙසම බිට් ඩෙප්ත් වැඩි කරමින් යන විට, ක්වන්ටයිසේෂන් එරර් එක ක්‍රමයෙන් අඩු වී අපට වෙනසක් නොදැනෙන මට්ටමක් දක්වා එය අඩු කර ගත හැකියි.

ක්වන්ටයිසේෂන් එරර් එක සුමට ඇනලොග් තරංගය මත ස්ථාපනය වී පවතින එක්තරා විදියක ඝෝෂාවක් (noise) ලෙසත් දැකිය හැකියි. එවිට එම ඝෝෂාව quantization noise ලෙස හැඳින්විය හැකියි. මෙම ඝෝෂාව ඉවත් කළොත් අපට ලැබෙන්නේ අනර්ඝ සුමට ඇනලොග් සංඥාවක් වනු ඇත. ඉහත රූපයේ උඩින් ඇති කොටසින් දැක්වෙන්නේ ඔරිජිනල් සුමට ඇනලොග් සංඥාව (නිල් පාටින්) හා එහි ක්වන්ටයිසේෂන් නොයිස්ද (එනම්, ක්වන්ටයිසේෂන් එරර්) සහිත ඩිජිටල් සංඥාවෙන් නැවත සකස් කරගත් ඇනලොග් සංඥාවයි (රතු පාටින්). මෙම ඝෝෂාව පමණක් අපට වෙනම දැක්විය හැකි අතර පහල කොටසින් දැක්වෙන්නේ එයයි. ඉහත රූපයේ පහත කොටසින් ඒ අනුව දැක්වෙන්නේ ක්වන්ටයිසේෂන් නොයිස් එකේ පෙනුමයි.