සන්නිවේදනය හා ආධුනික ගුවන් විදුලි ශිල්පය (Amateur radio) - 21

විස්තාර මූර්ජනනය

පැරණිතම හා වඩාත්ම පහසුවෙන් තේරුම්ගත හැකි මූර්ජන ක්‍රමය මෙයයි. රේඩියෝ තරංග සොයාගත් කාලයේ මෙම මූර්ජන ක්‍රමය පමණි දැනගෙන සිටියේ. සමහර පැහැදිලි කිරීම් තුල, අනෙක් මූර්ජන ක්‍රමවලට වඩා පහසුවෙන් සිදු කළ හැකි මූර්ජන ක්‍රමය ලෙස මෙය හැඳින්වුවත්, වර්තමානයේ එම ප්‍රකාශය එතරම් නිවැරදි නොවන්නේ, තාක්ෂණයේ දියුනුව නිසා අනෙක් මූර්ජන ක්‍රමද පහසුවෙන් සිදු කළ හැකි තත්වයක අප සිටින නිසාය. විස්තාර මූර්ජනය දෙස පැති කිහිපයකින්ම බැලීම වටිනවා හොඳ අවබෝධයක් ලබා ගැනීමට අවශ්‍ය නම්.

පළමුව බලමු මූර්ජනය නිසා සංඥා සංඛ්‍යාතයට කුමක් සිදු වේද කියා. පැහැදිලි කිරීමේ පහසුව තකා, මුලින්ම සංඥාව සරල අවසංඛ්‍යාත සයිනාකාර තරංගයක් සේ සලකමු. උදාහරණයක් ලෙස, මෙම සයිනාකාර සංඥාවේ සංඛ්‍යාතය හර්ට්ස් 100 යැයි සිතමු. මෙම සංඥා සංඛ්‍යාතය දැන් අධිසංඛ්‍යාත වාහක තරංගය සමග (විස්තාර මූර්ජන ක්‍රමයට) මිශ්‍ර කරමු. මෙම වාහක තරංගය මෙගාහර්ට්ස් 200 යැයි සිතමු. මෙවිට, මූර්ජනය හේතු කොට ගෙන, පහත රූපයේ ආකාරයට මෙගාහර්ට්ස් 200.0001 හෙවත් කිලෝහර්ට්ස් 200,000.1 හෙවත් හර්ට්ස් 200,000,100 මූර්ජිත තරංගයක් ලැබේවි.

එලෙසම සංඥාව හර්ට්ස් 101ක් වූවා නම්, ඉහත ආකාරයටම මෙගාහර්ට්ස් 200ක වාහක තරංගය සමග මිශ්‍ර කළ විට, මෙගාහර්ට්ස් 200.000101 ක හෙවත් හර්ට්ස් 200,000,101 ක මූර්ජිත සංඥාවක් ලැබේවි. ඒ කියන්නේ සංඥා සංඛ්‍යාතය වාහක සංඛ්‍යාතයට එකතු වේ. කිසිම සංඥාවක් නැති විට, මූර්ජිත සංඥාව ලෙස ලැබෙන්නේ මෙගාහර්ට්ස් 200ක වාහක තරංගය පමණි.

එහෙත් අප දන්නවා සංඥාවක සාමාන්‍යයෙන් තිබෙන්නේ විෂම/අක්‍රමවත් හැඩයක් බව. ඒ කියන්නේ ෆූරියර් න්‍යාය අනුව එතැන සයිනාකාර තරංග සෙට් එකක්ම තිබෙනවා. මෙම සයිනාකාර සෙට් එකෙහි එක් එක් සංඛ්‍යාතය දැන් වාහක සංඛ්‍යාතය සමග එකතු කළ යුතු වෙනවා. එවිට අවසානයේ ලැබෙන්නේ සංඥා බෑන්ඩ්විත් එකට සමාන සංඛ්‍යාත පරාසයක් සහිත අධිසංඛ්‍යාත මූර්ජිත සංඥාවක් නේද? එය හරියට අවසංඛ්‍යාත බෑන්ඩ් එක “ඔසවා” අධිසංඛ්‍යාත බෑන්ඩ් එක මත තැබුවා වගෙයි. පහත රූපයේ සංඛ්‍යාත සෙට් එක (පරාසය) අලුපාට පෙට්ටියකින් නිරූපණය කර තිබෙනවා. එහි පෙනෙන පරිදි සංඛ්‍යාත අක්ෂයේ (තිරස් අක්ෂය) පහල අගය පරාසයේ තිබූ පෙට්ටිය මූර්ජනයේදී ඉහල අගය පරාසයට ගෙන ගොස් දමා ඇත. මෙහිදී පෙට්ටියේ සයිස් එක (එනම් සංඥා බෑන්ඩ්විත් එක) වෙනසක් නොවේ. වෙනස් වන්නේ එම බෑන්ඩ්විත් එක සංඛ්‍යාත වර්ණාවලියේ තිබෙන ස්ථානය පමණි.

දැන් බලමු සංඥා හැඩය කෙසේද අධිසංඛ්‍යාත වාහකය මත කාවදන්නේ කියා විස්තාර මූර්ජන ක්‍රමය උපයෝගි කරගෙන. ලෝකල් ඔසිලේටරයෙන් සාමාන්‍යයෙන් පිටවන අධිසංඛ්‍යාත වාහක තරංග පෙල ක්‍රමවත් හැඩයක් මෙන්ම නිශ්චිත උපරිම විස්තාරයක් සහිතය (පහත A රූපය). දැන් එක් එක් වාහක තරංගයේ විස්තාරය ක්ෂණිකව අඩු වැඩි කිරීමට යම් ඉලෙක්ට්‍රෝනික් උපක්‍රමයක් අප සතුව තිබෙනවා යැයි සිතමු. එලෙස වාහක තරංගයේ විස්තාරය විචලනය කළ විට පෙනෙන ආකාරයක් පහත B රූපයේ දැක්වේ (වාහක තරංග පෙලෙහි උඩ හා යට යන මට්ටම් දෙකම එකම විදියට වෙනස් වන බව රූපයේ පෙනේ).

ඉතිං විස්තාර මූර්ජනයේදී අප සිදු කරන්නේ කාලයත් සමඟ විචලනය වන සංඥාවේ විශාලත්වය (වෝල්ටියතා අගය) අනුව වාහක තරංගයේ විස්තාර අගය විචලනය කිරීම තමයි. සංඥාව කාලයත් සමග විචලනය වන නිසා, වාහක තරංගයේ විස්තාරයද ඊට අනුරූප වේගයකින් විචලනය (අඩු වැඩි) වේ. එවිට, සංඥාවේ හැඩය වාහකය මත හෙවත් වාහක විස්තාරය මත ස්ථාපිත වේ. එම සිදුවීම රූපමය ආකාරයෙන් පහත දැක්වේ.

සටහන

පහත රූපයේ වුවමනාවෙන්ම යම් වැරද්දක් මා කර ඇත. සාමාන්‍යයෙන් සංඥාවට අනුව විචලනය වන විට, වාහක තරංගයේ උඩ හා යට මට්ටම් දෙකම එකම විදියට විචලනයක් ඇති කර ගන්නවා ඉහත B රූපයේ පෙන්වා ඇති ලෙසට. එහෙත් මා දැනට පැහැදිලි කිරීමේ පහසුව තකා වාහක තරංගයේ උඩු මට්ටම පමණක් සංඥා හැඩය ලබා ගන්නා හැටි දක්වා තිබෙනවා (එවිට වාහකයේ පහල මට්ටම ස්ථාවරව පවතින ලෙසට ඇඳ තිබෙනවා). ඇත්තටම අපට කර ගැනීමට අවශ්‍යත් එයනෙ. නිකරුනේ මට්ටම් දෙකෙහිම විචලනයක් අපට අවශ්‍ය නැහැනෙ. එසේ වුවත්, තව මොහොතකින් ඔබට පෙනේවි අපට අවශ්‍ය එක පැත්තක් විචලනය වීම වුවත්, ප්‍රායෝගික පරිපථවල හැමවිටම වාහකයේ උඩු හා යටි පැති දෙකෙහිම සංඥා හැඩය ස්ථාපනය වන බව. එසේ වූවා කියා අපට ඇත්තටම අමුතුවෙන් අවාසියක්ද ඇති නොවේ.

දැන් අපි විස්තාර මූර්ජනය ගණිතානුකූලවත් සලකා බලමු. (මාද ඇතුලුව) බොහෝ දෙනා ගණිත සූත්‍ර සමග වැඩ කිරීමට එතරම් කැමැත්තක් නැත. එය ස්වාභාවික තත්වයක් වුවත්, අවශ්‍ය අවස්ථාවලදී ගණිතය යොදා ගැනීම අවශ්‍යයෙන්ම සිදු කළ යුතුය. විද්‍යා හෝ තාක්ෂණික ලෝකයේ සෑම දෙයක්ම ලොකු ලොකු ගණිත සූත්‍ර ආදිය නැතිව නිකංම කතාන්දර වගේ පහසුවෙන් තේරුම්ගත හැකියි (intuitive) යන මුලාවේ අප නොවැටිය යුතුය (එසේ අවබෝධ කර ගත හැකි බොහෝ දේවල්ද තිබේ). ඒ බොහෝ දේවල් අපට සිතින් මවා ගැනීමට බැරිය. ඒවා ගණිත සූත්‍රයන්ට පිංසිදු වන්නට අපට භාවිතා කිරීමට අවස්ථාව ලැබී තිබේ. ඉතිං අවශ්‍ය තැන්වල එවන් ගණිත සූත්‍ර හා ක්‍රමවේද සමඟ හුරුපුරුදු බවක් ඇති කර ගැනීම වැදගත්ය.

අප මීට පෙර තරංග ගැන කතා කරන විට, ඕනෑම තරංගයක්/දෝලනයක්/කම්පනයක් Asin(θ) යන සූත්‍රයෙන් දැක්විය හැකි බව පෙන්වා දුන්නා. මෙහි A යනු තරංග විස්තාරය වන අතර, θ යනු කෝණයයි. කෝණය, කාලය (t) හා කෝණික ප්‍රවේගය (ω) අතර ω = θ/t යන සම්බන්දතාව පවතින නිසා ඉහත සූත්‍රයම Asin(ωt) ලෙසද ලිවිය හැකියිනෙ. තවද, ω = 2πf ලෙස කෝණික ප්‍රවේගය හා සංඛ්‍යාතය (f) අතර සම්බන්දතාවක් පවතින නිසා, ඉහත සූත්‍රයම නැවත Asin(2πft) ලෙස ලිවිය හැකියි.

v = Asin(θ) = Asin(ωt) = Asin(2πft)

සටහන

තරංග සඳහා වූ ඉහත සූත්‍රවල sin() යන ත්‍රිකෝණමිතික අනුපාතය වෙනුවට cos() යන අනුපාතයද සමහර පොතපතෙහි යොදා තිබෙනවා.

v = Acos(θ) = Acos(ωt) = Acos(2πft)

ඇත්තටම එම සූත්‍රද නිවැරදිය. කොස් හා සයින් යන අනුපාත දෙකම හැඩයෙන් එක සමාන වන අතර, පවතින එකම වෙනස සයින් ප්‍රස්ථාරයට වඩා කොස් ප්‍රස්ථාරය අංශක 90ක කලාවකින් ඉදිරියෙන් සිටීමයි. ඉතිං කොස් භාවිතා කරන අය දිගටම කොස්ද, සයින් භාවිතා කරන අය දිගටම සයින්ද භාවිතා කළ හැකියි. එහෙත් එක් අනුපාතයක් යොදා ගෙන ගණනය කිරීම සිදු කරගෙන ගොස්, අතරමැදදී අනෙක් අනුපාතයට පැනීම සිදු නොකළ යුතුය.

දැන් අපට තරංග දෙකක් තිබෙනවානෙ - සංඥා තරංගය හා වාහක තරංගය. පැහැදිලි කිරීමේ පහසුව තකා, සංඥා තරංගයද සයිනාකාර ලෙස සාමාන්‍යයෙන් සලකනවා (සත්‍ය සංඥා හැඩය සයිනාකාර නොවී අක්‍රමවත් වුවත් සූත්‍ර ආශ්‍රයෙන් කෙරෙන පැහැදිලි කිරීම එලෙසම අක්‍රමවත් තරංග සඳහාද වලංගු වන බව සිහිතබා ගන්න). ඒ අනුව එම තරංග දෙක පහත ආකාරයට ඉහත පොදු සූත්‍රය යොදාගෙන නිරූපණය කළ හැකියි.

v_carrier = V_C sin(2πf_Ct)

v_signal = V_S sin(2πf_St)

විස්තාර මූර්ජනයේදී කැරියර් තරංගයේ විස්තාරය සංඥා අගය අනුව විචලනය කරන නිසා, පහත ආකාරයට ඉහත සූත්‍ර දෙක එකතු කළ යුතුය. තවද, හැමවිටම වාහක තරංග විස්තාරයට වඩා සංඥා විස්තාරය කුඩා විය යුතුය (V_sig < V_car). එසේ නොවුණොත් අවසාන මූර්ජිත සංඥාව විකෘති වේවි.

V_modulated = [V_signal + V_C ]sin(2πf_Ct) = [V_S sin(2πf_St) + V_C ]sin(2πf_Ct)

m = AM Modulation Index = V_S / V_C

ලෙස අලුත් රාශියක් අර්ථ දක්වමු. m යන්නම modulating factor හෝ modulating coefficient හෝ degree of modulation යන නම්වලින්ද හැඳින්විය හැකිය. එම මොඩ්‍යුලේෂන් ඉන්ඩෙක්ස් එක ඉහත සූත්‍රයට දැන් ආදේශ කළ විට පහත ආකාරයට ඉහත සූත්‍රය සුලු වේ.

V_modulated = [V_S sin(2πf_St) + V_C ]sin(2πf_Ct) = V_C[1+msin(2πf_St)]sin(2πf_Ct)

ඒඑම් මොඩ්‍යුලේෂන් ඉන්ඩෙක්ස් අගය ප්‍රතිශතයක් ලෙසද දැක්විය හැකිය. එවිට එය percentage of modulation (modulation percentage) ලෙස හැඳින්වේ.

modulation percentage = (modulation index) x 100%

මොඩ්‍යුලේෂන් ඉන්ඩෙක්ස් (හෝ මොඩ්‍යුලේෂන් ප්‍රතිශතය) වැදගත් රාශියකි. m අගය 1ට වඩා වැඩි විට (එනම්, වාහක තරංගයේ විස්තාර අගයට වඩා සංඥාවේ විස්තාර අගය වැඩි විට), මූර්ජිත තරංගය විකෘතියකට ලක් වේ (ඒ කියන්නේ මොඩ්‍යුලේෂන් ප්‍රතිශතය 100% වඩා වැඩි විට මූර්ජිත තරංගය විකෘති වේ). මෙම විකෘති අවස්ථාව overmodulation ලෙස නම් කෙරේ. මීට හේතුව විස්තාර මූර්ජනයේදී වාහකයේ උඩු හා යටි මට්ටම් දෙකම සංඥාවේ හැඩය ගන්නා නිසා, ඉන්ඩෙක්ස් අගය වැඩි වේගෙන යන විට, පහත රූපයේ දැක්වෙන විදියට වාහකයේ උඩු හා යටි පැතිවල සිදුවන විචලනයන් එකිනෙකට ළං වී යම් අවස්ථාවකට පසුව එක උඩ එක යෑමයි. පහත රූපයක රතුපාටින් දක්වා ඇත්තේ එවැනි එක උඩ එක ගිය හෙවත් විකෘතිය ඇති වුණු එක් අවස්ථාවකි. මෙම විකෘතිය රූපයේ පෙනෙනා ලෙස දිගින් දිගටම සිදු වේ.

ඕවර්මොඩ්‍යුලේෂන් නිසා එම ඔරිජිනල් සංඥාව විකෘති වෙනවා පමනක් නොව, වෙනත් අහල පහල ඇති සංඛ්‍යාතවලටද ඉන් බාධා ඇති කරනවා (adjacent channel interference). ඒ කෙසේද? එය ලෙහෙසියෙන් පැහැදිලි කර ගත හැකියි සංඥාව සයිනාකාර යැයි මොහොතකට සිතුවොත්. විකෘතිය නිසා දැන් සංඥාව සයිනාකාර බවින් වෙනස් වෙනවානෙ. එවිට ෆූරියර් න්‍යාය අනුව, එතැන දැන් විවිධ සංඛ්‍යාත රාශියක් පවතිනවා (විකෘතිය නොවුණා නම්, සයිනාකාර බව රැකෙන නිසා, එතැන එම සයිනාකාර තරංගය පමණක් පවතින්නට තිබුණා). ඉතිං විකෘතිය නිසා මෙම අතිරේකව හටගත් සංඛ්‍යාතයන් සාමාන්‍ය ඔරිජිනල් සංඥාවේ සංඛ්‍යාතයට වඩා වැඩිය. මෙම විකෘතිය නිසා හටගත් අතිරේක සංඛ්‍යාතයන් නිසා එම අගයන්ගෙන්ම යුතු සංඛ්‍යාත ඔස්සේ නීත්‍යානුකූලව සිදුවන සන්නිවේදනයට දැන් බාධා එල්ල වෙනවා නේද?

ඕවර්මොඩ්‍යුලේෂන් නිසා ළඟපාත ඇති වෙනත් රේඩියෝ උපකරණවලට adjacent channel interference ඇති වීම splatter ලෙසද හැඳින්වෙනවා. ඇත්තෙන්ම ස්ප්ලැටර් ඇති වන්නේ ඕවර්මොඩ්‍යුලේෂන් නිසා පමණක් නොවේ. වෙනත් ඕනෑම හේතුවක් නිසා යම් ඔරිජිනල් සංඥාවක හැඩය විකෘති වුවොත් එවිට ෆූරියර්ට අනුව එතැන අමතරව සංඛ්‍යාතයන් හටගන්නා නිසා, මෙම අමතරව හටගත් තරංගවලින්ද ගැටලු ඇති වෙනවානෙ. ඒවාද ස්ප්ලැටර් වේ.

මෙම විකෘතිය වැලැක්වීමට ඇති ක්‍රමය නම්, සංඥාවේ තිබිය හැකි උපරිම විස්තාර වෝල්ටියතා අගය වාහක වෝල්ටියතා අගයට වඩා අඩු වන සේ තැබීමයි (එනම් මොඩ්‍යුලේෂන් ඉන්ඩෙක්ස් අගය 1ට අඩුවෙන් තැබීමයි). සාමාන්‍යයෙන් සංඥා වෝල්ටියතාවේ උපරිම අගය හමුවන්නේ බොහෝම ඉඳහිටය. වැඩි කාලයක් එම සංඥා වෝල්ටියතාව අඩු අගය පරාසයකයි පවතින්නේ (උපමාවකින් මෙම තත්වය ඔබේ ඇවිදීමට සමාන කළ හැකියි; ඔබට යම් උපරිම වේගයකින් ඇවිදිය හැකි වුවත්, සාමාන්‍යයෙන් එම උපරිම වේගයෙන් නෙමෙයිනෙ ඇවිදින්නේ).

සටහන

ඉඳහිටනෙ උපරිම සංඥා අගයන් මතු වන්නේ, එනිසා එවැනි අවස්ථා නොසලකා හැර සාමාන්‍යයෙන් වැඩිපුරම කාලයක් පවතින සංඥා අගයට ගණනය කරමු යැයි සිතීම වැරදිය. එය විදුලිසංදේශ රීතිවලට පටහැනිය. හැමවිට ඉඳහිට හෝ ඇතිවිය හැකි ස්ප්ලැටර් ඇති නොවන තැනට වගබලා ගත යුතුය. එසේ නැති වුවොත් බොහෝ දෙනෙකු විසින් ඉඳහිට තම තමන්ගේ සම්ප්‍රේෂක උපකරනවලින් ස්ප්ලැටර් ඇති කළොත්, පිරිස වැඩි නිසා, හැමවිටම මුලු සන්නිවේදනය ජාලයම ස්ප්ලැටර්වලින් පිරී යනු ඇත. එවිට කිසිවෙකුටත් සන්නිවේදනය කිරීමට නොහැකි වෙනවා නේද?

මෙමඟින් ඕවර්මොඩ්‍යුලේෂන් විකෘතිය වැලකුණත්, අලුතින් යම් ගැටලුවක් දැන් මතු වේ. එනම් වැඩි කාලයක් පුරාවට ඉන්ඩෙක්ස් අගය 1ට බොහෝ කුඩා අගයක් සේ පැවතීමයි. මෙම අගය 1ට වඩා වැඩි නොවීම වැදගත් වන්නා සේම, එම අගය 1ට වඩා බොහෝ අඩු වීමද හොඳ නැත. එවිට එය විදුලි ශක්තිය අපතේ හැරීමක් හෙවත් අකාර්යක්ෂම බවක් ඇති කරයි (ඒ ගැන සුලු මොහොතකින් ඔබට පෙනේවි). ඉතිං අප උත්සහ කළ යුත්තේ 1ට අනිවාර්යෙන් අඩු, එහෙත් 1ට පුලුවන් තරම් ආසන්න අගයක මෙම අගය පවත්වාගෙන යෑමටයි. මේ සඳහා compression circuit නම් පරිපථ කොටසක් අවශ්‍ය නම් එකතු කළ හැකියි. සංඥාව මූර්ජකයට යොමු කිරීමට පෙර කම්ප්‍රෙෂන් පරිපථය එකතු කළ යුතුය. එමඟින් කෙරෙන්නේ අඩු සංඥා වෝල්ටියතා අගයන් මොඩ්‍යුලේෂන් ඉන්ඩෙක්ස් අගය 1 නොඉක්මවා යන පරිදි ඉහල දැමීමයි.

ඉහතදී ලබා ගත් V_modulated = [V_carrier + V_C ]sin(2πf_Ct) = [V_S sin(2πf_St) + V_C ]sin(2πf_Ct) යන සමීකරණය ප්‍රසාරණය කළ හැකියි පහත ආකාරයට.

V_modulated = [V_carrier + V_C ]sin(2πf_Ct) = V_S sin(2πf_St)sin(2πf_Ct) + V_C sin(2πf_Ct)

sinAsinB = cos(A-B)/2 – cos(A+B)/2 යන ත්‍රිකෝණමිතික සාම්‍යය ඉහත ප්‍රසාරිත සමීකරණයට යෙදූ විට, පහත ආකාරයට එය තවත් සුලු කළ හැකියි.

ඉහත සමීකරණයෙන් විස්තාර මූර්ජනය ගැන ඉතාම වැදගත් තොරතුරු කිහිපයක් හෙලි කරනවා. එම සමීකරණයේ = ට දකුණු පස පද 3ක් තිබේ. ඉන් V_C sin(2πf_Ct) යන පදයෙන් කියවෙන්නේ කුමක්දැයි සිතා බලන්න. එය ඍජුවම වාහක තරංගය නේද? ඔව්. ඒ කියන්නේ මූර්ජිත සංඥාවේ එක් කොටසක් ලෙස වාහක තරංගය නොවෙනස්වම පවතිනවා.

ඉතිරි පද දෙක කොස් අනුපාතවලින් පැවතියත්, සයින් මෙන්ම කොස්වලින්ද තරංග සමීකරණය පෙන්විය හැකි බව ඉහතදී අප ඉගෙන ගත්තා. එහෙත් මෙම කොස් පද නිකංම ආවේ නැත. සුදුසු ගණිත සූත්‍ර හා රීතින් යොදා සුලු කිරීම් කරන විටයි ඒවා මතු වූයේ. එනම්, එය ගණිතමය සුලු කිරීම්වල ප්‍රතිපලයක් ලෙස මතු වූ ඒවාය. එනිසා සයින් අනුපාත සමග මුලින්ම සුලු කිරීම පටන් ගෙන නිකංම මගේ හිතුමනාපේ සයින්වලින් කොස්වලට මාරු වූවා නොවෙයි (හිතුමනාපේ එසේ මාරු විය නොහැකි බවත් මා මුලින් පැවසුවා).

මෙම කොස් අනුපාත සහිත පද දෙකෙහි වැදගත්කම කුමක්ද? ඇත්තටම අපගේ සංඥාව ගැබ්ව පවතින්නේ මෙම පද දෙකෙහි තමයි. V_C sin(2πf_Ct) යන පළමු පදයේ අපේ සංඥාවේ කිසිම කොටසක් ගෑවිලාවත් තිබුණේ නැහැ නේද? පළමු පදය නිකංම වාහකය පමණයි. එහෙත් පසුවට ඇති V_Scos2π(f_C+f_S)/2 හා V_Scos2π(f_C-f_S)/2 පද දෙකෙහිම අපේ සංඥා සංඛ්‍යාතය (f_S) ගැබ්ව පවතිනවා පේනවාද? එක් පදයක (f_C + f_S) ලෙසත්, අනෙක් පදයෙහි (f_C - f_S) ලෙසත් පවතිනවා. ඒ කියන්නේ එක් පදයක සංඥා සංඛ්‍යාතය වාහක තරංගයට එකතු වීද, අනෙක් පදයෙහි වාහක තරංගයෙන් අඩු වීමක් ලෙසද පවතිනවා. මූර්ජනය නිසා ඔරිජිනල් සංඥාව ඉහල සංඛ්‍යාතයකට ඔසවා තැබෙන බව ගණිතානුකූලව දක්වන්නට වන්නේ එහෙමයි. උදාහරණයක් ලෙස, සංඥා සංඛ්‍යාතය හර්ට්ස් 100 හා වාහක සංඛ්‍යාතය කිලෝහර්ට්ස් 2000 හෙවත් හර්ට්ස් 2,000,000 නම්, මූර්ජනයෙන් පසු අපේ සංඥාව හර්ට්ස් 2000000 – 100 = 1,999,900 හෙවත් කිලෝහර්ට්ස් 1999.9 හා හර්ට්ස් 2000000 + 100 = 2,000,100 හෙවත් කිලෝහර්ට්ස් 2000.1 ලෙස දෙයාකාරයෙන්ම පවතී. තවද, මේ පද දෙකෙහිම විස්තාර අගය ඔරිජිනල් සංඥා අගයෙන් භාගයක් (V_S/2) ලෙසයි පවතින්නේ.

ඇත්තටම අපට අවශ්‍ය කරන්නේ (f_C + f_S) සහිත පදය හෝ (f_C – f_S) සහිත පදය පමණි (සමීකරණ හා රූප සටහන්වල සංඥාව signal wave frequency අර්ථයෙන් f_S යන්න ලැබන අතර, එයම modulating wave frequency අර්ථයෙන් f_m ලෙසද දැක්විය හැකිය). එහෙත් ගණිත සමීකරණය අනුව පේනවා එකක් වෙනුවට දෙකක්ම ලබා දී තිබෙන බව. ඔබට හිතෙයි ඉතිං හොඳයිනෙ කියා. එහෙත් එය අනවශ්‍ය මෙන්ම අකාර්යක්ෂම තත්වයකි. ඊට යෙදිය හැකි පිලියම පසුවට කියා දෙන්නම්.

එනිසා, මතක තබා ගන්න සාමාන්‍ය විස්තාර මූර්ජනය නිසා අපගේ ඔරිජිනල් සංඥාව එක් ඉහල සංඛ්‍යාතයකට නොව, ඉහල සංඛ්‍යාත දෙකකම රඳවනවා (ඉහත උදාහරණයේ ගණනය කර පෙන්නුවා සේ). මෙම තත්වය රූපමය වශයෙන් අපූරු ක්‍රමයකින් නිරූපණය කළ හැකියි. කිසිදු සංඥාවක් නැති විට වාහක තරංගයේ උස ඒකාකාරවනෙ පවතින්නේ. 0 යන අගය මැදි කොට ගෙන උඩටත් යටටත් වාහකයේ විස්තාරය විහිදේ. එහෙත් සංඥාවක් පවතින විට, එය ඉහත ආකාරයට එකතු කිරීමක් හා අඩු කිරීමක් ලෙස පැවති අවස්ථා දෙක, මෙම වාහක තරංගයේ ඉහල හා පහල මුදුන්වල පහත රූපයේ ආකාරයට දැක්විය හැකිය. ඔබ ඒඑම් මූර්ජනය ගැන දැක තිබෙන සියලුම පහත ආකාරයට අඳින්නේ ඇයි කියා දැන් ඔබට වැටහිය යුතුය.

සංඥාවක් නැති විටක වාහකය ස්ථාවරව v_C විස්තාරය සහිතව දිගටම පවතිනවා. එහෙත් සංඥාවක් ඊට එකතු වන විට සංඥාවේ විස්තාරය (v_m) නිසා වාහක විස්තාරය උඩිනුත් යටිනුත් විචලනය වෙනවා. පැහැදිලි කිරීම සඳහා උඩු පැත්තේ සිදු වන දේ පමණක් මොහොතකට සලකමු. සංඥාවේ උපරිම විස්තාරය (v_m) පවතින විට, එම අගය වාහක විස්තාර අගයට දැන් එකතු වි (v_C+v_m) රූපයේ පෙනෙන ලෙස සමස්ථ විස්තාර අගය ඉහල යනවා. එලෙසම සංඥාව අවම අගය ගන්නා විට (යට පැත්තෙන් උපරිම විස්තාර අගය ගන්නා විට), දැන් සමස්ථ විස්තාර අගය වන්නේ වාහක විස්තාර අගයෙන් සංඥා විස්තාර අගය අඩු කළ විට ලැබෙන අගයයි (v_C-v_m). ඉතිං මෙම දේම වාහකයේ යටි පැත්තටත් එලෙසම සිදු වෙන බව ඉහත රූපයෙන් පෙන්වා දෙනවා. ඒ කියන්නේ ගණිත සූත්‍රවලින් පැවසූ දේ දැන් රූපමය ආකාරයෙන් සරලව පෙන්වා දී තිබෙනවා.

සටහන

ඉහත රූපයේ (modulation) envelope යන වචනය ගැනද යමක් කිව යුතුය. එන්වෙලොප් යන්නෙහි සාමාන්‍ය තේරුම ලියුම් කවරය යන්නනෙ. ලියුම් කවරයකින් කෙරෙන්නේ යමක් (ලියුමක්) ආවරණය කිරීමනෙ. තාක්ෂනයේදී යම් සංඥාවක ඉහත කඩ ඉරිවලින් දක්වා ඇති පරිදි එම සංඥා හැඩය පෙන්වන විට, ඊටද කියන්නේ එන්වෙලොප් කියාය. එය හරියට ලියුම් කවරයෙන් ලියුම ආවරණය කරන්නා සේ, සමස්ථ සංඥාව ආවරණය කරගෙන සිටී.

මෙම පද දෙක පවතින්නේ අපූරු රටාවකටය. එනම්, වාහක සංඛ්‍යාතය දෙපැත්තේ වාහකයට එකම දුරිනුයි පවතින්නේ. යමක් මැදි කොට ඊට සමාන දුරින් මෙලෙස රාශි දෙකක් පිහිටන විට, එක් රාශියක් අනෙකෙහි ප්‍රතිබිම්භය (image) කියා කියනවා. ඒ අනුව (f_C – f_S) යන්න (f_C + f_S) හි ප්‍රතිබිම්භය වේ (අවශ්‍ය නම්, (f_C + f_S) යන්න (f_C – f_S) හි ප්‍රතිබිම්භය ලෙසද සැලකිය හැකිය). ප්‍රතිබිම්භ යන වචනය මීට අදාල කර ගෙන තිබෙන්නේ කන්නාඩියක් ඉදිරියෙන් යමක් තැබූ විට, එහි ප්‍රතිබිම්භය කන්නාඩිය තුල පෙනෙන ආකාරයටම එක් රාශියක සිට අනෙක් රාශිය පවතින නිසාය.

මෙතෙක් සංඥාව සඳහා එක් සයිනාකාර තරංගයක් පමණක් යොදා ගෙනය ඉහත ආදර්ශන සෑදුවේ. ප්‍රායෝගිකව සංඥාවක් යනු සංඛ්‍යාත පරාසයක්නෙ. ඉතිං එවැනි ප්‍රායෝගික සංඥාවක් සඳහා පහත ආකාරයටයි ඉහත රූපය ඇඳිය යුත්තේ. ඒ කියන්නේ වාහක සංඛ්‍යාතය මැදිකොට ගෙන, ඊට උඩින් හා යටින් (එනම්, වාහකයට දකුණු පැත්තෙන් හා වම් පැත්තෙන්) සංඥා බෑන්ඩ්විත් (පරාස) 2ක් පවතී.

මෙම පරාස දෙක sidebands ලෙස හැඳින්වේ. ඉන් (f_C – f_S) යන්න වාහක සංඛ්‍යාතයට පහලින් තිබෙන නිසා, ඊට Lower Sideband (LSB) ලෙසත්, (f_C + f_S) යන්න වාහකයට ඉහලින් තිබෙන නිසා, ඊට Upper Sideband (USB) ලෙසත් කියා කියනවා. නැවතත් මා කියන්නේ LSB හා USB දෙකෙහිම එකම සංඥාව ගැබ්ව පවතින බව මතක තබා ගත යුතු බවයි.

දැන් බලමු ඒඑම් සංඥාවක විදුලි ශක්තිය ගබඩා වී පවතින්නේ කෙසේද කියා. ඉහත පැහැදිලි කළ සේ, මූර්ජිත අවසන් සංඥාවේ කොටස්/පද 3ක් තිබුණි (වාහකය, LSB, USB). ඒ කියන්නේ අප භාහිරින් සැපයූ මුලු විදුලි ජවය එම කොටස් තුන අතරේ බෙදී යයි.

මුලු ජවය = වාහකය තුල පවතින ජවය + LSB තුල පවතින ජවය + USB තුල පවතින ජවය

ඉහත සමීකරණයෙන් බැහැනෙ ගණනය කිරීමක් සිදු කරන්න (එය නිකංම පද අතර සම්බන්දතාව වචනයෙන් පෙන්වීමක් පමණි). අපට අවශ්‍ය වන්නේ සුලු කර විදුලි ශක්තින්/ජවයන් ගණනය කළ හැකි සූත්‍රයකි. මූර්ජිත තරංගයේ වෝල්ටියතා අගයන් මීට පෙර ලබා ගත් සමීකරණයෙන් දැක්වේ. මා නැවත එම සමීකරණය පහත දක්වනවා. මෙම සමීකරණය ආශ්‍රයෙන් පුලුවන් විදුලි ජවය ගණනය කළ හැකි සමීකරණයක් ගොඩනඟා ගන්නට.

ඉහත සමීකරණයෙහි V_C හා V_S යනු peak voltage අගයන්ය. මෙම පීක් වෝල්ටියතාවන් rms voltage අගයන් බවට පරිවර්තනය කරගමු. සත්‍ය ජවයන් ගණනය කරන්නට අපට අවශ්‍ය rms voltage අගයන්ය. පීක් වෝල්ටියතාවක් 2හි වර්ගමූල අගයෙන් හෙවත් 1.414 යන අගයෙන් බෙදීමෙන් rms වෝල්ටියතාව ලබා ගත හැකියි. ඒ අනුව ඉහත සමීකරණයම rms අගයන් සහිතව පහත ආකාරයට ලිවිය හැකිය.

සටහන

යම් රාශියක් තරංගයක් ආකාරයට දෝලනයක් සිදුවන විට, එහි විස්තාරය කාලයත් සමග වෙනස් වෙනවා. 0 මධ්‍ය රේඛාවේ සිට උපරිම විස්තාර අගය peak (කුලු) අගය ලෙස හැඳින්වේ. එලෙසම පහල කුලු අගයේ සිට ඉහල කුලු අගයට ඇති මුලු විස්තාර අගය peak-to-peak අගය ලෙස හැඳින්වේ. හැමවිටම පීක් අගය පීක්ටුපීක් අගයෙන් හරි අඩකි. පීක් හා පීක්ටුපීක් අගය යන දෙකම නිරන්තරයෙන්ම කාලයත් සමග වෙනස් වන බව අමුතුවෙන් කිව යුතු නැහැනෙ. එම අගය වෝල්ටියතාව විය හැකිය; විදුලි ධාරාව හෝ විදුලි ජවය විය හැකිය. එසෙත් නැතිනම්, ආලෝක ත්‍රීව්‍රතාව, පීඩනය, හෝ වෙනත් ඕනෑම රාශියක් විය හැකිය (වැදගත් වන්නේ රාශිය කුමක්ද යන්න නොව, එම රාශිය තරංග ආකාරයෙන් තම අගය කාලයත් සමග විචලනය කර ගැනීම පමණි). එහෙත් අප මෙම පාඩම්වල සලකා බලන්නේ විදුලි වෝල්ටියතාව යන රාශියයි. ඒ අනුව, පහත රූපයේ පීක් වෝල්ටේජ් (V_p), පීක්ටුපීක් වෝල්ටේජ් (V_pp), හා ආර්එම්එස් වෝල්ටේජ් (V_RMS) දැක්වේ.

නිකමට සිතන්න තරංග ආකාරයේ යම් විදුලි බලයක් හීටරයක් හරහා යවනවා කියා. එවිට, හීටරය රත් වන්නේද එම විදුලි තරංගයේ හැඩයට අනුරූපවයි. එනම්, විදුලි බලය ක්‍රමයෙන් (උපරිම අගය දක්වා) වැඩි වේගෙන යන විට, හීටරයද ක්‍රමයෙන් රත්වීමේ වේගය වැඩි කරනවා. ඉන්පසු විදුලි තරංගය නැවත 0 කරා ක්‍රමයෙන් අඩු වන විට හීටරයද ඊට අනුරූපව රත්වීමේ වේගය අඩු කර ගන්නවා. හීටරය වෙනුවට බල්බයක් සවි කළේ නම්, විදුලිය විචලනය වන ආකාරයටම බල්බයේ දීප්තිය අඩු වැඩි වේවි.

එහෙත් එම හීටරය හරහා ඩීසී විදුලියක් (එනම් කාලයත් සමග විචලනය නොවන විදුලියක්) යවන විට, එවැනි තත්වයක් ඇති නොවී, හීටරය දිගටම එකම ආකාරයට/වේගයට රත්වී ගෙන පවතිනවා. බල්බයක් නම්, එකම දීප්තියකින් දැල්වීගෙන තිබේවි.

අපට හැකියි විචලනය වන විදුලියකින් ලැබෙන ප්‍රතිපලය ඩීසී විදුලියකින් ලැබෙන ප්‍රතිපලයකට සමාන කරන්නට. එහෙත් මෙවිට විදුලියේ පීක් අගය 2හි වර්ගමූල අගයෙන් (1.414න්) බෙදිය යුතු වෙනවා. මෙයම කියත හැකියි පීක් අගය 1/1.414 හෙවත් 0.707 යන අගයෙන් වැඩි කරනවා කියාද. මෙලෙස ලැබෙන අගයට අපිට දැන් පීක් අගය කියා කියන්න බැහැනෙ. එය rms (root mean square) අගය ලෙසයි දැන් හඳුන්වන්නේ.

ලංකාවේ ප්‍රධාන විදුලියේ (එනම් ගෙවල්වලට ලැබෙන විදුලියේ) වෝල්ටියතාව 240 ලෙස පවසන්නේ ඇත්තටම මෙම ආර්එම්එස් වෝල්ටියතාවයි. ඒ කියන්නේ එම විදුලියේ කුලු වෝල්ටියතාව 240 x 1.414 = 340 ක් පමණ වේ.

සයිනාකාර තරංග සඳහා ඉහත අගයන් අදාල වුවත්, විචලනය සිදු වන්නේ square wave හෝ sawtooth හෝ triangle හෝ වෙනත් ඕනෑම හැඩයකින් නම් ඉහත අගයන් භාවිතා කළ නොහැකිය. එක් එක් හැඩයන් සඳහා ගුණ කළ යුතු වෙනස් වෙනස් ගුණක අගයක් ඇත (අවශ්‍ය නම්, එම අගයන් ගැන සොයා බලන්න). එහෙත් අපට හැමවිටම වාගේ rms සෙවීමට සිදුවන්නේ සයිනාකාර හැඩයටයි. එනිසා ඉහත 0.707 වැනි අගය ගැන දැන සිටීම වුවද ප්‍රමාණවත්ය.

වෝල්ටියතාවක් ජවය = වෝල්ටියතාව²/ප්‍රතිරෝධය (P = V²/R) යන සූත්‍රයට අනුව ජවයක් බවට පරිවර්තනය කළ හැකියි. සයින් හා කොස් අනුපාතයක් හැමවිටම +1ත් -1ත් අතර අගය පරාසයක් තුල දෝලනය වේ. ඉතිං, ඉහත සමීකරණයේ සයින් හා කොස් අනුපාත කොටස් නොසලකා හැරිය හැකියි. ඒ කියන්නේ සයින් හා කොස් අනුපාත ඇති ස්ථානවලට 1 යන අගය ආදේශ කළ හැකියි. එවිට, එම සමීකරණය කාලයත් සමග අගය වෙනස්වීම නවතා දමයි. ඒ වෙනුවට උපරිම අගය සහිත ස්ථාවර (ඩීසී) අවස්ථාව පෙන්වන සමීකරණයක් බවට එය පත් වේ. අපට දැන් කරන්නට අවශ්‍යත් එයම තමයි. ඉහතදී අගයන් rms බවට පත් කර ගත්තේද මෙම තත්වයට මුහුණ දීමට තමයි. එය හරියට සුදුසු වන්දියක් ලබා දී සේවකයකු ආයතනයකින් ඉවත් කළා වගේ වැඩකි (එනම් ඔහුට අසාධාරණයක් වූයේ නැත). සයින් කොස් පද ඉවත් කර, රාශින් rms කිරීම මඟින් සිදු කළේ ඒසී හෙවත් විචලනය වන විදුලිය ඩීසී හෙවත් ස්ථාවර වන විදුලියක් බවට පත් කිරීමයි. එනිසා ඒසී විදුලියක් වෙනුවට දැන් අප මෙතැන් සිට කටයුතු කරන්නේ ඩීසී විදුලියක් සමග වන අතර, ඉන් කිසිදු “අසාධාරණයක්” සිදු නොවන්නේ ඉහත ආකාරයට “සුදුසු වන්දියක්” ගෙවා ඇති නිසාය (තවත් විදියකින් කියතොත්, ඒසී ගණිතානුකූලව ඩීසී බවට පත් කර ඇත).

ඉහත ආකාරයට කාලය සමග විචලනය වීම (සාධාරණ ලෙස) නවතා දමා, මූර්ජිත සංඥාවේ විදුලි බලය දැන් පහසුවෙන්ම පහත ආකාරයට ගණනය කළ හැකිය. පහත සුලු කිරීම්වල අවසානයේ ලැබී තිබෙන සමීකරණය තමයි අපට අවශ්‍ය වන්නේ. මොඩ්‍යුලේෂන් ඉන්ඩෙක්ස් අගය මත ඒඑම් මූර්ජනය මඟින් ලැබෙන අවසාන සංඥාවේ ජවයන් දැන් ගණනය කළ හැකියි.

දැන් අපි ගණනය කිරීම් කිහිපයක් සිදු කරමු. වාහක තරංගයේ ජවය වොට් 50 නම්, හා මොඩ්‍යුලේෂන් ඉන්ඩෙක්ස් අගය 1 නම්, අවසාන මූර්ජිත සංඥාවේ මුලු ජවය කොපමණද?

මුලු ජවය = 50(1+1²/2) = 50 x 1.5 = 75W

මූර්ජිත සංඥාවේ මුලු ජවය වොට් 75කි. මින් 2/3ක් වන වොට් 50ක්ම වැය වී තිබෙන්නේ වාහක තරංගය සඳහාය. එවිට සයිඩ්බෑන්ඩ් 2 සඳහා 75 – 50 = 25 වොට් ප්‍රමාණයකි ඉතිරිවන්නේ.

ඉහත සලකා බැලූ ගැටලුව මෙසේද ඉදිරිපත් කළ හැකියි. ඒඑම් ක්‍රමයට සංඥා යැවීම සඳහා වැය වන මුලු ජවය වොට් 75ක් නම්, ඉන් වොට් P_tot / (1+m²/2) = 75/(1+1²/2) = 50 ක ප්‍රමාණයක් වාහකය සඳහා වැය වේ. එවිට, ඉතිරිය වන P_tot – P_carrier = 75-50 = වොට් 25 ප්‍රමාණය සයිඩ්බෑන්ඩ් දෙක සඳහා වැය වේ.

පෙර සේම වාහක තරංගයේ ජවය වොට් 50 ලෙස ගෙන, මොඩ්‍යුලේෂන් ඉන්ඩෙක්ස් අගය 0.5 නම්, නැවත පෙර සේම මූර්ජිත සංඥාවේ මුලු වොට් ගණන ගණනය කරමු.

මුලු ජවය = 50(1+0.5²/2) = 50 x 1.125 = 56.25W

දැන් සයිඩ්බෑන්ඩ් සඳහා පවතින්නේ වොට් 6.25කි. මින් පෙනෙනවා මොඩ්‍යුලේෂන් ඉන්ඩෙක්ස් අගය අඩු වන්නට වන්නට සයිඩ්බෑන්ඩ් සඳහා වෙන් වන වොට් ගණන අඩු වෙන බව. ඉතිං එහි ඇති ප්‍රශ්නය කුමක්ද? විශාල ප්‍රශ්නයක් ඇත. වාහක තරංගයේ කිසිදු බුද්ධියක්/සංඥාවක් නැහැනෙ. එහෙත් මුලු ජවයෙන් වැඩිම ප්‍රමාණයක් වැය වී තිබෙන්නේ ඒ “කමකට නැති” වාහකය වෙනුවෙනුයි. ඒ කියන්නේ වාහකයා මෙහිදී “සුදු අලියෙකි”. මිශ්‍රකයට එන්න පෙර අවස්ථාවලදී වාහකය යනු ඉතාම වැදගත් නැතිවම බැරි සහයකයෙක් වුවත් (වාහකයක් නැතිනම් කිසිදු මූර්ජන ක්‍රමයක් පවතින්නේද නැත), මිශ්‍රකයෙන් පසුව වාහක තරංගය නාස්තිකාර කරදරකාරයෙකි. සත්‍ය තොරතුරු ගබඩා වී පවතින සංඥාව පවතින්නේ සයිඩ්බෑන්ඩ් වලයි. එහෙත් ඒ සඳහා කුඩා ජවයක් පමණයි වෙන් වන්නේ. එය කොතරම් අකාර්යක්ෂමද කියා සිතා බලන්න.

පෙරදී ඉගෙන ගත්තා මොඩ්‍යුලේෂන් ඉන්ඩෙක්ස් අගය 1 ලෙස පවත්වාගෙන යා හැකි නම් ප්‍රසස්ථම මූර්ජන මට්ටම ලැබෙන බව. එය 1ට වැඩි වූවොත් ඉහත සූත්‍රය අනුව වාහකයට වෙන් වන ජවය අඩුවී කාර්යක්ෂම වනු ඇත. එහෙත් එවිට නැවත නිවැරදි කළ නොහැකි තරමේ විකෘතියක්ද එමඟින් වෙනත් සංඥාවලට බාධාවක් (ස්ප්ලැටර්) ඇති වේ. එලෙසම එම අගය 1ට වඩා අඩු වන්නට වන්නට මූර්ජනය අකාර්යක්ෂම වන බවද පෙනෙනවා නේද?

ඒ කියන්නේ ඉහත ආකාරයට AM මූර්ජන ක්‍රමය එතරම් කාර්යක්ෂම මූර්ජන ක්‍රමයක් නොවේ. මෙම අකාර්යක්ෂම මූර්ජන ක්‍රමය Double Sideband with Full Carrier (DSB-FC) ලෙස හැඳින්වේ. එහි තේරුම සයිඩ්බෑන්ඩ් දෙකද සම්පූර්ණ වාහක තරංගයත් එකට අවසාන මූර්ජිත තරංගයේ පවතිනවා යන්නයි. එය Original AM ක්‍රමය ලෙසද හැඳින්විය හැකියි. මෙම අකාර්යක්ෂමතා තිබුණත්, DSB-FC පරිපථයට අවශ්‍ය කරන උපාංග ප්‍රමාණය අඩු වේ.

ඉහත ඔරිජිනල් ඒඑම් ක්‍රමයේ තිබූ අකාර්යක්ෂමතා කිහිපයක් ඔබ දුටුවා. ඉන් ප්‍රමුඛ වූයේ වාහකය වෙනුවෙන් ජවයෙන් වැඩිම පංගුවක් නිකරුණේ වැය කිරීමයි. අවසාන මූර්ජිත සංඥාවෙන් වාහකය සම්පූර්ණයෙන්ම ඉවත් කළ හැකි නම් හෝ වාහකය සඳහා වැය වූ ජවය අතිවිශාල ප්‍රතිශතයකින් අඩු කළ හැකි නම් එම අකාර්යක්ෂමතාව ඉවත් කළ හැකියි නේද? අනෙක් අකාර්යක්ෂමතාව වන්නේ එකම බුද්ධි සංඥාව සයිඩ්බෑන්ඩ් 2කම පැවතීමයි. එවිට, ඉන් එක් සයිඩ්බෑන්ඩ් එකක් ඉවත් කළ හැකි නම්, එම අකාර්යක්ෂමතාවත් ඉවත් කළ හැකියි නේද? ඇත්තටම මෙම අකාර්යක්ෂමතා ඉවත් කරමින් ඒඑම් ක්‍රමයෙහිම ප්‍රභේද ගණනාවක්ම බිහි කර ඇත. මේ සෑම ප්‍රභේදයක්ම ඔරිජිනල් ඒඑම් ක්‍රමයට වඩා කාර්යක්ෂම වේ.

එම කාර්යක්ෂම ඒඑම් ප්‍රභේද වන්නේ DSB-SC, SSB-FC, SSB-SC (USB/LSB), SSB-RC, VSB, ISB වේ. ඒ එක් එක් ප්‍රභේදය ගැන වෙන වෙනම දැන් සොයා බලමු. ඔරිජිනල් ඒඑම් ක්‍රමය හා ඉන් ව්‍යුත්පන්න අනෙක් කාර්යක්ෂම ප්‍රභේද සියල්ලෙහිම පොදු හොඳ ලක්ෂණයක් තිබෙනවා අනෙක් ප්‍රධාන මූර්ජන ක්‍රම දෙක වන FM හා PM ට වඩා. එනම්, මෙම මූර්ජන ක්‍රම දෙකට වඩා හැමවිටම අඩු සංඥා බෑන්ඩ්විත් එකක් තමයි ඒඑම් ක්‍රමවලට අවශ්‍ය වන්නේ. තනි සයිඩ්බෑන්ඩ් එකක් පමණක් යොදා ගන්නා විට, ඊට අවශ්‍ය කරන්නේ ඔරිජිනල් සංඥාවේ තිබූ බෑන්ඩ්විත් එකට සමාන සංඛ්‍යාත පරාසයකි. සයිඩ්බෑන්ඩ් දෙකම යොදා ගන්නා විටදී ඒ වගේ දෙගුණයක සංඛ්‍යාත පරාසයක් අවශ්‍ය කෙරෙනවා. එසේ දෙගුණකයක් අවශ්‍ය වුවත්, එය තවමත් FM, PM ක්‍රම දෙකෙහිදී අවශ්‍ය කරන සංඛ්‍යාත පරාසයට වඩා අඩුය.

Double SideBand with Suppressed Carrier (DSB-SC)

මෙය සමහරවිට නිකංම DSB ලෙසද හඳුන්වනවා. මෙහිදී මූර්ජිත තරංගයේ තිබෙන වාහක තරංගය සම්පූර්ණයෙන්ම යටපත් කර දමනවා (suppress). ඒ කියන්නේ සම්ප්‍රේෂනය කරන අවසාන මූර්ජිත සංඥාවෙහි දැන් තිබෙන්නේ සයිඩ්බෑන්ඩ් දෙක පමණි. මින් විදුලි බලය විශාල ඉතුරුවීමක් සිදු වෙනවා. ඉහතදී අප දුටුවා මොඩ්‍යුලේෂන් ප්‍රතිශතය 100%ක ප්‍රශස්ත මට්ටමේ තිබෙන විට පවා සපයන විදුලියෙන් තුනෙන් දෙකක්ම වැය වූයේ වාහකය සඳහාය. ඉතිං මෙම වාහකය ඉවත් කර දැමුවාම එම විදුලි ප්‍රමාණය ඉතිරි වෙනවානෙ.

ඉහත රූපය පරිස්සමින් බලන්න. බැලූබැල්මට සාමාන්‍ය ඒඑම් මූර්ජිත සංඥාවේ හැඩයම පෙනුනත්, එතැන විශාල වෙනසක් ඇත. එහි රතුපාටින් (හෝ කොලපාටින්) දක්වා ඇත්තේ DSB-SC බුද්ධි සංඥාවයි. 0 තිරස් රේඛාවට ඉහලින් හා පහලින් මෙම බුද්ධි සංඥාව දැන් විහිදී පවතී. මීට පෙර හමුවූ සාමාන්‍ය ඒඑම් මූර්ජිත සංඥාවකදී හැමවිටම 0 තිරස් රේඛාවට ඉහලින් හා පහලින් වෙන් වෙන්වය බුද්ධි තරංගය (එකම සංඥාවේ කොපි දෙකක් ලෙස) පැවතුණේ; කවදාවත් 0 තිරස් රේඛාව කපාගෙන ගියේ නැත; එසේ කපාගෙන ගියා නම් එය ඕවර්මොඩ්‍යුලේෂන් වනු ඇත. එහෙත් DSB-SC හිදී සංඥා කොපි දෙක තිරස් රේඛාව දෙපැත්තේම විහිදී තිබෙනවා.

වොට් 100ක සාමාන්‍ය ඒඑම් ට්‍රාන්ස්මීටරයකින් අපි සිතමු රේඩියෝ සංඥාවක් කිලෝමීටර් 500ක් ඈතට ගමන් කළා කියලා. වොට් ගණන වැඩි කරන විට මෙම දුර ප්‍රමාණය තවත් වැඩි වන බව අමුතුවෙන් කිව යුතු නැහැ. එලෙසම වොට් ගණන අඩු කළොත් මෙම දුර ප්‍රමාණය අඩු වෙනවානෙ. එහෙත් එම සංඥාව DSB-SC ක්‍රමයට විසුරුවා හැරියොත් එම දුර ප්‍රමාණයම තරංගය ගමන් කරාවි, නමුත් ඒ සඳහා දැන් වැය වන්නේ වොට් 33ක් පමණ වේ (කැරියර් එකේ වොට් 66 වැය නොවන නිසා). බලන්න එය කොතරම් වටිනවාද කියා. හැමවිටම මෙම මූර්ජන ක්‍රමය සාමාන්‍ය ඒඑම් ක්‍රමයට වඩා විදුලි ජවය භාවිතා කරන්නේ 1/3කි.

ඒ කියන්නේ මෙවැනි කාර්යක්ෂම ඒඑම් ක්‍රමයක් භාවිතා කරන විට, වැය වන විදුලි ජවය අඩු වෙනවා. එවිට, උපකරණ රත් වීම අඩු වෙනවා (එනිසා රත්වීම වැලැක්වීමට යොදන උපක්‍රම අඩුවෙන් යෙදිය හැකියි). ජවය අඩු වන නිසාත්, රත්වීම සමනය කරන උපක්‍රම වැඩිපුර නොයොදන නිසා ට්‍රාන්ස්මීටරය සයිස් එකෙන්ද කුඩා වේ. මේ සියලුම හේතු නිසා උපකරණයේ මිලද අඩු වේ. තවද, කුඩා වීම නිසාත්, රත් වීම අඩු නිසාත්, විදුලිය අඩුවෙන් වැය වීම නිසාත්, මෙම උපකරණ පහසුවෙන් එහා මෙහා ගෙන යා හැකිය (mobile).

එහෙත් මෙම ක්‍රමය සඳහා තවමත් සාමාන්‍ය ඒඑම් ක්‍රමය සඳහා වැය වූ සංඛ්‍යාත පරාසයම වැය වේ (එනම් සංඥා බෑන්ඩ්විත් අගය මෙන් දෙගුණයක්) මොකද වාහකය ඉවත් කළත් තවමත් සයිඩ්බෑන්ඩ් දෙකම සම්ප්‍රේෂනය කරන නිසා.

Single SideBand (SSB)

මෙහිදී එක් සයිඩ්බෑන්ඩ් එකක් පමණයි සම්ප්‍රේෂනය කරන්නේ. එහි ප්‍රතිපලය වන්නේ ඉහත කතා කළ DSB ක්‍රම දෙකට (සාමාන්‍ය ඒඑම් ක්‍රමය වන DSB-FC හා DSB-SC) වඩා හරි අඩක බෑන්ඩ්විත් එකක් පමණි අවශ්‍ය කරන්නේ. එය විශාලම වාසියකි. එමඟින් වැඩිපුර සංඥා ප්‍රමාණයක් (දෙගුණයක්) සන්නිවේදනය කළ හැකි වෙනවානෙ.

වැඩිපුර සංඥා ප්‍රමාණයක් යැවිය හැකි වීමට අමතරව, මෙම ක්‍රමය DSB ක්‍රමයට වඩා හොඳින් ඝෝෂාවටද ඔරොත්තු දෙයි. ඊට හේතුව, සංඛ්‍යාත පරාසය අඩු නිසා, යම් භාහිර කරදරයක් සංඥාවෙහි “හැප්පෙන්නට” තිබෙන චාන්ස් එක අඩුය. තවදුරටත් උපමාවකින් එය කිව්වොත්, ඔබ යමක් දෙසට ගලකින් ගසන විට, එම දෙය විශාල නම් ඔබේ ගල එහි වැදීමේ චාන්ස් එක වැඩියි නේද (ඒ දෙය කුඩා නම්, ගල වදින්නට තිබෙන හැකියාව අඩුයි)?

සයිඩ්බෑන්ඩ් දෙකක් තිබෙන නිසාත්, ඉන් එකක් අනිවාර්යෙන්ම කපා දමන නිසාත්, කුමන සයිඩ්බෑන්ඩ් එක කපා දැමිය හැකිද? ඇත්තටම දෙකෙන් ඕනෑම එකක් කපා දැමිය හැකියි. පහල සයිඩ්බෑන්ඩ් එක කපා දැමූ විට, ඉහල සයිඩ්බෑන්ඩ් එක සම්ප්‍රේෂනය වන නිසා, එවිට එය Upper SideBand (USB) ක්‍රමය ලෙස නම් කෙරේ. එලෙසම ඉහල සයිඩ්බෑන්ඩ් එක කපා දැමූ විට, එවිට පහල සයිඩ්බෑන්ඩ් එක සම්ප්‍රේෂනය වන බැවින් එය LSB ලෙස නම් කෙරේ.

පරිපථය නිර්මානය කරන කෙනායි තීරණය කරන්නේ කුමන සයිඩ්බෑන්ඩ් එක කපා හරිනවාද කියා. සාමාන්‍යයෙන් වාහක තරංගයේ සංඛ්‍යාතය අඩු අගයක පවතින විට USB ක්‍රමය යොදා ගන්නා අතර, වාහක සංඛ්‍යාතය වැඩි විට LSB යොදා ගැනේ. ඊට හේතුව සරලය. පහලම සංඛ්‍යාත මෙන්ම ඉහලම සංඛ්‍යාත සමග වැඩ කිරීම අපහසුය. ඉතිං තෝරා ගැනීමක් තිබෙන විට, පහල සංඛ්‍යාත වාහක අවස්ථාවලදී, පුලුවන් හැමවිට ඉන් ඉහල අගය සහිත කොටස තෝරා ගැනීමෙන් පහල සංඛ්‍යාතවලින් හැකි තරම් දුරස් විය හැකියිනෙ. එය උපමාවකින් කියතොත්, පොඩි වෙච්ච ඇපල් ගෙඩි ගොඩකින් ඔබට ඇපල් ගෙඩියක් තෝරා ගැනීමට අවශ්‍ය වුවොත්, ඔබ තෝරා ගන්නේ අඩුවෙන්ම සවුත්තු වී තිබෙන එකක්නෙ (ඒ කියන්නේ සවුත්තු බවින් හැකි තරම් දුරස් අවස්ථාවයි ඔබ තෝරා ගන්නේ). එලෙසමයි, ඉහල සංඛ්‍යාත වාහක අවස්ථාවකදී, තෝරා ගන්නේ හැකි තරම් අඩු සංඛ්‍යාත කොටසකි.

මෙම එස්එස්බී ක්‍රමයද ක්‍රම කිහිපයකින් ක්‍රියාත්මක කළ හැකියි. SSB with Full Carrier (SSB-FC) ක්‍රමය මේ අතරින් අඩුවෙන්ම යොදා ගන්නා ක්‍රමයයි. මෙහි එක් සයිඩ්බෑන්ඩ් එකක් සමග වාහකයද කිසිදු වෙනසක් නොකර ගමන් කරවනවා. ඒ කියන්නේ වාහකය සඳහා වැය වන විශාල විදුලිය දැන් නැවත අපතේ යනවා. එහෙත් එක් සයිඩ්බෑන්ඩ් එකක් කපා දැමෙන නිසා කුඩා වොට් ගණනක් ඉතිරි වේවි - සම්පූර්ණ වොට් ගණනින් 15%ක් පමණ (මොඩ්‍යුලේෂන් ඉන්ඩෙක්ස් අගය 1 විට). තෝරා ගන්නා සයිඩ්බෑන්ඩ් එක ගැන ඉහත ඡේදයේදී කියූ කරුණු වලංගු වේ.

වැඩිපුරම යොදා ගන්නා වඩාත්ම කාර්යක්ෂම ක්‍රමය වන්නේ SSB with Supressed Carrier (SSB-SC) වේ. මෙහිදී වාහකයද කපා හැරේ. එවිට විශාල විදුලියක් ඉතිරි වේ. මෙම ක්‍රමයේදී සංඛ්‍යාත පරාසය මෙන්ම විදුලියද ඉතිරිවන නිසා, ඉතාම හොඳ ක්‍රමයකි. P_tot = P_carrier(1+m²/2) යන සූත්‍රය අනුව සපයන විදුලි ජවයෙන් වාහකයට කොපමණ ජවයක් වැය වෙනවාද යන්න සොයා, එමඟින් සයිඩ්බෑන්ඩ් දෙක සඳහා අවශ්‍ය ජවය සොයා, එම අගය 2න් බෙදූ විට එක් සයිඩ්බෑන්ඩ් එකක පවතින ජවය ලැබේ. මෙම අගය තමයි SSB-SC හි ජවය වන්නේ. සාමාන්‍යයෙන් ඔරිජිනල් ඒඑම් ක්‍රමයට වැයවන විදුලි ජවයෙන් 1/6ක් පමණ කුඩා ප්‍රමාණයකුයි SSB-SC සඳහා වැය වන්නේ.

උදාහරණයක් ලෙස, වොට් 100ක් සඳහා මොඩ්‍යුලේෂන් ඉන්ඩෙක්ස් අගය 1 විට, SSB-SC සම්ප්‍රේෂනයක් සඳහා වැයවන ජවය කොපමණද?

P_tot = P_carrier(1+m²/2) අනුව, 100 = P_carrier(1+1²/2) = P_carrier(1.5) → P_carrier = 100/1.5 = 66.7W

එවිට, සයිඩ්බෑන්ඩ් 2 සඳහා වෙන්වන ජවය = P_tot – P_carrier = 100 – 66.7 = 33.3W

එවිට, සයිඩ්බෑන්ඩ් 1ක් සඳහා වෙන්වන ජවය = 33.3/2 = 16.6W

ඉහත ගණනය කිරීම තේරුම්ගත යුත්තේ මෙසේය. සාමාන්‍ය ඒඑම් ක්‍රමය (DSB-FC) යොදා ගත් විට, ඊට වොට් 100ක් අවශ්‍ය වුවත්, SSB-SC යොදා ගත් විට අවශ්‍ය වන්නේ වොට් 16.6කි. එය 16.6/100 = 1/6 ගුණයකි.

ඉහත ආකාරයට එස්එස්බී ක්‍රමය සඳහා වැය වන විදුලි ජවය අපට ගණනය කළ හැකියිනෙ. මෙහිදී වාහකයක් නොමැති නිසාත්, එක් සයිඩ්බෑන්ඩ් එකක් පමණක් තිබෙන නිසා, අවසානයේ සම්ප්‍රේෂනය වන සයිඩ්බෑන්ඩ් එකේ සියලුම විදුලි ජවය ගැප්ව පවතී. එම ජවය හැමවිටම ඉහත සුලු කිරීම්වල දක්වා ඇති පරිදිම rms අගයකි. ඒ විතරක්ද නොවේ; එම ජවය ගණනය කිරීමේදී හැමවිටම සංඥා එන්වෙලොප් එකෙහි උපරිම වෝල්ටියතා අගයන් දෙක අතර වෙනස හෙවත් එන්වෙලොප් එකෙහි පීක්ටුපීක් අගය (Vpp) ගෙන, එය 2න් බෙදා ලැබෙන අගය 0.707න් ගුණ කර rms වෝල්ටියතා අගය ගෙන, අන්න එම අගය මඟිනුයි එහි ජවය සොයන්නේ. මෙලෙස ලැබෙන ජවයට Peak Envelope Power (PEP) යැයි කියනවා. රේඩියෝ රෙගුලාසිවල එස්එස්බී සම්ප්‍රේෂකවල ජවය හැමවිටම වාගේ පවසන්නේ මෙම පෙප් (PEP) අගයෙනි. නැවත මතක් කර දෙන්නේ පෙප් ගණනයේදී සංඥාවේ පවතින විශාලතම පීක්ටුපීක් අගයයි භාවිතා කරන්නේ. එමඟින් අනිවාර්යෙන්ම එස්එස්බී ට්‍රාන්ස්මීටරයෙන් පිටවන ජවය පෙප් අගයට සමාන හෝ අඩුවෙන් තිබෙන බවට ස්ථිරවම කිව හැකියි.

SSB-SC ක්‍රමය ඉතා කාර්යක්ෂම වුවත්, එහි ප්‍රායෝගික ගැටලුවක් ඇත. එනම් එම ක්‍රමයට සංඥාවක් සම්ප්‍රේෂනය කළ පසු, එම සංඥාව ග්‍රහනය කරන උපකරණයේදී නැවත මුල් බුද්ධි සංඥාව ඉන් උකහා ගැනීමේදී ඇති වන අපහසුතාවයි. ග්‍රාහක පරිපථය (receiver) විසින් SSB-SC සංඥාවකින් එහි ගැප්ව ඇති බුද්ධි සංඥාව උකහා ගැනීමට එම ග්‍රාහක පරිපථයේදී සම්ප්‍රේෂනයේදී යොදා ගත් වාහක තරංගය තිබිය යුතු යුතුය. එය තාක්ෂණික අවශ්‍යතාවකි. වාහක තරංගයද විසුරුවා හරින ක්‍රමවලදී එම වාහක තරංගය රිසීවරයට බුද්ධි සංඥාව සමගම ලැබෙනවනෙ. එහෙත් වාහකය විසුරුවා හරින්නේ නැති SSB-SC වැනි ක්‍රමයකදී දැන් ගැටලුවක් ඇති වෙන බව පැහැදිලියි.

ඉතිං, ඊට විසඳුම වන්නේ රිසීවරය තුලම වාහක සංඛ්‍යාතයට සර්වසම අලුත් වාහක තරංගයක් නිපදවීමයි. පහසුවෙන් අපට අවශ්‍ය ඕනෑම සංඛ්‍යාතයක් සහිත තරංගයක් නිපදවීමට ඔසිලේටරයක් තැනිය හැකි නිසා එය එතරම් කජ්ජක් නොවේ යැයි සමහරවිට ඔබට සිතේවි. එහෙත් මෙහි සියුම් කාරණාවක් ඇත. එනම්, එසේ නිපදවන වාහක තරංගය මුල් වාහක තරංගයට හැම මොහොතේම සමාන ලෙස පවතින්නේ නැත. උදාහරණයක් ලෙස, මෙගාහර්ට්ස් 100ක ඔසිලේටරයක් සෑදුවත්, ඉන් හැමවිටම මෙගාහර්ට්ස් 100ම ලැබෙන්නේ නැත. එය මෙගාහර්ට්ස් 99.9999 සිට මෙගාහර්ට්ස් 100.0001 දක්වා අගය පරාසයක් අතර විචලනය විය හැකිය. කොයිල්, කැපෑසිටර්, ක්‍රිස්ටල් වැනි ඔසිලේටර් සෑදීමට ගන්නා ඉලෙක්ට්‍රෝනික් උපාංග ක්‍රියාත්මකව පවතින විට, විවිධ හේතු නිසා, ඔසිලේටරයකින් නිපදවන තරංග සංඛ්‍යාතය එහි තිබිය යුතු අගයට වඩා සුලු වශයෙන් හෝ ඉහල පහල යනවාමයි. එලෙස අපගමනය වීම drift ලෙස හැඳින්වෙනවා. විශේෂයෙන් පරිපථය තිබෙන පරිසර උෂ්ණත්වය වෙනස්වන විට මෙය සිදු වෙනවා.

එහෙත් උෂ්ණත්වය වෙනස් වන විට, ඩ්‍රිෆ්ට් වීම ඉතාම අවම කරන පරිදි සෑදූ ඔසිලේටර්ද තිබෙන බව සිහිපත් කළ යුතුය. මේවා temperature-compensated (TC) යන විශේෂන පදය සහිතව හැඳින්වෙන උපාංගවලින් සාදනු ලබනවා. එවැනි ඔසිලේටර් temperature-compensated crystal oscillator (TCXO) ලෙස හැඳින්වෙනවා. මෙවැනි උෂ්නත්ව විචලනයට අසංවේදී ඉලෙක්ට්‍රෝනික් උපාංග සාමාන්‍ය උපාංගය මෙන් කිහිප ගුණයකින් මිල අධිකය. එබැවින් එවැනි අධික මිලැති උපාංග යොදා ගෙන ඉහත කොලිටියෙන් යුතු උපකරණ සෑදීමට ගියොත් අවසානයේ උපකරණවල මිලද ඉතාම ඉහල යනු ඇති. ඒ කියන්නේ සාමාන්‍ය මිලට ඇති උපකරණවලදී SSB-SC සංඥාවලින් බුද්ධි සංඥා උකහා ගන්නා විට යම් යම් විකෘතිතා ඇතිවීම වැලැක්විය නොහැකිය.

මොන තත්වය යටතේ වුවද, එස්එස්බී රිසීවරය විසින් නිපදවන වාහකයේ සංඛ්‍යාතය ඔරිජිනල් වාහකයේ සංඛ්‍යාතයට වඩා හර්ට්ස් 10ත් 20ත් අතර ප්‍රමාණයකට වඩා වෙනස් වීම සුදුසු නොවේ.

ඉහත ගැටලුවට තවත් පිලියමක් තිබේ. එනම්, දුර්වල වාහකයක් මූර්ජිත සංඥාවේ ඉතිරි කිරීමයි. මෙවිට, වාහකය සම්පූර්ණයෙන්ම ඉවත් වන්නේ නැත. ඒ වෙනුවට අඩු වොට් ගණනක් සහිත වාහකයක් පමණක් යවනවා. මෙවිට ග්‍රාහක පරිපථයට ලැබෙනවා සත්‍ය වාහක තරංගය. SSB-SC ක්‍රමයට වඩා කුඩා වොට් ගණනක් මෙහිදී නාස්ති වන බව ඇත්තයි. එහෙත් එම නාස්තිය නොසලකා හැරිය හැකියි ඉන් ලැබෙන ප්‍රයෝජනය සැලකුවහම. මෙම දුර්වල වාහකය pilot carrier ලෙස හඳුන්වනවා. ඇත්තෙන්ම, දැන් මෙම මූර්ජන ක්‍රමය SSB with Reduced Carrier (SSB-RC) යන අලුත් නමකින්ද හැඳින්වෙනවා. මෙයම SSB with Variable Carrier ලෙසත් හැඳින්වෙනවා.

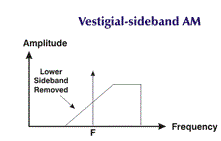
Vestigial SideBand (VSB)

වචනයෙන් කියන විට හෝ න්‍යායාත්මකව පැහැදිලි කරන විට, ඉතා පහසු යැයි සිතෙන දේවල්, ප්‍රායෝගිකව කරන විට එතරම් පහසුවෙන් ඒවා කළ නොහැකිය. ඉලෙක්ට්‍රොනික්ස්වල තිබෙන විශාලතම එක් ප්‍රශ්නයක් වන්නේ අපට අවශ්‍ය සංඛ්‍යාත පමණක් තෝරාගෙන අනවශ්‍ය සංඛ්‍යාත කපා දැමීම 100%ක් හොඳින් කළ නොහැකි වීමයි. පහත දැක්වෙන්නේ මෙම ප්‍රශ්නය රූපමය ආකාරයෙන් පෙන්වීමයි.

පරිපූර්ණ (ideal) ෆිල්ටරයකින් අවශ්‍ය හා අනවශ්‍ය සංඛ්‍යාත වෙන් කිරීම් තියුණුව (ඍජු සිරස් ඉරකින්) දැක්විය හැකියි. එවිට, එම ඉරට වම් පැත්තේ තිබෙන ඒවා තියාගෙන දකුණු පැත්තේ ඒවා කපා හැරේ යැයි කිව හැකියි. එහෙත් ප්‍රායෝගික (real/practical) ෆිල්ටරයක් පෙන්නුම් කරන්නේ සුමට වක්‍රයකිනි. ඉන් හැඟවෙන්නේ අහවල් තැන යැයි නිශ්චිතවම සීමාවක් නොමැති බවයි.

අවශ්‍ය සංඛ්‍යාත පමණක් තෝරා ගැනීම (එනම්, අනවශ්‍ය සංඛ්‍යාත පමණක් කපා දැමීම) ඉලෙක්ට්‍රොනික්ස්වල සිදු කරන්නේ filter ලෙස හැඳින්වෙන සරල පරිපථ කොටස්වලිනි. ෆිල්ටර් අපට බොහෝ පරිපථ/උපකරණ සඳහා අවශ්‍ය වේ (විශේෂයෙන්ම විදුලිසංදේශ උපකරණ සියල්ල සඳහාම). ඉහතදී මා පැවසුවා 100%ක්ම හොඳින් වැඩ කරන ෆිල්ටර් කිසිසේත් සෑදිය නොහැකි බව. ෆිල්ටරයකින් අනවශ්‍ය සංඛ්‍යාත කපා දමන විට, ඒ සමඟම අවශ්‍ය සංඛ්‍යාතද යම් ප්‍රමාණයක් කපා දැමෙනවා (හෝ දුර්වල වෙනවා). එලෙස අනවශ්‍ය සංඛ්‍යාත කපා දමන අතරම, අවශ්‍ය සංඛ්‍යාත කිසිසේත් නොකපා සිටීමට ක්‍රමයක් නැත. ඉතිං, අවශ්‍ය සංඛ්‍යාත පොඩ්ඩක්වත් කපා දැමීමට තහනම් නම්, එවිට අනිවාර්යෙන්ම අපට සිදු වෙනවා අනවශ්‍ය සංඛ්‍යාතයන් යම් ප්‍රමාණයකට ෆිල්ටරයෙන් රිංගා යෑමට ඉඩ දෙන්න.

ඉතිං මෙම ප්‍රශ්නය මතු වෙනවා SSB ක්‍රමවලදී. එහිදී එක් සයිඩ්බෑන්ඩ් එකක් කපා දමනවානෙ. එහෙත් ඉහත මා පැහැදිලි කළ ලෙස, එම කපා දැමීම 100%ක් හොඳින් සිදු කළද නොහැකිය. 100%ක් හොඳින් නොවූවත්, වඩා හොඳ (එවිට වියදමද වැඩි වනු ඇත) උපක්‍රම යෙදීමෙන් ෆිල්ටර් වීම තව තවත් හොඳ කර ගත හැකිය. එහෙත් අප සමහර අවස්ථාවලදී හොඳ උපක්‍රම යොදනවාට වඩා කරන්නේ අනවශ්‍ය සංඛ්‍යාත ප්‍රමාණයකට රිංගා යෑමට ඉඩ දී සිටීමයි (තවද, අවශ්‍ය සංඛ්‍යාත කිසිසේත් කපා දමන්නට බැහැනෙ). මෙවන් අවස්ථාවක් අපට දර්ශනය වන්නේ අපට අවශ්‍ය සයිඩ්බෑන්ඩ් එක කපා දමන්නේ නැතිව තිබෙන ගමන්ම, අනෙක් (අනවශ්‍ය) සයිඩ්බෑන්ඩ් එකෙන් යම් කොටසක් පමණක් ඉතිරිව තිබෙන්නා සේය. මෙලෙස අනවශ්‍ය සංඛ්‍යාත පරාස කොටසක් ඉතිරි වන නිසා තමයි ඊට වෙස්ටිජියල් සයිඩ්බෑන්ඩ් යන නම ලැබී තිබෙන්නේ (vestige යන ඉංග්‍රිසි වචනයෙහි තේරුම “ඉතිරි වූ කුඩා කොටසක්” යන්නයි).

VSB ක්‍රමයේදී සංඥා බෑන්ඩ්විත් එක තරමක් වැඩි වේ. ඒ කියන්නේ විදුලි බලයද තරමක් වැඩි වේ. එහෙත් දැන් පරිපථය සඳහා යොදන්නේ සරල මිල අඩු ෆිල්ටර් වේ. එය වාසියකි (වියදම අඩුවීම මෙන්ම පරිපථය නිර්මාණය කිරීමේ සංකීර්ණතාව අඩුවීම). තවද, අනවශ්‍ය “සංඥා කොටස” මඟින් අපි වැදගත් වැඩක් සිදු කරගන්නේ නැති බවද සිහිතබා ගන්න. එම කොටස තිබෙන්නේ අපට අවශ්‍ය සංඥා සම්ප්‍රේෂනය සඳහා නොවන බව සිහිතබා ගන්න (එය පරිපථ සෑදීමේදී ඇති වූ ප්‍රායෝගික ප්‍රශ්නයක් නිසා ඇති වූවක්නෙ). ටීවී සංඥා සම්ප්‍රේෂනය කරන PAL වැනි රූපවාහිනි ක්‍රමවේදය සඳහා යොදා ගන්නේ මෙම VSB ක්‍රමයයි. (ටීවී සංඥාවකදී රූප සංඥා කොටස වීඑස්බී ක්‍රමයට යවන අතර, එහි ඇති ශබ්ද සංඥා කොටස ඒ සමඟම එෆ්එම් ක්‍රමයට යැවේ.)

Independent SideBand (ISB)

ඉහත විස්තර කියවාගෙන යන අතරතුර ඔබට සිතුනේ නැද්ද සයිඩ්බෑන්ඩ් දෙකෙහි වෙනස් සංඥා දෙකක් සම්ප්‍රේෂනය කරන්නට බැරිද කියා? එසේ සයිඩ්බෑන්ඩ් දෙකෙහි වෙනස් වෙනස් සංඥා දෙකක් සම්ප්‍රේෂනය කිරීමේ ක්‍රමය තමයි ISB කියන්නේ. කෙසේ වෙතත් මෙම ක්‍රමය ක්‍රියාත්මක කිරීමේ ගැටලු ඇති අතර, එතරම් භාවිතයට ගන්නේද නැත.

ඉහත විස්තර අනුව පෙනෙනවා AM යටතේ ක්‍රම ගණනාවක්ම තිබෙන බව. ඉන් සාමාන්‍ය ඒඑම් ක්‍රමය කොතරම් අකාර්යක්ෂම වුවත් ඒඑම් රේඩියෝ චැනල් විසුරුවාලීමට භාවිතා වේ. එහෙත් ආධුනික ගුවන් විදුලියද ඇතුලුව බොහෝ ශබ්ද (කටහඬ) සම්ප්‍රේෂනය කරන විට යොදා ගන්නේ SSB-SC වේ. ඉදිරි පාඩමකදී ඒඑම් හා පසුවට කියාදෙන අනෙක් මූර්ජන ක්‍රමද යොදා ගෙන සරල පරිපථයක් නිර්මාණය කරන අයුරු බලමු.