ශ්රිත දෙකක වෙනසෙහි වර්ගඵලය සෙවීම
සාමාන්ය
නිශ්චිත අනුකලයෙන් (integration) එම ශ්රිතය
විසින් x අක්ෂය
මත සාදන වර්ගඵලය ලැබෙන බව ඔබ
දන්නවා. යම්
ශ්රිත දෙකක ප්රස්ථාර වක්ර
දෙකකින් ලැබෙන වර්ගඵලයත් එම
ශ්රිත දෙකෙහි වෙනස නිශ්චිත
අනුකලනය කිරීමෙන් ලැබෙන බවත්
මොහොතකට පෙර ඔබ දැක්කා.
එනම් පහත
ආකාරයේ ශ්රිත දෙකක වෙනසක්
නිශ්චිත අනුකලය කළ විට එම
ශ්රිත දෙකෙහි වක්ර අතර තිබෙන
වර්ගඵලය සෙවිය හැකියි.
ඉහත ශ්රිත දෙක හා ඒ අතරමැද නිර්මාණය කරන වර්ගඵලය පහත රූපයෙන් පෙනේ. ස්වායත්ත විචල්ය හරහාට හෙවත් x අක්ෂය දිගේ නිරූපණය කරන විට හා සිරස්ව හෙවත් y අක්ෂය දිගේ නිරූපණය කරන විට යන අවස්ථා දෙක සඳහාම වර්ගඵලයන් දක්වා ඇත. එනම් x විෂයෙන් අනුකලනය කරන විට පළමු රූපයේ ආකාරයෙනුත්, y විෂයෙන් අනුකලනය කරන විට දෙවන රූපයේ ආකාරයෙනුත් පෙනේවි. දෙකෙන්ම අවසානයේ ලැබෙන්නේ එකම වර්ගඵලය වේ.
උදාහරණයක්
ලෙස, y = 4x + 16 හා
y = 2x2 + 10 යන
ශ්රිත දෙක x අගය
පරාසය -1 හා
3 අතර
තුර සාදන වර්ගඵලය සොයමු.
පහත එම
ප්රස්ථාර දෙකම එකට ඇඳ ඇති
අතර, සෙවීමට
යන වර්ගඵලය තමයි කොල පාටින්
දිස්වන්නේ.
ශ්රිතය පරිභ්රමණයෙන් පරිමාව සෙවීම
මේ
ආකාරයටම සංකීර්ණ (නමුත්
නිශ්චිත රටාවක් සහිත)
හැඩතලවල
පරිමාවන් සෙවීමටද නිශ්චිත
අනුකලනය යොදා ගන්නවා.
එය සිදු කරන
පියවර කිහිපයකිනි. පළමුව
යම් ශ්රිතයක් තිබිය යුතුය.
උදාහරණයක්
ලෙස y=f(x) යන
සාධාරණ ශ්රිතයේ ප්රස්ථාර
වක්ර හැඩය පහත රූපයේ ආකාරයට
පවතී යැයි සිතමු.
දෙවනුව, එම ප්රස්ථාර වක්රය සුදුසු ප්රස්ථාර අක්ෂයක් වටා පරිභ්රමණය කළ යුතුය (පරිභ්රමණය කරනවා යනු කරකවනවා යන්නයි). උදාහරණයක් ලෙස ඉහත ප්රස්ථාර වක්රය x අක්ෂය වටා පරිභ්රමණය කළ විට පහත ආකාරයේ රූපයක් ලැබේවි.
බලන්න දැන් අපට ලැබී තිබෙන්නේ ත්රිමාන (ඝන) වස්තුවක් නේද (බුලත් හෙප්පුවක් වැනි)? ඒ කියන්නේ දැන් අපට එහි පරිමාව සෙවිය හැකියි. එහෙත් ඝනයක, සිලින්ඩරයක, ගෝලයක ආදී වස්තුවක මෙන් සරලව යම් සූත්රයකින් පරිමාව සොයන්නට බැහැ අවිධිමත් හෝ සංකීර්ණ හැඩයන් සහිත වස්තුන්වල. එහෙත්, කොතරම් සංකීර්ණ හැඩයක් සහිත වුවත්, ත්රිමාන වස්තුව ලැබුණේ ඉහත පෙන්වා දුන් පරිදි යම් ශ්රිතයක ප්රස්ථාර වක්රය කරකැවීමෙන් නම්, එවිට නිශ්චිත අනුකලනය යොදාගෙන පහසුවෙන්ම එහි පරිමාව සොයා ගත හැකිය. ත්රිමාණ වස්තුවේ පරිමාව නිර්මාණය වන්නේ කරකැවීමෙන් නිසා, පරිභ්රමණයෙන් පරිමාව (volume by revolution) සෙවීම ලෙස ඊට ව්යවහාර කෙරෙනවා. දැන් උදාහරණයක් බලමු.
y = x2 –
4x + 5 යන ශ්රිතයේ
x=1 හා
x=4 යන
පරාසය තුළ, එම
ශ්රිතය x අක්ෂය
වටා අංශක 360ක්
පරිභ්රමණය වීමෙන් සෑදෙන
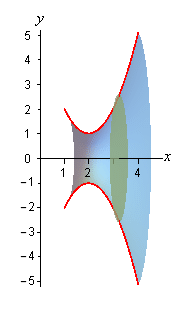
ත්රිමාන රූපයේ පරිමාව සොයමු.
පළමුව එම
ප්රස්ථාරයේ හැඩයත්,
එම හැඩය
පරිභ්රමණය කළ පසු ලැබෙන
ත්රිමාන හැඩයත් බලමු.
දැන් කොහොමද නිශ්චිත අනුකලයෙන් හරියටම පරිමාව සොයන්නේ? එය සිදු කරන්නට යන ක්රමය මෙයයි. ඉහත දකුණු පස ඇති ඝන රූපයට අවධානය යොමු කරන්න. එම ඝන රූපය පාන් ගෙඩියක් පෙති කපන්නා සේ, ඉතා සිහින් පෙතිවලට (disc) දැන් කපන්න. පෙති අනන්ත ගණනකට කැපිය යුතුය. පරිභ්රමණය නිසා හැමවිටම මෙවැනි ඝන රූපයක් පරිභ්රමණය සිදු කළ අක්ෂය වටා සමමිතික වේ. ඒ කියන්නේ එක් එක් පෙත්තක් පෙනෙන්නේ රවුම් තැටි ලෙසයි. පහත රූපවල එම තැටි අතරින් එක් තැටියක් පමණක් (කොල පාටින්) පැහැදිලිවම දර්ශනය වේ.
දැන් ඔබට පුලුවන් තැටියක මතුපිට වර්ගඵලය සොයන්න. ඒ සඳහා වෘත්තයක වර්ගඵලය සොයන සරල A = πr2 යන සූත්රය යොදන්න. මෙහි r යන අරය යනු එම පෙත්ත තිබෙන ස්ථානයේ y අගය හෙවත් ශ්රිතයයි. එය ඉහත රූපයේ දක්වා තිබෙනවා (එම අරය සහිතව තමයි x අක්ෂය වටා රවුම කරකැවෙන්නේ). ඒ කියන්නේ ඉහත රූපයේ දක්වා තිබෙන පෙත්තේ වර්ගඵලය πy2 = π(x2 – 4x + 5)2 වේ.
ඉහත
පෙත්තක ගනකම ∆x
නම්,
පෙත්තේ
පරිමාව පහසුවෙන් සෙවිය හැකියි
ඉහත ලබා ගත් වර්ගඵලය ගනකමින්
ගුණ කිරීමෙන්.
දැන්
ඔබට පැහැදිලි වෙනවානෙ මෙම
පෙති සියල්ලෙහිම පරිමාවන්
එකතු කළ විට ලැබෙන්නේ එම
සම්පූර්ණ වස්තුවේ පරිමාව
කියාත්,
එය
නිශ්චිත අනුකලයෙන් පහසුවෙන්ම
සිදු කළ හැකි බවත්.
ඒ
අනුව මෙම උදාහරණයේ පරිමාව
සොයමු.
මේ අනුව ඇත්තටම අවසානයේ ඔබට කරන්නට තිබෙන්නේ සුපුරුදු නිශ්චිත අනුකල ප්රකාශයක් සුලු කරන එක බව පේනවාද? ඔබට අමුතුවෙන් කරන්නට තිබෙන්නේ දී ඇති ශ්රිතයෙන් ඉහත විස්තර කළ ආකාරයට තුනී පෙත්තක වර්ගඵලය සොයන්නට පමණයි. ඉන්පසු එම පෙත්තේ වර්ගඵලය සොයන ශ්රිතයයි දී ඇති පරාසය තුළ අනුකල කළ යුත්තේ.
සමහරවිට
පරිභ්රමණය සිදු කරන්නේ අංශක
360ම
නොවේ.
අංශක
180ක්
හෝ වෙනත් අංශක ගණනක්ද විය
හැකියි.
එවිටත්,
ඔබ
දන්නා සාමාන්ය ගණිත දැනුම
උපයෝගි කරගෙන අවශ්ය වෙනස්
කම් සිදු කර අනුකල ප්රකාශය
සාදා ගත හැකියි.
උදාහරණයක්
ලෙස,
ඉහත
උදාහරණයේම අංශක 360
වෙනුවට
පරිභ්රමණය සිදු කරන්නේ අංශක
180 ක්
නම්,
එවිට,
පෙත්තේ
වර්ගඵලය ලෙස ගත යුත්තේ πr2
නොව
πr2/2
වේ.
අංශක
90ක්
නම් පරිභ්රමණය කරන්නේ එවිට
එය πr2/4
විය
යුතුය.
ඒ
ආදී ලෙස ඔබට එය සුදුසු පරිදි
වෙනස් කළ හැකියිනෙ.
තවත්
අවස්ථවලදී ඉහත උදාහරණයේ මෙන්
තනි ශ්රිතයක නොව,
ශ්රිත
දෙකක වෙනසක් පරිභ්රමණය
කිරීමෙන් ලැබෙන ඝන වස්තුවක
පරිමාව සොයන්නටත් වෙනවා.
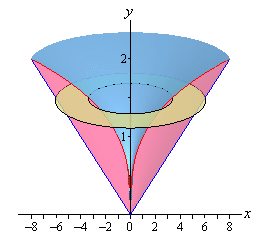
උදාහරණයක්
ලෙස පහත රූපයේ දැක්වෙනවා
ශ්රිත දෙකක් (රතු
හා නිල් වක්රවලින්).
එම
දෙක අතරමැද තිබෙන ක්ෂේත්රඵලය
y අක්ෂය
වටා පරිභ්රමණය කළ විට සෑදෙන
ඝන රූපය බලන්න.
y = x/4 හා
y = 3√x
යන
ශ්රිත දෙකයි මෙහි පවතින්නේ.
ඉහත දකුණුපස ඇති ඝන රූපයේ තද දුඹුරුපාට මැද කොටසින් කියන්නේ හිස් අවකාශයකි. එහි හැඩය සිතින් ඇඳගන්න. මෙහිදීත් අප සිදු කරන්නේ ඉහත මූලික පියවරවල්මයි. එකම වෙනස දැන් තනි වෘත්තයක් වෙනුවට වෘත්ත දෙකක වෙනසයි ගැනීමට සිදු වන්නේ.
තවද,
දැන් පරිභ්රමණය
සිදු කරන්නේ y අක්ෂය
වටා බැවින්, නිශ්චිත
අනුකලයද ඒ අනුව එම අක්ෂය දිගේ
සිදු විය යුතුය. එහෙත්
අපට ශ්රිත දෙක ලබා දී ඇත්තේ
x අක්ෂය
දිගේ පවතින ආකාරයටයි (ඒ
කියන්නේ x විචල්ය
ලෙස ඇත). දැන්
එම ශ්රිත දෙක y විචල්යය
ලෙස පවතින ශ්රිත දෙකක් බවට
පත් කරගත යුතුය. එය
ඉතාම පහසුය (x වෙනුවට
y උක්ත
වන පරිදි එම ගණිත ප්රකාශ සකස්
කරන්න).
y = x/4 → x = 4y
y
= 3√x
→ x = y3
ඉහත රූපයේ පේනවා වෘත්ත දෙකක වෙනස ගැනීමේදී ඒවා මුදු (ring) ලෙස දිස්වන බව. දැන් අපට කරන්නට තිබෙන්නේ මෙවැනි තුනී මුදු දී ඇති පරාසය තුළ අනුකලනය කිරීමයි. පළමුව මුදුවක වර්ගඵලය සොයමු.
මුදුවක
වර්ගඵලය = පිටත
රවුමේ වර්ගඵලය - ඇතුලත
රවුවේ වර්ගඵලය
= π(4y)2
– π(y3)2
= π(16y2
- y6)
එවිට
මුදුවලින් සෑදෙන මුලු ත්රිමාන
වස්තුවේම පරිමාව සොයමු (y
= 0 සිට
y = 2 යන
පරාසය තුල).
මේ ආදී ලෙස සාමාන්ය ගණිත දැනුමත් අනුකල දැනුමත් යොදාගෙන විවිධ අවස්ථාවල පරිමාවන් සොයන අයුරු ඉගෙන ගන්න.
අවසාන වශයෙන්
අනුකලනයේ
විවිධ ස්වරූප ගණනාවක් ඔබ ඉගෙන
ගත්තා - අනිශ්චිත,
නිශ්චිත,
විෂම,
බහුවිධ,
පුනර්කෘත.
තවත් සුවිශේෂි
ආකාරවල අනුකලයන් තිබෙනවා
(විශේෂයෙන්ම
දෛශිකයන් සමග අනුකල සිදු කරන
විට). අනුකලයේ
ස්වරූපය කුමක් වුවත්,
මූලික ගණනය
කිරීමේ ක්රමයේ වෙනසක් නැති
බව මතක තබා ගන්න.
අනුකලයේ
විවිධ යෙදුම් අතිවිශාල වශයෙන්
ඇත. ඒ
ඒ යෙදුම්/විෂයන්
ඉගෙන ගෙන ඒ දැනුමත් සමග අනුකලයන්
යොදා ගන්න. ගණිත
සිද්ධාන්ත තනිවම ඉගෙන ගැනීම
තරමක අභියෝගයකි මොකද ගණිතය
යනුම විද්යාව/දැනුම
ඉදිරිපත් කරන එක්තරා විදියක
භාෂාවකි.
පළමුව
ශ්රිත ගැන හොඳ දැනුමක් ලබා
ගෙන, ඉන්පසු
සීමා හා අවකලනය ගැනත් හොඳින්
ඉගෙන ගත යුතුයි අනුකලනය ඉගෙනීමට
පෙර. මේ
පොතෙහි ඉදිරිපත් කර ඇති පිළිවෙලට
ක්රමයෙන් ඉගෙන ගන්න.
කොටස් මඟ
හරිමින් ඉදිරියට ඇති පාඩම්
කියවන්නට එපා. අනුකලනය
යනු කොහොමත් තරමක අපහසුතාවක්
ඇති කරන විෂයකි. එනිසා,
ලබා දී ඇති
උපදෙස් අනුව ඉගෙන නොගත්තොත්
සමහරවිට අනුකලනය ඉගෙන ගන්නට
යන ඔබවත් "අවකලනය"
වෙලා තමයි
අවසන් වන්නේ (අනුකලනය
ගැන තරමක් හෝ උගත් බොහෝ අයට
අනුකලනය දැක්ක ගමන් අනෙයි
අපොයි කියා කියවෙන්නේ ඒ නිසා
වෙන්නටත් පුලුවන්).
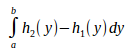













Derivatives tell us the rate.
ReplyDeleteFor areas we integrate.
Derivative, derivative,
the limit of a quotient.
A quotient, both parts going nil,
Behold, you reach a value still.
Integral, integral
the limit of the Riemann sums.
Add more and more of less and less,
The errors disappear, we guess
Calculus, calculus
United are thy branches.
Because of that eternal gem,
The Fundamental Theorem
Very beautiful... who says science is no art?
DeleteThe rate of change of a function
DeleteFluxion as known then by Newton
With his sister the Integration
The jewel of math and calculation
Wooow....
DeleteYesterday I found my first "guru dewiya" on YouTube. He said about poetry and I thought to write a poem. I stole a poem because I am not creative.
How did you become such a poet?? What is the secret? Boot ekada.? hahaa..
ගුරුතුමාගේ කවිය: https://youtu.be/kVfkQ_hv2JU 12 වන මිනිත්තුවේ සිට
Deleteඔය චැනල් එකෙත් කොහෙහරි කොමෙන්ටුවක් දාන්න...