ප්රතිරෝධක,
ධාරිත්රක
මෙන්ම ප්රේරකද පරිපූර්ණ
උපකරණයක් නොවේ.
ඒ
කියන්නේ ප්රේරකයේ ස්ට්රේ
රෙසිස්ටන්ස්,
ස්ට්රේ
කැපෑසිටන්ස් ඇත.
කොයිලය
සෑදීමට යොදාගන්නේ වයර් බැවින්
එහි ප්රතිරෝධයක් පවතිනවා.
කොයිලය
ඔතා තිබෙන ආකාරය නිසා එම කම්බි
අතර කැපෑසිටන්ස් ඇති වෙනවා
(විවිධාකාරයේ
කැපෑසිටන්ස් ඇති වන අයුරු
මීට පෙර ඉගෙන ගත්තා).
ඒ අනුව,
ප්රායෝගික/සත්ය
ඉන්ඩකටරයක ආකෘතිය පහත ආකාරයට
වේ.
ඔබට
මෙය RLC
පරිපථයක්
ලෙස පෙනෙනවා නේද?
ඔව්.
එහෙත්
මෙහි ධාරිතාව ඉතා කුඩාය.
එනිසා
අධිසංඛ්යාත සඳහා පමණයි මෙය
කරදරයක් වන්නේ (f
= 1/(2π √(LC))
අනුව).
රෙසිස්ටරයක් නොවන (ධාරිත්රකය, ප්රේරකය වැනි) උපාංගයක එම උපාංගයේ ප්රමුඛ ගතිගුණය සමග ශ්රේණිගතව පවතින ස්ට්රේ රෙසිස්ටන්ස් එක ESR (Equivalent Series Resistance) ලෙස හැඳින්වෙනවා. උදාහරණයක් ලෙස, ප්රේරකයක ප්රමුඛ ගතිගුණය ප්රේරණතාව වේ. ඉතිං මෙම ප්රේරණතාව සමග ශ්රේණිගතව පවතින ස්ට්රේ රෙසිස්ටන්ස් එක තමයි ESR ලෙස එහිදී හැඳින්වෙන්නේ. සෑම උපාංගයකම මෙම ESR පවතිනවා (මොකද සෑම උපාංගයකම ප්රතිරෝධකතා පවතින නිසා). මෙලෙසම, ප්රේරකයක් නොවන උපාංගයක එම උපාංගයේ ප්රමුඛ ගතිගුණය සමග ශ්රේණිගතව පවතින ස්ට්රේ ඉන්ඩක්ටන්ස් එක ESL (Equivalent Series Inductance) ලෙස හැඳින්වෙනවා. වයර්/පින් තිබෙන සෑම උපාංගයකම ESL පවතිනවා.
කොයිල් සෑදීම
අනෙක්
උපාංග සේම ඉන්ඩකටර්ද කඩෙන්
මිලදී ගත හැකියි.
එවිට
කලර් කෝඩ් ක්රමය හෝ ඉලක්කම්
කෝඩ් ක්රමය යන ක්රමවලින්
අගය දැක්වේ.
පහත
දැක්වෙන්නේ කලර් කෝඩ් එකයි.
(ප්රතිරෝධක
හා ධාරිත්රක හා ප්රේරක කලර්
කෝඩ් වල සියල්ලේම වර්ණවලට
හිමි අංක සමානයි නේද?)
මෙහි පළමු හා දෙවැනි තීරු දෙකේ අංක ලියා තෙවැනි තීර්වේ දැක්වෙන ඉලක්කමින් ගුණ කළ විට ලැබෙන්නේ ඉන්ඩක්ටරයේ අගය මයික්රොහෙන්රි වලිනි. හතරවැනි බෑන්ඩ් එකෙන් දැක්වෙන්නේ සහනතාවයි. හතරවැනි වර්ණ පටියක් නැති නම් 20% සහනතාවක් එහි පවතින බව සිතන්න. පහත දැක්වෙන උදාහරණය බලන්න.
එහෙත්
බොහෝවිට අපට අවශ්ය අගයන්
සහිත ඉන්ඩක්ටර් සාදා ගන්නේ
අප විසින්මයි.
ඇත්තටම
කොයිල් සාදා ගැනීම එතරම් ලොකු
වැඩක් නොවේ.
ප්රධාන
ආකාර දෙකකින් මෙම කොයිල් සාදා
ගන්නවා -
සොලිනොයිඩ්
හා ටොරොයිඩ් ලෙස.
කොයිල්
සෑදීමට ඕනෑම සන්නායක වයරයක්
භාවිතා කිරීමට හැකියි.
උදාහරණයක්
ලෙස,
යකඩ
හෝ ඇලුමිනියම් හෝ තඹ හෝ කම්බියක්
ගෙන එය පැන්සලක් වැනි දෙයක්
වටා ඔතන්න එම වටයන් (turns)
එකිනෙකට
ස්පර්ශ නොවන විදියට.
මෙය
ඉන්ඩක්ටරයකි.
මෙලෙස ගන්නා කම්බිය පරිවරණය වී තිබීම අත්යවශ්ය කොන්දේසියක් නොවේ. එහෙත් වැඩි ඉන්ඩක්ටන්ස් එකක් ලබා ගැනීමට වැඩිපුර වට ගණනක් එතීම අවශ්ය කරනවා. ඉතිං, වට ගණන වැඩි වන විට ඒවා ළඟින් ළඟින් පවතින නිසා ඒවා එකිනෙකට ස්පර්ශ (ෂෝට්) වීමේ අවදානම තිබෙනවා. එනිසා සාමාන්යයෙන් කොයිල් සෑදීමට යොදා ගන්නේ පරිවරණය කරපු කම්බි වේ. තවද, ප්රතිරෝධය අඩු තඹ ලෝහය තමයි නිතරම වාගේ යොදා ගන්නේ කොයිල් සෑදීමට. මෙම තඹ කම්බි ෂෙලැක් වැනි පරිවාරක ද්රව්යයකින් සියුම්ව පරිවරණය කර තිබෙනවා. "කොයිල් කම්බි" හෝ magnetic wire ලෙස හැඳින්වෙන්නේ මේවා තමයි.
මෙම
කොයිල් කම්බි විවිධ "මහතවල්"
(gauge – ගේජ්)
වලින්
ලබා ගත හැකිය.
මහත
වැඩි (එනම්
අරය/විශ්කම්භය
වැඩි)
කම්බි
හරහා වැඩි ධාරා ප්රමාණයක්
ගලා යා හැකියි (එතරම්
රත් නොවී).
ඒ
කියන්නේ ගලා යන ධාරාවට ගැලපෙන
පරිදියි කම්බියේ ගේජ් එක තීරණය
කරන්නේ (එය
ඕනෑම විදුලිය ගමන් කරන වයරයකට
පොදු කොන්දේසියක් කියා ඔබ
දන්නවා).
ගේජ්
එක දක්වන ප්රධාන ක්රම දෙකක්
ලොවපුරා ප්රසිද්ධයි.
එකක්
නම් එංගලන්තයේ බිහි වූ SWG
(Standard Wire Gauge) ලෙස
හැඳින්වෙන සම්මතය වන අතර,
අනෙක
ඇමෙරිකාවේ බිහි වූ AWG
(American Wire Gauge) නම්
සම්මතයයි.
මේ
දෙකෙහිම යම් කිසි අංකයකින්
වයරයේ මහත දැක්වේ.
පහත
දැක්වෙන්නේ එම සම්මත දෙකට
අදාල වගු දෙකයි.
මෙම
වගුවල ගේජ් අංකය (12,
30 වැනි
ලෙස දක්වන),
කම්බියේ
හරස්කඩ වර්ගඵලය (හෝ
එහි විශ්කම්භය හෝ අරය),
ගලා
යා හැකි උපරිම ධාරා ප්රමාණය,
මීටරයකට
(හෝ
අඩියකට හෝ මිලිමීටරයට හෝ
අඟලකට)
තිබෙන
ප්රතිරෝධි අගය ආදී වටිනා
බොහෝ විස්තර අඩංගු කළ හැකියි.
වගුවල විශ්කම්භය අඟල් (inches) හා මිලිමීටර් (mm) වලින් වෙන වෙනම දක්වා ඇත. අඟල්වලින් දී ඇති විට මිලිමීටර්වලය හා මිලිමීටර්වලින් දී ඇති විට අඟල්වලට හරවා ගැනීම ඔබටම කළ හැකි වුවත්, පහසුව පිණිසයි එලෙස නිතර භාවිතා කෙරෙන ඒකක දෙකෙන්ම එය දක්වන්නේ. ප්රතිරෝධය අඩි 1000කට කොපමණද, කිලෝමීටරයකට කොපමණද යන වගත් වෙන වෙනම සටහන් කර ඇත. යැවිය හැකි උපරිම ධාරාවද ඇත. චර්මීය ආචරණයේ බලපෑම අවසන් තීරුවෙන් දැක්වේ. ඔබ දන්නවා චර්මීය ආචරණය කියන්නේ විදුලි සංඥාවේ සංඛ්යාතය වැඩි වන විට, විදුලිය වයරයේ මතුපිටින් ගමන් කිරීමට පෙළඹීමයි. ඒ ඒ ගේජ් එක සඳහා යැවිය හැකි උපරිම සංඛ්යාතය ඉන් දැක්වේ (වැඩි විස්තර චර්මීය ආචරණය යටතේ පහත ඇත).
මෙම
වගු දෙකම තඹ කම්බි සඳහා සැකසූවකි.
තඹවල
ප්රතිරෝධකතාව 1.72
x 10-8 සලකා
ඇත.
තඹවල
ප්රතිරෝධකතාව දන්න නිසා,
ඔබට
හැකියි ඕනෑම දිගක් හා විශ්කම්භයක්
සහිත කම්බියක ප්රතිරෝධය
ගණනය කරන්නට.
ඒ සඳහා
පහත දැක්වෙන සරල සූත්රය යොදා
ගත හැකියි.
මෙහි
R
යනු
ප්රතිරෝධක අගය වන අතර,
ρ යනු
ප්රතිරෝධකතාවද,
l යනු
කම්බියේ දිගද,
A යනු
කම්බියේ හරස්කඩ වර්ගඵලයද වේ
(πr2
යන
සූත්රයෙන් මෙම වර්ගඵලය සෙවිය
හැකියි).



චර්මීය ආචරණය (skin effect) ගණනය කිරීම
ඕනෑම සන්නායකයක් දිගේ ගමන් කරන සංඥාවක් චර්මීය ආචරණයට භාජනය වේ. මෙහි ප්රතිඵලයක් වශයෙන් සන්නායකයේ මුලු හරස්කඩ ඔස්සේම ඉලෙක්ට්රෝන (ධාරාව) ගමන් නොකර, මතු පිටට වන්නට ගමන් කරයි. සංඛ්යාතය වැඩි වන විට, තව තවත් මතුපිටට ළං වී ගමන් කරයි. එවිට, ඉලෙක්ට්රෝන ගමන් නොකරන කම්බියේ මැද කොටසින් වැඩක් නැති වෙනවා. ඒ කියන්නේ වයරයේ ධාරාව ගලා යන සැබෑ හරස්කඩ (effective sectional area) කුඩා වෙනවා. චර්මීය ආචරණය නිසා, ධාරාව ගලා යන හරස්කඩේ ගැඹුර skin depth (චර්මීය ගැඹුර) ලෙස හැඳින්වෙනවා. ඇත්තටම මෙම චර්මීය ගැඹුර ලෙස පෙන්වන කොටසේ තමයි ඉතා වැඩි ප්රමාණයක් ඉලෙක්ට්රෝන ගලා යන්නේ. එහෙත් තවමත් සුලු වශයෙන් ඉලෙක්ට්රෝන කම්බියේ මැද කොටසෙත් ගමන් කරනවා. එහෙත් මැදට වන්නට වන්නට එසේ ගලන ඉලෙක්ට්රෝන ප්රමාණය ඉතා සීඝ්රයෙන් අඩු වෙනවා (ඝාතීය ශ්රිතයක් ආකාරයෙන්).සුලු වශයෙන් හෝ මැද කොටසේද ඉලෙක්ට්රෝන ගමන් කරන නිසා එම මැද කොටස්ද නොසලකා සිටිය නොහැකියි. ඊට හේතුව මෙයයි. මිලිමීටර් 10ක අරයක් සහිත කම්බියකින් යම් සංඥාවක් ගමන් කරන විට, චර්මීය ආචරණය හේතුවෙන් ඉලෙක්ට්රෝන ගලා යන්නේ මතුපිට සිට මිලිමීටර් 1ක් යටට වන ප්රදේශයෙන් යැයි කී විට, එකවර ඔබට සිතෙන්නේ එසේනම් මිලිමීටර් 9ක්ම අපතේ ගොස් ඇති බවයි. එහෙත් තත්වය මීට වඩා තරමක් වෙනස් වේ. ඊට හේතුව උඩම මිලිමීටර් 1ක කොටස (චර්මීය ගැඹුර) තුළ ඉතා විශාල ඉලෙක්ට්රෝන ගණනක් ගමන් කළද, ඊට යටින් කොටස් හරහාද තවමත් ඉලෙක්ට්රෝන ගමන් කරනවා. කොතරම් ගැඹුරට එලෙස සුලු වශයෙන් ඉලෙක්ට්රෝන ගමන් කරනවාද? දළ වශයෙන් එය චර්මීය ගැඹුර මෙන් 4 ගුණයක් යටට ගමන් කරනවා ලෙස සැලකිය හැකිය. එය, සරල රීතියක් වශයෙන් චර්මීය ගැඹුර මෙන් හතර ගුණයක් කම්බියේ මැදට වන්නට ඉලෙක්ට්රෝන ගමන් කරනවා යැයි මතක තබා ගන්න. පහත රූපයේ දැක්වෙන්නේ වයරයක හරස්කඩයි. එහි රතු වර්ණය තද වන්නට වන්නට ඉලෙක්ට්රෝන වැඩිපුර ගමන් කරන බව හඟවනවා. මතුපිට සිට මැදට (ගැඹුරට) යන විට, ගලා යන ඉලෙක්ට්රෝන (හෙවත් ධාරාව) ඝාතීය ආකාරයෙන් අඩුවන බව කොලපාට කුඩා ප්රස්ථාරයෙන්ද පෙන්වා තිබෙනවා. δ කොටසේ (වලල්ලේ) තමයි වැඩිපුරම ඉලෙක්ට්රෝන දැන් ගමන් කරන්නේ. එහෙත් d කොටස දක්වා වූ ප්රදේශයම වැදගත් කොට සලකනවා. d කොටසටත් යටින් මැදට වන්නට ඇති කොටස කිසිසේත් ප්රයෝජනයක් නැති පෙදෙසක් ලෙස සලකනවා. අවශ්ය නම්, එම කොටස සූරා ඉවත් කළ හැකියි. එවිට, කම්බිය බීම බටයක් මෙන් පෙනේවි. ඇන්ටනා බටවල මෙය සිදු කර ඇත (එනම් එහි මැද සූරා දමා ඇත).
චර්මීය ආචරණයේ ප්රතිඵලයක් වශයෙන් ප්රතිරෝධී අගය ඉහල යනවා. උදාහරණයක් ලෙස, හර්ට්ස් 100ක සංඛ්යාතයක් සහිත විදුලි සංඥාවක් සඳහා යම් කම්බියක් ඕම් 10ක ප්රතිරෝධයක් ඇති කරයි නම්, එම කම්බිය විසින්ම හර්ට්ස් 1000ක සංඛ්යාතයක් සහිත සංඥාවකට ඕම් 100ක් ලෙස දැක්විය හැකියි. එමනිසා ඇත්තටම විදුලි සංඥා ගෙන යන වයර් සඳහා ඕම් ගණනක් දැක්වීම ප්රායෝගිකද නොවේ මොකද සංඥාවේ සංඛ්යාතය අනුව එම ගණන බොහෝ සෙයින් විචලනය වේ. ඇත්තටම R =ρl/A යන සූත්රය අනුව අපට ලැබෙන්නේ සංඛ්යාතය ශූන්ය අවස්ථාවේ ප්රතිරෝධයයි. එනම්, සරල නියත ධාරාවක් සඳහා ප්රතිරෝධි අගයයි (මෙන්න මෙම ඩීසී ප්රතිරෝධය මත තමයි ඉහත කිලෝමීටරයක් හෝ අඩි 1000කට පවතින ප්රතිරෝධි අගය දක්වා තිබෙන්නේ). නියත ධාරාවක් සඳහා චර්මීය ආචරණයක් නොපවතී. චර්මීය ආචරණය ගණනය කිරීමට සරල සූත්රයක්ද ඇත. එය පහත දැක්වේ.

මෙහි δS යනු චර්මීය ආචරණය නිසා ඉලෙක්ට්රෝන කම්බියේ මතුපිටට ළං වන දුර ප්රමාණයයි (චර්මීය ගැඹුර) (මීටර් වලින්). රවුම් කම්බියක් නම් මෙම ඉවතට යෑම අරීයව සිදු වේ (එනම්, කම්බිය මැද සිට සෑම දිශාවකින්ම කම්බියේ මතුපිට දක්වා ඉවතට මෙය සිදු වේ). u යනු කම්බියේ පාරගම්යතාවයි. f යනු සංඥාවේ සංඛ්යාතයයි. p යනු කම්බියේ සන්නායකතාවයි (ඕම්-මීටර්වලින්).
ඉහත වගු දෙකෙහි සංඛ්යාත තීරු ගණනය කර තිබෙන්නේද ඉහත සූත්රය අනුවයි. එම අගයන්වල පදනම මෙසේ තර්ක කර සකස් කර ඇත. මෙලෙස සංඛ්යාතය ක්රමයෙන් වැඩි වේගෙන යන විට, ඉලෙක්ට්රෝන ක්රමයෙන් මතු පිටට ළං වෙනවා (මධ්යයෙන් ඉවත් වෙනවා). යම් අවස්ථාවක් පැමිණෙනවා ඉලෙක්ට්රෝන සම්පූර්ණයෙන්ම කම්බියේ මතුපිටටම පැමිණි. ඒ කියන්නේ ඉහත චර්මීය ආචරණ සූත්රය අනුව, (1 – δS) අගය කම්බියේ අරයට සමාන වන අවස්ථාව (එනම්, චර්මීය ගැඹුර කම්බියේ අරයට සාපේක්ෂව ඉතාම කුඩා වන අවස්ථාව). ඒ කියන්නේ ඉහත චර්මීය ආචරණ සූත්රයේ δS අගය කම්බියේ අරයට සමාන වන අවස්ථාව. මෙන්න මෙම අවස්ථාව උදාකරවන සංඛ්යාතය තමයි වගුවල දක්වා තිබෙන්නේ. එහෙත් මතක තබා ගන්න, මෙම සංඛ්යාතයෙන් කියන්නේ අදාල කම්බිය දිගේ යැවිය හැකි උපරිම සංඛ්යාතය ගැන පමණයි. සංඛ්යාතය වැඩි වන විට ක්රමයෙන් වයරයේ "සැබෑ" ඕම් ප්රමාණයද සීඝ්රයෙන් වැඩිවේ. අර උපරිම සංඛ්යාතයට ඉක්මවා යන විට, ප්රතිරෝධය (න්යායාත්මකව) අනන්තය දක්වා වැඩි වේ.
මතක
තබා ගන්න මෙම වගු දෙකෙහිම මහත
දැක්වීමට ඉලක්කම් යොදා ගත්තත්,
මේ දෙක
එකිනෙකට ගැලපෙන්නේ නැත.
උදාහරණයක්
ලෙස,
SWG 23 යන
අංකයෙන් දැක්වෙන කම්බියේ මහත
හා AWG
23 යන
අංකයෙන් දැක්වෙන කම්බියේ මහත
එකිනෙකට වෙනස්ය.
එනිසා,
කොයිල්
සෑදීමේදී ගේජ් එක දක්වා ඇත්තේ
SWG
වලින්ද
AWG
වලින්ද
යන්න ගැන සැලකිලිමත් වන්න.
තවද,
ඉහත
වගු වලංගු වන්නේ තඹ ලෝහය සඳහා
පමණයි.
එහෙත්
ඇලුමිනියම් හෝ යකඩ (හෝ
වෙනත් ලෝහ)
කම්බිද
සමහර වෙලාවට භාවිතා කෙරෙනවා.
රිදී
හැර අනෙක් සෑම ලෝහයකම ප්රතිරෝධකතාව
තඹවලට වඩා වැඩිය (මිල
අධික නිසා රිදී කම්බි යොදා
ගන්නේද නැත).
එනිසා,
යම්
ධාරාවක් යැවීමට යම් ගේජ් එකක
තඹ කම්බියක් භාවිතා කරන්නේ
නම් හා තඹ වෙනුවට වෙනත් ලෝහයක්
ආදේශ කිරීමට සිදු වුවොත්
අනිවාර්යෙන්ම එම කම්බියේ
ගේජ් එක තඹ කම්බියේ ගේජ් එකට
වඩා වැඩි විය යුතුය.
ඒ
කියන්නේ එක් එක් ලෝහ වර්ගය
අනුව ගලා යා හැකි ධාරාව වෙනස්
වේ.
ඒ
විතරක්ද නොවේ චර්මීය ආචරණයේ
බලපෑමද වෙනස් වේ (චර්මීය
ගැඹුර ගණනය කරන ඉහත සූත්රයේ
ලෝහයේ ප්රතිරෝධකතාව හා ලෝහයේ
පාරගම්යතාව ඇතුළත් වන නිසා).
ඉහත වගුවල
පදනම ප්රතිරෝධකතාව වේ.
යම්
ලෝහයක ප්රතිරෝධකතාව දන්නේ
නම්,
ඉහත
වගුවක් එම ලෝහය සඳහා ගැලපෙන
ලෙස සකසා ගැනීම පහසු වැඩකි.
කම්බියක්
හරහා ගලා යා හැකි උපරිම ධාරා
ප්රමාණය තීරණය කරන්නේ දළ
වශයෙන් එම කම්බියේ ප්රතිරෝධකතාව
හා මහත (ගේජ්
එක)
මතයි
(තවත්
සාධක කිහිපයක් ඇත).
ඉහත
වගු තඹ සඳහා සකසා ඇති නිසා,
ප්රතිරෝධකතාව
වෙනස් නොවේ.
එහෙත්
ගේජ් එක වෙනස් වේ.
එනිසයි
එක් එක් ගේජ් එකට වෙන වෙනම ගලා
යා හැකි ධාරාවන් දක්වා තිබෙන්නේ.
ඉතිං යකඩ හෝ ඇලුමිනියම් හෝ වෙනත් ලෝහ කම්බි යොදා ගන්නේ නම්, එම ලෝහයට අදාල ප්රතිරෝධකතාව පොතකින් හෝ ඉන්ටර්නෙට් එකෙන් හෝ පහසුවෙන් සොයා ගත හැකියි. ඉන්පසු ඉහත වගුවකට සමාන වගුවක් සකස් කරගත හැකියි.
එහිදී ගේජ් තීරුව හා විශ්කම්භ තීරුව වෙනස් නොකර එලෙසම තබන්න.
(කිලෝමීටරයට හා අඩි 1000 ක් සඳහා වූ) ප්රතිරෝධ අගය පෙන්වන තීරු ඉහත R= pl/A සූත්රය අනුව ගණනය කර පුරවන්න (ඒ ඒ ගේජ් එක සඳහා).
ඉන්පසු එක් එක් ගේජ් එකක් සඳහා තඹ කම්බියේ ප්රතිරෝධකතාව හා අනෙක් (ඇලුමිනියම් හෝ වෙනත්) කම්බියේ එම ගේජ් එකේම ප්රතිරෝධකතාව අතර අනුපාතය ගන්න; දැන් එම අනුපාතයට අනුව ධාරාව සොයන්න (එනම්, තඹවල ප්රතිරෝධකතාව අනෙක් ලෝහයේ ප්රතිරෝධකතාවෙන් බෙදා, එසේ ලැබෙන අගය යම් තඹ ගේජ් එකකට දැරිය හැකි උපරිම ධාරාවෙන් ගුණ කරන්න; එවිට ලැබෙන්නේ අදාල ලෝහයේ එම ගේජ් එකට දැරිය හැකි උපරිම ධාරාවයි). මෙලෙස සෑම ගේජ් එකක් සඳහාම එය සිදු කළ හැකියි. එවිට උපරිම ධාරා තීරුවත් සම්පූර්ණ වේ.
දැන් පිරවීමට ඇත්තේ චර්මීය ආචරණ තීරුවයි. එයත් ඉහත චර්මීය ආචරණය පිළිබඳ සූත්රය මඟින් ගණනය කළ හැකියි. මේ ආකාරයට ඇලුමිනියම්, යකඩ ආදී කම්බි සඳහාද ඉහත වගු සකසා ගත හැකියි. ඒ හැරත් සරල ගණිතය යොදා ගෙන ඕනෑම ගේජ් එකක ඕනෑම දිගක ඕනෑම ලෝහයක (එහි ප්රතිරෝධකතාව දන්නවා නම්) කම්බියක් සඳහා ඉහත ගලා යා හැකි උපරිම ධාරාව, ප්රතිරෝධ අගය, චර්මීය ගැඹුර ආදී අගයන් ගණනය කළ හැකියි. මෙම ගණනය කිරීමෙන් ලැබෙන වගු ඉතාම දළ අගයන් බව මතක තබා ගන්න.
ඉතිං යකඩ හෝ ඇලුමිනියම් හෝ වෙනත් ලෝහ කම්බි යොදා ගන්නේ නම්, එම ලෝහයට අදාල ප්රතිරෝධකතාව පොතකින් හෝ ඉන්ටර්නෙට් එකෙන් හෝ පහසුවෙන් සොයා ගත හැකියි. ඉන්පසු ඉහත වගුවකට සමාන වගුවක් සකස් කරගත හැකියි.
එහිදී ගේජ් තීරුව හා විශ්කම්භ තීරුව වෙනස් නොකර එලෙසම තබන්න.
(කිලෝමීටරයට හා අඩි 1000 ක් සඳහා වූ) ප්රතිරෝධ අගය පෙන්වන තීරු ඉහත R= pl/A සූත්රය අනුව ගණනය කර පුරවන්න (ඒ ඒ ගේජ් එක සඳහා).
ඉන්පසු එක් එක් ගේජ් එකක් සඳහා තඹ කම්බියේ ප්රතිරෝධකතාව හා අනෙක් (ඇලුමිනියම් හෝ වෙනත්) කම්බියේ එම ගේජ් එකේම ප්රතිරෝධකතාව අතර අනුපාතය ගන්න; දැන් එම අනුපාතයට අනුව ධාරාව සොයන්න (එනම්, තඹවල ප්රතිරෝධකතාව අනෙක් ලෝහයේ ප්රතිරෝධකතාවෙන් බෙදා, එසේ ලැබෙන අගය යම් තඹ ගේජ් එකකට දැරිය හැකි උපරිම ධාරාවෙන් ගුණ කරන්න; එවිට ලැබෙන්නේ අදාල ලෝහයේ එම ගේජ් එකට දැරිය හැකි උපරිම ධාරාවයි). මෙලෙස සෑම ගේජ් එකක් සඳහාම එය සිදු කළ හැකියි. එවිට උපරිම ධාරා තීරුවත් සම්පූර්ණ වේ.
දැන් පිරවීමට ඇත්තේ චර්මීය ආචරණ තීරුවයි. එයත් ඉහත චර්මීය ආචරණය පිළිබඳ සූත්රය මඟින් ගණනය කළ හැකියි. මේ ආකාරයට ඇලුමිනියම්, යකඩ ආදී කම්බි සඳහාද ඉහත වගු සකසා ගත හැකියි. ඒ හැරත් සරල ගණිතය යොදා ගෙන ඕනෑම ගේජ් එකක ඕනෑම දිගක ඕනෑම ලෝහයක (එහි ප්රතිරෝධකතාව දන්නවා නම්) කම්බියක් සඳහා ඉහත ගලා යා හැකි උපරිම ධාරාව, ප්රතිරෝධ අගය, චර්මීය ගැඹුර ආදී අගයන් ගණනය කළ හැකියි. මෙම ගණනය කිරීමෙන් ලැබෙන වගු ඉතාම දළ අගයන් බව මතක තබා ගන්න.
සටහන
නිතර භාවිතා වෙන සන්නායක කිහිපයක ප්රතිරෝධකතා පහත දැක්වේ. Ohm meter යන සම්මත ඒකකයෙන් ඒ සියල්ල මනිනු ලැබේ.
නිතර භාවිතා වෙන සන්නායක කිහිපයක ප්රතිරෝධකතා පහත දැක්වේ. Ohm meter යන සම්මත ඒකකයෙන් ඒ සියල්ල මනිනු ලැබේ.
Silver
(රිදී)
- 1.59x10-8 Copper (තඹ)
– 1.72x10-8
Aluminium – 2.8x10-8 Gold (රත්තරං) - 2.4x10-8
Iron (යකඩ) – 1x10-7 Zinc – 5.5x10-8
Tin – 1.1x10-7 Lead (ඊයම්) - 1.7x10-7
Nickel – 7x10-7 Tungsten – 5.6x10-8
Nichrome – 1x10-6 Carbon (graphite) – 1x10-5
Aluminium – 2.8x10-8 Gold (රත්තරං) - 2.4x10-8
Iron (යකඩ) – 1x10-7 Zinc – 5.5x10-8
Tin – 1.1x10-7 Lead (ඊයම්) - 1.7x10-7
Nickel – 7x10-7 Tungsten – 5.6x10-8
Nichrome – 1x10-6 Carbon (graphite) – 1x10-5
උදාහරණයක්
ලෙස ඇලුමිනියම් ලෝහය සලකමු.
ඇලුමිනියම්
හා තඹ දෙකෙහි සන්නායකතා දෙකෙහි
අනුපාතය (1.72x10-8)/(2.8x10-8)
= 0.61 වේ.
දැන්
ඉහත තඹ සඳහා වූ වගුවක ධාරාව
පෙන්වන තීරය මෙම 0.61
යන
අගයෙන් ගුණ කරගෙන යන්න.
ඇත්තෙන්ම
මෙලෙස ගණනය කිරීමෙන් ඔබට
ලැබෙන්නේ දළ අගයන් පමණි.
(වයරයක්
තුළින් ගලා යා හැකි ධාරාව
තීරණය කිරීමේදී තවත් සාධක
පවතින බැවින්,
ඒ
කිසිවක් මෙහිදී සලකා නොමැත.)
ඉහත
පෙන්වූ පරිදි ඇලුමිනියම්වල
සන්නායකතාව තඹවල සන්නායකතාවෙන්
61%කි
(0.61).
එනිසා,
AWG වගුවෙන්
යම් තඹ කම්බි ගේජ් එකක් ගත්
විට,
එම තඹ
කම්බිය වෙනුවට ඇලුමිනියම්
කම්බියක් ආදේශ කිරීමට අවශ්යයි
නම්,
තඹ
කම්බියේ අංකයට 2ක්
අඩු ගේජ් එක සහිත ඇලුමිනියම්
කම්බියක් යොදා ගත හැකියි.
උදාහරණයක්
ලෙස,
AWG 20 ගේජ්
එක සහිත තඹ කම්බිය වෙනුවට AWG
18 සහිත
ඇලුමිනියම් කම්බියක් ඒ සඳහා
ආදේශ කළ හැකියි.
මෙය
සරල රීතියකි (rule
of thumb).
අපට
අවශ්ය හෙන්රි ප්රමාණය ලැබෙන
හා අවශ්ය ධාරා ප්රමාණය යැවිය
හැකි ප්රේරකයක් සාදා ගන්නේ
කෙලෙසදැයි දැන් බලමු.
සරලව
ගතහොත් ඔබට අවශ්ය ධාරා ප්රමාණය
යැවීමට කරන්න තියෙන්නේ ඉහත
වගුවක් ආශ්රයෙන් කොයිලයේ
ගේජ් එක තෝරා ගැනීම පමණයි.
එහෙත්
හෙන්රි ප්රමාණය සැකසීම එතරම
සරල නැත.
එය ඔතන
වට ප්රමාණය,
කොයිලයේ
දිග ආදී සාධක තුන හතරක් මත
තීරණය වන්නක්.
ඇත්තටම
ආකාර කිහිපයකින්ම කොයිල්
සෑදිය හැකි නිසා,
ඒ සෑම
එකකටම පොදු සූත්රයක් දිය
නොහැකි වුවත්,
මූලික
සිද්ධාන්ත දන්නවා නම් දළ
වශයෙන් එ් එක් එක් ආකාර සඳහා
සූත්ර සාදා ගත හැකියි.
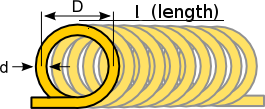
පහත
දැක්වෙන්නේ බහුලවම භාවිතා
වන සොලිනොයිඩ් වර්ගයේ කොයිලයක්
සඳහා සූත්රයක් නිර්මාණය කර
ගන්නා ආකාරයයි.
චුම්භක ස්රාවය හා ස්රාව ඝනත්වය
චුම්භක
හෝ විද්යුත් චුම්භකයක් අවට
චුම්භක ක්ෂේත්රයක් ඇතිවන
බව ඔබ දන්නවා.
එම
ක්ෂේත්රය "චුම්භක
ස්රාවය"
(magnetic flux) යන
නමින් හැඳින් වෙනවා.
(චුම්භක
ස්රාවය (ϕ)
වෙබර්
(Weber)
යන
ඒකකයෙන් මැනේ.
පැරණි
ක්රමයේදී මැක්ස්වෙල් (Mx)
යන
ඒකකයෙන්ද එය මැන්නා.)
1
Wb = 108 Mx
යම්
ප්රදේශයක් පුරා පැතිර පවතින
චුම්භක ස්රාවය එම ප්රදේශයේ
ක්ෂේත්රඵලයෙන් බෙදීමෙන්
"ඒකක
ක්ෂේත්රඵලයකට චුම්භක ස්රාවය"
හෙවත්
චුම්භක ස්රාව ඝනත්වය (flux
density) ලැබේ
(ඉහත
රූපයේ සිලින්ඩර් හැඩයේ ඉහළ
හරස්කඩ ක්ෂේත්රඵලයට ලම්භකව
B
ස්රාව
ඝනත්වය පිහිටන අයුරු බලන්න).
පහත
රූපයද බලන්න.
ස්රාවය
(එනම්
ස්රාව රේඛා)
තලයට
ලම්භක නොවී යම් ϴ
කෝණයකින්
ඇලවී නම් පවතින්නේ එවිට පෙන්වා
දී ඇති පරිදි කොස්(ϴ)
සූත්රයට
ඇතුලු වේ (ගණිතයේ
ත්රිකෝණමිතික නියමයන් අනුව)

ඇත්තටම
චුම්භක සමග ගනුදෙනු කරන හැමවිටම
පාහේ අප යොදා ගන්නේ මෙයයි.
එය B
යන
අකුරින් සංඛේතවත් කරන අතර,
මනින
ඒකකය වන්නේ ටෙස්ලා (Tesla
– T) හෝ
"වර්ග
මීටරයට වෙබර්"
(Wb/m2) වේ
(පැරණි
මිනුම් ක්රම අනුව මෙය ගවුස්
(Gauss)
(G) වලින්ද
මනිනු ලැබේ).
1
T = 104 G
B
ගණනය
කිරීමේදී ක්ෂේත්රඵලයට ලම්භකව
පවතින චුම්භක ස්රාවයයි ගණන්
ගන්නේ.
පොලොවේද
යම් චුම්භක ක්ෂ්රෙතයක් පවතින
බව ඔබ දන්නවා (මාලිමා
ක්රියා කරන්නේ මෙම චුම්භක
ක්ෂේත්රයට සංවේදීවයි).
දළ
වශයෙන් පොලොවේ චුම්භක ක්ෂේත්රයේ
ස්රාව ඝනත්වය ගවුස් 0.5ක්
පමණය.
චුම්භකයක H අගය (චුම්භකතාව)
තවද,
චුම්භක
ධ්රැවයක (එනම්,
චුම්භකයක)
පවතින
"චුම්භකතාව"
ගැනද
අපට අදහසක් තිබිය යුතුය.
ආරෝපණයක
ප්රබලතාව අප කූලෝම්වලින්
මැන්නා.
එලෙසම
චුම්භකයක ප්රබලතාව (මා
එය චුම්භකතාව/චුම්භකත්වය
යන නමින් හඳුන්වන්නට කැමතියි)
මනින්නේ
"මීටරයට
ඇම්පියර් වට"
යන
ඒකකයෙනි.
මෙම
චුම්භකත්වය H
අකුරින්
සංඛේතවත් කෙරේ (ඉංග්රිසියෙන්
මෙය magnetic
field strength, magnetizing force, H-field ආදී
වචනවලිස් හැඳින්වෙනවා).
මෙම
ඒකකය මෙලෙස නිර්වචනය කිරීමට
හේතුව කෙටියෙන් බලමු (හරිම
සරල තර්කයක් එතැන තිබෙන්නේ).
සාමාන්ය
කාන්දම් හා විද්යුත් චුම්භක
යන දෙකෙහිම පවතින්නේ එකම
චුම්භකතාවයි.
වෙනස
නම්,
සාමාන්ය
කාන්දම්වල එම කාන්දම් ගුණය
පවතින්නට පිටතින් විදුලි
ධාරාවක් අවශ්ය නොකිරීමයි;
විද්යුත්
චුම්භකයක චුම්භකතාවට හේතුව
විදුලි ධාරාවකි.
සිතන්න
යම් ප්රබලතාවක් සහිත සාමාන්ය
කාන්දම් කැබැල්ලක් තිබෙනවා
කියා.
එහි
ප්රබලතාව අපට චුම්භකත්වය
මනින උපකරණයක් ඇසුරින් මැනිය
හැකියි.
දැන්
එම ප්රබලතාවම සහිත විද්යුත්
චුම්භකයක්ද ගන්න.
මෙම
ප්රබලතාව ඇති කිරීමට අවශ්ය
කරන ධාරාව ඔබට මැනගත හැකියි.
ඒ
කියන්නේ දැන් මෙම චුම්භක දෙක
සමානයි;
එවිට
විද්යුත් චුම්භකයේ ධාරාව
ඇසුරින් මේ දෙවර්ගයේම චුම්භක
ගැන අධ්යනය කිරීමට අපට හැකියි
නේද?
(මෙය
ආකෘතියකි.)
එය පහත
ආකාරයට දැක්විය හැකියි.
සටහන
ඉහත සිදු කළ ක්රියාව (එසේත් නැතිනම් ඉහත ආකාරයේ ආකෘතියක් ගොඩ නැඟීම) විද්යා හා තාක්ෂණ ලෝකයේ නිතර සිදු වන්නකි. යම් කිසි ගුණයක් ඔබට මැනගත හැකියි තවත් දෙයක් ආශ්රයෙන්. උදාහරණයක් ලෙස ඔබ සතුව බිස්කට් පෙට්ටියක් ඇතැයි සිතන්න. ඔබට පුලුවන් එහි පරිමාව හරියටම ගණනය කරන්න එහි දිග, පළල, උස යන තුන එකට ගුණ කිරීමෙන්. දැන් ඔබ සතුව අවිධිමත් හැඩයක් සහිත විශාල කලු ගල් කැබැල්ලක පරිමාව සෙවීමට කිව්වොත් එය කළ හැකිද ඉහත ආකාරයට දිග, පළල, උස එකිනෙකට ගුණ කිරීමෙන්? බැහැ නේද?
ඉහත සිදු කළ ක්රියාව (එසේත් නැතිනම් ඉහත ආකාරයේ ආකෘතියක් ගොඩ නැඟීම) විද්යා හා තාක්ෂණ ලෝකයේ නිතර සිදු වන්නකි. යම් කිසි ගුණයක් ඔබට මැනගත හැකියි තවත් දෙයක් ආශ්රයෙන්. උදාහරණයක් ලෙස ඔබ සතුව බිස්කට් පෙට්ටියක් ඇතැයි සිතන්න. ඔබට පුලුවන් එහි පරිමාව හරියටම ගණනය කරන්න එහි දිග, පළල, උස යන තුන එකට ගුණ කිරීමෙන්. දැන් ඔබ සතුව අවිධිමත් හැඩයක් සහිත විශාල කලු ගල් කැබැල්ලක පරිමාව සෙවීමට කිව්වොත් එය කළ හැකිද ඉහත ආකාරයට දිග, පළල, උස එකිනෙකට ගුණ කිරීමෙන්? බැහැ නේද?
එහෙත්
එම අවිධිමත් ගල් කැබැල්ලේ
පරිමාව පහසුවෙන්ම සොයා ගත
හැකියි එම ගල් කැබැල්ල "කට
කැපෙන්නට"
වතුර
පිරවූ භාජනයක් තුළට දමා,
එවිට
ඉවත් වන (පිටාර
ගලන)
වතුර
ප්රමාණය මැන ගැනීමෙන්.
ගලෙහි
පරිමාව වන්නේ එලෙස පිටාර ගැලූ
වතුර ප්රමාණයේ පරිමාවයි.
(මෙය
ආකිමිඩිස් විසින් පළමු වරට
පෙන්වා දුන් නියමයක්.)
ඒ
කියන්නේ ඔබ ගලෙහි පරිමාව
මැන්නේ එය ඍජුවම මැන බලා ගණනය
කර නොව,
වතුර
ආශ්රයෙන්ය.
මෙය
වක්ර ක්රමයක්.
එහෙත්
අපට අවශ්ය දේ සිදු වූවා.
ඉහත
කාන්දම් ගැනද කීමට තිබෙන්නේ
එයමයි.
සාමාන්ය
කාන්දම් කෑලිවල ප්රබලතාව
උපකරණ මඟින් මැනිය හැකි වුවත්,
එය
ගණිත ක්රමයකින් මැන ගණනය
කිරීමට බැරිය.
එහෙත්
විද්යුත් චුම්භක එසේ නොවේ.
කොයිලය
හරහා ගලන ධාරාව දන්නේ නම් අපට
චුම්භකයේ ප්රබලත්වය ගණනය
කළ හැකියි (එනම්,
අර්ථ
කථනය කළ හැකියි).
දෙකම
අවසාන වශයෙන් චුම්භක නිසා,
ධාරාව
ආශ්රයෙන් වක්රව කාන්දම්
කෑලිවලද ප්රබලත්වය කිව හැකි
බවයි මා පෙන්වා දීමට උත්සහ
කළේ.
ඉහත
පෙන්වා දුන් පරිදි විදුලියේ
ප්රමුඛ ඒකකය වන ධාරාවමයි
චුම්භකවලදිත් ප්රමුඛ වන්නේ.
ඒ
වගේමයි වට ගණන වැඩි වන විටද
චුම්භකත්වය වැඩි වේ.
සිතන්න
දිගු කම්බියක් හරහා ධාරාවක්
ගමන් කරනවා කියා.
එවිට
යම් චුම්භක ප්රබලතාවක් එහි
ඇති වෙනවානෙ ඉහත කියූ ආකාරයට.
දැන්
එම කම්බියම වට කිහිපයක් එන
පරිදි නැවූ විට (කොයිලයක්
ආකාරයට)
එම වට
ප්රමාණයට සමානුපාතිකව චුම්භකය
ප්රබල වේ.
එනිසා
තමයි ධාරාව පමණක් නොගෙන ධාරාව
(I)
හා වට
ගණන (N)
යන
දෙකම සලකන්නට සිදු වන්නේ.
ඒ අනුව
ඉහත පෙන්වූ සරල සම්බන්ධතාව
පහත ආකාරයට තවත් නිවැරදි වේ.
මේ
ගැන තවත් විමසා බලමු.
තනි
පොටක් හෝ පොටවල් N
සංඛ්යාවකින්
යුතු සන්නායක දිගේ දැන් ධාරාවක්
ගලා යනවා.
ඉන්
චුම්භක කේෂ්ත්රයක් වලලු
ආකාරයෙන් හටගන්නවානෙ.
NI යනු
සමස්ථ කම්බිය හෝ කම්බි සෙට්
එක පුරාම මෙලෙස පවතින චුම්භක
ක්ෂේත්රය පිළිබඳ රාශියකි.
දැන්
එම කම්බිය හෝ කම්බි සෙට් එකේ
දිග දෙගුණයකින් දික් කළා යැයි
සිතන්න.
මෙවිට
ඔබට එකවරම සිතේවි එවිට,
NI ද
දෙගුණයක් විය යුතු බව මොකද
දැන් අමතරව තවත් දිගක් ඔස්සේ
චුම්භක ක්ෂේත්රයක් පවතින
නිසා.
එහෙත්
දිග දෙගුණකයකින් වැඩි කළ විට
කම්බිවල ප්රතිරෝධයද දෙගුණයකින්
වැඩි වුණා.
එවිට
V=IR
සූත්රය
අනුව ධාරාව භාගයකින් (½)
අඩු
වුණා.
ඒ
කියන්නේ දැන් කම්බිය හෝ කම්බි
සෙට් එක දිගේම පවතින චුම්භක
ක්ෂේත්රය මුල් තිබූ ක්ෂේත්රයෙන්
හරි අඩකි.
ඉතිං
දෙගුණයක් වීම නිසා එම අමතර
කොටසෙහි රඳන චුම්භක ක්ෂේත්රය
හිලව් වෙනවා චුම්භක ක්ෂේත්රය
අඩකින් අඩු වීම නිසා.
මින්
පැහැදිලි වෙනවා කම්බියේ දිග
NI
ට වැදගත්
නැති බව.
එය
හරියට පාන් ගෙඩියකට පෙති
කොතරම් ප්රමාණයක් කැපුවත්,
ඒ සියලු
පෙති අවසානයේ මුල් පාන් ගෙඩියට
වඩා වැඩි වන්නේ නැහැ වගේය.
දැන්
ඔබට සිතිය හැකියි කම්බිය හෝ
කම්බි සෙට් එක මැදි කොට ගෙන
ඒ වටා සිලින්ඩරයක් ආකාරයට
චුම්භක ක්ෂේත්රයක් පවතිනවා.
දැන්
එම කම්බිය හෝ කම්බි සෙට් එක
අසල ඕනෑම ලක්ෂ්යයක් සැලකූ
විට එතැන තිබෙන චුම්භකත්වයේ
ප්රබලතාව තමයි H
කියන්නේ.
ඒ
කියන්නේ ඉහත සම්බන්ධතාව
තවදුරටත් පහත ආකාරයට සකස් කළ
හැකියි.
මෙම
චුම්භකත්වය ස්රාව ඝනත්වය
වගේම වැදගත් රාශියකි.
ඇත්තටම
මේ දෙක අතර පහත ආකාරයේ සම්බන්ධතාවක්ද
පවතනිවා.
මෙම
සම්බන්ධතාව වටහගත යුත්තේ
මෙලෙසයි.
චුම්භකය
(හෝ
විද්යුත් චුම්භකය)
තුළ
එම චුම්භක ගුණය ඉස්මතු කරවන
කෙනා තමයි H.
එහෙත්
චුම්භකය සෑදී ඇති ඒ ඒ ද්රව්ය
අනුව,
එම
චුම්භකය විසින් ඇති කරන චුම්භක
ස්රාව ඝනත්වය තීරණය වෙනවා.
එකම
H
අගය
සහිත එක් ද්රව්යයක් විසින්
ඇති කරන ස්රාව ඝනත්වය නොවේ
තවත් ද්රව්යයක් ඇති කරන්නේ.
B
= uH
මෙහි
u
යන්න
පාරගම්යතාව (permeability)
ලෙස
හැඳින්වේ.
විදුලියේදී
මතකද පාරවේද්යතාව යනුවෙන්
දෙයක් හමු වූවා?
විදුලි
ක්ෂේත්රයක් පැතිරීමට ඇති
පහසුතාව තමයි ඉන් හැඟවූයේ.
එලෙසම
චුම්භක ක්ෂේත්රයක් පැතිරීමට
ඇති පහසුතාව තමයි පාරගම්යතාව
යනුවෙන් හැඳින්වෙන්නේ.
පාරගම්යතාව
වැඩි මාධ්යයක් තුළ චුම්භක
ක්ෂේත්රය පහසුවෙන්/ශක්තිමත්ව
පැතිරෙනවා.
රිකත්කයේ
පාරගමග්යතාව නියතයක් වන අතර
එය 4π
x 10-7 යන
අගය සහිතයි (uO
යන
සංඛේතය ඊට යෙදේ).
දළ
වශයෙන් වාතයේ (වායුගෝලයේ)
පාරගම්යතාවද
එයමයි.
එහෙත්
විවිධ මාධ්යවල පවතින්නේ
විවිධ පාරගම්යතා අගයන්ය.
පාරවේද්යතාව
ගැන කතා කිරීමේදී සාපේක්ෂ
පාරවේද්යතාව අර්ථ දැක්වූ
විදියටම,
මෙහිදීද
සාපේක්ෂ පාරගම්යතාවක්
(relative
permeability, ur) අර්ථ
දැක්විය හැකියි.
එනම්,
යම්
මාධ්යයක සාපේක්ෂ පාරගම්යතාව
=
(එම
මාධ්යයේ පාරගම්යතාව)/(රික්තයේ
පාරගම්යතාව)
(
ur = u/u0)
සාපේක්ෂ
පාරගම්යතාවෙන් 1ක්
අඩු කළ විට ලැබෙන රාශියට
magnetic
susceptibility යන
නම ව්යවහාර කෙරෙනවා.
එය χ
යන
ග්රීක අකුරින් සංඛේතවත්
කෙරෙනවා.
χ
= ur
- 1
චුම්භකගාමක
බලය (magnetomotive
force – mmf) යනුවෙන්ද
වචනයක් අපට හමු වෙනවා.
එය
හරියට විදුලියේදී හමුවන
විද්යුත්ගාමක බලය (electromotive
force – emf) වගේම
රාශියක්.
ඔව්,
විදුලියේදී
emf
වලට
හිමි ස්ථානය තමයි චුම්භකවලදී
mmf
ට හිමි
වන්නේ.
චුම්භකත්වය
චුම්භකයේ දිගින් වැඩි කිරීමෙන්
mmf
අගය
ලැබේ.
mmf
= Hl (H - චුම්භකතාව,
l (එල්
අකුර)
- චුම්භකයේ
දිග)
H
= NI/l නිසා,
ඉහත
සූත්රය පහත ආකාරයටද ලිවිය
හැකියි නේද?
mmf
= Hl (එල්)
= NI (අයි)
Magnetic circuit ආකෘතිය
යම්
සන්නායකයක අග්ර දෙක අතර යම්
විද්යුත්ගාමක බලයක් ඇති
විට,
එම
සන්නායකය දිගේ විදුලි ධාරාවක්
(ඉලෙක්ට්රෝන)
ගමන්
කරනවා.
එලෙසම,
යම්
(කාන්දම්)
ද්රව්යයක්
දෙපස චුම්භකගාමක බලයක් ඇති
විට,
ඒ හරහා
චුම්භක ස්රාවයක් ගමන් කරනවා.
විද්යුත්ගාමක
බලය නිසා ගමන් කරන ධාරාවට එම
මාධ්යය විසින් ප්රතිරෝධකතාවක්
දක්වනවා (එනම්,
ධාරාව
ගැලීමට බාධාවක්).
එලෙසම,
චුම්භකගාමක
බලය නිසා චුම්භක ස්රාවයක්
ගමන් කරන විට,
මාධ්යය
විසින් ඊට "චුම්භක
ප්රතිරෝධකතාවක්"
(reluctance – R) දක්වනවා.
රිලක්ටන්ස්
හි පරස්පරය (1/R)
හැඳින්වෙන්නේ
permeance
(P) ලෙසයි.
මේ
අනුව,
ඔබට
පැහැදිලිවම පෙනෙනවා විදුලිය
හා චුම්භක අතර එකිනෙකට අනුගතව
පවතින සංකල්ප/සූත්ර
පවතින බව.
ඒ
කියන්නේ විදුලියේදී ධාරාවට
හිමි තැන චුම්භකවලදී චුම්භක
ස්රාවයටද,
ප්රතිරෝධය
හිමි තැන රිලක්ටන්ස්වලටද
හිමි වෙනවා.
එම
සම්බන්ධතාව සූත්රයක් ලෙස
පහත ආකාරයට ලිවිය හැකියි.
මෙය
විදුලියේදී ඔබ ඉගෙන ගත් ඕම්
නියමයට අනුරූප සූත්රයක්
නේද?
මෙම
සූත්රය Hopkinson's
Law යන
නමින් හැඳින්වෙනවා.
mmf
= (Magnetic flux)(Reluctance) mmf = ϕR
ඕම්
නියමය පිළිපදින විට ඇති වන්නේ
ඉලෙක්ට්රික් සර්කිට් එකකි.
එලෙසම
හොප්කින්සන් නියමය පිළිපදින
විට ඇති වන්නේ මැග්නටික්
සර්කිට් (චුම්භක
පරිපථයක්)
ය.
මතක
තබා ගන්න චුම්භක පරිපථය යනු
හුදෙක්ම පහසුවෙන් ගණන් සෑදීමට
(විශ්ලේෂණ
කටයුතුවලට)
යොදා
ගැනීමට ගොඩ නඟා ගත් ආකෘතියක්
පමණයි.
ඇත්තටම
විදුලිය හා චුම්භක සූත්ර
අතර තිබෙන සමානකම් තවදුරටත්
ගමන් කරනවා.
ඔබ
දන්නවා යම් ප්රතිරෝධි
ද්රව්යයක ප්රතිරෝධය මැනීමට
R
=pl/A යන
සූත්රය යොදා ගන්නා බව (p
යනු
ද්රව්යයේ ප්රතිරෝධකතාවයි).
මෙම
සූත්රයම R
= l/σA ලෙසටත්
ලියනවා (
σ යනු
ද්රව්යයේ සන්නායකතාවයි).
එක
සූත්රයක ප්රතිරෝධකතාවද
අනෙක් සූත්රයට සන්නායකතාවද
යොදාගෙන තිබෙනවා (σ
= 1/p). මේ
ආකාරයටම චුම්භකයක රිලක්ටන්ස්
එකද ලිවිය හැකියි.
එය
පහත ආකාරයට සාධනය කළ හැකියි.
විදුලියේදී
සන්නායකතාව යනු විදුලි ධාරාව
ගමන් කිරීමට ඇති පහසුතාව වන
අතර,
චුම්භකවලදී
පාරගම්යතාව යනු චුම්භක
ස්රාවය ගමන් කිරීමට ඇති
පහසුතාව වේ.

හරි
ඔබ මෙතෙක් උගත් කරුණු අනුව
කොයිලයක අගය තීරණය කරන අයුරු
බලමු.
මීට
පෙර උගත් ෆැරඩේ නියමය හා අනෙක්
කරුණු අනුව පහත ආකාරයට සූත්රයක්
සාධනය කළ හැකියි,

ඉහත
අවසාන සූත්රය තමයි අපට වැදගත්
වන්නේ.
මෙහි
දිග (l)
හා
ක්ෂේත්රඵලය (A)
පිළිවෙලින්
මීටර් හා වර්ගමීටර්වලින්
තැබිය යුතුය.
තවද,
මෙම
සූත්රය අදාල වන්නේ හිඩැසක්
නැතිව කම්බි වටයන් ළඟින් ළඟින්
ඔතා ඇති කොයිල්වලටයි (කම්බි
පොටවල් අතරේ හිඩැස් තබන්නෙ
නැතිව).
තවද,
කම්බි
එක උඩ එක එතිය නොහැකියි.
මෙවැනි
කොයිල් "තනි
ස්ථරයේ කොයිල්"
(single-layer coil) ලෙස
හැඳින්වේ.
ඉහත
සූත්රය අනුව වට ඈතින් ඈතට
එතුවොත් (ඉන්
l
වැඩි
වන බැවින්)
ප්රේරණතාව
අඩු වේ.
මෙයින්
පෙනෙනවා කොයිලයේ පොටවල් එහා
මෙහා කිරීමෙන් ප්රේරණතාවන්
වෙනස් වන බව.
ටීවී
බූස්ටර්වල එහෙම පවතින කුඩා
කොයිල්වල පොටවල් මෙලෙස එහෙට
මෙහෙට කරන විට,
ටීවී
එකේ දර්ශනයේ පැහැදිලිකම වෙනස්
වන බව ඔබටම දැකිය හැකියි.
මෙම
සූත්රයට අමතරව වෙනත් සූත්ර
පොතපතේ සඳහන් වී තිබිය හැකියි.
ඊට
හේතු ඇත.
සමහර
සූත්ර සකස් කර තිබෙන්නේ
දිගවල් අඟල්වලින් දැක්විය
යුතු විදියටයි.
තවත්
ඒවා සෙන්ටිමීටර් හෝ මිලිමීටර්
හෝ අඩිවලින්ද දැක්විය යුතුය.
මෙලෙස
භාවිතා කරන ඒකක වෙනස් කරන විට,
සූත්රය
ටික ටික වෙනස් වේ (ඇත්තටම
ඔබටම ඉහත සූත්රයෙන් එම වෙනස්
සූත්ර සාදාගත හැකියි).
සූත්රය
වෙනස් වුවත්,
නිවැරදි
ඒකකවලින් ගණනය කරනවා නම්,
අවසන්
ප්රතිඵලය එකමයි.
තවද,
ඉහත
සූත්රයට වඩා වෙනස්ම ආකාරයේ
සූත්රද තිබිය හැකියි.
එහිදී
යොදන පරාමිතින්වල (parameter)
වෙනස්කම්
තමයි පවතින්නේ.
උදාහරණයක්
ලෙස,
ඉහත
සූත්රයේ තිබූ පරාමිතින්
තමයි u
(පාරගම්යතාව),
N (වට
ගණන),
A (කොයිලයේ
ක්ෂේත්රඵලය),
හා l
(කොයිලයේ
දිග)
වේ.
එහෙත්
පහත සූත්රය ඊට වෙනස්ය.
මෙහි පරාමිතින් ඊට පෙර සූත්රය වඩා වෙනස් නේද? මෙම සූත්රයටද දිගවල් මීටර්වලින් ලබා දෙන්න. හොඳින් මතක තබා ගන්න මෙම සූත්ර දෙකේ පරාමිතින් වෙනස් වූවාට (ඒ කියන්නේ සූත්රද විශාල ලෙස වෙනස් වූවාට), අවසානයේ ලැබෙන්නේ ආසන්න වශයෙන් එකම පිළිතුරයි. පොටවල් අතර හිඩැස් නොතබා ඔතන්න. තවද, ඉහත සූත්රය අනුව පෙනෙනෙවා වයරයේ ගේජ් එක අනුව ප්රේරණතාව වෙනස් වන බව. කම්බියේ ගේජ් එක අඩුවන විට ප්රේරණතාව වැඩි වේ. ඒ කියන්නේ යම් පරිපථයක ඔබට අහවල් ගේජ් එකේ කම්බියක් වටවල් අච්චර ප්රමාණයක් ඔතන්න යැයි කියා ඇති විටක, එම ගේජ් එකට වැඩි ගේජ් එකක් නම් ඔබ සතුව ඇත්තේ, වැඩිපුර වට ප්රමාණයක් එතිය යුතු බව පෙනෙනවා නේද? මෙලෙස මහත වැඩි කම්බියකින් ආදේශ කළත්, කියා තිබෙන කම්බි ගණකමට වඩා අඩු ගණකමක් සහිත කම්බියක් නම් යොදා ගන්න එපා. ඉහත සූත්රය යොදාගෙන එම අමතරව එතිය යුතු වටවල් ගණනද සොයා ගත හැකියි.
තවද,
ඉහත
සූත්ර දෙකෙහිම පැහැදිලිවම
පෙනෙනවා කොයිල් එකේ රවුමේ
විශාලත්වය වෙනස් වන විට,
ඉන්ඩක්ටන්ස්
එක වෙනස් වන බව.
කොයිලයේ
රවුම විශාල වන විට,
ප්රේරණතාව
වැඩි වේ.
එනිසා,
උදාහරණයක්
ලෙස,
පැන්සලක්
වටා අච්චර ප්රමාණයක් වටවල්
ඔතන්න කී විට,
ඔබ එය
කොසු මිටක් වටා එතුවොත්
ප්රශ්නයක් වේවි.
සෑම
සූත්රයකම u
හෝ
uru0
ලෙස
පාරගම්යතාවක් ඇත.
මෙයත්
ඉතා වැදගත් සාධකයක්.
කොයිලය
මැද තිබෙන ද්රව්ය වෙනස් වන
විට,
මෙම
අගය වෙනස් වේ.
කිසිවක්
කොයිලය තුල දමා නැති විට,
එහි
තිබෙන්නේ වාතයයි.
එවිට
වාතයේ (රික්තයේ)
පාරගම්යතා
අගය ඊට ආදේශ කළ යුතුයි.
වැඩි
පාරගම්යතාවන් සහිත ද්රව්යක්
තිබීමෙන් විශාල ලෙස ප්රේරණතාව
වැඩි කල හැකියි.
බහුලව
යොදා ගන්නා එවැනි ද්රව්ය
කිහිපයක් ඇත.
ෆෙරයිට්
(ferrite)
හා
මෘදු යකඩ (soft
iron) ඒ
අතර ප්රමුඛ වේ.
මෙම
ද්රව්ය සුමට "බට"
ආකාරයට
පවතිනවා.
ඒවා
කෝර් (core)
ලෙසද
හැඳින් වෙනවා.
එවිට,
ඔබට
අවශ්ය විශ්කම්භය සහිත කෝර්
එකක් ගෙන කම්බි ඒ වටා ඉතා තදින්
එතිය යුතුය.
කෝර්
එක අනුව ඉන්ඩක්ටරයේ සංඛේතයද
වෙනස් කරන සම්ප්රදායක් ඇත
(ඉන්ඩක්ටර්
පාඩමේ මුලම මෙම සංඛේත සියල්ල
දැක්වූවා).
නැවතත්
එම සංඛේත පහත දැක්වෙනවා.
දළ වශයෙන් ඇලුමිනියම්, තඹ, රිදී, ඊයම්, ලී, කොන්ක්රිට්, ජලය, වාතය, රික්තකය යන සියල්ලෙහිම පාරගම්යතාව සමානය; එනම් සාපේක්ෂ පාරගම්යතාව (ur) එකට සමාන වේ. 99.8%ක් පිරිසිදු යකඩ වල සාපේක්ෂ පාරගම්යතා අගය 5000 පමණද, 99.95% පිරිසිදු යකඩවල එය 200,000 පමණද, මෘදු වානේවල 2000ක පමණ අගයක්ද, ෆෙරයිට්වල එම අගය සිය ගණනක් දක්වා විය හැකියි. යකඩ අඩංගු මිශ්ර ලෝහවලත් සාපේක්ෂ පාරගම්යතාව එකට වඩා විශාල ලෙස වැඩිය. ඔබට ඉහත පෙනුන විදියටම, මෙම අගය එම ද්රව්යයේ පිරිසිදුබව හා ඊට මිශ්ර වී ඇති වෙනත් සංඝඨක අනුව වෙනස් වෙනවා. එම කෝර් එකේ පවතින උෂ්ණත්වය මතද සුලු වශයෙන් තමන්ගේ පාරගම්යතා අගය වෙනස් කර ගන්නවා.
ඒ
විතරක්ද නොවේ,
මෙම
කෝර් එක ඉන්ඩක්ටරය හරහා ගලා
යන සංඥාවේ සංඛ්යාතයටද සංවේදී
වෙනවා.
ඒ
කියන්නේ සමහර ද්රව්ය
අධිසංඛ්යාත සමග යොදන්නට
බැහැ.
ඒ එක්
එක් ද්රව්ය සපෝට් කරන උපරිම
සංඛ්යාතයක් පවතිනවා.
රික්තයකයට
නම් මෙවැනි උපරිම සංඛ්යාතයක්
නැත (ඊට
ඕනෑම සංඛ්යාතයක් දැරිය
හැකියි);
මෙය
කෝර් නොමැති ඉන්ඩක්ටර්වල
තිබෙන ප්රබල වාසියකි.
මෙය
තරමක් පැහැදිලි කර ගමු.
ඒසී
සංඥාවක් ඉන්ඩක්ටරය හරහා ගලා
යන විට,
කෝර්
එක සෑදී තිබෙන අංශුද ධ්රැවීකරණයකට
ලක් වෙනවා (ඒ
කියන්නේ එක පැත්තකට ධාරාව
ගලන විට,
අංශු
යම් දිශාවක් ඔස්සේ ස්ථාන ගත
වෙනවා;
ඊළඟ
මොහොතේදී අනෙක් දිශාවට ධාරාව
ගලන විට,
අංශු
තමන් සිටි දිශාවට විරුද්ධ
පැත්තේ ස්ථාන ගත වෙනවා).
අඩු
සංඛ්යාතවලදී මෙය එතරම්
ගැටලුවක් නැතිව කළ හැකි වුවත්,
සංඛ්යාතය
වැඩි වන විට,
අංශු
එහාට මෙහාට ස්ථානගත වීමට හරි
හැටි ගමන් කරන්නට බැරි වෙනවා.
එවිට
පාරගම්යතාව වෙනස් වෙනවා.
ඉහළ
හෝ පහළ හෝ ඕනෑම සංඛ්යාතයකදී
අංශු ධ්රැවීකරණය වෙන බව
පැහැදිලියිනෙ.
අංශු
එහාට මෙහාට නිකං සෙලවෙන්නේ
නැත.
ඊට
බලයක්/ශක්තියක්
වැය වෙනවා.
මෙම
ශක්තිය කෝර් එක විසින් ලබා
ගන්නේ චුම්භක ක්ෂේත්රයෙනි;
එනම්
ඉන්ඩක්ටරයෙනි.
මේ
අනුව,
කෝර්
එකක් යොදන විට,
ඉන්ඩක්ටරයෙන්
යම් කුඩා ශක්තියක් අපතේ යන
බව පැහැදිලියි නේද?
සංඛ්යාතය
වැඩි වන විට,
එම
අපතේ යන ශක්තියද වැඩි වෙනවා.
මෙම
අපතේ යන ශක්තිය අවසානයේ තාපය
බවට පත් වෙනවා.
එනිසා
කෝර් රත් වෙනවා.
තවද,
චුම්භක
ක්ෂේත්රයේ ත්රීව්රතාවද
කෝර් එකේ පාරගම්යතාවට බලපෑමක්
ඇති කරනවා.
මුලදී
පෙන්වා දුන්නා B=uH
යන
සම්බන්ධතාව.
යම්
චුම්භකයක මෙම B
හා H
යන
දෙකම එකවර පවතිනවා.
මෙම
සරල සූත්රය බැලූබැල්මට
කියන්නේ ඔබ යම් (H
හෝ B)
අගයක්
දන්නේ නම්,
ඉතා
පහසුවෙන්ම අනෙක් අගය සොයා ගත
හැකියි කියාය.
එහෙත්
තත්වය එසේ නොවේ.
ඊට
හේතුව u
නියතයක්
නොවේ.
උෂ්ණත්වය
ආදී හේතු මත එය වෙනස් වූවා
සේම,
ස්රාව
ඝනත්වය (B)
මතද
එය වෙනස් වෙනවා.
එය
සිදු වන්නේ මෙසේය.
යම්
චුම්භකයක් (විද්යුත්
චුම්භකයක්)
ගන්න.
එහි
චුම්භකතාව (H)
වැඩි
කරගෙන යන්න.
එවිට,
B ද ඊට
සමානුපාතිකව වැඩි වෙනවා යම්
මොහොතක් දක්වා.
එම
මොහොත සංතෘප්ත අවස්ථාව
(saturation
point) ලෙස
හැඳින්වෙනවා.
මෙම
සැචුරේෂන් පොයින්ට් එකට පසුව
ස්රාව ඝනත්වය වැඩිවීම සුපුරුදු
පරිදි සිදු නොවේ.
එනම්,
H වැඩි
වුවත් B
වැඩි
නොවන තරම්ය.
පහත
රූපයේ මෙය පැහැදිලිව දැක්වේ.
මෙය
සිදු වීමට හේතුව සරල භෞතික
විද්යාත්මක කාරණයකි.
චුම්භකතාව
(H)
යනු
සුපර්වයිසර් කෙනෙකි.
එනම්,
අනෙක්
අය ලවා වැඩ කරවයි.
එහෙත්
සුපර්වයිසර්ට වුවත් මිනිසුන්ගෙන්
වැඩගත හැකි උපරිම ප්රමාණයක්
තිබේ.
මෙවැන්නක්ම
තමයි චුම්භකය තුළත් සිදු
වන්නේ.
H විසින්
සිදු කරන්නේ චුම්භකය තුළ තිබෙන
"කුඩා
චුම්භක අංශු"
ලවා
වැඩ ගැනීමයි (එනම්,
එක එක
දිශාවලට පිහිටා තිබෙන එම අංශු
H
හි
දිශාව ඔස්සේ පවත්වාගෙන යෑමයි
(align)).
මෙම
අංශුවල ක්රියාකාරිත්වය තමයි
ස්රාව ඝනත්වය ලෙසට අපට
දිස්වන්නේ.
ක්රමයෙන්
H
වැඩි
කරගෙන යන විට තව තවත් එම අංශු
"වැඩ
කරයි";
එනම්
B
වැඩි
වේ.
එහෙත්
එක්තරා අවස්ථාවකදී එම අංශු
සියල්ලටම කළ හැකි උපරිම මට්ටම
ළඟා වෙනවා.
එවිට
කොච්චර H
(සුපර්වයිසර්)
වැඩ
කරන්න යැයි බල කළත් අංශුවලට
ඊට වඩා වැඩක් කිරීමට බැරි
වෙනවා.
මෙම
විස්තරය අනුව,
B = uH නිසා,
B හා H
දිගටම
ඒකාකාරව වෙනස් වෙනවා වෙනුවට
එක එක සීඝ්රතාවලින් වෙනස්
වෙනවා යන්නෙහි තේරුම u
වෙනස්
වෙනවා යන්නයි.
ඉහත
අපූරු ක්රියාකාරිත්වය
හඳුන්වන්නේ magnetic
hysteresis කියාය.
මෙය
ඇත්තටම කරදරයකි ඉන්ඩකටර්
සෑදීමේදී.
යම්
කෝර් එකක් වටා ඔතා තිබෙන
කොයිලයක් ගමු.
ඊට
විදුලිය සපයා ක්රමයෙන් ධාරාව
වැඩි කර ගෙන යන්න.
එවිට
ක්රමයෙන් H
වැඩි
වේගෙන යනවා.
මෙම
H
වැඩි
වේගෙන යන විට,
B ද
ක්රමයෙන් වැඩි වේගෙන යනවා
(පහත
රූපයේ O
සිට
a
දක්වා
කොටසින් පෙන්වන්නේ මෙයයි).
එහෙත්
සැචුරේෂන් පොයින්ට් එකේදී
එම වැඩිවීමත් නවතිනවා (ඉහත
විස්තර කළ පරිදි).
දැන්
ධාරාව නැවත ක්රමයෙන් අඩු
කරගෙන යන්න.
එවිට,
H ද
ක්රමයෙන් අඩු වේගෙන යනවා.
එවිට,
B ද
ක්රමයෙන් අඩු වේගෙන යනවා.
එහෙත්
මෙහිදී B
අඩු
වෙන්නේ මුලින් (o
සිට
a
දක්වා
කොටස)
වැඩි
වූ සීඝ්රතාවෙන් නොව,
ඊට වඩා
අඩු සීඝ්රතාවකිනි.
රූපයේ
a
සිට
b
දක්වා
නිරූපණය කරන්නේ මෙයයි.
බලන්න
b
අවස්ථාවේදී
H
ශූන්ය
වුවත්,
යම්
B
අගයක්
කෝර් එක තුළ පවතිනවා නේද?
(එහෙත්
ආරම්භයේදී H
ශූන්ය
වූ විට B
ද ශූන්ය
විය.)
මින්
කියන්නේ කුමක්ද?
කෝර්
එකේ යම් ස්රාව ඝනත්වයක් (B)
පවතිනවා
යැයි කියන්නේ එහි කාන්දම්
ගතියක් පවතින බවයි.
එනම්
කෝර් එක දැන් කාන්දම් කෑල්ලක්
බවට පත් වෙලා.
යම්
යකඩ කැබැල්ලක් වටා කොයිල්
කැබැල්ලක් ඔතා විදුලි ධාරාවක්
කොයිලය හරහා යම් සුලු කාලයක්
තිස්සේ යැවූ විට,
එම යකඩ
කැබැල්ල කාන්දම් කෑල්ලක් බවට
පත්වෙන වෙනව බව බොහෝ විට ඔබ
අත් දැක ඇති.
ඉහතදී
කෝර් එකට සිදු වූවෙත් එයයි
(කොයිලයේ
ධාරාව මොහොතක් යවා,
ධාරාව
නතර කළ පසු කෝර් එක කාන්දම්
කෑල්ලක් බවට පත් වී ඇත).
හරි,
තවදුරටත්
ඉහත ක්රියාකාරකම ඉදිරියට
කරගෙන යමු.
දැන්
ධාරාව (ඒ
කියන්නේ H)
විරුද්ධ
දිශාවට ක්රමයෙන් වැඩි කරගෙන
යන්න (b
සිට
c
දක්වා).
දැන්
කෝර් එකේ තිබූ කාන්දම් ගතිය
ක්රමයෙන් අඩු වී ගෙන ගොස්
ශූන්ය බවට පත් වේ (c
අවස්ථාවේදී).
තවදුරටත්
මෙම දිශාවට ධාරාව වැඩි කරගෙන
යන විට,
B ද තමන්
මුලින් සිටි දිශාවට විරුද්ධ
දිශාව ඔස්සේ අලුත් ක්ෂේත්රයක්
පවත්වා ගන්නවා (c
සිට
d
දක්වා).
මෙලෙස,
ධාරාව
වැඩි කරගෙන ගොස් යම් තැනකදී
එම දිශාව ඔස්සේ සැචුරේෂන්
පොයන්ට් එක හමු වෙනවා.
ඒ
කියන්නේ මෙම අවස්ථාවේදී කොච්චර
H
වැඩි
කළත් B
වැඩි
වෙන්නේ නැත.
දැන්
නැවත ධාරාව ක්රමයෙන් ශූන්ය
කරා ගෙන එන්න (d
සිට
e).
මෙහිදීද
පෙර සේම,
ධාරාව
නැවැත්වූ පසුත් කාන්දම් ගතිය
කෝර් එකේ පවතිනවා.
එහෙත්
මෙහිදී කාන්දම (කෝර්
එක)
පෙර
තිබූ උතුර හා දකුණ යන දෙක මාරු
වෙලායි පිහිටන්නේ.
දැන්
ක්රමයෙන් නැවත ධාරාව විරුද්ධ
පැත්තට වැඩි කරගෙන යන විට (e
සිට
a)
B ද
විචලනය වන අයුරු රූපයේ බලන්න.
මෙම
රූපයේ පෙනෙන ආකාරයට කෝර් එක
යම් B
අගයකට
පසුව සංතෘප්ත වන බව වටහා ගන්න.
මෙම
සංතෘප්ත වීම විදුලියේ ධන හා
ඍණ පැති දෙකෙහිම සිදු වෙනවා.
විදුලි
ධාරාව නිසා කෝර් එකේ යම් කාන්දම්
බලයක් ඉතිරි වීම ප්රශ්නයකි.
ඊට
හේතුව,
ඒසී
ධාරාව නිරන්තරයෙන් පැති මාරු
කරනවා.
එවිට,
මේ සෑම
පැති මාරු කිරීමකදීම ශක්තිය
හානි වේ.
මෙහෙම
සිතන්න.
එක
පැත්තකට ධාරාව දැන් ගමන්
කරනවා.
එවිට
ධාරාව නතර වුවත් කෝර් එකේ යම්
කාන්දම් ශක්තියක් ඉතිරි වේ.
ආපස්සට
ධාරාව ගලන විට,
එම
අලුත් දිශාවට අලුතින් චුම්භක
ස්රාව ඝනත්වය පිහිටු වීමට
පෙර මුලින් විරුද්ධ පැත්තට
යොමුවී තිබෙන ඉතිරි වූ කාන්දම්
ශක්තිය ඉවත් කිරීමට සිදු
වෙනවා.
එය
ඉවත් කළ පසුයි,
අලුත්
දිශාවට ක්ෂේත්රය පිහිටුවිය
හැක්කේ.
ඉතිං
මෙලෙස ශක්තියක් වැය කොට තිබූ
කාන්දම් බලය ඉවත් කර අලුත්
දිශාවට ස්රාව ඝනත්වය පිහිටනවා.
එලෙසම,
ධාරාවේ
දිශාව නැවත මාරු වන විට,
මෙම
දිශාව ඔස්සේ ස්රාව ඝනත්වය
පිහිටුවීමට පෙර,
ඊට පෙර
අවස්ථාවෙන් ඇති වූ (විරුද්ධ
දිශාවට පිහිටි)
කාන්දම්
බලය අහෝසි කළ යුතු වෙනවා.
මේ
ආකාරායට දිගින් දිගටම ශක්තිය
හානි වෙනවා මෙම ඉතිරි වූ කාන්කම්
බලය ඉවත් කිරීමට.
මෙම
ශක්ති හානියම තමයි මීට පෙර
සංඛ්යාතය ගැන කතා කරන විට
හමු වූයෙත්.
සංඛ්යාතය
වැඩිවන විට මෙම ක්රියාව
වේගයෙන් සිදු වන නිසා වේගයෙන්
(වැඩිපුර)
ශක්ති
හානිය සිදු වෙනවා.
ඇත්තටම
මට මෙහිදී පෙන්වා දීමට අවශ්ය
වූයේ ශක්තිය හානිය සිදු වන
වග පෙන්වීමටම නොවේ;
සංතෘප්ත
වීම පෙන්වීමයි.
කෝර්
එක සංතෘප්ත නොවන අයුරින් තමයි
ඉන්ඩක්ටරය සෑදිය යුත්තේ.
ඒ
කියන්නේ ඔබගේ ඉන්ඩක්ටරයේ ඇති
වන උපරිම B
අගයට
ඔරොත්තු දෙන (එනම්,
එම B
අගයේදිත්
සංතෘප්ත නොවන)
ද්රව්යයක්
තමයි කෝර් එකට යෙදිය යුතු
වන්නේ.
දැන්
බලමු වෙනත් ආකාරයේ ඉන්ඩක්ටර්වලට
යෙදිය හැකි සූත්ර ගැන.
ඉලෙක්ට්රෝනික්ස් (electronics) ...












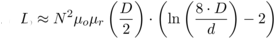








repair gena tiyana sait tikak denawada
ReplyDeletesinhalen repairing gena liyapu poth man dekala thiyenawa... library ekakin ho bookshop ekakin man hithanne oyata ewa ganna puluwan. english walin nam ona tharam internet eke owa gena thibunath, sinhalen thiyeda kiyala man danne na. poddak google eke search karala balanna.
ReplyDeletepcb board ekak hadaganna vidiha kiyala den nedda perek coraid krame dannawa wena ekak nedda
ReplyDeleteapi idiriyedi e genath katha karamu. :) liyanna nam boho dewal thiyenawa... eheth ithin welawa thamai hoya ganna ona... ethek man liyapu ewa kiyawala balanna...
ReplyDelete