රේඛීය පරිනාමනය
ශ්රිතයක්
පහත කොන්දේසි දෙකම සපුරන විට,
එම ශ්රිතයේ
රේඛීය ලක්ෂණ තිබෙන බව හෙවත්
එම ශ්රිතය රේඛීය ශ්රිතයක්
යැයි කියනවා.
1. f(ax) = af(x)
2. f(x + y) = f(x) +f(y)
උදාහරණයක්
ලෙස,
d(4x3+x2)/dx යන
අවකලනය රේඛීය පරිනාමන ලක්ෂණය
සහිත වේ මොකද එය 4dx3/dx
+ dx2/dx ලෙස
ලියා සුලු කළ හැකිය.
ඛණ්ඩාංක
පද්ධතියක තිබෙන යම් ලක්ෂ්යයක්
ගත් විට එය අපට විවිධාකාරයෙන්
වෙනස් කළ හැකිය.
මෙවැනි
වෙනස් කිරීම් ඉහත කොන්දේසි
දෙක සපුරන ලෙස සිදු කරන විට
රේඛීය පරිනාමනය (linear
transformation) ලෙස
හැඳින්වෙනවා.
යම්
ලක්ෂ්යයක් පිහිටුම් දෛශිකයක්
ලෙස නිරූපණය කළ හැකි නිසා,
දෛශිකද
ඉහත කොන්දේසිවලට යටත්ව
පරිනාමනයන් සිදු කරන විට දෛශික
පරිනාමනය (vector
transformation) ලෙසද
එය හැඳින්වේ.
රේඛීය පරිනාමනය
ජ්යාමිතික වුවත්,
ක්රියාත්මක
වන්නේ ශ්රිත මෙන්ය;
එනම් යම්
ලක්ෂ්යයකට අදාල අගයන් ඇතුලු
කළ විට,
එම දෛශිකය
මත යම් පරිනාමයනයක් සිදු වී
එම පරිනාමනය වූ ලක්ෂ්යයේ
අගයන් පිට කරයි.
විද්යාව
හා තාක්ෂණයේදි රේඛීය/දෛශික
පරිනාමනය ඉතා වැදගත් තැනක්
උසුලයි.
පළමුව ඒ
ගැන ඉතා කෙටියෙන් බලමු.
පරිනාමනය
රේඛීය බව පහත ආකාරයට සාධනය
කළ හැකිය.
පදනම්
දෛශික 4ක
පද්ධතියක ඒ ඒ පදනම් දෛශික පහත
ආකාරයට තීරු න්යාස ලෙස නිරූපණය
කළ හැකියි.
ඉහත එක් එක්
පදනම් දෛශිකය මත සිදු කරන
රේඛීය පරිනාමනයන් පහත ආකාරයට
ඉදිරිපත් කළ හැකිය (පහසුව
තකා පදනම් දෛශික දෙකක පද්ධතියක්
පමණක් සලකමු).
මෙය තේරුම්
ගත යුත්තේ මෙසේය.
(1,0) යනු
පලමු පදනම් දෛශිකයනෙ.
ඒ මත සිදු
කරන පරිනාමය (L)
තමයි
(3,2) ලෙස
ඇති තීරු න්යාසයෙන් පෙන්වන්නේ.
දැන් අපි
බලමු ඉහත පරිනාමනය (-3,
4) යන
ලක්ෂ්යය මත සිදු කරන අයුරු.
පහත සුලු
කිරීම තුල (1)
හා (2)
යනු රේඛීය
කොන්දේසි දෙක බව පෙනේ.
අවසානයේ
ලැබී තිබෙන පිලිතුර වන (-17,14)
යනු
පරිනාමනයට ලක් වූ ලක්ෂ්යය
වේ.
ඛණ්ඩාංක
පද්ධතියක් මත යම් ලක්ෂ්යයක්
හෝ රේඛා ඛණ්ඩයක් දෛශිකයක්
ලෙස නිරූපණය කළ හැකියිනෙ.
මෙවැනි
ලක්ෂ්යයක් හෝ රේඛා ඛණ්ඩයක්
නිරූපණය කරන දෛශිකයක් අපට එම
ඛණ්ඩාංක තලය මත ප්රධාන ආකාර
කිහිපයකින් පරිනාමනය කළ
හැකියි.
පහත
දැක්වෙන්නේ එවැනි ප්රචලිත
පරිනාමන කිහිපයයි.
1. උත්තාරණය
(translation)
2. ප්රතිබිම්භනය
(reflection)
3. භ්රමණය
(rotation)
4. විස්තාරණය
(dilation)
යම් දෛශිකයක
පදනම් දෛශික හා සංරචක පේලි
හා තීරු න්යාස දෙකක ගුණිතයක්
ලෙස දැක්විය හැකි බව මොහොතකට
පෙර දැක්කා.
එලෙසම
යම් දෛශිකයක් මත සිදු කරන
පරිනාමනයන්ද න්යාසයකින්
නිරූපණය කළ හැකිය පහත ආකාරයට.
මෙවිට
න්යාසයකින් පරිනාමනය නිරූපණය
කෙරේ. මෙම
න්යාසය (aij)
එනිසා
පරිනාමන න්යාසය (transformation
matrix) ලෙස
හැඳින්වේ.
ඉහත පෙනෙන
ලෙස ඒකක/පදනම්
දෛශික ඔස්සේ පවතින සංරචක මත
පරිනාමන න්යාසය යොදා සුලු
කළ විට අපට ලැබෙන්නේ පරිනාමනය
වූ සංරචක සෙට් එකයි.
මීට පෙර
ගත් උදාහරණයම දැන් පරිනාමන
න්යාසයක් ආකාරයෙන් යොදා ගෙන
සුලු කර බලමු.
පරිනාමන
න්යාසය සෑදෙන්නේ එක් එක්
පදනම් දෛශිකයට අදාල අගයන්
සියල්ල පිලිවෙලින් තැබූ විට
ලැබෙන සංඛ්යා පදධතියෙනි.
බලන්න
පිලිතුර පෙර අවස්ථාවේදී ලැබුණු
පිලිතුරමයි.
එහෙත්
මෙහිදී ගණනය කිරීම කෙටි හා
පහසුය.
උත්තාරණයේදී
සිදු වන්නේ ඛණ්ඩාංක පද්ධතිය
මත තිබෙන යම් දෛශිකයක් එම
අවකාශයේ වෙනත් තැනකට ගෙන
යෑමයි.
එය හරියට
එක තැනක තිබෙන යම් භාණ්ඩයක්
උස්සන් ගිහින් තවත් තැනක තබනවා
වැනිය.
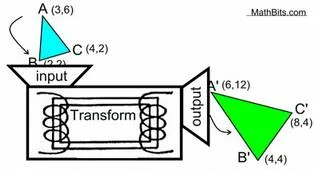
පහත රූපයේ
නිල්පාටින් පෙන්වා තිබෙන්නේ
රෝසපාටින් පෙන්වා ඇති ලක්ෂ්ය
සෙට් එකක උත්තාරණය කරපු ලක්ෂ්ය
සෙට් එකයි .
භ්රමණය
යනු යම් භ්රමන ලක්ෂ්යයකට
(center of
rotation) සාපේක්ෂව
යම් ලක්ෂ්යයක් දැන් තිබෙන
තැන සිට යම් කෝණයකින් කැරකීමයි.
ප්රතිබිම්භනයේදී
යම් ලක්ෂ්යයක් හෝ ලක්ෂ්ය
සෙට් එකක් (pre-image)
යම් කිසි
නිශ්චිත අක්ෂයකට සාපේක්ෂව
ප්රතිබිම්භයක් ලෙස නිරූපණය
වන සේ ලක්ෂ්ය හෝ ලක්ෂ්ය සෙට්
එක (image)
සැකසේ.
විස්තාරණයේදී
සිදු වන්නේ යම් යම් ලක්ෂ්යය
සෙට් එකක (pre-image)
විශාලත්වය
ලොකු කුඩා කර,
එම හැඩයෙන්ම
යුත් පරිනාමනය වූ ලක්ෂ්ය
සෙට් එකක් (image)
ලබා
ගැනීමයි.
පරිනාමනය
වූ රූපය (image)
මුල්
රූපයට (pre-image)
වඩා විශාල
වන විට එය විශාලනය (enlargement)
ලෙසත්,
කුඩා වන
විට එය ඌනනය (reduction)
ලෙසත්
හැඳින්වේ.
ඉමේජ්
එක හා ප්රීඉමේජ් එක අතර විශාලන
අනුපාතය පරිමාන සාධකය/අනුපාතය
(scale
factor/ratio) ලෙස
හැඳින්වෙනවා.
මේ ආදි ලෙස
පරිනාමනයන් ගැන තවත් කරුණු
ඇති අතර ඒ ගැන සොයා බලන්න.
බොහෝ
කරුණු මේ සම්බන්දයෙන් ඉගෙනීමට
ඇති අතර,
තාක්ෂණයේදී
(පරිගනක
චිත්ර හා චලන රූප හෙවත්
animation වලදී)
මේවා
බහුලවම ප්රයෝජනයට ගැනේ.
දැන් නැවත
අයිගන්දෛශික වෙත යොමු වෙමු.
මෙයත්
එක්තරා විදියකින් රේඛීය
පරිනාමනයක් බව පැහැදිලියිනෙ
(මොකද
දිශාව වෙනස් නොවුණත් විශාලත්වය/දිග
ලොකු කුඩා වීම සිදු වෙනවා).
යම්
සමචතුරස්ර න්යාසයක් A
ලෙස
සංඛේතවත් කරමු.
යම්
දෛශිකයක් X
ලෙස
සංඛේතවත් කරමු.
එවිට,
එම දෛශිකය
මත එම සමචතුරස්ර න්යාසය
යෙදූ විට,
එය AX
හෝ [A]{X}
ලෙස
සංඛේතවත් කළ හැකියි.
ඒ කියන්නේ
X දෛශිකය
මත A පරිනාමන
න්යාසයෙන් යම් පරිනාමනයක්
සිදු වේ.
අයිගන්දෛශිකයකදී
සිදුවන පරිනාමය වන්නේ X
දෛශිකයේ
විශාලත්වය පමනක් ලොකු කුඩා
වීමයි (scaling).
එනිසා X
නම් දෛශිකය
λ
නම්
අගයකින් (විශාලත්වය)
ලොකු
කුඩා වීම λX
හෝ
λ{X}
ලෙස
ලිවිය හැකියි (දෛශික
ගුණාකාරය).
ඉතිං,
A නම්
න්යාසයෙන් සිදු කරන්නේද එයම
නිසා පහත ආකාරයට සම්බන්දතාවක්
ගොඩනැඟිය හැකියි.
AX
= λX
දැන් අපට
කරන්නට තිබෙන්නේ ඉහත සම්බන්දතාව
තෘප්ත කෙරෙන පරිනාමන න්යාසය
(A)
කුමක්ද
යන්න සෙවීමයි.
එය
සොයන්නේ පහත ආකාරයට සුලු
කිරීමෙනි.
සමීකරණයේ
දෙපස සමාන කොටස් (පදනම්
දෛශික සෙට් එක)
කපා
දැමේ.
තවද,
සමීකරණයක්
නිසා,
වම්
පැත්තේ තිබෙන්නේ න්යාසයක්
බැවින්,
දකුණු
පසද වම් පස න්යාසයේ ගණයම
තිබෙන න්යාසයක් තිබිය යුතුය.
එහෙත්
දකුණු පස තිබෙන්නේ නිකංම නියත
පදයකි (λ).
එහි
වටිනාකම/අර්ථය
වෙනස් නොවී න්යාසයක් බවට
පත් කර ගන්නේ ඒකක න්යාසයෙන්
(I)
එම
නියත පදය වැඩි කිරීමෙනි.
ඉන්පසු,
දෙපසම
ඇති න්යාස නිශ්චායක බවට පත්
කර ගැනේ.
ඉන්පසු දකුණු
පස ඇති කොටස් වමට ගෙන ආ විට,
ඉහත අවසානයේ
දක්වා ඇති ආකාරයේ සමීකරණයක්
සෑදේ. එම
සමීකරණයේ A
න්යාසයේ
ලාක්ෂණික සමීකරණය
(characteristic/secular
equation of A) ලෙස
හැඳින්වේ.
ඉහත
උදාහරණයේ තෙවැනි ගණයේ න්යාසයක්
යොදා ගත්තද,
මෙම සියලු
විස්තර ඕනම ගණයක් සඳහා පොදුය.
දැන් එම
නිශ්චායක ආකාරයෙන් තිබෙන
සමීකරණය සුලු කරන විට පහත
ආකාරයට පත් වේවි.
(a11 -
λ)[(a22-λ)(a33-λ)
- (a23a32)] - a12[(a21)(a33-λ)
- a23a31] + a13[a21a32
- (a22-λ)a31]
= 0
කැමති නම්,
ඉහත සමීකරණය
තව දුරටත් සුලු කරන්න වෙන වෙනම
පද දක්වාම.
පෙනේවි
එය උපරිමව λහි
තෙවැනි බලයේ පදයකින් පටන්
ගන්නා සමීකරණයක් බව (k1λ3
+ k2λ2
+ k3λ + k4
ආකාරයේ).
දැන් මෙම
සමීකරණයේ මූල සෙවිය හැකිය.
මූල ගණන
සමීකරණයේ ඇති උපරිම බලයට සමාන
වේ. ඒ
අනුව මෙම උදාහරණයේදී මූල 3ක්
ලැබිය යුතුය.
මෙම මූල
A න්යාසයේ
ලාක්ෂණික මූල (characteristic
roots) හෙවත්
ගුප්ත මූල (latent
roots) හෙවත්
අයිගන්අගයන් (eigenvalues)
ලෙස හැඳින්
වෙනවා.
මෙම අයිගන්අගයන්
යනු එම න්යාසයට අදාල/ලාක්ෂණික
අගයන්ය (වෙනත්
න්යාසයකට එම අගයන් අදාල
නොවේ). එම
අයිගන්අගයන්ගෙන් කියන්නේ
දෛශික දිශාව වෙනස් නොකර
විශාලත්වය පමණක් වෙනස් කිරීමට
අවශ්ය නම් ගුණ කළ යුතු සංඛ්යා
වේ. මෙය
සියුම්ව තේරුම්ගත යුතු තත්වයකි.
ඒ කියන්නේ
යම් පරිනාමන න්යාසයක් යම්
දෛශිකයක් මත ක්රියාත්මක කළ
විට, එම
දෛශිකය පරිනාමනය වෙනවානෙ.
එය
පරිභ්රමණයක්,
ප්රතිබිම්භනයක්
හෝ වෙනත් පරිනාමනයක් විය
හැකියි.
එහෙත්
එම පරිනාමන න්යාසය ඊට ගැලපෙන
අයිගන් දෛශිකයක් මත ක්රියාත්මක
කළ විට සිදු වන්නේ දිශාව වෙනස්
නොවී විශාලත්වය පමණක් වෙනස්
කිරීමයි.
ඉහත විස්තර
මතකයේ රඳවා ගෙන උදාහරණයක්
ගෙන අයිගන්අගයන් සොයන හැටි
බලමු. පහත
ආකාරයට සුලු කර ගත් පසු අවසාන
වශයෙන් අයිගන්අගයන් දෙක 6
හා 1
ලැබුණි.
න්යාසය
දෙවැනි ගණයේ නිසා,
අයිගන්අගයන්ද
දෙකක් ලැබුණි.
අයිගන්අගයන්
මඟින් දැන් අපට හැකියි අයිගන්දෛශික
(eigenvector)
සොයන්නට.
කරන්නට
තියෙන්නේ λ
සඳහා ඉහත
ආකාරයට ලැබුණු අයිගන් අගයන්
ආදේශ කර [A
- λI]X
= 0 යන
සමීකරණය විසඳීමයි.
එය දැන්
කර බලමු.
සුලු කරන
විට පදනම් දෛශික දෙක (x,y)
සඳහා
සමීකරණ දෙකක් ලැබේ.
ඇත්තටම
x - 4y = 0 යන
සමීකරණය -1න්
ගුණ කළ විට -x
+ 4y = 0 ලෙස
ලැබෙන අතර,
එය ඊට පෙර
ලැබුණු සමීකරණයට සමානයි නේද?
(මෙලෙස
ලැබෙන සමීකරණ දෙකක් සමාන වීම
අහඹු සිදු වීමකි).
දැන් x
= 4y ලෙස හෝ
y = x/4 (හෙවත්
y/1 = x/4) ලෙස
සකස් කර ගෙන x,y
දෙකටම
කුඩාතම පූර්ණ සංඛ්යා එන පරිදි
අගයක් xට
හෝ yට
ආදේශ කරන්න.
x=4 ලෙස ගත
හැකිය;
එවිට y
= 1 වේ.
එනිසා 6
යන අයිගන්අගයට
අදාල අයිගන්දෛශිකය වන්නේ
(4,1) හෙවත්
4x + y (හෙවත්
4i + j) වේ.
එලෙසම අනෙක්
අයිගන්අගය ආදේශ කර නැවත ඉහත
සුලු කිරීම සිදු කරන්න.
නැවතත්
එකම සමීකරණය දෙපාරක් අහඹු
ලෙස ලැබී තිබේ.
එම සමීකරණයක්
y = -x ලෙස
පත් කරගෙන,
විචල්යය
දෙකටම පූර්ණ සංඛ්යා ලැබෙන
සේ ලබා දිය හැකි කුඩාතම/සරලතම
අගයක් එක් විචල්යයකට ආදේශ
කරන්න.
x=1 ලෙස ගත
හැකිය;
එවිට y
= -x = -1 වේ.
ඒ කියන්නේ
අයිගන්අගය 1
ට අදාලව
ලැබෙන අයිගන්දෛශිකය වන්නේ
(1,-1) හෙවත්
x - y (හෙවත්
i - j) වේ.
සාමාන්යයෙන්
එකිනෙකට වෙනස් අයිගන්අගයන්
ගණනට සමාන ගණනක් එකිනෙකට වෙනස්
අයිගන්දෛශික ලැබේ.
එකිනෙකට
වෙනස් අයිගන්දෛශික යනු රේඛියව
ස්වායත්ත දෛශික යනුයි.
එහෙත්,
මෙලෙස
ලැබෙන අයිගන්දෛශිකයක් ඕනෑම
නියත පදයකින් ගුණ කර අපට තවත්
ඕනෑ තරම් අයිගන්දෛශික සාදා
ගත හැකිය;
මෙලෙස
නියත පදයකින් ගුණ කර සාදා
ගන්නා නියත පද රේඛීයව ස්වායත්ත
නොවේ.
උදාහරණ
ලෙස, ඉහත
උදාහරණයේදී රේඛීයව ස්වායත්ත
අයිගන්දෛශික දෙක වූයේ (4,1)
හා (1,-1)
වේ.
(4,1) සැලකුවොත්
ඉන් රේඛීයව ස්වායත්ත නොවන
හෙවත් රේඛීයව පරායත්ත (linearly
dependent) අයිගන්දෛශික
අනන්ත ගණනක් සාදා ගත හැකියි
- 2(4,1) = (8,2),
3(4,1) = (12,3), 4(4,1) = (16,4), n(4,1) = (4n,n) ආදි
ලෙස.
තවත් උදාහරණයක්
ගමු. ඉහත
සිදු කළ ලෙසටම සුලු කිරීම සිදු
කළ විට පහත පෙන්වා ඇති පරිදි
අයිගන්අගයන් තුන ලෙස -2,
3, 6 යන අගයන්
ලැබේ.
දැන් ඉහත
අයිගන්අගයන් එකින් එක ආදේශ
කර මූලික (රේඛීයව
ස්වාධීන)
අයිගන්දෛශික
සොයමු.
දැන් අපට
අයිගන්දෛශික තුන ලබා ගැනීමට
අවශ්ය සමීකරණ 3ක්
ලැබී තිබෙනවා.
මේවා
සමගාමී සමීකරණ ආකාරයට හෝ ඔබ
දන්නා ඕනෑම ආකාරයකින් විසඳා
x,y,z අගයන්
ලබා ගත හැකියි.
එහෙත්
පලමු හා තෙවන සමීකරණ දෙක සමාන
බව පෙනේ.
සුලු කළ
විට අයිගන් දෛශිකය ලෙස (-1,0,1)
ලැබේ.
එලෙසම අනෙක්
අයිගන්අගයන් දෙකට අදාල
අයිගන්දෛශික දෙකත් ලබා ගත
හැකිය.
මෙතෙක් පුන
පුනා පැවසුවේ අයිගන්අගයකින්
සිදු වන්නේ දෛශිකයේ දිශාව
වෙනස් නොවී විශාලත්වය පමණක්
වෙනස් වෙනවා කියාය.
අයිගන්අගය
ඍන අගයක් (උදාහරණයක්
ලෙස -3 නම්)
නම් කුමක්
වේදැයි සිතා බලන්න.
අනිවාර්යෙන්ම
දෛශිකය 3
ගුනයක්
විශාල වේවි.
ඒ සමඟම
ඍන අගයක් නිසා,
දෛශිකයේ
දිශාව ප්රතිවිරුද්ධ වේ.
ඒ කියන්නේ
දිශාව වෙනස් වී ඇත.
ඇත්තටම
මෙය තමයි අයිගන්දෛශිකයක දිශාව
වෙනස් වෙනවා නම් වෙනස් විය
හැකි එකම ක්රමය (දිශාව
වෙනස් වීමක් ලෙස සාමාන්යයෙන්
එය සලකන්නේද නැත).
අයිගන්අගය
හැමවිටම තාත්වික සංඛ්යාවක්
වීම අත්යවශ්යද නැත.
එය සංකීර්ණ
සංඛ්යා (complex
number) වුවද
විය හැකිය.
අයිගන්අගයන්
සොයා ගත් පරිනාමන න්යාසයේ
අවයව සියල්ල තාත්වික සංඛ්යා
නම් හා එහි අයිගන්අගයන් ලෙස
සංකීර්ණ සංඛ්යා ලැබේ නම්,
හැමවිටම
මෙම සංකීර්ණ සංඛ්යාත්මක
අයිගන්අගයන් යුගල වශයෙන්
පැවතිය යුතුය (එනම්,
සංකීර්ණ
සංඛ්යාව හා එහි ප්රතිබද්ධය
යන යුගලය ලැබිය යුතුය).
සටහන
සංකීර්ණ
සංඛ්යාවක් ආකාර 3කින්
නිරූපණය කළ හැකිය.
පොදුවේ
එම ආකාර 3
වන්නේ a
+ bi, r(cosθ
+ isinθ),
reiθ
වේ.
යම්
සංකීර්ණ සංඛ්යාවක ප්රතිබද්ධය
(complex
conjugate) ලැබෙන්නේ
ඉහත ආකාර 3න්
එකකින් දක්වනු ලබන සංකීර්ණ
සංඛ්යාව a
- bi,
r(cosθ - isinθ),
re-iθ
වැනි
ආකාරයකින් ලියන විටයි.
අයිගන්දෛශික ගතිගුණ
අයිගන්දෛශික
සඳහා පහත සඳහන් ගතිගුණ අදාල
වේ. මා
මෙම ගතිගුණ මෙහිදී සාධනය කර
පෙන්වන්නේ නැත.
1. ඕනෑම
A නම්
සමචතුරස්ර න්යාසයක් හා එහි
A' නම්
පෙරලූ න්යාසය (transposed
matrix) යන
දෙකටම පවතින්නේ එක සමාන
අයිගන් අගයන් වේ.
2. ඕනෑම
ත්රිකෝණික න්යාසයක (triangular
matrix) හෝ
විකර්ණ න්යාසයක (diagonal
matrix) අයිගන්අගයන්
වන්නේ එහි ප්රධාන විකර්ණය
දිගේ පවතින අවයවවල අගයන් වේ.
3. යම්
තදේවභාවි න්යාසයක (idempotent
matrix) අයිගන්අගය
අනිවාර්යෙන්ම 0
හෝ 1
වේ.
4. යම්
න්යාසයක අයිගන්අගයන්වල
එකතුව එම න්යාසයේ ප්රධාන
විකර්ණය දිගේ පවතින අවයවවල
එකතුවට සමාන වේ.
5. යම්
න්යාසයක අයිගන් අගයන්ගේ මුලු
ගුනිතය එම න්යාසයේ නිශ්චායක
අගයට (එනම්,
එම න්යාසය
නිශ්චායකයක් සේ සලකා සුලු කළ
විට ලැබෙන අගයට)
සමාන වේ.
6. යම්
A නම්
න්යාසයක අයිගන් අගය ලෙස λ
පවතී
නම්,
එම
න්යාසයේ A-1
නම්
ප්රතිලෝම න්යාසයේ (inverse
matrix) අයිගන්
අගය 1/λ
ලෙස
පවතී.
7.
යම්
A
නම්
න්යාසයක අයිගන් අගයන් ලෙස
λ1,
λ2,
λ3,
..., λn
පවතී
නම්,
Am
(m යනු
ධන නිඛිලයකි)
නම්
න්යාසයේ අයිගන් අගයන් ලෙස
λ1m,
λ2m,
λ3m,
..., λnm
පවතී.
8.
යම්
ප්රලම්භක න්යාසයක (orthogonal
matrix) අයිගන් අගය
ලෙස λ
පවතී
නම්,
එහිම
තවත් අයිගන් අගයක් ලෙස 1/λ
පවතී.
9.
ඕනෑම
හර්මිෂන් න්යාසයක අයිගන් අගයන්
තාත්වික වන අතර,
කුටීක
හර්මිෂන් න්යාසයක අයිගන් අගයන්
ශූන්ය හෝ අතාත්වික වේ (තාත්වික
කොටසක් නැති සංකීර්ණ සංඛ්යා).
අයිගන් දෛශික
ගැන ගණිතමය පැත්තෙන් ඉහත
ආකාරයට ඉගෙන ගත්තත්,
එහි
භෞතික විද්යාත්මක පැතිකඩවල්
විවිධ හා බොහෝ වේ.
ඒ සියල්ල
ගැනම එකවර ඔබට සමහරවිට නොවැටහෙනු
ඇත.
ඒ ඒ
අවස්ථාවලදී අයිගන්දෛශික යොදා
ගත හැකි බව විවිධ විද්යාඥයන්/ගනිතඥයන්
විසින් විශාල අධ්යන කිරීමෙන්
පසුවයි තීරණය කර තිබෙන්නේ.
එනිසා,
එකවරම
ඔබට අහවල් වර්ගයේ ගැටලුවකට
අයිගන් දෛශික යොදා ගත හැකිය
යනුවෙන් අනුමාන කළ නොහැකිය.
කරන්නට
තිබෙන්නේ ඒ ඒ විෂය ක්ෂේත්රයන්
ඉගෙන ගන්නා විට,
අයිගන් දෛශික
යොදා ගෙන ඒවා සුලු කළ හැකි බව
උගන්වන විට,
මේ ඔබ
උගත් අයිගන් දෛශික පිලිබඳ
දැනුම එවැනි අවස්ථාවලදී භාවිතා
කිරීමයි.
ඒ හැරත්,
අවශ්ය
නම්,
ඔබටද
මේ ගැන ගැඹුරු අධ්යනයන් සිදු
කර අයිගන් දෛශික යොදාගත හැකි
අලුත් අවස්ථා/පැතිකඩවල්
ලොවට හඳුන්වාදීමටද හැකිය.
සටහන
අයිගන්
(eigen)
යනු
ජර්මානු වචනයක් වන අතර එහි
තේරුම "තමා"
යන්නයි.
මෙම
වචනය අගය,
දෛශික
යන පද දෙක හැරුණහම තවත් ගණිත
වචන/සංකල්ප
කිහිපයක් සමඟම යෙදෙනවා.
උදාහරණයක්
ලෙස,
eigenfunction
(අයිගන්ශ්රිත)
යනු
එවැනි අවස්ථාවකි.
අයිගන්ශ්රිතයක්
යනු,
යම්
විචල්යයක් (හෝ
තවත් ශ්රිතයක්)
මත
ගනිත
කර්මයක්
ක්රියාත්මක වීම එම විචල්ය
(හෝ
ශ්රිතය)
යම්
නියත පදයකින් ගුණ කිරීමකට
සමාන වන අවස්ථාවයි.
පොදුවේ
එය Of(x)
= λf(x)
ලෙස
ලියමු (O
යන්නෙන්
ගනිත කර්මයක්ද,
λ
මඟින්
අයිගන්අගයද නිරූපණය කෙරේ).
උදාහරණයක්
ලෙස, ඔබ
දන්නවා යම් ශ්රිතයක්/විචල්යයක්
මත අවකලනය සිදු කළ හැකියිනෙ
(d f(x) / dx).
සමහර
ශ්රිත අවකලනය කරන විට එම
ශ්රිතයම හෝ එම ශ්රිතය තවත්
නියත පදයකින් ගුණ වී ලැබේ.
මීට හොඳම
උදාහරණය ex
හෝ eλx
වැනි
ඝාතීය ශ්රිතයි.
ඒ අනුව
ඝාතීය ශ්රිතයට සාපේක්ෂව
අවකලනය අයිගන්ශ්රිතයකි.
.












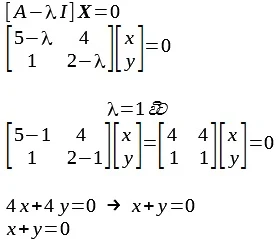



ඔබට මේක ලියනන්ම සෑහෙන වෙලාවක් යන්න ඇති. වෙනත් භාවකින් ඉගෙන ගත නිසා සිංහලෙන් අයිගන් අගයන් ගැන හෙම කියවන කොට අමුතුයි. අලුත් වචන කිහිපයක් ඉගෙන ගත්තා .
ReplyDeleteමේවා ඉගෙන තිබෙන අය අනිවාර්යෙන්ම ඉංග්රිසියෙන් තමයි ඕව ඉගෙන ඇත්තේ (මාත් ඇතුලුව) මොකද සිංහලෙන් මේ ගැන ලියා නැත (එවැනි පතපොත මට මෙතෙක් හමුවී නැත). ගූගල් කළ විට පාඩම් වශයෙන් පවතින්නේ මා ලියපු ඒවාය. මා මීට පෙරත් කමෙන්ටුවක ලියා ඇති ලෙසම, නැවත කියන්නට තිබෙන්නේ මේ දැනුම තිබෙන අය ඇයි මෙතෙක් කලක් සිංහලෙන් මේ ගැන ලියා නැත්තේ? ලංකාවේ අධ්යාපනයේ හා ඊනියා උගතුන්ගේ බංකොලොත්බව මින් මැනවින් පෙනෙනවා. මා දන්නා බොහෝ වෘත්තිකයන් (ඉංජිනේරුවන් ආදිය) සිටිනවා එතරම් ඉංග්රිසි දැනුමක් නැති (කොහොම උපාධි සමත් වූවාදැයි මා දන්නේ නැත). ඒ අය මෙවැනි ගණිත සංකල්ප කෙසේ ඉගෙන ගත්තාද, එම අවබෝධය කොහොමද කියා සැකසහිතයි. ඉංග්රිසියෙන් උසස් අධ්යාපනය ලබා දීම වැදගත්ය. එහෙත් අර වැනි ඉංග්රිසි දැනුම තවම ප්රමාණවත් නැති අයට ඉන් විශාල අසාධාරණයක් වේ. එනිසා විශ්ව විද්යාල පද්ධතිවල සිටින උගතුන්ට මේ එක් එක් විෂය සඳහා අඩුම වශයෙන් එක හොඳ පොතක් (comprehensive book) බැඟින්වත් ලිවීම අනිවාර්ය කළ යුතුයි ඔවුන්ට උසස්වීම් ලබා දෙන විට (ජ්යෙෂ්ට කථිකාචාර්ය, මහචාර්ය වැන).
Deleteමම ඉගෙන ගත්තේ රුසියානු භාෂාවෙන්. ඉන්පසු ඉංග්රීසියෙන්. එනිසා සිංහලෙන් අධ්යන පොදු සහතික උසස් පෙලින් පසු සිංහල භාවිතයක් තිබ්බේ නැහැ.
Delete//මා දන්නා බොහෝ වෘත්තිකයන් (ඉංජිනේරුවන් ආදිය) සිටිනවා එතරම් ඉංග්රිසි දැනුමක් නැති (කොහොම උපාධි සමත් වූවාදැයි මා දන්නේ නැත)// ලංකාවේ විවි වල උගන්වන්නේ සිංහලෙන්ද ඉංග්රීසියෙන්ද?
කොහොමත් ඔබේ කාර්යය හොඳයි. කීදෙනෙක් මේකෙන් ප්රයෝජනයක් ගන්නවද දන්නේ නැහැ හැබැයි.
ඔව්... එවැනි ජාතිකයන් තම බසින් ඒවා ඉගෙන ගන්නවා හා උගන්වනවා... ඒ සඳහා ඒ ඒ භාෂාවලින් ඕනෑ තරම් පොත්පත්ද තිබෙනවා. රුසියානු සමහර භෞතික විද්යා පොත්වල ඉංග්රිසි පරිවර්තන මා කියවාද තිබෙනවා. ඒවා බොහෝම අනර්ඝයි. ලංකාව එවැනිම තත්වයකට යාවිය හෝ යා හැකිද යන්න සැකසහිත වුවත්, ඉංග්රිසි දැනුම අඩු අය විශාල අසාධාරණයකට ලක් වෙනවා. ඉන්පසුව ඔවුන්ගෙන් සමාජයට අසාධාරණ සිදු වෙනවා. ඔව්, ලංකාවේ විජ්ජවිජ්ජාලවල උගන්වන්නේ ඉංග්රිසියෙන්.
Deletevectors wala pdf book ekath dannakoo.. kalin ewa wage
ReplyDeleteත්රිකෝණමිතිය පාඩම් මාලාවකුත් දෙන්න. ස්තූතියි . මේ වැඩේ හොදයි
ReplyDelete