අතිරේකය 1 (විද්යාව)
ඉලෙක්ට්රොනික්ස් යනු තාක්ෂණික විෂයක් නිසා විද්යාව හා ගණිතය ගැන අවබෝධය වැඩිවන තරමට තාක්ෂණික විෂයන් අවබෝධ කර ගැනීම පහසුය. මෙම අතිරේකයෙන් ඉලෙක්ට්රොනික්ස්වලට අවශ්ය යම් යම් සරල විද්යාත්මක කාරණා කිහිපයක් ගැන සාක්ච්ඡා කෙරේ.
මේ විශ්වයේ තිබෙන සියලුම දේවල් සරලව පදාර්ථ (matter) හා ශක්ති (energy) ලෙස දෙකොටසකට බෙදිය හැකියි. මේ සියල්ල පවතින්නේ “හිස් අවකාශය” (space) තුළයි. පදාර්ථයට යම් ස්කන්ධයක් (බරක්) සේම අවකාශයෙන් යම් ඉඩක්ද අවශ්ය වේ. ඇසට නොපෙනෙ තරමේ පවතින බැක්ටීරියාවක ස්කන්ධය හා එම බැක්ටීරියාව ගන්නා ඉඩ ප්රමාණය සිතා ගත නොහැකි තරම් ඉතා කුඩා වන අතර, ඈත තරුවක ස්කන්ධය හා අවකාශයේ ගන්නා ඉඩ ප්රමාණය සිතාගත නොහැකි තරම් විශාලය. මෙම සියලු පදාර්ථ ඝන (solid), ද්රව (liquid), වායු (gas) යන ආකාරවලින් පවතී. මෙම ආකාර පදාර්ථයේ අවස්ථා (states of matter) ලෙස හැඳින්වේ.
මේ නානාප්රකාරයේ සියලු පදාර්ථ සෑදී ඇත්තේ මූලික ද්රව්ය සියයක් පමණ ගණනක් මගිනි. මෙම මූලික ද්රව්ය මූලද්රව්ය (elements) ලෙස හැඳින්වේ. හයිඩ්රජන්, ඔක්සිජන්, කාබන්, යකඩ, ඇලුමිනියම්, තඹ, රත්තරං ආදී නම් වලින් ඒවා හැඳින් වේ. සෑම මූලද්රව්යක්ම තනි ඉංග්රිසි අකුරකින් (එය අනිවාර්යෙන්ම කැපිටල් විය යුතුය.) හෝ ඉංග්රිසි අකුරු දෙකකින් (ඉන් පළමු අකුර කැපිටල්ද දෙවන අකුර සිම්පල්ද විය යුතුය.) කෙටියෙන් හැඳින් වේ. මේ සියලු මූලද්රව්ය යම් කිසි රටාවකට සකසා ඇති වගුව ආවර්තිතා වගුව (periodic table) ලෙස හැඳින් වේ.
මේ සියලු මූලද්රව්යයන්වලට ඊටම අනන්ය (අනන්ය යන්නෙහි තේරුම ආවේණික යන්නයි.) වූ ගතිගුණ (properties) ඇත. මේ අතරින් ඕනෑම මූලද්රව්යයක් ගන්න. උදාහරණයක් ලෙස රත්තරං ගමු. ඔබ යම් රත්තරං කැබැල්ලක් ගෙන, එය දෙකට කඩන්න. දැන් කුඩා රත්තරං කැබැලි දෙකක් ලැබේ. කඩන්නට පෙරද තිබුණේ රත්තරංය; කැඩුවට පසුව තිබෙන්නේද රත්තරංය. දැන් කුඩා රත්තරං කැබැල්ල නැවත දෙකට කඩන්න. එවිටද නැවත ලැබෙන්නේ ඊටත් වඩා කුඩා රත්තරං කැබැලි දෙකකි. මේ ආකාරයට නැවත නැවත එය කඩා ගෙන යන විට, යම් අවස්ථාවක් එළඹෙනවා මෙය තවදුරටත් කැඩිය නොහැකි. මෙය පරමාණුව (atom) ලෙස හැඳින් වෙනවා. රත්තරං පරමාණුව යනු රත්තරංවල ගතිගුණ එලෙසම ඇති රත්තරංහි කුඩාම අංශුවයි (particle). දැන් ඔබට පැහැදිලියි රත්තරං කැබැල්ල සෑදී ඇත්තේ රත්තරං පරමාණුවලින් බව. මේ ආකාරයටම, ඇලුමිනියම් සෑදී ඇත්තේ ඇලුමිනියම් පරමාණුවලිනි. අනෙක් මූලද්රව්යයන්ද සෑදී ඇත්තේ ඒ ඒ මූලද්රව්යයේ නමින්ම හැඳින්වෙන පරමාණුවලිනි.
ඇත්තටම, පරමාණුවද නැවත කුඩා කොටස්වලට කැඩිය හැකිය. රත්තරං වේවා ඇලුමිනියම් වේවා හයිඩ්රජන් වේවා ඕනෑම පරමාණුවක් ඉලෙක්ට්රෝන (electron), ප්රෝටෝන (proton), හා නියුට්රෝන (neutron) යන කුඩා අංශු වර්ග තුනකට කැඩෙනවා. ඒ ඒ පරමාණු තුළ මෙම කුඩා අංශු විවිධ ප්රමාණවලින් පවතිනවා. උදාහරණයක් ලෙස, හයිඩ්රජන් පරමාණුවක් සෑදී තිබෙන්නේ එක් ප්රෝටෝනයක් හා එක් ඉලෙක්ට්රෝනයක් එකතු වීමෙනි. කාබන් පරමාණුවක් සෑදි තිබෙන්නේ ප්රෝටෝන හයකුත් ඉලෙක්ට්රෝන හයකුත් නියුට්රෝන හයකුත් එකතු වීමෙනි. මෙම අංශු තුනම පරමාණුවලට වඩා කුඩා නිසා, උපපරමාණුක (sub-atomic) අංශු ලෙස හැඳින්වෙනවා. එහෙත් මෙහිදී යම් ප්රශ්නයක් තිබේ. එනම්, ඉලෙක්ට්රෝනයක් තවත් ඉලෙක්ට්රෝනකයට වඩා කිසිම අයුරකින් වෙනස්කමක් නැත. ප්රෝටෝන හා නියුට්රෝන ගැනද කිව හැක්කේ එයමයි. උදාහරණයක් ලෙස රත්තරං පරමාණුවකින් ගත් ඉලෙක්ට්රෝනයක් හා ඔක්සිජන් පරමාණුවකින් ගත් ඉලෙක්ට්රෝනයක් අතර කිසිදු වෙනසක් නැත. කාබන් පරමාණුවකින් ගත් ප්රෝටෝනයක් හා වෙනත් ඕනෑම පරමාණුවකින් ගත් ප්රෝටෝනයක් අතර වෙනසක් නැත. එලෙසම, ඕනෑම පරමාණුවකින් ගත් නියුට්රෝනයක් තවත් ඕනෑම පරමාණුවකින් ගත් නියුට්රෝනයක් අතරද වෙනසක් නැත. එනිසා, යම් මූලද්රව්යයක ගතිගුණ එහිම පරමාණුව තුළ නොනැසී පැවතුනත්, යම් පරමාණුවක ගතිගුණ එම පරමාණුව සෑදී ඇති උපපරමාණුක අංශු තුළ පිහිටන්නේ නැත.
ඉලෙක්ට්රෝනයක ඍණ ආරෝපණයක් (-1) පවතී. එහි ස්කන්ධය ප්රෝටෝනයක ස්කන්ධයෙන් ආසන්න ලෙස දෙදහකින් පංගුවක් තරම් කුඩාය. එමනිසා, අප ඉලෙක්ට්රෝනයක ස්කන්ධය ශූන්ය ලෙස සලකනවා. ප්රෝටෝනයකට ධන එකක ආරෝපණයක් (+1) ඇත. නියුට්රෝනයක ස්කන්ධයද ප්රෝටෝනයක ස්කන්ධයට සමාන වන නමුත් නියුට්රෝනයකට කිසිදු ආරෝපණයක් නොමැත (උදාසීනයි). මේ අනුව යම් පරමාණුවක සම්පූර්ණ ස්කන්ධයට හේතුවන්නේ ප්රෝටෝන හා නියුට්රෝනවල ස්කන්ධවල එකතුව පමණක් බව පැහැදිලියි.
දැන් අප සලක් බලන්නේ ඉහත උපපරමාණුක අංශු විසින් ඒ ඒ පරමාණු සාදන්නේ කෙලෙසද කියා. යම් මූලද්රව්යයක පරමාණුවක් නිශ්චිතව හඳුනාගන්නේ එම පරමාණුව තුළ පවතින ප්රෝටෝන ගණන අනුවයි. යම් පරමාණුවක පවතින්නේ ප්රෝටෝන එකක් පමණක් නම්, එය හයිඩ්රජන් පරමාණුව ලෙස නම් කරනවා. යම් පරමාණුවක් ප්රෝටෝන දෙකක් ඇති නම්, හීලියම් ලෙස හැඳින් වෙනවා. මේ ආකාරයට ප්රෝටෝන තුනක් ඇති විට, ලිතියම් ලෙසද, හතරක් ඇති විට බෙරිලියම් ලෙසද, ආදී ලෙස ප්රෝටෝන එකින් එක වැඩි කරමින් විවිධ පරමාණු සෑදිය හැකි බව දැන් පැහැදිලියි නේද? යම් පරමාණුවක ඇති ප්රෝටෝන ගණන පරමාණුක අංකය (atomic number) ලෙස හැඳින් වෙනවා.
ඒ විතරක් නොවේ. යම් පරමාණුවක පවතින ප්රෝටෝන ගණනට සමාන ඉලෙක්ට්රෝන ගණනක් සැමවිටම පවතී. එහෙත් ප්රෝටෝන මෙන් නොව, යම් යම් අවස්ථාවලදී මෙම ඉලෙක්ට්රෝනවලින් එක් ඉලෙක්ට්රෝනයක් හෝ කිහිපයක් පරමාණුවෙන් පහසුවෙන්ම ගැලවී යෑමට හැකියි. තවත් අවස්ථාවකදී යම් පරමාණුවක් විසින් ඉලෙක්ට්රෝන පිටින් ලබා ගැනීමද සිදු කරයි. මේ අවස්ථා දෙකේදිම සිදුවන්නේ පරමාණුවේ පවතින ප්රෝටෝන ගණනට වඩා ඉලෙක්ට්රෝන ගණන වෙනස් වීමයි. ඇත්තටම මෙලෙස පරමාණුවක ඉලෙක්ට්රෝන වෙනස් වූ විට ඊට තවදුරටත් පරමාණුව කියන්නේ නැත. ඊට කියන්නේ අයනය (ion) කියාය. ඉලෙක්ට්රෝන ඉවත් වීමේදී (electron loss)ධන ආරෝපිත ප්රෝටෝන ගණනට වඩා ඍණ ආරෝපිත ඉලෙක්ට්රෝන ගණන අඩු නිසා, අයනයේ වැඩිපුර ඇත්තේ ධණ ආරෝපණයක් නිසා, එවැනි අයන ධණ අයන (positive ion) හෙවත් කැටායන (cation) ලෙස හැඳින්වෙනවා. එලෙසම, යම් පරමාණුවකට පිටතින් ඉලෙක්ට්රෝන ලබාගත් (electron gain) පසු, එම අයනයේ දැන් වැඩිපුර ඇත්තේ ඍණ ආරෝපණ බැවින්, එවැනි අයන ඍණ අයන (negative ion) හෙවත් ඇනායන(anion) ලෙස හැඳින්වෙනවා. සාමාන්යයෙන් පරමාණුවක ප්රෝටෝන හා ඉලෙක්ට්රෝන ගණන සමාන නිසා සමස්ථ පරමාණුව හැමවිටම උදාසීන (neutral) වේ.
තවද, යම් පරමාණුවක ඉහත ආකාරයට ප්රෝටෝන හා ඉලෙක්ට්රෝන ගණන නිශ්චය කළ හැකි වුවත්, එහි තිබෙන නියුට්රෝන ගණන නිශ්චිතවම කිව නොහැකිය. දළ වශයෙන් ප්රෝටෝන ගණනට සමාන නියුට්රෝන ගණනක් පවතී යනුවෙන් මතක තබා ගන්න. උදාහරණයක් ලෙස හයිඩ්රජන් පරමාණුව ගෙන බලමු. හයිඩ්රජන් යනු එක් ප්රෝටෝනයක් සහිත පරමාණුව නිසා එහි ඇත්තේ එක් ප්රෝටෝනයක් පමණි. ප්රෝටෝන ගණනට සමාන ඉලෙක්ට්රෝන ගණනක් ඇති නිසා, ඉලෙක්ට්රෝනද ඇත්තේ එකක් පමණි. එහෙත් හයිඩ්රජන් පරමාණුව තුළ නියුට්රෝන එකක්වත් නැත. ඇත්තටම බහුලව හමුවන හයිඩ්රජන් පරමාණුවල තත්වය එසේය. එනම්, හයිඩ්රජන් පරමාණුවලින් 99.98% ක ප්රතිශතයක් ඇත්තේ මෙම නියුට්රෝන එකක්වත් නැති හයිඩ්රජන් පරමාණුය (මෙම හයිඩ්රජන් සමස්ථානිකයට ප්රෝටියම් යන නමද භාවිතා කරනවා). මීට අමතරව, නියුට්රෝන එකක් පමණක් තිබෙන හයිඩ්රජන් පරමාණුද ඇත (මෙම හයිඩ්රජන් පරමාණුව ඩියුටීරියම් ලෙස හැඳින් වෙනවා). එය ප්රතිශතයක් ලෙස, 0.01% කි. එනම්, පරිසරයේ ඇති හයිඩ්රජන් පරමාණු දසදහසක් ගත් කළ, ඉන් 9998ක්ම නියුට්රෝන නොමැති වර්ගය වන අතර, ඉන් එකක් එක් නියුට්රෝනයක් සහිත වර්ගය වේ. එවිතරක්ද නොවේ, නියුට්රෝන දෙකක් තිබෙන හයිඩ්රජන් පරමාණු වර්ගයක්ද ඇත (මීට ට්රිටියම් කියා පවසනවා). එය පවතින්නේ ඊටත් වඩා අඩුවෙනි. මෙලෙස, යම් මූලද්රව්ය පරමාණුවක නියුට්රෝන ගණන විවිධ විය හැකියි. නියුට්රෝන ගණන වෙනස් වුවද, පරමාණුව එකම නමින් හැඳින් වේ. එහෙත්, එකම පරමාණුවේ මෙලෙස විවිධ නියුට්රෝන ගණනක් ඇති අවස්ථා සමස්ථානික (isotope)ලෙස හැඳින් වෙනවා. ඒ අනුව හයිඩ්රජන්වලට සමස්ථානික තුනක් තිබෙනවා. මේ ආකාරයට සෑම මූලද්රව්යයකටම සමස්ථානික කිහිපය බැගින් පවතිනවා. විවිධ මූලද්රව්ය ඇත්තේ එකසිය ගණනක් වුවද, එම සෑම මූලද්රව්යයකම පාහේ සමස්ථානික කිහිපය බැගින් ඇත. එවැනි සමස්ථානික සියල්ලම දහසකට වඩා පවතී. පරමාණුවක ඇති ප්රෝටෝන හා නියුට්රෝනවල එකතුවට පරමාණුක ස්කන්ධය (atomic mass) ලෙස කියනවා. යම් පරමාණුවක පරමාණුක සංඛේතය සමග පරමාණුක ක්රමාංකය හා පරමාණුක ස්කන්ධය කෙටියෙන් සටහන් කරන ක්රමයක් පවතිනවා. එය පහත රූපයෙන් දැක්වෙනවා.
(X-a ලෙසද මෙය කෙටියෙන් ලිවිය හැකියි. එවිට, පරමාණුක ක්රමාංකය සටහන් වන්නේ නැත. උදාහරණයක් ලෙස, ඉහත කාබන් පරමාණුව C-12 ලෙසද දැක්විය හැකියි.)
ඒ අනුව, හයිඩ්රජන්හි සමස්ථානික තුන පහත ආකාරයට ලිවිය හැකියි.
දැන් අප බලමු මෙම උපපරමාණුක අංශු පරමාණුව තුළ කුමන ආකාරයකින් පිහිටා තිබේද කියා. (අද වන විට, ක්වන්ටම් විද්යාවට අනුව ඉතා හොඳ ආකෘති තිබුණත්, ඉලෙක්ට්රොනික්ස්වලට එතරම් බරපතල ආකෘතියක් දැනට අවශ්ය නැත.) ප්රෝටෝන හා නියුට්රෝන පිහිටා තිබෙන්නේ පරමාණුවේ මැදයි. එය න්යෂ්ඨිය (nucleus) ලෙස හැඳින්වෙනවා. න්යෂ්ඨියේ පිහිටා ඇති නිසා ප්රෝටෝන හා නියුට්රෝන යන දෙකම පොදුවේ නියුක්ලියෝන(neucleon) යන නමින් හැඳින් වෙනවා.ඒ අනුව, යම් පරමාණුවක න්යෂ්ඨියේ ප්රෝටෝන දෙකකුත් නියුට්රෝන තුනකුත් ඇති විට, එම පරමාණුවේ නියුක්ලියෝන පහක් තිබේ යැයි කිව හැකිය. පරමාණුවේ ප්රමාණය සමග සැසඳීමේදී මෙම න්යෂ්ඨිය ඉතා කුඩාය. පරමාණුව විශාල ක්රීඩා පිටියක් තරම් යැයි උපමා කළොත් එහි න්යෂ්ඨිය එම ක්රීඩා පිටිය මැද තිබෙන කුඩා කඩල ඇටයක් තරම් ප්රමාණයේ වේ.
න්යෂ්ඨිය ඉතා ආරක්ෂිතව පවතී. එය කෘත්රිමව කැඩීමට ඉතා අපහසුය (උසස් විද්යා උපකරණ හා තාක්ෂණයක් ඊට අවශ්ය වේ.) ඇත්තටම මෙම න්යෂ්ඨියේ සියලු ප්රෝටෝන හා නියුට්රෝන පවතින නිසා, (ඉලෙක්ට්රෝනවල ස්කන්ධය ශූන්ය යැයි සලකන නිසාත්) පරමාණුවේ ස්කන්ධය පවතින්නේ මෙම න්යෂ්ඨිය තුලයි. න්යෂ්ඨිය එලෙස කුඩා වුවත්, පරමාණුව විශාල වීමට හේතුව ඉලෙක්ට්රෝන ඒ න්යෂ්ඨිය වටා ගමන් කිරීමයි. ඉලෙක්ට්රෝන සිතාගත නොහැකි තරම් වේගයෙන් මෙම න්යෂ්ඨිය වටා ගමන් කරනවා (හරියට මලක් වටා මීමැස්සන් කැරකෙනවා මෙන්). ඒ අනුව පෙනෙන්නේ පරමාණුවේ විශාලත්වයට එකම හේතුව ඉලෙක්ට්රෝන බවයි.
ඉලෙක්ට්රෝන න්යෂ්ඨිය වටා ගමන් කරන්නේද යම් ක්රමයකටයි. ඉලෙක්ට්රෝන සියල්ල ඔහේ එහේ මෙහේ යන්නේ නැත. ඒවා න්යෂ්ඨියේ සිට නිශ්චිත දුරවල්වලින් ගමන් කරනවා. උදාහරණයක් ලෙස, ඕනෑම පරමාණුවක පළමු ඉලෙක්ට්රෝන දෙක දක්වා ඉලෙක්ට්රෝන ගමන් කරන්නේ ඉලෙක්ට්රෝනයට ළඟින්ම ගමන් මාර්ගයකයි. ඉලෙක්ට්රෝන දෙකකට වඩා වැඩි පරමාණුවලදී, ඊ ළඟ ඉලෙක්ට්රෝන අට ගමන් කරන්නේ පළමු ඉලෙක්ට්රෝන දෙක ගමන් කළ දුරට වඩා වැඩි දුරකින් (ඈතින්) වේ. ඊ ළඟ ඉලෙක්ට්රෝන 18 ගමන් කරන්නේ ඊටත් වඩා දුරින් වූ මාර්ගයකයි. මෙලෙස තව තවත් ගමන් මාර්ග පිහිටයි. මෙම ක්රමයෙන් න්යෂ්ඨිය සිට ඈත් වන සේ පිහිටි ඉලෙක්ට්රෝන ගමන් මාර්ග ශක්ති මට්ටම් (energy level) ලෙස හැඳින්වෙනවා.
ඇත්තටම, පරමාණුවක අවසාන ශක්ති මට්ටමේ පවතින ඉලෙක්ට්රෝන නිසා ඒ ඒ පරමාණුවේ වැදගත් ගතිගුණ කිහිපයක් තීරණය වෙනවා. බොහෝ පරමාණුවලට යම් “දැඟලිල්ලක්” හෙවත් අස්ථාවර බවක් තිබෙනවා. විවිධ පරමාණුවල මෙම අස්ථායිතාව විවිධ ප්රමාණවලින් පවතී. ප්රධාන වශයෙන් අවසන් ශක්ති මට්ටමේ තිබෙන ඉලෙක්ට්රෝන විසින් මෙම අස්ථායිතාව තීරණය කෙරේ. අස්ථායි පරමාණු හැමවිටම බලන්නේ ස්ථායි වීමටයි. එය හරියට තරුණ ළමයින් වගේ. කොල්ලන් කෙල්ලන් පස්සේ යන්නේ ඔවුන්ගේ (ආදරයේ) අස්ථායි බව නැති කරගන්නටයි. කෙල්ලන්ද කොල්ලන්ට කැමැත්ත දෙන්නේ ඒ අයගේ අස්ථායිතාව ස්ථායි කර ගැනීමටයි. ගැහැණු පිරිමි ළමුන් ස්ථායි වන්නේ ආදරය හුවමාරු කර ගැනීමෙනි. පරමාණු ස්ථායි වන්නේ අවසන් ශක්ති මට්ටමේ ඇති ඉලෙක්ට්රෝන හුවමාරු කර ගැනීමෙනි. මෙලෙස විවිධ පරමාණු තමන්ගේම වර්ගයේ පරමාණුවක් සමඟ (උදාහරණයක් ලෙස හයිඩ්රජන් පරමාණුවක් තවත් හයිඩ්රජන් පරමාණුවක් සමඟ) හෝ යම් පරමාණුවක් වෙනත් වර්ගයේ මූලද්රව්ය පරමාණු සමග (උදාහරණයක් ලෙස, හයිඩ්රජන් පරමාණුවක් ඔක්සිජන් පරමාණුවක් සමඟ) ඉලෙක්ට්රෝන හුවමාරු කර ගැනීම නිසා ඒවා එකිනෙකට සම්බන්ද වේ. එයට රසායනික බන්ධන (chemical bonds) යන නම භාවිතා වෙනවා. මෙය හරියට ආදරය නමැති බන්ධනයෙන් කෙල්ලක් හා කොල්ලෙක් ළංව සිටිනවා වගේමයි. මෙලෙස බන්ධනය වී පවතින විට අප එයට අණුවක් (molecule) ලෙස පවසනවා. එනම්, හැම විටම අණුවක් යනු යම් රසායනික බන්ධනයකින් බැඳී තිබෙන පරමාණු කිහිපයකි. කෙල්ලක් හා කොල්ලෙක් ආදරයෙන් එක් තැන්ව සිටන විට, එම ඒකකයට පවුලක් කියා පවසනවා බදුය. ජලය යනු H හා O එකතු වී සෑදෙන එබදු අපට නැතිවම බැරි අණුවකි.
ලෝකයේ ඇති කෝටි ප්රකෝටි ගණනක් වූ විවිධ ද්රව්ය යනු ඇත්තටම මෙලෙස විවිධාකාරයෙන් සෑදුණු අණු බව දැන් ඔබට තේරුම් යා යුතුය. ජලය යනු ජල අණුවලින්ද, පොලිතින් යනු එතලින් යන අණුවලින්ද, ඩිස්ප්රින් (ඇස්පිරින්) යනු සැලිසිලික් ඇසිඩ් යන අණුවලින්ද සෑදී ඇත. එලෙසම අනෙක් සෑම ද්රව්යයක් ගැනමත් සිතිය හැකියි. පරමාණු ආකර්ෂණය වී බන්ධන සාදා අණු සෑදුවා සේම, අණු අතරද ආකර්ෂණ පවතිනවා. මෙම අණු අතර ඇතිවන ආකර්ෂණ නිසා තමයි ඝණ, ද්රව, වායු යන පදාර්ථයේ අවස්ථා තුන ඇති වන්නේ. අණු අතර ආකර්ෂණය ඉතා ඉහළ විට (strong bond), ඒවා ළඟින් ළඟින් පවතී. මෙය ඝණ අවස්ථාවයි. අණු මධ්යස්ථ ප්රමාණයෙන් ආකර්ෂණය (weak bond) වී පැවතීමෙන් ද්රවද, ඉතා දුර්වලව ආකර්ෂණය වී (no bond) පැවතීමෙන් වායුද ඇති වේ.
පිටතින් ශක්තිය (අලෝකය ලෙස, තාපය ලෙස, හෝ ඇතිල්ලීම, පීඩනය වැනි යාන්ත්රික ක්රමවලින්) ලබා දුන් විට මෙම සියලු ආකාරයේ බන්ධන දුර්වල වේ. ජලය යනු සාමාන්යයෙන් හෙවත් සාමාන්ය කාමර උෂ්ණත්වයේදී ද්රව මට්ටමේ පවතින දෙයක් බව ඔබ දන්නවා. ඊට තාපය ලබා දුන් විට, එය හුමාලය (water vapor) ලෙස හැඳින්වෙන වාත ස්වරූපයට පත්වන්නේ මෙනිසාය. තවද, ජලයෙන් ක්රමයෙන් තාපය ඉවත් කරමින් යන විට (හෙවත් සිසිල් කරන විට) එය අයිස් නමින් හැඳින්වෙන ඝණ තත්වයට පත්වන්නේද මෙය නිසාය. බවුතයෙන් රත් කරන විට ඝණ ඊයම් ද්රව වන්නේද මේ නිසාය. මේ ආකාරයට අනෙකුත් ද්රව්ය ගැනද සිතා බලන්න ඔබට දැන් පුලුවන්. ඝණයක් ද්රව වන උෂ්ණත්වය ද්රවාංකය (melting point) ලෙස හැඳින්වෙන අතර, විවිධ ද්රව්යවල මෙම උෂ්ණත්වය වෙනස් වේ. උදාහරණයක් ලෙස ජලයේ ද්රවාංකය සෙල්සියස් අංශක බින්දුව වන අතර, අප පෑස්සීමට ගන්නා සොල්ඩර්වල ද්රවාංකය 189 පමණ වේ. එලෙසම, යම් දියරයක් (ද්රවයක්) වායු බවට පත්වන උෂ්ණත්වය තාපාංකය (boiling point) වේ. උදාහරණයක් ලෙස ජලයේ තාපාංකය සෙල්සියස් අංශක 100 වේ.
පරමාණුවකට පිටතින් ශක්තිය ලබා දෙන විට, ඉහත කියූ ආකාරයට බන්ධන දුර්වල වන බවත්, අණු (හා පරමාණු) එකිනෙකට ඈත්වන බවත් පේනවා. ඒ විතරක් නොවේ, පරමාණුවලට පිටතින් ශක්තිය (තාපය) ලබා දුන් විට, එම පරමාණුවලින් ඉලෙක්ට්රෝනද ඉවත් වෙනවා (එනම්, උදාසීන පරමාණුව අයනයක් බවට පත් වෙනවා). පළමුව ඉවත්වන්නේ පිටතම ශක්ති මට්ටමේ ඇති ඉලෙක්ට්රෝන වේ. යම් පරමාණුවකින් මෙලෙස ඉලෙක්ට්රෝන ඉවත් කිරීම අයනීකරණය (ionization) ලෙස හැඳින් වෙන අතර, එලෙස ඉලෙක්ට්රෝනයක් ඉවත් කිරීමට පිටතින් ලබා දිය යුතු ශක්තිය අයනීකරණ ශක්තිය (ionization energy) ලෙස හැඳින් වෙනවා. පළමු ඉලෙක්ට්රෝනය ඉවත් කිරීමට වඩා වැඩි ශක්තියක් දෙවැනි ඉලෙක්ට්රෝනය ඉවත් කිරීමට යෙදීමට සිදු වෙනවා. දෙවැනි ඉලෙක්ට්රෝනය ඉවත් කිරීමට වැය කිරීමට සිදු වූ ශක්තියට වඩා වැඩි ශක්තියක් තුන්වෙනි ඉලෙක්ට්රෝනය ඉවත් කිරීමට අවශ්ය වෙනවා. මෙලෙස යම් පරමාණුවකින් ක්රම ක්රමයෙන් ඉලෙක්ට්රෝන ඉවත් කරන විට අයනීකරණ ශක්තියද ක්රමයෙන් වැඩිවන බව මින් පැහැදිලියි. කෙසේ හෝ වේවා, මෙලෙස යම් පරමාණුවක සියලු ඉලෙක්ට්රෝන ඉවත් කළ හැකියි. විවිධ මූලද්රව්යයන් සඳහාද අයනීකරණ ශක්තියද වෙනස් වෙනවා. උදාහරණයක් ලෙස, හයිඩ්රජන් පරමාණුවේ පළමු (හා එකම) ඉලෙක්ට්රෝනය ඉවත් කිරීමට අවශ්ය කරන අයණීකරණ ශක්තියට වඩා වෙනස් වූ ශක්ති ප්රමාණයක් කාබන් පරමාණුවක පළමු ඉලෙක්ට්රෝනය ඉවත් කිරීමට අවශ්ය වෙනවා. අධික ශක්තියක් පවතින පරිසරයකදී, පරමාණුවල සියලු ඉලෙක්ට්රෝන පරමාණුවලින් ඉවත් වී මෙලෙස අයන ලෙස පවතින අවස්ථා තිබෙන අතර, පදාර්ථය එලෙස පවතින විට, ප්ලාස්මා (plasma) යන නම ඊට අප භාවිතා කරනවා. ප්ලාස්මා යනු ඒ අනුව ඝන, ද්රව, වායු වලට අමතරව පදාර්ථය පැවතිය හැකි තවත් සුවිශේෂි අවස්ථාක් සේ සැලකෙනවා. තරුවල ඇත්තේ ඉතා ඉහළ උෂ්ණත්වයන් බැවින් ඒවායේ සියලු මූලද්රව්යයන් පවතින්නේ ප්ලාස්මා ස්වරූපයෙන්ය.
අපට ඉලෙක්ට්රොනික්ස්වලදී තඹ, යකඩ, ඇලුමිනියම්, රිදී ආදී ලෝහ වර්ග වැදගත්වන නිසා, විද්යාව අනුව ලෝහක් (metal) යනු කුමක්දැයි තේරුම්ගෙන සිටීම වැදගත්. මනුෂ්යකුගේ සාමාන්ය ශරීර උෂ්ණත්වය සෙල්සියස් අංශක 37ක් පමණය. සාමාන්යයෙන් කොළඹ වැනි ප්රදේශයක උෂ්ණත්වය අංශක 29 පමණ වේ. ෆ්රිජ් එකක් ඇතුළේ උෂ්ණත්වය බිංදුවට ආසන්නය. ඒ අනුව ෆ්රිජ් එකේ උෂ්ණත්වයට වඩා කොළඹ උෂ්ණත්වය වැඩිය. ඊටත් වඩා ශරීරයේ උෂ්ණත්වය වැඩිය. උෂ්ණත්වය (temperature) තිබෙන ඕනෑම තැනක තාප ශක්තිය (heat energy) ඇත. ඒ අනුව ෆ්රිජ් එක ඇතුළට වඩා කාමර උෂ්ණත්වය ඉහළ නිසා, සාමාන්ය කාමරය තුළ ශක්තිය වැඩිය. උෂ්ණත්වය අඩු වැඩි වීම මත තාප ශක්තියේ වෙනස්කම් ගැන එලෙස වැටහීමක් දැන් ඔබට ලබා ගත හැකියි. ලෝහ යනු යම් lattice යන නමින් හැඳින්වෙන යම් නිශ්චිත ආකාරයෙන් පරමාණු අතර බන්ධන සාදා ඇති ස්වරූපයක්ය.
එහෙත් කාමර උෂ්ණත්වය (එනම්, සාමාන්ය පරිසරයේ විසිරී තිබෙන තාප ශක්තිය) නිසා මෙම බන්ධනවල තිබෙන පරමාණු අයනීකරණයට ලක් වේ. එම “මුක්ත ඉලෙක්ට්රෝන” (free electrons) එම ලෝහය අත් හැර යන්නේ නැතිව, එම ලැටිස් ඔස්සේ නිදැල්ලේ එහෙ මෙහෙ සැරිසරයි. ලෝහයක් “ඉලෙක්ට්රෝන ජලාශයක” තිබෙනවා යනුවෙන් සමහරුන් මෙය හඳුන්වනවා.
මේ විදියට ගත්තහම, ලෝහයක නිදැල්නේ හැසිරෙන ඉලෙක්ට්රෝන ඕනෑ තරම් ඇත. විවිධ ලෝහවල විවිධ ප්රමාණවලින් මෙම ඉලෙක්ට්රෝන ඇත. අප විදුලියේදී යොදාගන්නේ මෙම නිදැල්ලේ පවතින ඉලෙක්ට්රෝනයි. එනම්, ලෝහ කැබැල්ලක් දෙපසට විදුලි පීඩනයක් (වෝල්ටියතාවක්) දුන් විට, එම ඉලෙක්ට්රෝන ඉතා පහසුවෙන් හා ක්ෂණයකින්, විදුලි පීඩනය වැඩි කෙළවරේ සිට අඩු කෙළවරට ගමන් කරන්නට පටන් ගන්නවා. මෙය විදුලි ධාරාවක් ලෙස අප හඳුන්වනවා.
ඉලෙක්ට්රෝන ගමන් කිරීමට අධිවේගි මාර්ග මෙන් ගමන් කිරීමට මාර්ග නැත. ඒවා ගමන් කරන විට, වංගු දදා යා යුතුය. තවද, අනෙක් ඉලෙක්ට්රෝනවලද හැප්පේ. මෙය හරියට සෙනඟ අධික (උත්සව කාලයක) පාරක ගමන් කරනවා බදුය.
මෙම හැප්පීම හෙවත් ඉලෙක්ට්රෝනවල ගමනට ඇතිවන බාධාව විදුලියේදී ප්රතිරෝධය ලෙස හඳුන්වන අතර, එම හැප්පීම නිසාම රත්වීමක්ද හට ගන්නවා. ඒ අනුව ප්රතිරෝධයක් තිබෙන හැම තැනම රත්වීමක්ද පවතින බව පෙනෙනවා. (ඔබේ අත්ල දෙක තදින් එකිනෙකට අතුල්ලන්න; ඉන් රස්නයක් ඉපදෙනු ඇත. කම්බියක් ගෙන එය යම් තැනකින් කැඩීමට වේගයෙන් දෙපසට නවන්න; එතැනද ගිනියම් වන තරමටම රස්නයක් ඇති වනු ඇත. ඕනැම දෙකක් ඇතිල්ලෙස හෝ එකිනෙකට ගැටෙන ස්ථානයක මෙලෙස තාපයක් උපදින බව සාමාන්ය එදිනෙදා ක්රියාකාරකම්වලින්ද අවබෝධ කර ගත හැකියි. එනිසා, ඉලෙක්ට්රෝන එකිනෙක ගැටෙන විටද, තාපයක් උපදී.) තවද, පහසුවෙන් ඉලෙක්ට්රෝන ගමන් කරන (හෙවත් හොඳ විද්යුත් සන්නායක) ලෝහවලට තාපයද පහසුවෙන් ගමන් කරවිය හැකියි. යම් ඉලෙක්ට්රෝනයක් රත් වී ඇතැයි සිතන්න. ඉලෙක්ට්රෝනවලට ශක්තිය ලැබුණ විට එයකම්පනය වීම (vibration) අධික වෙනවා (හරියට මත්වතුර බී විට, මිනිසුන් පිස්සු විකාර කරමින් දඟලනවා බදුය). ලෝහය තුළ ඉලෙක්ට්රෝන එහා මෙහා යන නිසා, එම රත් වූ ඉලෙක්ට්රෝන වෙනත් ඉලෙක්ට්රෝනවලට ස්පර්ශවීමෙන් එම ඉලෙක්ට්රෝනයෙ රස්නයෙන් කොටසක් අනෙක් ඉලෙක්ට්රෝනවලට ගමන් කරනවා. මේ ආකාරයට පහසුවෙන් තාපය ගමන් කරනවා. මේ අනුව විදුලි හා තාප පරිවාරක ද්රව්යයක් කෙසේ විය යුතුදැයි ඔබට සිතා ගත හැකි විය යුතුයි (විදුලි හා තාප පරිවාරක තුළ එහා මෙහා යන නිදහස් ඉලෙක්ට්රෝන නොතිබිය යුතු බව).
ලෝහ රත් වන විට, එහි ප්රතිරෝධිතාව වැඩි වේ. ඊටද හේතුව මේ විදියටම තර්ක කළ හැකියි. රත්වීම වැඩි වන විට, ඉලෙක්ට්රෝන දැනටමත් අධිකව තිබෙන තැනක ඉලෙක්ට්රෝන කම්පනය වැඩිවීම හේතුවෙන් ඉලෙක්ට්රෝන වැඩි වැඩියෙන් එකිනෙකාගේ “ඇඟේ හැප්පෙනවා”. එනම්, ප්රතිරෝධය වැඩි වෙනවා. එහෙත් අර්ධ සන්නායක හා පරිවාරකවලට මෙය වෙනස් විදියකටයි බලපාන්නේ. රත් වීමෙන් (එනම් ශක්තිය වැඩි වීමෙන්) එම ද්රව්යවල ඉලෙක්ට්රෝන වැඩි වැඩියෙන් ඉවත් වෙනවා. එනම්, නිදහස් ඉලෙක්ට්රෝන ගණන වැඩි වෙනවා. ඉලෙක්ට්රෝන හිඟ තැනක නිදහස් ඉලෙක්ට්රෝන වැඩිවන විට, එහි සන්නායක ගුණය වැඩි වෙනවා. මෙම කාරණා හොඳින් සිහි තබා ගත්තොත් ඔබට පසුවට ට්රාන්සිස්ටර් වැනි පාඩම් තේරුම් ගැනීමට ඉවහල් වේ.
ඉහත ආකාරයට පදාර්ථ ගැන යම් පමණකට දැනගත් අප දැන් ශක්තිය පිළිබඳවද කෙටියෙන් සලකා බලමු. ශක්තිය යනු “යම් කාර්යක් කිරීමේ හැකියාව” ලෙස අර්ථ දැක්වේ. එමනිසා පදාර්ථ මෙන් මේවා අතින් ඇල්ලීමට බැරිය. එනම්, ශක්තින් පදාර්ථ මෙන් අවකාශයේ යම් ඉඩක් ගන්නේ නැති අතර, ස්කන්ධයක්ද නැත්තේය. එහෙත් ශක්තින් ක්රියාකරන්නේ පදාර්ථ මතය. පදාර්ථ (පරමාණු) මත ශක්තිය ක්රියා කිරීමෙන් එම පදාර්ථ (පරමාණු) වලට යම් යම් භෞතික වෙනස්කම් ඇති වේ. එවැනි වෙනස්කම් කිහිපයක් නම්, පදාර්ථයේ හැඩය වෙනස් වීම හෝ ප්රසාරණය වීම හෝ හැකිලීම (උදාහරණයක් ලෙස, රබර් රත් කරන විට එහි හැඩය වෙනස් වේ.), පදාර්ථයේ අවස්ථාව වෙනස් වීම (උදා: බටර් රත් කරන විට එය ද්රව වේ.), හෝ ගතිගුණ වෙනස් වීම (උදා: කොලයක් රත් කරන විට එය අඟුරු බවට පත් වේ.), චලනයක් සිදු වීම වේ.
සියලු පදාර්ථයන්ට මුල/හේතුව මූලද්රව්යවලින් (එනම්, පදාර්ථ සෑදී ඇත්තේ මූලද්රව්යවලිනි) සේම සියලු ශක්තීන්ට මුල බලය (force) වේ. එනම්, ඕනෑම ශක්තියක් පිටුපස යම්කිසි බලයක් ඇත. නූතන විද්යාව අනුව, එවැනි එකිනෙකට වෙනස් බල ඇත්තේ හතරක් පමණි. ඒවා, ගුරුත්වය හෙවත් ගුරුත්වාකර්ෂණ බලය (gravity or gravitational force), විද්යුත් චුම්භක බලය (electromagnetic force), ප්රබල න්යෂ්ඨික බලය (strong nuclear force), හා දුබල න්යෂ්ඨික බලය (weak nuclear force) වේ.
මින් ගුරුත්වාකර්ෂණය ගැන අපට හොඳ වැටහීමක් තිබෙනවා. ඕනෑම පදාර්ථ දෙකක් අතර එම දෙක එකිනෙකා ආකර්ෂණය කිරීම මින් සිදු වේ. උඩ පැන්න විට බිමට වැටෙන්නේ ඔබ (එක් පදාර්ථයක්) පොලොවෙන් (තවත් පදාර්ථයක්) ඈත් වූ විට, ඒ දෙක එකිනෙකාව ආකර්ෂණය කිරීමේ හේතුව නිසාය. මෙහි විශේෂත්වය වන්නේ ගුරුත්ව විකර්ෂණය (එනම්, එකිනෙකාව විකර්ෂණය කරන) කියා දෙයක් නොමැති වීමයි. (එහෙත් සමහර පර්යේෂකයන් එවැනි ගුරුත්ව විකර්ෂණයක් සොයා ගැනීමට උත්සහ කරනවා. ඇත්තටම මෙයට ගුරුත්ව විකර්ෂණය නොකියා කවුරුත් භාවිතා කරන වචනය වන්නේ ප්රතිගුරුත්වය (antigravity) කියාය.)
ඉලෙක්ට්රොනික්ස්වලදී වැඩිපුරම වැදගත්වන බලය වන්නේ විද්යුත් චුම්භක බලයයි. විදුලි ශක්තිය, චුම්භක ශක්තිය, ආලෝකය, රේඩියෝ තරංග, x කිරණ, ගැමා කිරණ, තාපය, හා සෑම රසායනික ශක්තියක්ම පිටුපස සිටින්නේ මෙම බලයයි. කලකට ඉහතදී චුම්භක බලය හා විද්යුත් බලය ලෙස වෙන වෙනම දෙකක් ලෙස සලකනු ලැබුවත්, මේ දෙකම එකම ශක්තියක ප්රභේද (ආකාර) දෙකක් බව පසුව සොයා ගත්තා. එතැන් සිට, මේ දෙකම විද්යුත් චුම්භක (electromagnetic – EM) බලය යනුවෙන් තනි බලයක් ලෙස සැලකෙන්නට පටන් ගත්තා.
ප්රබල හා දුබල න්යෂ්ඨික බල ගැන අපට එතරම් වැදගත් නැත. ඒවා සමග වැඩ කටයුතු කරන්නට උසස් දැනුමක් සේම උසස් විද්යාගාර පහසුකම් අවශ්ය කෙරෙනවා. පරමාණුවක න්යෂ්ඨිය ඉතාම කුඩා නිසා ඒ තුළ ප්රෝටෝන හා නියුට්රෝන ඉතා ළඟින් ඇහිරී තිබෙන්නේ ප්රබල න්යෂ්ඨික බලය හේතුවෙනි. එම බලය න්යෂ්ඨියෙන් පිටතට දැනෙන් නැත. එහෙත්, න්යෂ්ඨියක් දෙකඩ කිරීමකදී හෝ කුඩා න්යෂ්ඨි දෙකක් එකතු කිරීමේදීද මෙම බලයෙන් කොටසක් පිටතට ගත හැකියි. න්යෂ්ඨික බෝම්බ හා බලාගාරවල සිදු කරන්නේ මෙයයි (එනම් න්යෂ්ඨි කැඩීම (nuclear fission) හෝ න්යෂ්ඨි එකතු කිරීම (nuclear fusion) වේ.) දුබල න්යෂ්ඨික බලයෙන් එතරම් ප්රයෝජනයක් අපට නැත. විකිරණශීලී (radioactive) මූලද්රව්ය ලෙස හැඳින්වෙන මූලද්රව්යවලින් විකිරණ (radiation) පිටවෙන්නේ මෙම දුබල න්යෂ්ඨික බලය ක්රියාකාරී වීමෙනි.
විකිරණශීලිතාව (radioactivity) යනු සරල දෙයකි. යම් මූලද්රව්ය පරමාණුවක න්යෂ්ඨියට බලපෑම් කිරීම (එනම්, එය කැඩීම හෝ ඊට තවත් නියුට්රෝන හෝ ප්රෝටෝන එකතු කිරීම) ඉතාම අපහසුය. එහෙත් සමහර මූලද්රව්යවල යම් යම් සමස්ථානික තිබෙනවා ඉතා අස්ථාවර න්යෂ්ඨි සහිත. එනම්, එම සමස්ථානිකවල න්යෂ්ඨි ස්ථාවර වන්නට උත්සහ කරනවා තම න්යෂ්ඨියෙන් ප්රෝටෝන හා නියුට්රෝන යම් ගණනක් එලියට විසි කිරීමෙන්. (මෙය න්යෂ්ඨිය කැඩී යෑමක් සේ සැලකෙනවා.) මෙය හරියට බර වැඩි නිසා ගිලෙන්නට යන නැවකින් එම නැවේ බඩු එලියට විසි කරනවා වගේ දෙයකි. මෙම ඉබේම සිදුවන න්යෂ්ඨිය කැඩී යෑම තමයි විකිරණශීලිතාව ලෙස හඳුන්වන්නේ. (න්යෂ්ඨියෙන් ප්රෝටෝන ඉවත් වන විට ඔබට දැන් තේරෙනවා ඉබේම එම මූලද්රව්යයේ නමත් වෙනස් විය යුතුයි කියලා.) මෙලෙස න්යෂ්ඨි කැඩී යෑමේදී ප්රෝටෝන, නියුට්රෝන, ඉලෙක්ට්රෝන මෙන්ම යම් විද්යුත් චුම්භක කිරණද වේගයෙන් ඉවත් වෙනවා. මෙම ඉතා වේගයෙන් ඉවත් වන දේවල්වලට තමයි විකිරණ කියලා කියන්නේ. එම විකිරණ යම් යම් ද්රව්ය මත හැප්පුනාම එම ද්රව්යවලට හානි සිදු වෙනවා. එනම්, එම ද්රව්ය සෑදී ඇති පරමාණුවලින් ඉලෙක්ට්රෝන ගැලවී විසි වෙනවා (එනම්, අයනීකරණය සිදු වෙනවා) මෙම වේගවත් විකිරණ වැදීමෙන්. ජීවියෙකුගේ ශරීරයට මෙවැනි දෙයක් සිදුවන විට, එම ජීවි කොටස් හානි වීමෙන් පිළිකා ආදී රෝගද මරණයද ඇති කළ හැකියි. එමනිසයි, විකිරණ ඉතා මාරාන්තික වන්නේ.
අවසන් වශයෙන් ශක්තිය ගැන කිව යුත්තේ ශක්තිය අපට දැනගත හැක්කේ ඒවා පදාර්ථ මත ක්රියාකාරී වීමේන් එම පදාර්ථයන්හි ඇතිවන වෙනස්කම් ඔස්සේ බවයි. මේ විශ්වයේ සිදුවන සෑම ලොකු කුඩා සිදුවීමක්ම සිදු වන්නේ පදාර්ථ හා ශක්ති යන දෙකෙහි විවිධාකාරයේ අන්තර්ක්රියාකාරිත්වයන් (interactivity) නිසාය.
විද්යාවේ මූලික කාර්යක් තමයි විවිධාකාරයේ දේවල් මැනීම (measure). මෙම මැනීම සඳහා විශ්වාසදායි උපකරණ භාවිතා කරනවා. ලබා ගන්නා මිනුමේ නිරවද්යතාව එය මනින විදිය සේම එය මැනීමට භාවිතා කරන උපකරණය මතද රඳා පවතිනවා. මැනිය හැකි දේවල් රාශි (quantity) හෙවත් මාන (dimension) ලෙස හැඳින් වේ. මූලික රාශින් ඇත්තේ අටක් පමණ වන අතර අනෙක් දහස් ගණනක් වූ රාශින් ඇත්තටම අප මෙම මූලික රාශී අනුසාරයෙන් ගොඩ නගා ගන්නවා (ව්යුත්පන්න කරනවා). මෙයද විද්යාවේ ජයග්රහණයකි. කෝටි ගණනක් වූ සියලුම පදාර්ථ මූලද්රව්ය එකසිය ගණනකින්ද, දුසිම් ගණනක් වූ සියලුම ශක්තින් මූලික බල හතරකින්ද අවබෝධ කර ගත හැකි සේම, දහස් සංඛ්යාත විවිධ රාශීන් සියල්ල මූලික රාශි අටකින් පමණ අවබෝධ කර ගැනීමට පුලුවන්. විද්යාවේ මෙම මූලික අංග දන්නා අයට අති විශාල ලෝකය පිළිබඳ අති විශාල අවබෝධයක් ලබා ගත හැක්කේ මේ නිසාය. මෙම මූලික රාශින් වන්නේ, ස්කන්ධය (mass), දුර/දිග (length), කාලය (time), උෂ්ණත්වය (temperature), “ද්රව්ය ප්රමාණය මනින” මවුලය (mole), ධාරාව (current), ආලෝක ත්රීව්රතාව (light intensity), කෝණ(angle) වේ.
මේ එක් එක් රාශිය මැනීමට යම් යම් ඒකක සම්මත කර ගෙන ඇත. අද ලොවපුරා කවුරුත් භාවිතා කරන සම්මතය වන්නේ SI ඒකකයි. එහෙත් මෙම එස්අයි ඒකක භාවිතා කිරීමට පෙරද විවිධ රටවල් විවිධ ඒකක භාවිතා කර තිබුණා. එමනිසා, එවැනි ඒකක අදද භාවිතා වෙනවා. මා පහත රාශි කිහිපයක් ගැන කෙටියෙන් විස්තර කරනවා ඒවායේ එස්අයි හා අනෙකුත් ප්රචලිත ඒකක සමග. සෑම ඒකකයකටම කෙටි සංඛේත නාමයක්ද ඇත. තවද, මේ සෑම රාශියක්ම එහි සාමාන්ය දිග නමින් ලිවීම කරදරයි නිසා, ඒ සෑම රාශියක් සඳහාම කෙටි සංඛේත නාමයකුත් ලබා දී තිබෙනවා. උදාහරණ ලෙස, දිග යන්න L වලින්ද, කෝණික ප්රවේගය ω වලින්ද ආදී ලෙස ඒවා ලියා දක්වනවා. මා එම සෑම කෙටි කේත නාමයක්ම රාශියේ දිග නාමයට පසුම කොමාවක් යොදා ලියා දක්වනවා (උදාහරණ ලෙස “දිග, L” ).
ස්කන්ධය, M මනින සම්මත ඒකකය කිලෝග්රෑම් (kilogram) වේ. (කෙටි සංඛේතය kg වේ.) ස්කන්ධය මනින තවත් ප්රචලිත ඒකක කිහිපයක් හා ඒවා එකිනෙකට ඇති අනුපාතද පහත දැක්වේ. පහත දැක්වෙන මෙට්රික් ටොන් එකෙහි මෙට්රික් යන කොටස අත් හැර නිකංම ටොන් කියා කියන්නට පුරුදු වෙන්න එපා. මෙට්රික් ටොන් එකට අමතරව වෙනත් ටොන් (long ton, short ton ලෙස) ඇත.
1000 kg = 1 metric ton (මෙට්රික් ටොන්)1000 g (ග්රෑම්) = 1 kg
1 kg = 0.45 lb (pounds - රාත්තල්)1 lb = 16 oz (ounce - අවුන්ස)
1 oz = 16 dr (dram - ඩ්රෑම්)
1 oz = 28 g
1 g = 5 car (carat - කැරට්)
1 kg = 0.45 lb (pounds - රාත්තල්)1 lb = 16 oz (ounce - අවුන්ස)
1 oz = 16 dr (dram - ඩ්රෑම්)
1 oz = 28 g
1 g = 5 car (carat - කැරට්)
යම් කිසි දුර ප්රමාණයක් හෙවත් දිග, L මැනීමට සම්මත ඒකකය මීටරය (meter) (m) වේ.
1 yd (yard - යාර) = 3 ft (feet - අඩි)1 ft = 12 in (inches - අඟල්)1000 milli (මිලි) = 1 in (අඟලින් දහාකින් එක් පංගුවක් මිලි එකකි.)
1 f (fathom - බඹ) = 6 ft
1 mi (mile - සැතැප්ම) = 5280 ft = 1.6 km
1 A (Angstrom - ඇංස්ට්රම්) = 10-10m
1 micron = 1 micrometer
1 f (fathom - බඹ) = 6 ft
1 mi (mile - සැතැප්ම) = 5280 ft = 1.6 km
1 A (Angstrom - ඇංස්ට්රම්) = 10-10m
1 micron = 1 micrometer
අලෝක වර්ෂය (light year) යනුවෙන් ඉතා විශාල දුරවල් මැනීමට (තාරකා විද්යාවේදී නිතර භාවිතා වන) යොදාගන්නා ඒකකයක්ද ඇත. මෙහි තේරුම සරලය. ආලෝකය ගමන් කරන්නේ නියත නිශ්චිත වේගයකින්ය (එයතත්පරයට කිලෝමීටර් 300,000 ක වේගයකින්). එම වේගයෙන් එක වසරක් තුළ ආලෝක කිරණයක් ගමන් ගත්තේ නම්, එය ගමන්ගත් මුලු දුරට සමාන දුරක් ආලෝක වර්ෂය ලෙස හැඳින් වේ. අප එය දළ වශයෙන් ගණනය කරමු. (ආලෝකයේ වේගය 60න් වැඩි කර එය තත්පර 60කදී හෙවත් විනාඩියකදී ගමන් කරන දුර ලබා ගෙන, නැවත එය 60න් වැඩි කර පැයක කාලයක් තුළ ගමන් කරන දුර සොයාගෙන, නැවත එය 24න් වැඩි කර දවසක කාලයක් තුළ ගමන් කරන දුර සොයා ගෙන, නැවතත් 365න් වැඩි කර වසරකට යන දුර සොයාගත හැකියි.)
ආලෝක වර්ෂ 1 = 300,000 x 60 x 60 x 24 x 365 = 9,460,800,000,000 km
අඩිය හා අඟල දැක්වීමට තවත් ප්රචලිත සංඛේත ක්රමයක්ද ඇත. යම් අගයකට පසුව ඉහළින් ඉරි කැබැල්ලක් (prime) ගැසූ විට ඉන් අඩිද, එලෙස ඉරි කැබැලි දෙකක් (double primes) ගැසූ විට අඟලද ඉන් හැඟ වේ.
5’ = අඩි 5
3’’ = අඟල් 3
4’ 7’’ = අඩි 4යි අඟල් 7යි.
3’’ = අඟල් 3
4’ 7’’ = අඩි 4යි අඟල් 7යි.
කාලය, T මනින සම්මත ඒකකය තත්පර (second) (s) වේ.
60 s = 1 min (minutes - මිනිත්තු)60 min = 1 hr (hour - පැය)1 yr (year - අවුරුද්ද) = 54 wk (weeks - සති)
උෂ්ණත්වය, Temp මනින සම්මත ඒකකය කෙල්වින් (Kelvin) (K) වේ. විශ්වයේ තිබිය හැකි අවම උෂ්ණත්වය ලෙස විද්යාව විසින් සොයා ගෙන ඇත්තේ සෙල්සියස් අංශක ඍණ 273.15 පමණය. මෙම උෂ්ණත්වය කෙල්වින් 0 ලෙස දැක්වේ. කෙල්වින් උෂ්ණත්වය හා සෙල්සියස් උෂ්ණත්වය අතර පහසුවෙන් අගයන් පරිවර්ථනය කළ හැකියි. යම් කෙල්වින් උෂ්ණත්වයක් සෙල්සියස් වලට පෙරළීමට කළ යුත්තේ -273 ක් එකතු කිරීම පමණයි (දශම කොටස නොසලකා හැරිය හැකිය). සෙල්සියස් (Celsius) යන්නටමයි සෙන්ටිග්රේඩ් (centigrade) කියා කියන්නෙත්.
0 K = -273.15 oC (Celsius degree - සෙල්සියස් අංශක) නිසා,
“x” + 273 oC = “x” K
x oC = 32 + (7/5)x oF (Fahrenheit degree - ෆැරන්හයිට් අංශක)
“x” + 273 oC = “x” K
x oC = 32 + (7/5)x oF (Fahrenheit degree - ෆැරන්හයිට් අංශක)
පොලොව සාමාන්යයෙන් එක සමාන සුමට ස්වභාවයක් නොගනී. එහි කඳු හා හෙල් වැනි ස්වභාවයන් පවතී. එමනිසා, පොලොව මට්ටම ලෙස සැලකිය යුත්තේ කුමක්දැයි ප්රශ්නයක් පැන නගී. එය විසඳාගෙන ඇත්තේ ලොව ඕනෑම තැනක මුහුදු වෙරළ මට්ටම එම භූමියේ පොලෝ මට්ටම ලෙස සැලකිය යුතු යැයි සම්මත කරගැනීමෙනි. එය මුහුදු මට්ටම (sea level) ලෙස ව්යවහාර වේ. පොලොවේ සිට ඉහළට ඇති උස හැමවිටම වාගේ විද්යාව තුළ ගණනය කරන්නේ මෙම මුහුදු මට්ටමේ සිටයි. මෙලෙස මුහුදු මට්ටමේ සිට ඉහළට ඇති උසට ඉංග්රීසියෙන් altitude කියා කියනවා. මෙම ඇල්ඩිටියුඩ් එක අනුවද උෂ්ණත්වය වෙනස් වෙනවා. එනම්, ඇල්ටිඩියුඩ් එක වැඩි වන සෑම මීටර් 100 කටම උෂ්ණත්වය 0.64 බැගින් අඩු වෙනවා. ඒ අනුව, පොලොවේ සිට 10km ක් උසකදී උෂ්ණත්වය සෙල්සියස් අංශක 64 කින් මුහුදු මට්ටමේ උෂ්ණත්වයට වඩා අඩුය. උදාහරණයක් ලෙස, කොළඹ අවට මුහුදු මට්ටමේ උෂ්ණත්වය අංශක 28 නම්, එම ප්රදේශයට 10km ක් උඩින් අහසේ උෂ්ණත්වය (28 – 64 =) -36 කි. (මේ අනුව, ඔබ ඔලුව උස්සා අහස බලන විට ඔබට උතුරු හෝ දකුණු ධ්රැවවල පවතින දැඩි සීතල සහිත ප්රදේශයක් වැනි පෙදෙසක් පෙනෙන තෙක් මානයේම තිබේ.)
සලකා බලන ද්රව්යය හාල් හැට, වැලි කැට වැනි එකින් එක ගත හැකි ආකාරයෙන් පවතී නම්, අපට එම ද්රව්යයේ අච්චර ඇට/කැට ප්රමාණයක් තිබෙනවා යැයිද ගණනය කළ හැකිය. හාල්, වැලි, සීනි වැනි ද්රව්ය අප එසේ එකින් එක ගණන් කරන්නට යන්නේ නැති වුවත්, පරමාණු හා අණු එලෙස ගණන් කළ හැකියි. (ඇත්තටම මෙහිදීද එකින් එක අංශු ගණන් කරන්නේ නැති අතර, වක්ර ක්රමවලින් එය සිදු කෙරේ.) එලෙස අංශු ගණන් කරන විට, අංශු6.023 x 1023 ක විශාල අංශු ගණනක් ඇති විට එතැන එම අංශු මවුලයක් තිබේ යැයි කියනවා. මෙම සංඛ්යාව ඇවගාඩ්රෝ සංඛ්යාව හෝ ඇවගාඩ්රෝ නියතය (Avagadro constant) ලෙස හැඳින් වෙන අතර, රසායන විද්යාවට මෙම මවුල භාවිතා කර ගණනය කිරීම ඉතාම වැදගත්ය. (එනම්, යම් යම් රසායන එකිනෙකට මිශ්ර කරන අනුපාත සාදා ගන්නේ මෙම මවුල නම් ඒකකය භාවිතා කරමින්ය. පහත මා කෙටියෙන් පරමාණුවල හා අණුවල මවුල ප්රමාණයන් සකස් කර ගන්නා අයුරු විස්තර කරනවා. වැඩි විස්තර සඳහා රසායන විද්යාව ගැන ඉගෙන ගන්න.)
ඕනෑම රසායනිකයක් සෑදී ඇත්තේ එම රසායනිකයේ ගුණ පෙන්වන අණුවලින් බව පෙර අප සඳහන් කළා. ඒ අනුව ජලය සෑදී තිබෙන්නේ ජල අණුවලිනි. (අණු සෑදී තිබෙන්නේ පරමාණුවලින් බවද ඔබ දන්නවා. උදාහරණයක් ලෙස ජල අණුව සෑදී තිබෙන්නේ ඔක්සිජන් එක් පරමාණුවකට හයිඩ්රජන් පරමාණු දෙකක් බන්ධනය වීමෙනි.) (මෙහි හයිඩ්රජන් හා ඹක්සිජන් පරමාණු දෙක අතර දුර ඇංස්ට්රම් ඒකකයෙන් හා හයිඩ්රජන් පරමාණු දෙක ඔක්සිජන් කේන්ද්ර කරගෙන සාදන කෝණය අංශක වලින්ද පෙන්වා ඇත.)
එක් එක් පරමාණුවක ස්කන්ධය හෙවත් පරමාණුක ස්කන්ධය අප දන්නවා (එය දළ වශයෙන් අප සලකා බලන පරමාණුවේ නියුක්ලියෝන ගණන ලෙස සැලකිය හැකියි. ඉතා නිවැරදිම අගය සාදා ගන්නේ ඊට වඩා තරමක් වෙනස් ආකාරයකින් වන අතර, එම නිවැරදි අගයන්ද වගුවල සඳහන් වේ). යම් පරමාණුවක් සලකා බැලුවොත් එම පරමාණුවේ පරමාණුක ස්කන්ධයට සමාන ග්රෑම් ගණනක් මැනගත් විට, එහි පරමාණු ඇවගාඩ්රෝ සංඛ්යාවක් තිබේ යැය සොයා ගෙන තිබෙනවා. මෙය විස්මිත සොයා ගැනීමකි. ඇවගාඩ්රෝ නම් විද්යාඥයා විසින් එය සොයාගත් නිසා ඔහුගේ නමින්ම එම නියතය නම් කර ඇත. උදාහරණ කිහිපයක් ගමු. හයිඩ්රජන්වල පරමාණුක ස්කන්ධය1 වේ. එවිට, හයිඩ්රජන් පරමාණු ග්රෑම් එකක් (1 g) කිරාගත් විට, එතැන H මවුල එකක් හෙවත් H පරමාණු ඇවගාඩ්රෝ සංඛ්යාවක් තිබෙනවා. ක්ලෝරින්වල පරමාණුක ස්කන්ධය 35.5 වේ. ඒ අනුව Cl පරමාණුවලින් 35.5 gක් කිරාගත් විට අපට Cl මවුල එකක් ලැබෙනවා.
එවිතරක්ද නොවේ. පරමාණුවකට පරමාණුක ස්කන්ධය තිබෙන්නාක් සේ අණුවකට අණුක ස්කන්ධයක් ඇත. යම් අණුවක ස්කන්ධය හෙවත් අණුක ස්කන්ධය (molecular mass) අපට පහසුවෙන්ම ගණනය කරගන්න පුලුවන් එම අණුව සෑදී තිබෙන පරමාණු දන්නවා නම්. කළ යුත්තේ එම අණුවේ පරමාණු සෑම එකකම පරමාණුක ස්කන්ධ එකතු කිරීම පමණි. එලෙස අප උදාහරණයක් ලෙස ජල අණුවක අණුක ස්කන්ධය ගණනය කරමු.
ජල අණුවේ අණුක ස්කන්ධය මේ අනුව (2 x 1) + 18 = 20 වේ.
යම් අණුවක එහි අණුක ස්කන්ධයට සමාන ග්රෑම් ගණනක් කිරාගත් විට, එතැන එම අණුවේ මවුලයක් තිබේ. ඒ අනුව, උදාහරණයක් ලෙස, ජල අණුවලින් 20 g ක් කිරාගත් විට, එතැන ජල අණු ඇවගාඩ්රෝ සංඛ්යාවක් හෙවත් ජල අණු මවුලයක් තිබෙනවා. ජල අණුවලින් 10 g ක් කිරාගත් විට එතැන ඇත්තේ මවුල භාගයක් පමණි. මෙලෙස ඕනෑම රසායනිකයක අපට අවශ්ය ඕනෑම මවුල ගණනක් සාදා ගත හැකියි.
ආලෝකය ගැන වෙනමම පාඩමක් ඉදිරියෙදී හමුවන බැවින් ආලෝක ත්රීව්රතාව ගැන මෙහිදී සලකා බලන්නේ නැත. ධාරාව පිළිබඳ මෙම පොතේම සාමාන්ය පාඩම් යටතේම විස්තර කර ඇත. අප කෝණ, θ සාමාන්යයෙන් මනින්නට පුරුදුව ඇත්තේ අංශක (degree) වලින්ය. යම් ලක්ෂයක් වටා වෘත්තයක් ඇන්ද විට, එම වෘත්ත පථයෙන් එම මධ්ය ලක්ෂය හෙවත් කේන්ද්රයට ඇති කරන (ආපාතනය කරන) සම්පූර්ණ කෝණය අංශක 360 ලෙස අර්ථ දක්වා ඇත.
ඒ අනුව අර්ධවෘත්තයක අංශක 180ක් ඇත. යම් රේඛා දෙකක් පහත රූපයේ දැක්වෙන ආකාරයට අංශක 90ක් තිබෙන සේ ඇති විට, එය ලම්භක (perpendicular) ලෙස නම් කෙරේ.
එක් අංශකයක් 60කට බෙදූ විට, ඉන් එක කුඩා කොටසක් කලා (minute) එකක් ලෙසද, එක කලාවක් නැවත කුඩා කෝණ 60කට බෙදූ විට, ඉන් එක කොටසක් විකලා (second) එකක් ලෙසද හැඳින් වේ.
1o = 60’ (මෙලෙස අංශකයක් ඉහළට එසවූ කුඩා බිංදුවකින්ද, කලාව උඩු කොමාවක් මගින්ද සංඛේතවත් වේ.)1’ = 60’’ (විකලාව සංඛේතවත් කෙරෙන්නේ උඩු කොමා දෙකක් යෙදීමෙනි.)
සාමාන්යයෙන් කෝණ ඉහත ක්රමවලින් මැනීමට පුරුදුව සිටියත් කෝණ මනින සම්මත ඒකකය එය නොවේ. එස්අයි ඒකකය රේඩියන් (radian) ලෙස හැඳින් වේ. යම් වෘත්තයක එහි අරයට සමාන දිගක් එම වෘත්තයේම පරිධිය ඔස්සේ මැනගත් විට, එහි දෙකෙළවරින් (එනම් එම පරිධියේ කොටස විසින්) කේන්ද්රයේ ආපාතනය කරන යම් කෝණයක් වේද එය රේඩියන් එකක් ලෙස අර්ථ දක්වා ඇත.
මේ අනුව ඕනෑම වෘත්තයක කේන්ද්රය වටා ආපාතනය කරන සම්පූර්ණ රේඩියන් කෝණය 2π වේ. (π යනු නියතයක් වන අතර එයි අගය 3.1412 වේ. පාසල් පොත්වල මෙය 22/7 ලෙසද දකවා තිබේ. මෙම අක්ෂරය ග්රීක හෝඩියේ අකුරක් වන අතර එය නියම ලෙස ශබ්ද කළ යුත්තේ “පයි” කියා මිස “ෆයි” කියා නොව. “ෆයි” යනුවෙන් වෙනත් ග්රීක අකුරක් ඇති අතර එය ලියන්නේ φ ලෙසය. විද්යාවේදී හා ගණිතයේදී අප ග්රීක හෝඩියේ බොහෝ අකුරු නිතර භාවිතා කරන බව මතක තබා ගන්න. α (ඇල්ෆා), β (බීටා), ε (එප්සිලෝන්), η (ඊටා), θ (තීටා), λ (ලැම්ඩා), μ (මියු), ρ (රෝ), σ (සිම්පල් සිග්මා), Σ (කැපිටල් සිග්මා), δ (සිම්පල් ඩෙල්ටා), Δ (කැපිටල් ඩෙල්ටා), ω(ඔමෙගා) යන අක්ෂර ඔබ නිතර දැක ඇතිවාට සැකයක් නැත.)
මෙම කෝණ යම් මතුපිටක් මත හෙවත් තලයක ඇති කෝණ නිසා තල කෝණ (plane angle) ලෙස හැඳින් වේ. ඝන කෝණ (solid angle), Ω ලෙසද කෝණ පවතී. එය මනින සම්මත ඒකකය ස්ටෙරඩියන් (steradian) වේ. ඝන කෝණයක් යනු යම් “මුල්ලක්” වැනි කොටසකින් ඇති කරන ත්රිමාණ කෝණයකි. පහත රූපය බලන්න. මෙම A යනුවෙන් දක්වා ඇති මතුපිටෙහි වර්ගඵලය එම ගෝලයේ අරයෙහි වර්ගයට (එනම්, r2) සමාන විට, ස්ටෙරඩියන් එකක ඝන කෝණයක් යැයි අර්ථ දක්වා තිබෙනවා. මෙය ඔබට තරමක් නුහුරු වන්න පුලුවන් මුලදී මොකද තල කෝණ නිතර කුඩා කළ සිටම භාවිතා කළත් ඝන කෝණ අප උසස් ගණිතය හදාරන තුරු ඉගෙන ගන්නේ නැති නිසා. එහෙත් ඝන කෝණ යනු තල කෝණය මෙන්ම ඉතාම සරල දෙයකි. ඝන කෝණයක් ත්රිමාන කෝණයක් නිසා, එය සිතිය යුත්තේ දෙවන රූපයෙන් පෙන්වා තිබෙන පරිදි පුනීලයක මුල්ලක් සේය.
මෙම කෝණ පුනීලයක උල් කෙළවර වැන්නක හැඩය ගනී. තල කෝණයක සම්පූර්ණ කෝණය ගත් විට ඇඳෙන්නේ වෘත්තයක් වුවද, ඝන කෝණයක සම්පූර්ණ කෝණය ගත් විට අපට ලැබෙන්නේ ගෝලයකි (sphere). ඉහත පළමු රූපයෙන් එය පැහැදිලි වේ. ඕනෑම ගෝලයක මතුපිටින් (ගෝලයක මතුපිට යන්න වෘත්තයක පරිදියට අනුරූප වේ.) ගෝලයේ කේන්ද්රය මත ආපාතනය කරන සම්පූර්ණ ඝන කෝණය ස්ටෙරඩියන් 4π වේ.
ඉහත සියලු එස්අයි ඒකක අපට අවශ්ය පරිදි කුඩා හා විශාල කළ හැකි ක්රමයක් විද්යාව විසින් හඳුන්වා දී තිබෙනවා. මෙමගින් යමක් මැනීමට යම් ඒකකයක් විශාල වැඩි හෝ කුඩා වැඩි නම්, ඒ සඳහා තවත් විවිධ වර්ගයේ ඒකක රොත්තක් හඳුන්වා දෙන්නේ නැතිව ඉතා ක්රමවත් ආකාරකට එය කරගැනීමේ හැකියාව මින් ලැබී ඇත. උදාහරණයක් ලෙස යම් වැඩකදී යම් දිගක් මැනීමේදී මීටරය නම් ඒකකය විශාල වැඩි වීමට පුළුවන් (ඔබේ කොන්ඩය මීටර් අච්චරක් මෙච්චරක් දිග යැයි පවසන්නේ නැහැ නේද?) එවිට, ඊට වඩා කුඩා ඒකකයක් සමග වැඩ කිරීම පහසුවක් ගෙන දේ. මෙම ක්රමයේදී පහත දැක්වෙන සේ “ගුණක” (multipliers) හඳුන්වා දී තිබෙනවා. ඒ එක් එක් ගුණක පදයක් පෙර අප ඉගෙන ගත් ඒකකයක් ඉදිරියට දැමීමෙන් එම ගුණකයට අයිති අගයෙන් එක්කෝ එම ඒකකය කුඩා වෙනවා නැතිනම් විශාල වෙනවා. (සෙන්ටි, ඩෙසි හා ඩෙකා යන ඒවා හැර අනෙක් ගුණක එකින් එක වෙනස් වන්නේ යම් රටාවකට (දර්ශකය තුනෙන් තුනට) බව පැහැදිලියි නේද?) මෙම ගුණක පද යොදන විට, වචන අතර හැඩැසක් තබන්නේ නැත (උදා: kilogram මිසි kilo gram නොවේ).
femto (f) - 10-15 kilo (k) - 103
pico (p) – 10-12 mega (M) – 106
nano (n) – 10-9 giga (G) – 109
micro (µ) – 10-6 tera (T) - 1012
milli (m) – 10-3 peta (P) - 1015
centi (c) – 10-2 deca (da) – 102
deci (d) – 10-1 hecto (h) – 101 හෙවත් 10
pico (p) – 10-12 mega (M) – 106
nano (n) – 10-9 giga (G) – 109
micro (µ) – 10-6 tera (T) - 1012
milli (m) – 10-3 peta (P) - 1015
centi (c) – 10-2 deca (da) – 102
deci (d) – 10-1 hecto (h) – 101 හෙවත් 10
අප උදාහරණ කිහිපයක් සලකා බලමු. මීටරයට ඉදිරියන් කිලෝ යන ගුණකය දැමූ විට කිලෝමීටරය ලැබේ. එහි විශාලත්වය මීටරය මෙන් දහස් ගුණයකි. 1 kilometer (km) = 1000 meter (m). ග්රෑම් ඉදිරියෙන් මිලි යන ගුණකය දැමූ විට මිලිග්රෑම් ලැබේ. එහි විශාලත්වය ග්රෑමයෙන් දාහෙන් එක් ගුණයකි.
1milligram (mg) = 0.001 gram = 10-3 gram
1milligram (mg) = 0.001 gram = 10-3 gram
ඉහත දැක්වූයේ මූලික රාශි හා ඒවා මනින විවිධ ඒකක ගැනයි. මෙම රාශිවලින් වෙනත් රාශින් ව්යුත්පන්න (derive) කළ හැකියි. එලෙස ව්යුත්පන්න රාශින් සිය දහස් ගණනක් ඇති අතර, ඉන් කිහිපයක් පමණක් මා පහත දක්වනවා.
යම් ලක්ෂයක සිට වෙනස් දිශා දෙකකට දිගක් ගිය විට ඉන් ඇතිවන්නේ ක්ෂේත්රඵලය හෙවත් වර්ගඵලය (area), A යන ව්යුත්පන්න රාශියයි.
පැහැදිලිවම මෙම ක්ෂේත්රඵලය නම් රාශිය ඉහත කී දුර නමැති ඒකකය දෙදිශාවකට මැනීමෙන් ලැබුණු එකකි. (එම දිශා දෙක දිග හා පළල ලෙස හැඳින්විය හැකියි.) ක්ෂේත්රඵලය මැනීමේ සම්මත ක්රමය වන්නේ වර්ග මීටරය(square meter) (m2) වේ. ඊට හේතුව ඉහත රූපය බැලීමෙන් පැහැදිලි වේ. එනම්, මීටරය නම් ඒකකය එම ඒකකයෙන්ම වැඩි කළ විට වර්ග මීටරය ලෙස එය ලිවිය හැකියි.
තවද, සම්මත නොවන ඒකකද අපට ව්යුත්පන්න කළ හැකියි. උදාහරණයක් ලෙස, ඉහත රූපයේ පැති දෙක මැනීමට මීටරය වෙනුවට අඟල් යන ඒකකය භාවිතා කරන්නේ නම්, වර්ග අඟල් (square inch) (in2) යන ඒකකය ලැබේ. එලෙසම, වර්ග අඩි (square feet) (ft2), වර්ග මිලිමීටර් (mm2), ආදී ලෙස විවිධ ඒකකයන් පැවතිය හැකි බව පැහැදිලියි නේද? මෙවිතරක් නොව, ක්ෂේත්රඵලය මැනීමටම අලුතින් සාදාගෙන ඇති ඒකක කිහිපයක්ද ඇත. පර්චසය (perch), ආර (are), හෙක්ටෙයාරය (hectare) යනු එවැනි ඒකක කිහිපයකි.
1 perch = 272.25 ft2 (දිග හා පළල අඩි 16.5 බැගින් වූ සමචතුරස්රයක පවතින වර්ග අඩි ගණන මෙයයි.)
160 perches = 1 acre (අක්කර)
4 rd (rood - රූඩ්) = 1 අක්කර
1 are = 100 m2 (දිග හා පළල මීටර් 10 බැගින් වූ සමචතුරස්රයක පවතින වර්ග අඩි ගණන මෙයයි.)1 hectare = 100 ares
160 perches = 1 acre (අක්කර)
4 rd (rood - රූඩ්) = 1 අක්කර
1 are = 100 m2 (දිග හා පළල මීටර් 10 බැගින් වූ සමචතුරස්රයක පවතින වර්ග අඩි ගණන මෙයයි.)1 hectare = 100 ares
දිග පළලට අමතරව උසක්ද ඇති විටක එවැනි අවස්ථාවක පරිමාව (volume), V නම් ව්යුත්පන්න රාශිය ලැබේ.
එය ඝන මීටරය (cubic meter) (m3) නම් සම්මත ව්යුත්පන්න ඒකකයෙන් මැනේ. පෙර සේම, ඝන මයික්රොමීටර්, ඝන අඩි ආදී ඒකකයන්ද සාදාගත හැකියි. ක්ෂේත්රඵලයේදී මෙන්ම පරිමාව සඳහාද ඊටම සාදාගත් සම්මත නොවන ඒකක කිහිපයක් පවතී. බොහෝ විට ද්රව පරිමාවන් මැනීමට මෙම ඒකක භාවිතා කෙරේ.
3 tsp (tea spoon - තේ හැඳි) = 1 tbsp (table spoon - මේස හැඳි)
2 tbsp = 1 fl oz (fluid ounce - ද්රව අවුන්ස. මෙය ස්කන්ධය මැනීමට ගන්නා අවුන්ස (oz) වලින් වෙනස්ය.)16 tbsp = 1 c (cup - කෝප්ප)2 c = 1 pt (Pint - පයින්ට්)2 pt = 1 qt (quart - ක්වොර්ට්)2 qt = 1 gal (gallon - ගැලුම්)1 lt (liter - ලීටර්) = 1dm3 (ඝන ඩෙසිමීටර්) = 1000 cm3
4 dr (dram - ඩ්රෑම්. මෙය ස්කන්ධය කිරීමට භාවිතා කළ ඩ්රෑම් එකට වඩා වෙනස්ය.) = 1 tbsp
1 tsp = 5 ml (මිලිලීටර්) = (දළ වශයෙන්) 5 mg (මිලිග්රෑම්)
2 tbsp = 1 fl oz (fluid ounce - ද්රව අවුන්ස. මෙය ස්කන්ධය මැනීමට ගන්නා අවුන්ස (oz) වලින් වෙනස්ය.)16 tbsp = 1 c (cup - කෝප්ප)2 c = 1 pt (Pint - පයින්ට්)2 pt = 1 qt (quart - ක්වොර්ට්)2 qt = 1 gal (gallon - ගැලුම්)1 lt (liter - ලීටර්) = 1dm3 (ඝන ඩෙසිමීටර්) = 1000 cm3
4 dr (dram - ඩ්රෑම්. මෙය ස්කන්ධය කිරීමට භාවිතා කළ ඩ්රෑම් එකට වඩා වෙනස්ය.) = 1 tbsp
1 tsp = 5 ml (මිලිලීටර්) = (දළ වශයෙන්) 5 mg (මිලිග්රෑම්)
තවද, අක්කර-අඩි (එනම් යම් අක්කර ගණනක ක්ෂේත්රඵලයක් හා අඩි ගාණක ගැඹුරක් ලෙස පරිමාව සලකා බලන විට. මෙම ක්රමයෙන් ජලාශයක වැවක ජල පරිමාව සාමාන්යයෙන් මැනේ.), හෙක්ටයාර-අඩි ආදී ලෙසද ඔබට සුදුසු ඒකක කලවම් කරමින් විවිධ ව්යුත්පන්න ඒකක සෑදිය හැකිය. වාහනවල එන්ජින්වල ධාරිතාව (පරිමාව) පවසන්නේ CC (සීසී) යන වචනයෙනි. CC 1000, CC 850 ආදී ලෙස ඒවා ප්රකාශ කෙරෙනවා. මෙහි CC යනු cubic centimeter (ඝන සෙන්ටිමීටර්) වේ.
යම් දෙයක ස්කන්ධයක් එහි පරිමාවෙන් බෙදූ විට ලැබෙන්නේ එම ද්රව්යයේ ඝනත්වය (density), ρ වේ. ඒ අනුව, ඝනත්වයේ ඒකකය ලෙස “ඝන මීටරයට කිලෝග්රෑම්” වන අතර, එය ලියන්නේ kg/m3 ලෙසය. එහි ඇල ඉරට පසුව ඇති කොටස (එනම් භාගයේ හරය) උඩට (එනම් ලවයට) ගෙන ආ හැකියි සරල ගණිතය (දර්ශක නීතිය) උපයෝගි කරගෙන. එවිට එය, kgm-3 ලෙසද එයම ලිවිය හැකියි.
 = ඝනත්වය (ρ= M/V
= ඝනත්වය (ρ= M/V යම් (දෙයක් ගමන් කළ) දුරක් එම දුර යෑමට ගත වූ කාලයෙන් බෙදූ විට වේගය (speed)/ප්රවේගය (velocity), v ලැබේ. ප්රවේගය යනු යම් දිශාවකට එක එල්ලේ ගමන් කරන දුරකි (එමනිසා, එය එක ඍජු රේඛාවකින් නිරූපණය කළ හැකිය. මෙවැනි ඍජු දිගක් “දුර” (distance), s යන වචනයෙන් නොව “විස්ථාපනය” (displacement), d යන විශේෂ වචනයෙන් හැඳින් වේ. එමනිසා, ප්රවේගය යනු විස්ථාපනය කාලයෙන් බෙදූ විට ලැබෙන රාශිය ලෙසද අර්ථ දැක්විය හැකියි.) වේගය යනු එලෙස එක එල්ලේ නොව වංගු ගැසී පවතින ගමන් මාර්ගයක් ඔස්සේ ගමන් කරන විට, එම දුර ගෙවා යෑමට ගත වන කාලයෙන් බෙදූ විට ලැබෙන දෙයකි. මේ දෙකෙහිම සම්මත ඒකකය තත්පරයට මීටර් වේ. එය m/s ලෙස හෝ ms-1 ලෙස දැක්වේ.
වේගය = දුර / කාලය
පැයට කිලෝමීටර් (km/h or kmh-1 or kmph (kilometers per hour)) හා පැයට සැතපුම් (mi/h or mph (miles per hour)) ලෙසද වේගය/ප්රවේගය මැනිය හැකිය. වාහනවල වේගය බොහෝ විට කියන්නේ මෙවැනි ක්රමයකිනි.
විශ්වයේ තිබිය හැකි අවම උෂ්ණත්වය කෙල්වින් බිංදුවය. එමනිසා, එය විද්යාවේ නොවෙනස්වන වටිනා නියතයකි. එලෙසම විශ්වයේ එවැනි තවත් ඉතාම වැදගත් නියතයක් තමයි ආලෝකයේ වේගය (speed of light) කියා කියන්නේ. ආලෝකය (හෝ ඕනෑම විද්යුත් චුම්භක තරංගයක්) හිස් අවකාශය (හෙවත් රික්තයක්) තුළ ගමන් කරන වේගය මෙනමින් හැඳින් වේ. විශ්වයේ කිසිම පදාර්ථයකට හෝ ශක්තියකට මෙම වේගය ඉක්මවා යා නොහැකිය. එම වේගයේ අගය තත්පරයට කිලෝමීටර් ලක්ෂ තුනකි (300,000 kms-1). සැතපුම්වලින් ගත හොත් එය තත්පරයට සැතපුම් 186,000 කි. මෙම නියතය c යන සංඛේතයෙන් දැක්වේ.
ප්රවේගය නැවත කාලයෙන් බෙදූ විට ත්වරණය (acceleration), a යන ව්යුත්පන්න රාශිය ලැබේ. ත්වරණය යනු කාලයත් සමග යම් ප්රවේගයක් අඩු හෝ වැඩි වීමයි (කාලයත් සමග ප්රවේගය අඩුවන විට එය ඍණ ත්වරණයක් ලෙස සැලකේ.) වාහනයක් නිශ්චලව සිට ගමන් ආරම්භ කර ක්රමයෙන් වේගය වැඩි කරගන්නවා නේද? එලෙසමයි, ගමන් කරන වාහනයක් නැවැත්වීමට ක්රමයෙන් වේගය අඩු කරමින් එය නිශ්චල කරනවා. මෙන්න මෙවැනි වේගය වැඩි වීමක් (හෝ අඩු වීමක්) තමයි ත්වරණය කියන්නේ. මේ අනුව මෙහි ඒකකය ඔබට සිතා ගත හැකියි නේද? එනම්, (m/s) නැවත s වලින් බෙදිය යුතුය; (m/s)/s = m/(S x S) = m/s2 වේ. මෙය ms-2 ලෙසද ලිවිය හැකි බව ඔබට දැන් පේනවා. “තත්පර වර්ගයට මීටර්” (meters per square second) ලෙස මෙය ශබ්ද කෙරෙනවා.
යම් ඒකාකාර ප්රවේගයකින් ගමන් කරන දෙයක ස්කන්ධය එහි ප්රවේගයෙන් වැඩි කළ විට ගම්යතාව (momentum), m ලැබේ. ඒ අනුව එහි ඒකකය kgms-1 වේ.
ගම්යතාව = ස්කන්ධය x ප්රවේගය (kg x ms-1)
යම් ත්වරණයකින් ගමන් කරන දෙයක ස්කන්ධය එහි ත්වරණයෙන් වැඩි කළ විට ලැබෙන්නේ බලය (force) වේ. එහි ඒකකය kgms-2 වේ. එහෙත් මෙම ඒකකය තරමක් දිග වැඩි නිසාත්, මෙම රාශිය නිතර නිතර පාවිච්චි කෙරෙන නිසාත්, ඊට වෙනත් කෙටි ඒකකයක් ඒ වෙනුවට හඳුන්වාදී ඇත. එම අලුත් ඒකකය නිව්ටන් (Newton) (N) වේ. විද්යාව තුළ මේ ආකාරයට දිගු ඒකකවලට කෙටි නම් හඳුන්වාදීම සුලභ සිද්ධියකි.
1 N = 1 kgms-2 (මින් පෙනී යන්නේ ඒකක දෙකහිම අගය එකම වන බවයි. නම පමණක් අලුත් හා කෙටි වී ඇත.)
පදාර්ථ හා ශක්තිය ගැන කතා කරන විටත් අප බලය ගැන ඉහතකදී කතා කළා මතකද? බලය යනු යම් ශක්තියක් පිටුපස තිබෙන එම ශක්තියට යම් යම් දේවල් කිරීමට හැකියාව ලබා දෙන ගුණයකි. විවිධ ශක්තින් විවිධ අයුරින් ක්රියාත්මක වන නිසා බලයද ඊට අනුරූපව ක්රියාත්මක වෙනවා. උදාහරණයක් ලෙස ආලෝකය ශක්තියකි. එය අපිට (අපේ ඇස්වලට) පේනවා. තාපය යනුද තවත් ශක්තියකි. එය අපිට පෙනෙන්නේ නැති වුවත් ඇඟට දැනෙනවා. මේ දෙකම එකිනෙකට වෙනස් ආකාරයේ ශක්ති දෙකකි. එහෙත් අවසාන වශයෙන් මෙම ශක්තීන් දෙකම මනින්නේ (ජූල් ලෙස හැඳින්වෙන) එකම ඒකකයෙනි. ඊට හේතුව, පවතින ආකාරය කුමක් වුවත් සෑම ශක්ති විශේෂයක්ම එකිනෙකාට පොදු බවයි. එලෙසම සෑම බලයකම අවසාන වශයෙන් භෞතික වශයෙන් යම් පොදු බවක් තිබෙනවා. එමනිසා, යම් ශක්තියක් තවත් ඊට වඩා වෙනස් ආකාරයේ ශක්තියක් සමග සංසන්දනය කළ හැකි සේම, යම් බලයක් තවත් ඊට වඩා වෙනස් බලයක් සමග සංසන්දනය කළ හැකිය. මෙය උපමාවකින් තවදුරටත් පෙන්වා දෙන්නම්. ඔබේ “ඇඟ බස්ස ගන්න” ඔබට දිවිය හැකිය. පිහිනිය හැකිය. සෙල්ලම් කළ හැකිය. මේ සියල්ලම එකිනෙකට වෙනස් ආකාරයේ ක්රියාකාරකම් වුවද, මේ සියල්ලන්ගේම අවසන් ප්රතිපලය ඔබේ ඇඟ කෙට්ටුකර ගැනීම නේද? මෙම විවිධ ක්රියාකාරකම් ඔබට සංසන්දනය කළ හැකිය (විනාඩි විස්සක් දුවන එක විනාඩි දහක පිහිනීමකට සමානයි ආදී වශයෙන්). විවිධ ශක්ති හා විවිධ බලයන් ගැනද සිතිය යුත්තේ එලෙසයි.
සමහර බලයන් (හා ශක්තින්) ඍජුවම මැනීම පහසු නැති අතර සමහර බල පහසුවෙන් ඍජුවම මැනිය හැකිය. යම් වස්තුවක චලනය ඉතා පහසුවෙනුත් නිවැරදිවත් ඍජුවම මැනිය හැකියි. වස්තුවක් චලනය වන්නට ශක්තියක් භාහිරින් යෙදිය යුතුය. එනම්, බලයක් භාහිරින් යෙදිය යුතුය. අයිසැක් නිව්ටන් නම් මහා විද්යාඥයා මෙම බලයක් යෙදීමෙන් වස්තු චලනය වීම පිළිබඳ පර්යේෂණ සිදු කර ඉතා වැදගත් සේම ඉතා සරල රීති කිහිපයක් හඳුන්වා දුන්නේය. ඒවා අද නිව්ටන්ගේ නීයම (Newton’s Laws) හෝ චලනය පිළිබඳ නිව්ටන්ගේ නියම ලෙස පාසල්වල පවා ඉගැන්වේ. නිව්ටන්ගේ නියම තුනක් පවතී.
නිව්ටන්ගේ නියම
1. යම් වස්තුවක් නිශ්චලව ඇති විටකදී එම වස්තුව චලනය කිරීමට හෝ යම් වස්තුවක් ඒකාකාර ප්රවේගයකින් එක කෙළින් (වංගු නැතිව) ගමන් කරන විටකදී, එම වස්තුවේ ප්රවේගය වෙනස් කිරීමට හෝ ගමන් කරන මාර්ගය වෙන අතකට හැරවීමට නම්, අනිවාර්යෙන්ම පිටතින් එම වස්තුවට යම් බලයක් ලබා දිය යුතුමය. (නිව්ටන්ගේ පළමු නියමය)
2. ඉහත ආකාරයට භාහිරින් යම් බලයක් ලබා දුන් විට, එම වස්තුව ත්වරණයකට ලක්වන අතර, එම ත්වරණය පිටතින් ලබා දුන් බලයට සමානුපාතික වේ. මෙය කෙටියෙන් සූත්රයක් ආකාරයට පහත ආකාරයට ලිවිය හැකිය. (නිව්ටන්ගේ දෙවන නියමය)
බලය = (වස්තුවේ ස්කන්ධය) x (වස්තුවේ ත්වරණය)
(Force = mass x acceleration)
F = ma ලෙස මෙය කෙටි සංඛේත ක්රමයෙන් දැක්වේ.
මෙම සූත්රය අනුව බලය යන රාශිය පහසුවෙන් මැනගත හැකි ක්රමයක් අපට දැන් තිබෙන බව පේනවා.
බලය = (වස්තුවේ ස්කන්ධය) x (වස්තුවේ ත්වරණය)
(Force = mass x acceleration)
F = ma ලෙස මෙය කෙටි සංඛේත ක්රමයෙන් දැක්වේ.
මෙම සූත්රය අනුව බලය යන රාශිය පහසුවෙන් මැනගත හැකි ක්රමයක් අපට දැන් තිබෙන බව පේනවා.
3. යම් කිසි වස්තුවකට බලයක් පිටතින් ලබා දුන් විට, එම වස්තුව විසින්ද ඒ පිටතින් ලබා දුන් බලයට සමාන එහෙත් ඊට ප්රතිවිරුද්ධ දිශාවට යොමු වූ ප්රතිබලයක් හෙවත් ප්රතික්රියා බලයක් ඇති කරනවා. මෙය බොහෝ දෙනා කියන්නේ “සෑම ක්රියාවකට සමාන වූත් ප්රතිවිරුද්ධ වූත් ප්රතික්රියාවක් ඇත” යනුවෙනි. (නිව්ටන්ගේ තෙවැනි නියමය)
ඔබ අත මිට මොලවා වැරෙන් බිත්තයට පහරක් දුන් විට, සත්ය වශයෙන්ම ඔබ සිදු කළේ යම් කිසි බලයක් බිත්තියට යොමු කිරීමයි. එහිදී නිව්ටන්ගේ තෙවන නියමය අනුව ඒ ක්ෂණයෙන්ම ඔබ බිත්තිය දෙසට යොමු කළ බලයට සමාන බලයක් බිත්තිය විසින් ඔබේ අත දෙසට ලබා දේ. ඔබ බිත්තයට ගැසූ විට ඔබේ අත රිදෙන්නේ ඇත්තටම මෙන්න මෙම ප්රතික්රියා බලය නිසාය. අහස් කූරක් හෝ රොකට් ගමන් කරන්නේද මෙම තෙවැනි නියමයේ මහිමයෙනි. එනම් අහසු කූරේ (හෝ රොකට් එකේ) කෙළවරින් වෙඩි බෙහෙත් දල්වා එම ගින්දර කූරේ පිටුපසින් වේගයෙන් පහළට යොමු කෙරේ. එවිට, එම කූරේ කෙළවරට තෙවන නියමය අනුව ප්රතික්රියා බලයක් ලැබීමෙන් එම කූර ඉහළට ගමන් කරයි. පුම්බපු බැලුමක කට ගැට නොගසා අත හැරිය විට බැලුම වේගයෙන් උඩ යන්නේද මෙම තෙවන නියමය නිසාය.
ඔබ අත මිට මොලවා වැරෙන් බිත්තයට පහරක් දුන් විට, සත්ය වශයෙන්ම ඔබ සිදු කළේ යම් කිසි බලයක් බිත්තියට යොමු කිරීමයි. එහිදී නිව්ටන්ගේ තෙවන නියමය අනුව ඒ ක්ෂණයෙන්ම ඔබ බිත්තිය දෙසට යොමු කළ බලයට සමාන බලයක් බිත්තිය විසින් ඔබේ අත දෙසට ලබා දේ. ඔබ බිත්තයට ගැසූ විට ඔබේ අත රිදෙන්නේ ඇත්තටම මෙන්න මෙම ප්රතික්රියා බලය නිසාය. අහස් කූරක් හෝ රොකට් ගමන් කරන්නේද මෙම තෙවැනි නියමයේ මහිමයෙනි. එනම් අහසු කූරේ (හෝ රොකට් එකේ) කෙළවරින් වෙඩි බෙහෙත් දල්වා එම ගින්දර කූරේ පිටුපසින් වේගයෙන් පහළට යොමු කෙරේ. එවිට, එම කූරේ කෙළවරට තෙවන නියමය අනුව ප්රතික්රියා බලයක් ලැබීමෙන් එම කූර ඉහළට ගමන් කරයි. පුම්බපු බැලුමක කට ගැට නොගසා අත හැරිය විට බැලුම වේගයෙන් උඩ යන්නේද මෙම තෙවන නියමය නිසාය.
යම් බලයක් යම් මතුපිටක් හෙවත් ක්ෂේත්රඵලයක් මත යොදන විට, අප ඊට පීඩනය (pressure), p කියා පවසනවා.
මෙය මනින සම්මත ඒකකය “වර්ග මීටරයට නිව්ටන්” (N/m2 or Nm-2) වේ. මීටම පැස්කල් (Pascal) (Pa) යන සම්මත ඒකකය හඳුන්වාදී තිබෙනවා. තවත් ඒකක ගණනාවක් තිබෙනවා පීඩනය මැනීම සඳහාම.
1 atm (atmospheric pressure - වායුගෝල පීඩන) = 100,000 Pa (=100 kPa)
1 bar = 1 atm = 100 kPa1 PSI (Pounds per Square Inch - වර්ග අඟලකට රාත්තල්) = 6.9 kPa
1 Hgmm (Mercury millimeter - රසදිය මිලිමීටර්) = 133 Pa
1 torr (ටෝර්) = 1 Hgmm
1 bar = 1 atm = 100 kPa1 PSI (Pounds per Square Inch - වර්ග අඟලකට රාත්තල්) = 6.9 kPa
1 Hgmm (Mercury millimeter - රසදිය මිලිමීටර්) = 133 Pa
1 torr (ටෝර්) = 1 Hgmm
පොලොවේ මතුපිට (මුහුදු මට්ටම) සිට කිලෝමීටර් ගණනාවක් ඉහළට වායුගෝලය (atmosphere) පිහිටා තිබේ. මෙම වායු තට්ටුවෙන් යම් පීඩනයක් ඊට යටින් තිබෙන සියලු දේවලට ඇති වේ. මෙම පීඩනය “වායුගෝල පීඩන එකක්” හෙවත් “1 atm” ලෙස අර්ථ දක්වා ඇත. මෙය ලෝකයේ තැනින් තැනට ස්වල්ප ලෙස වෙනස් වන අතර, මුහුදු මට්ටමේ සිට ඉහළට යන විට එම පීඩනය අඩු වන බවද ඔබට සිතා ගත හැකියි.
ජලයේ (ගඟක හෝ මුහුදේ) යටට යන්නට යන්නට පීඩනයද ක්රමයෙන් වැඩි වේ. දළ වශයෙන් ජලය යටට යන සෑම 10 m ක් පාසාම 1 atm හෙවත් 1 bar බැගින් වැඩි වේ. උදාහරණයක් ලෙස, ඔබ අඩි 20 ක් යටින් මුහුදේ පිහිනනවා නම්, ඔබේ ශරීරය මත 3 bar පීඩනයක් (සාමාන්ය වායුගෝල පීඩනය හා ජලයේ අඩි 20 නිසා ඇති වූ තවත් වායුගෝල පීඩන දෙකක්) පවතී.
යමක් උල් (pointed) හෝ යමක් කැපෙන මුවහත් (sharp) යනුවෙන් සඳහන් කරන විටද, අප ඒ කතා කර තිබෙන්නේ පීඩනය ගැන තමයි. පිහි තලයක් මුවහත් යනු, එම දාරයේ ක්ෂේත්රඵලය ඉතා අඩු බවයි. අප තලයක් මුවහත් කරන විට කරන්නේ එම දාරය තවත් තුනී වන තෙක් ඇතිල්ලීමයි (හෙවත් එම දාරයේ ක්ෂේත්රඵලය අඩු කිරීමයි). එවිට, ඔබ එම මුවහත් තලය පාන් හෝ බටර් හෝ වෙනත් ඕනෑම දෙයක් මත තබා අතින් බලය දුන් විට, ඉහත පීඩනයේ සූත්රය අනුව ඔබ ලබා දෙන බලය පිහි තලයේ ඉතා කුඩා ක්ෂේත්රඵලයෙන් බෙදූ විට ඉතා අධික පීඩනයක් එම පාන් හෝ බටර් හෝ වෙත ලැබී එය පහසුවෙන් කැපේ.
ඝන, ද්රව, වායු යන පදාර්ථයේ අවස්ථා තුනෙන් ද්රව හා වායු යන දෙයාකාරයෙන් පවතින ද්රව්ය පීඩනය, උෂ්ණත්වය යන දෙක හමුවේ බොහෝ විට හැසිරෙන්නේ එකම ආකාරයෙනි. එමනිසා, ද්රව හා වායු යන දෙකට තරල(fluid) යන තනි වචනයද භාවිතා කරනවා. යම් තරලයක උෂ්ණත්වය වැඩි කරගෙන යන විට, වේගයෙන් එම තරලය ප්රසාරණය (expand) වෙනවා. යම් වායුවක් මත පීඩනයක් එල්ල කළ විට, එම වායුව සංකෝචනය(compress) වෙනවා. එහෙත් බොහෝ ද්රව මතට පීඩනයක් එල්ල කළ විට, එම ද්රවය සංකෝචනයක් සිදු නොවන තරම්ය (එනම්, බොහෝ ද්රව සංකෝචනය කළ නොහැකි හෙවත් incompressible වේ.) වායුවක් වුවද, පීඩනය ක්රමයෙන් වැඩි කරගෙන යාමේදී තව දුරටත් සංකෝචනය නොවිය හැකි මට්ටමකට පැමිණෙනවා.
යම් සංවෘත බහලුමක ඇති යම් ඉන්කොම්ප්රෙසිබල් (එනම්, තවදුරටත් සංකෝචනය කළ නොහැකි) තරලයකට පීඩනයක් ලබා දුන් විට එම පීඩනය එම තරලයේ සෑම තැනකින්ම එම බහලුමේ බිත්ති මත එල්ල වේ. මෙයපැස්කල් නියමය (Pascal’s law) ලෙස හැඳින්වේ.
මෙම පැස්කල් නියමය කර්මාන්වල නැතිවම බැරි තරමට ප්රයෝජනවත්ය. වාහන හෝ ඕනෑම බර අධික දේවල් එසවීමට භාවිතා කරන ජැක්, කෝච්චි හා වාහනවල භාවිතා කරන හයිඩ්රෝලික් බ්රේක්ද වැඩ කරන්නේ මෙම සිද්ධාන්තය මතය. පැස්කල් නියමය ද්රව තරල උපයෝගි කරගන්නා විටදී එවැනි භාවිතාවන්/ඇටවුම් hydraulic (හයිඩ්රෝලික්) ලෙසද, වාතය යොදාගන්නා විට pneumatic (නියුමැටික්) ලෙසද හැඳින්වෙනවා.
යම් බලයක් වස්තුවකට යෙදීමෙන් එම වස්තුව චලනය වේ නම්, එම බලය වස්තුව ගමන් කළ දුරින් වැඩි කළ විට අපට ලැබෙන්නේ “කාර්යය” (work), w නම් රාශියයි.
කාර්යය (හෙවත් ශක්තිය) = බලය x (ගමන් කළ දුර) (w=Fd)
මෙහි ඒකකය ඒ අනුව නිව්ටන් මීටර් (Nm) වේ. මීටම ජූල් (Joule) (J) යන ඒකක නාමය (හා සංඛේතය) හඳුන්වා දී ඇත. කාර්යයක් කළා යනු යම් ශක්තියක් වැය කළා යන බවයි ඉන් හැඟවෙන්නේ. ඒ අනුව ශක්තිය යනු කාර්යයම වේ. ඒ අනුව, ශක්තියේ ඒකකයද Nm හෝ J වේ. (ශක්තිය හා බලය අතර ඇති ඉතා සරල හා වැදගත් සම්බන්ධතාව ඉහත සූත්රයෙන් දැන් ඔබට මතක තබා ගත හැකියි.)
ඉහත (නිව්ටන් මීටර් හෝ) ජූල් යන සම්මත ඒකකයට අමතරව, කැලරි, බීටීයූ ආදී තවත් ඒකකද ශක්තිය මැනීමට භාවිතා වෙනවා.
4.2 J = 1 c (calorie) (ආහාරවල ඇති ශක්තින් සාමාන්යයෙන් මෙම ඒකකයෙන් මැනේ.)
1055 J = 1 BTU (British Thermal Unit. ෆ්රිජ් ඒසී වැනි උපකරණවල ශක්තිය සාමාන්යයෙන් මනින්නේ මෙම ඒකකයෙනි.)
1 eV (electron volt) = 1.60x10-19 J (පරමාණු හා අණු අතර සිදුවන ශක්තින් මෙම කුඩා ඒකකයෙන් මැනේ.)
1 Wh (Watt-hour) = 3600 J (= 3.6 kJ) (ඇත්තටම වොට් අවර් එකක් යනු තත්පරයකට වොට් 1 බැගින් පැයක් හෙවත් තත්පර 3600ක් ඇතුලත වැය කරන ශක්තිය වේ.)
1055 J = 1 BTU (British Thermal Unit. ෆ්රිජ් ඒසී වැනි උපකරණවල ශක්තිය සාමාන්යයෙන් මනින්නේ මෙම ඒකකයෙනි.)
1 eV (electron volt) = 1.60x10-19 J (පරමාණු හා අණු අතර සිදුවන ශක්තින් මෙම කුඩා ඒකකයෙන් මැනේ.)
1 Wh (Watt-hour) = 3600 J (= 3.6 kJ) (ඇත්තටම වොට් අවර් එකක් යනු තත්පරයකට වොට් 1 බැගින් පැයක් හෙවත් තත්පර 3600ක් ඇතුලත වැය කරන ශක්තිය වේ.)
සටහන
එස්අයි ඒකකවලට පමණක් නොවේ මිලි, මෙගා ආදී ලෙස ඉහතදී පෙන්වා දුන් ගුණක පද යෙදිය හැක්කේ. අවශ්ය නම් වෙනත් ඒකකයන් සමගද ඒවා යෙදිය හැකිය. උදාහරණ ලෙස,
එස්අයි ඒකකවලට පමණක් නොවේ මිලි, මෙගා ආදී ලෙස ඉහතදී පෙන්වා දුන් ගුණක පද යෙදිය හැක්කේ. අවශ්ය නම් වෙනත් ඒකකයන් සමගද ඒවා යෙදිය හැකිය. උදාහරණ ලෙස,
milliliter - ml (0.001 liter), kilocalorie - kc (1000 calories), Mega electron volt – MeV (1,000,000 eV)
යම් ශක්තියක් කාලයෙන් බෙදූ විට, එය ක්ෂමතාව හෙවත් ජවය (power), P ලෙස හැඳින්වේ. ජවය යනු සෑම තත්පරයකදීම යම් උපකරණයක් හෝ දෙයක් වැය කරන (හෝ ලබා ගන්නා) ශක්තිය ලෙස සැලකීමට පුරුදු වන්න. මෙය තත්පරයට ජූල් (J/s or Js-1) යන ඒකකයෙන් මැනේ. මීටම වොට් (Watt) (W) යන ඒකක නාමය හඳුන්වාදී ඇත.
ජවය = ශක්තිය / කාලය
අශ්වබලය (horsepower - hp) යන ඒකකයක්ද ජවය මැනීමට ඇත. ආදි කාලයේ කරත්ත ආදිය පැදවීමට යෙදෙව්වේ අශ්වයන්ය (ලංකාව වගේ රටවල අශ්වයන් වෙනුවට හරක් යොදාගන්නවා.) එහිදී දළ වශයෙන් එක් අශ්වයෙක් සතු ජවය අශ්වබල එකක් ලෙස හැඳින් වේ. යම් කරත්තයකට අශ්වයන් දෙන්නෙක් යෙදෙව්වොත් එතැන අශ්වබල දෙකක ජවයක් තිබේ. පසු කාලීනව අශ්වයන් නොයොදා ඇති විටත්, අශ්වබල නම් ඒකකය මෝටර් වැනි උපකරණ ආදියේ ජවය දැක්වීමට භාවිතා කෙරේ.
1 hp = 746 W
යම් බලයක් යෙදූ විට වස්තුවක චලිතයේ (motion) යම් යම් වෙනස්කම් ඇතිවන බව නිව්ටන් නියම අනුව ඔබට පෙනෙනවා. මෙලෙස සිදු විය හැකි චලිත ප්රධාන වශයෙන් දෙයාකාරය. එකක් නම්, රේඛීය චලිත (linear motionහෝ translational motion) වේ.
මෙහිදී බලය යොදා ඇති දිශාවට රේඛාවක් ඔස්සේ ගමන් කරන්නාක් සේ මෙම චලිතය සිදු වේ. තවත් වර්ගයේ චලිතයක් නම් වෘත්ත චලිත (circular motion) වේ. මෙහිදී වස්තුව ගමන් කරන්නේ “වටේට” (“රවුමට”) වේ. මෙය රේඛිය නොවන (non-linear) චලිතයකි.
ඉහතදී සඳහන් කළ ප්රවේගය, ත්වරණය, ගම්යතාව ආදී රාශින් ඇත්තටම අදාල වන්නේ රේඛිය චලිත සඳහා පමණි. වෘත්ත චලිතවලදීද ඒ රාශි වෙනුවට පවතින්නේ වෙනත් රාශින්ය. එනම්, වෘත්ත චලිතයට ගැලපෙන ලෙස එම රාශින් යම් යම් වෙනස් ආකාරවලින් අර්ථ දක්වා ඇත. ඒවා එකින් එක දැන් සලකා බලමු.
රේඛිය චලිතයකදී යම් සරල රේඛාවක් අනන්තය දක්වා විහිදිය හැකිය. එනම් විස්ථාපනය අනන්තය දක්වා විහිදිය හැකිය. එහෙත් වෘත්ත චලිතයක යෙදෙන වස්තුවක් එසේ නොවේ. එවැනි වස්තුවක් යම් ලක්ෂයක් වටා වෘත්තාකාරව ගමන් කරන විට එය අංශක 360 ක් (හෙවත් රේඩියන් 2π) ගමන් කර නැවතත් හිටපු තැනටම පැමිණෙනවා. එනම්, වස්තුව ගමන් කරන්නේ එකම වටයකය.
එනිසා, වෘත්ත චලිතයකදී අපට වඩා වැදගත් වන්නේ එම වෘත්ත චලිතයේ යෙදෙන වස්තුව ගමන් කරන අංශක ප්රමාණය මිස දුර නොවේ. රේඛීය චලිතයේ දුරට තිබෙන ස්ථානය වෘත්ත චලිතවලදී හිමි කර ගන්නේ කෝණය හෙවත් අංශක ගණන විසින්ය. ඒ අනුව සිතුවොත් ඔබට පහසුවෙන් වෘත්ත චලිත සඳහා රාශින් පහත ආකාරයට අර්ථ දැක්විය හැකියි.
යම් වස්තුවක් ගමන් කරන කෝණය කෝණික විස්ථාපනය (angular displacement), θ ලෙස හැඳින් වේ. එය කෝණයක් නිසා එහි සම්මත ඒකකය රේඩියන් වේ. අවශ්ය නම් අංශකය යන සම්මත නොවන කෝණයෙනුත් මැනිය හැකි බව දැන් ඔබට තේරෙනු ඇත.
කෝණික ප්රවේගය (angular velocity), ω යනු යම් වස්තුවක් ගමන් කළ කෝණය (හෙවත් කෝණික විස්ථාපනය) එම කෝණික විස්ථාපනය ගමන් කිරීමට ගත වූ කාලයෙන් බෙදූ විට ලැබේ. ඒ අනුව මෙහි සම්මත ඒකකය “තත්පරයට රේඩියන්” (rad/s හෝ rads-1) වේ.
කෝණික ප්රවේගය = කෝණික විස්ථාපනය / කාලය (ω= θ/t
එලෙසම කෝණික ත්වරණය (angular acceleration), α යන්නද පහසුවෙන් අර්ථ දැක්වීමට දැන් ඔබට පුලුවන් විය යුතුයි. එහි සම්මත ඒකකය rads-2 වේ. කෝණික ත්වරණය යනු වස්තුව වෘත්තාකාරව චලනය වන විට එම වස්තුව ක්රම ක්රමයෙන් කෝණික ප්රවේගය වැඩි (හෝ අඩු) කර ගැනීමයි.
කෝණික ත්වරණය = කෝණික ප්රවේගය / කාලය
යම් දෙයක් තත්පරයකට කැරකෙන වට ගණන එහි සංඛ්යාතය (frequency), f ලෙස හැඳින් වේ. එය මනින සම්මත ඒකකය හර්ට් (Hertz) (Hz) වේ. තත්පරයකට වට දහයක් කැරකැවේ නම්, එහි සංඛ්යාතය හර්ට්ස් දහයකි (10 Hz). යමක් තත්පරයකට වට භාගයක් කැරකැවේ නම්, එහි සංඛ්යාතය 0.5 Hz වේ. තවද, තත්පරයකට නොව විනාඩියකට කරකැවෙන වට ගණනද (revolutions per minute - RPM) නිතර භාවිතා වන රාශියකි. RPM යනුවෙන් බොහෝ අවස්ථාවල කියන්නේ මෙයයි (ආර්පීඑම් අගය 60න් බෙදීමෙන් අපට හර්ට්ස් වලින් මනින සංඛ්යාතය පහසුවෙන්ම ලැබේ.)
යමක් සම්පූර්ණ එක් වටයක් කැරකැවීමට ගතවන කාලය ආවර්ථය (period), T ලෙස හැඳින් වේ. සංඛ්යාතය හා ආවර්ථය අතර ඇත්තේ සරල සම්බන්ධතාවකි. සංඛ්යාතය (f), කෝණික ප්රවේගය (ω), ආවර්ථය (T) යන ඒකක තුන අතර පහත ආකාරයේ සම්බන්ධතා ගොඩනැගිය හැකියි.
යම් ස්කන්ධයක් මත කෝණික ත්වරණයක් යෙදූ විට (එනම්, යම් වස්තුවක් කෝණික ත්වරණයක් සහිතව වෘත්ත මාර්ගයක ගමන් කරන විට), ඊට කෝණික බලය (angular force) යන වචනයෙන් හැඳින්විය හැකි රාශියක් ලැබේ.
කෝණික බලය = ස්කන්ධය x (කෝණික ත්වරණය)
ඇත්තටම කෝණික බලය එතරම් ප්රචලිත හෝ භාවිතාවන එකක් නොවේ. ඒ වෙනුවට අප භාවිතා කරන්නේ ව්යාවර්ථය (Torque), τ යන රාශියයි. ඊට හේතුව මා කෙටියෙන් පෙන්වන්නම්. පහත රූපය බලන්න. දොර සරනේරුවලින් සවි වී ඇති නිසා, එය අරින වසන විට සරනේරු වටා ඇතිවන්නේ වෘත්ත චලිතයක් බව පෙනේ.
මෙහි A නම් ස්ථානයට ඇඟිල්ල තබා දොර වසන්නට උත්සහ කරනවා යැයි සිතන්න. එලෙසම B හා C යන ස්ථානවලටද එම ඇඟිල්ලම තබා දොර වසන්නට උත්සහ කරමු. මෙය ප්රායෝගිකවම ඔබට ඔබේ නිවසේ දොරකට කර බැලිය හැකියි. මෙහිදී A ස්ථානයට වඩා B ස්ථානයටද, B ස්ථානයට වඩා C ස්ථානයටද ඇඟිල්ල තබා එය වසන විට පහසුවක් දැනේ. එනම්, යම් වස්තුවක් මත වෘත්ත චලිතයක් ඇති වන ආකාරයට බලය යොදන විට, එම බලය යොදන ස්ථානය කේන්ද්රයේ සිට ඈත්වන්නට වන්නට එම වස්තුව පහසුවෙන් චලනය කරවිය හැකිය. (පහත රූපයෙන් එය පැහැදිලි වෙනවා. කේන්ද්රයේ සිට r ලම්භ දුරකින් පිහිටි ලක්ෂ්යකට F නම් බලයක් ලබා දීමෙන් ඇතිවන කැරකැවීමම ලබා ගැනීමට r/2 ක ලම්භක දුරකින් පිහිටි ලක්ෂ්යකට දිය යුත්තේ 2F බලයකි. ඒ ආදී ලෙස අනෙක් ලක්ෂ්ය ගැනද සිතන්න.)
සටහන
ඕනෑම වෘත්ත චලිතයක යෙදිය හැකි දේකට (ඉහත දොර මෙවැන්නකි; ඊට බලයක් යෙදූ විට එය කැරකේ.) කේන්ද්රයේ සිට d ලෙස හැඳින්වෙන යම් දුරකට ලම්භකව F ලෙස හැඳින්වෙන බලයක් ලබා දුන් විට, එයට බල ඝූර්ණය (moment) කියා කියනවා. මතක තබා ගන්න මෙහි අනිවාර්යෙන්ම බලය හා දුර ලබ්භක විය යුතුයි.
ඕනෑම වෘත්ත චලිතයක යෙදිය හැකි දේකට (ඉහත දොර මෙවැන්නකි; ඊට බලයක් යෙදූ විට එය කැරකේ.) කේන්ද්රයේ සිට d ලෙස හැඳින්වෙන යම් දුරකට ලම්භකව F ලෙස හැඳින්වෙන බලයක් ලබා දුන් විට, එයට බල ඝූර්ණය (moment) කියා කියනවා. මතක තබා ගන්න මෙහි අනිවාර්යෙන්ම බලය හා දුර ලබ්භක විය යුතුයි.
ඝූර්ණය = (කේන්ද්රයේ සිට දුර) x (ඊට ලම්භකව ලබා දෙන බලය) moment = F x d
ඝූර්ණය වැඩි වන විට, කරකැවීමත් පහසු වෙනවා. බලය වැඩි වීමෙනුත් කේන්ද්රයේ සිට බලය යොදන තැනට ඇති දුර ප්රමාණය වැඩි වීමෙනුත් ඝූර්ණය වැඩි වෙනවා.
ඕනෑම වස්තුවක් සෑදී ඇත්තේ කුඩා අංශුවලිනි. එම වස්තුව කුමන හෝ ආකාරයකින් චලනය වෙනවා යනු එම අංශු චලනය වීමයි. රේඛීය චලිතයකදී එය එතරම් ගණන් නොගත්තත්, වෘත්ත චලිතවලදී මෙය සැලකිල්ලට ගත යුතු වෙනවා. යම් වස්තුවක් වෘත්ත චලිතයක යෙදෙන විට, එම වස්තුව සැදුම් ලත් කුඩා අංශුවලට කැරකීමට ඇති හැකියාව එම අංශුව පිහිටා තිබෙන තැන අනුව වෙනස් වෙනවා (මෙය හරියට අර දොර වහන එක ඇඟිල්ල තබන ස්ථානය අනුව පහසු අපහසු වෙනවා බදුය). එනම්, එක් එක් කුඩා අංශුව සැලකුවොත් ඒවායේ එකිනෙකට වෙනස් ඝූර්ණයන් පවතිනවා.
එහිදී වස්තුවේ යම් අංශු (කේන්ද්රයේ සිට ඈතින් පිහිටි අංශු) පහසුවෙන් කැරකීමට උත්සහ දරන අතර තවත් අංශු (කේන්ද්රයට ළඟින් පිහිටි අංශු) කැරකැවීමට අපහසුවක් (මැලිකමක්) දක්වනවා. (මෙම ස්වභාවය ඇත්තටම කර්මාන්තවල ප්රායෝගිකව විවිධ දේවල් සිදු කිරීමට යොදා ගත හැකියි.) මෙම ස්වභාවය නිසා වස්තුවේ ස්කන්ධය පමණක් නොසලකා ඒ වෙනුවට ආවස්ථික ඝූර්ණය (moment of inertia), I යන රාශිය භාවිතයට ගන්නවා. එක් අංශුවක් සඳහා ආවස්ථික ඝූර්ණය ගණනය කිරීම ඉතාම පහසුවෙන් mr2 යන සූත්රයෙන් කළ හැකියි (මෙහි m යනු අංශුවේ ස්කන්ධය වන අතර r යනු එම අංශුව වෘත්ත චලිතයේ යෙදෙන කේන්ද්රයේ සිට ඇති දුර ප්රමාණයයි). එහෙත් අපට (ඇසටවත් නොපෙනෙන තරම්) අංශුවක චලිතය වැදගත් නැත. අපට වැදගත් වන්නේ අංශු කෝටි ප්රකෝටි ගණනක් එකතු වී සෑදෙන වස්තූන්ය. එහෙත් එවැනි වස්තූන්හි ආවස්ථික ඝූර්ණය වස්තුවේ හැඩය (එනම් එම වස්තුවේ අංශු පිහිටා ඇති ආකාරය) මත රඳා පවතිනවා.
එය සරල සූත්රයකින් ගණනය කළ හැකියි. එය ගණනය කිරීම සරල වුවත් එය කිරීමට අනුකලනය යන උසස් ගණිත ක්රමය භාවිතා කිරීමට සිදු වේ. එනිසා හැඩයන් කිහිපයක ආවස්ථික ඝූර්ණ කිහිපයක් පමණක් පහත පෙන්වන්නම්.
වස්තුවේ ආවස්ථික ඝූර්ණය කෝණික ත්වරණයෙන් වැඩි කළ විට ලැබෙන්නේ ව්යාවර්තයයි.
ව්යාවර්තය = (ආවස්ථික ඝූර්ණය) x (කෝණික ත්වරණය) (τ = Iα)
ඉහත වරහන තුළ පෙන්වා ඇත්තේ සංඛේතාත්මකව එය ප්රකාශ කරන අයුරුයි. (τ යනු ව්යාවර්ථයද, I යනු ආවස්ථික ඝූර්ණයද, α යනු කෝණික ත්වරණයද වේ.) මෙය F=ma යන සූත්රයට හරියටම අනුරූප වේ. රේඛිය චලිතයේ බලයට හිමි තැන කෝණික චලිතයේ හිමි වන්නේ ව්යාවර්තයට බව හොඳින් මතක තබා ගන්න. එනම්, යම් වස්තුවකට බලයක් යෙදීමෙන් එය රේඛියව චලනය කරන අතර, වස්තුවකට ව්යාවර්තයෙක් යෙදීමෙන් එය “කරකවයි” හෙවත් වෘත්ත චලිතයක යොදවයි. තවද, රේඛීය බලය (F) හා ව්යාවර්තය (τ) අතර පහත ආකාරයට සම්බන්ධයක් ඇත.
τ = Fr (ව්යාවර්තය = බලය x (කේන්ද්රයේ සිට බලය යොදන ලක්ෂ්යයට ඇති දුර ප්රමාණය))
වස්තුව ක්රමයෙන් වේගය වැඩි කර ගනිමින් කෝණිකව ගමන් කරන විට (එනම්, වස්තුව කෝණික ත්වරණියකින් ගමන් කරන විට), එම වස්තුවේ ගමන් මගෙහි යම් එක් ලක්ෂයක් පමණක් සලකා බලමු. එහිදී එම වස්තුවට පහත රූපයේ පෙන්වා දී ඇති ආකාරයට ස්පර්ශීය ත්වරණය (tangential acceleration), αt නම් රාශියක් අර්ථ දැක්විය හැකිය.
එම වස්තුවේ ගමන් මගෙහි (එනම් වෘත්තයේ පරිධියේ) ඕනෑම තැනකින් මෙම ස්පර්ශීය ත්වරණය මැනිය හැකිය. එම ත්වරණය හැම විටම කේන්ද්රයට ලම්භකවත් හා කැරකෙන දිශාව පැත්තටත් (රූපයේ පෙන්වා ඇති පරිදි) යොමුව පවතී.
ස්පර්ශීය ත්වරණය සේම ස්පර්ශීය ප්රවේගයද (tangential velocity) එලෙසම අර්ථ දැක්විය හැකියි. යම් වස්තුවක් ඒකාකාර කෝණික ප්රවේගයකින් (ත්වරණයකින් නොව) ගමන් කරන විට, මෙම ස්පර්ශීය ප්රවේගය වැදගත් රාශියකි. ඒ අනුව වෘත්ත චලිතයක යෙදෙන වස්තුවකට (සාමාන්ය) කෝණික ප්රවේගය මෙන්ම ස්පර්ශීය ප්රවේගය යන රාශි දෙකක් ගැන කතා කරන්න පුලුවන්. එවිතරක් නොවේ, ඒ දෙක අතර පහත සූත්රයෙන් පෙන්වා දෙන ආකාරයෙන් සම්බන්දතාවක්ද පවතී.
V = ωr (v යනු වස්තුවේ ස්පර්ශීය ප්රවේගය වන අතර, ω යනු එහි කෝණික ප්රවේගය වන අතර, r එම වස්තුව කේන්ද්රයේ සිට පවතින දුර ප්රමාණයයි.)
මෙම සූත්රය බැලූ බැල්මට ඔබට දෙයක් වටහා ගත හැකි විය යුතුය. එනම්, ස්පර්ශීය ප්රවේගය කේන්ද්රයෙන් ඈත් වන්නට වන්නට (r පදයෙන් කියන්නේ එයයි) වැඩි වේ. ඒ විතරක්ද නොවේ, වස්තුව කැරකෙන වේගය වැඩි වන විටද ස්පර්ශීය ප්රවේගය වැඩි වේ (ω පදයෙන් කියන්නේ එයයි). මෙය ඔබ නිතර අත් දැක තිබෙන දෙයක්. කැරකෙන රෝදයක් ගන්න. එය කරකවන්න. එක වටයක් කැරකුනාම ඔබ දන්නවා එම රෝදයේ සියලුම ස්ථාන අංශක360 ක් කැරකැවී නැවත හිටපු තැනට පැමිණි බව. එහෙත් ඔබ රෝදයේ කේන්ද්රයට ළඟින් හා දුරින් ලක්ෂ්ය දෙකක් සලකුණු කර රෝදය නැවත කරකවා බලන්න. ඔබට පේනවා ළඟින් ලකුණු කළ සලකුණට වඩා ඈතින් ලකුණු කළ සලකුණ වේගයෙන් කැරකැවෙනවා. ඉහත සූත්රයෙන් පෙන්වා දුන්නෙත් මෙයම තමයි.
වෘත්තාකාර තැටිය මතට (හරියමට කේන්ද්රය නොවන වෙනත් ඕනෑත තැනක) ගල් කැටයක් තබා එම තැටිය කැරකුවොත් කුමක් සිදු වේවිද? කැමති නම් ඔබට මෙය මෝටරයක් ගෙන මෙවැනි ඇටවුමක් පහසුවෙන්ම සාදා ගෙන මෙම පරීක්ෂණය සිදු කර බැලිය හැකියි. මෙලෙස තැබූ ගල අරීයව (radially) ඉවතට විසි වේ. (අරීය යන වචනයේ තේරුම වන්නේ වෘත්තයක ඇඳි අරයක් ඔස්සේය යන්නයි.) ඇත්තටම ගල අරීයව විසි වෙන්නේ අරීයව වුණත් අරීයව විසිවන බව දැකීමට ඔබටද එම තැටිය මත නැගීමට ගලත් සමගම කැරකීමට සිදු වෙනවා. ඔබ කැරකෙන තැටියෙන් පිටත සිට එම ගල විසි වෙන දෙස බලා සිටියොත් පෙනෙන්නේ ගල සර්පිලාකාරව (spiral) විසි වන බවකි පහත රූපයේ දැක්වෙන ලෙස. ඊට හේතුව ගලට අරීයව චලනයක් මෙන්ම රෝදය කැරකැවීම නිසා ඒ කැරකෙන දිශාවටද චලනයක් යන දෙයාකාරයේම චලනයක් එකවර තිබෙන නිසාය.
නිසලව තිබූ ගල යම් දෙසකට චලනය වන්නේ නම් විද්යාව අනුව ඔබ දන්නවා අනිවාර්යෙන්ම යම් බලයක් ඊට යෙදී තිබිය යුතු බව. එහෙත් ඔබ එවැනි බලයක් යෙදුවේද නැත ගල අරීයව ඉවත් කිරීමට. මෙම බලය අදෘෂ්යමාන බලයකි (fictitious force). සෑම රේඛිය නොවන චලිතයකම මෙම අදෘෂ්යමාන බලය ඇති වේ. එම බලය හැම විටම ක්රියාත්මක වන්නේ වෘත්තයේ කේන්ද්රයේ සිට අරීයව ඉන් ඉවතටයි. එමනිසා මෙම බලයට කේන්ද්රාපසාරි බලය (centrifugal force) යන නම ලැබී ඇත. මෙය බලය ඇති වන්නේ වස්තුවේ ස්කන්ධයට කේන්ද්රාපසාරි ත්වරණය ක්රියා කිරීමෙනි (බලයක් යනු නිව්ටන්ගේ දෙවන නියමය වන F=ma සූත්රය අනුව ස්කන්ධයක් වෙත ක්රියා කරන ත්වරණයක් සේ සැලකිය හැකියි).
මෙම කේන්ද්රාපසාරි ත්වරණය ගණනය කිරීමට සරල සූත්රයක්ද ඇත. එය නම්,
කේන්ද්රාපසාරි ත්වරණය = vω (v යනු වස්තුවේ ස්පර්ශීය ප්රවේගය වන අතර, ω යනු එහි කෝණික ප්රවේගයයි)
මෙයට ඉහත V = ωr යන සූත්රය ආදේශ කිරීමෙන් පහත ආකාරවලින්ද ලිවිය හැකිය.
(එනම්, කේ. ත්ව. = vω = v2/r = ω2r වේ. මේ කුමන හෝ පදයක් වස්තුවේ ස්කන්ධය වන m වලින් වැඩි කළ විට ලැබෙන්නේ කේන්ද්රාපසාරි බලයයි.)
මෙම කේන්ද්රාපසාරි බලයේ ඇති විශේෂත්වය වන්නේ වස්තුව ඒකකාර කෝණික ප්රවේගයකින් ගමන් කළත් කෝණික ත්වරණයකින් ගමන් කළත් මෙම බලය ඇති වීමයි (එහෙත් ඉහත කේන්ද්රාපසාරි ත්වරණය ගණනය කරන සූත්රය වලංගු වන්නේ ඒකාකාර කෝණික ප්රවේගයකින් ගමන් කරන වස්තුවකට පමණි. කෝණික ත්වරණයකින් යුතු වස්තුවක කෝණික ප්රවේගය මෙන්ම ස්පර්ශිය ප්රවේගයක නොකඩවා වැඩි වන නිසා, තත්වය තරමක් සංකීර්ණ වෙනවා එවිට එම සූත්රයට තරමක් උසස් ගණිත උපක්රමයක් භාවිතා කිරීමට සිදු වෙනවා). මෙයද නිව්ටන්ගේ නියමවලින්ම තේරුම්ගත හැකියි. බලයක් යෙදූ විට, වස්තුවේ ප්රවේගයේ හෝ ගමන් මගෙහි වෙනසක් සිදුවන බව නිවටන්ගේ පළමු නියමයෙන් කියැවේ. වෘත්ත චලිතයක් කියන්නේම අඛණ්ඩව වස්තුවේ දිශාව වෙනස් වන ආකාරයේ චලිතයකි. (එනිසානේ වස්තුව කේන්ද්රයක් වටා රවුමට ගමන් කරන්නෙ කෙලින් නොයා.)
ඉහත කේන්ද්රාපසාරි බලය උපයෝගි කරගෙන වැදගත් උපකරණ රාශියක් සාදා තිබෙනවා. ඔබේ ගෙදර ඇති වතුර පොම්පය ක්රියා කරන්නේ මෙම බලය උපයෝගි කරගෙනයි. ලේවල ඇති රතු රුධිර සෛල හා වෙනත් සංඝඨක වෙන් කරන්නේද මෙය උපයෝගි කරගෙනයි. කර්මාන්තශාලාවල දිග ලෝහ බට ආදායද මෙය භාවිතා කරමින් සිදු කරයි. එව්තරක් නොවේ, කානිවල්වල නිතර දක්නට ලැබෙන විශේෂාංගයක් වන “මාරක ළිඳ” ක්රියා කරන්නේද මේ නිසාය.
වස්තුව මොනම හෝ ආකාරයක වෘත්ත චලිතයේ යෙදෙන විට එහි ත්වරණයක් පවතින බව දැන් පැහැදිලියි. එම ත්වරණයේ එක් කොටසක් ඉහත සඳහන් ස්පර්ශීය ත්වරණය වන අතර, එහි අනෙක් කොටස කේන්ද්රාභාසාරි ත්වරණය (centripetal acceleration) ලෙස හැඳින් වෙනවා. කේන්ද්රාභිසාරි යන්නෙහි තේරුම කේන්ද්රය දෙසට යන්නයි. එනම්, මෙම ත්වරණය හැම විටම යොමු වන්නේ කේන්ද්රය දෙසටමයි. ස්පර්ශීය ත්වරණය නිසා වස්තුව චලනය වන අතර, කේන්ද්රාභිසාරි ත්වරණය නිසා එලෙස චලනය වන වස්තුව කේන්ද්රය දෙසට “ආකර්ෂණය වී පවතිනවා” (හෙවත් කේන්ද්රය දෙසට තල්ලු වෙනවා). මෙම ක්රියාවලි දෙකම එකට සිදුවන විට අපට එය දිස්වන්නේ වෘත්ත චලිතයක් ලෙසයි.
කේන්ද්රාභිසාරි ත්වරණයට වඩා කේන්ද්රාපසාරි බලය වැඩි වූ විට, වස්තුව කේන්ද්රය දෙසට එනවාට වඩා වැඩි පුර කේන්ද්රයෙන් ඉවතට යනවා. මෙය අපට දිස්වන්නේ ගල අරීයව විසි වෙනවා සේය. මෙම ත්වරණ දෙක හරියටම සමාන වූ විට පමණක්, ලස්සනට වෘත්තයක් සේ වස්තුව ගමන් කරනවා. කේන්ද්රාභිසාරි බලය අපසාරි බලයට වඩා වැඩි වූ විට වස්තුව ක්රමයෙන් (අරීයව) කේන්ද්රය දෙසට ඇතුලු වනවා.
අභ්යවකාශයේ රඳවන චන්ද්රිකා මෙන්ම, සූර්යා වටා ග්රහලෝක ගමන් කිරීමද, පොලොව වටා චන්ද්රයා ගමන් කිරීමද රැඳී පවතින්නේ ඉහත කී වෘත්ත චලිත නියම මතයි. සඳ පොලොවට ක්රම ක්රමයෙන් ළං නොවීද, ක්රම ක්රමයෙන් පොලොවෙන් ඉවත් නොවීද පවතින්නේ පොලොව හා චන්ද්රයා අතර පවතින ගුරුත්වාකර්ශණ බලයත් (මෙය කේන්ද්රාභිසාරි බලයයි.) චන්ද්රයා ගමන් වෘත්තාකාරව පොලොව වටේට ගමන් කිරීම නිසා ඇති වූ කේන්ද්රාපසාරි බලයත් යන දෙක ගාණට බැලන්ස් වීම නිසාය.
මේ ආකාරයටම කෝණික ගම්යතාව (angular momentum), p පහත දැක්වේ.
කෝණික ගම්යතාව = (අවස්ථිතික ඝූර්ණය) x (කෝණික ප්රවේගය)
මතක තබා ගන්න කෝණික චලිත සෑම අවස්ථාවකදීම ස්කන්ධය වෙනුවට යොදන්නේ අවස්ථිතික ඝූර්ණය බව.
වෘත්ත චලිත වැනිම තවත් චලිත විශේෂයකි භ්රමණ චලිත (rotational motion හෝ spin). වෘත්ත චලිතයකදී වස්තුව යම් කේන්ද්රයක් වටා වෘත්තයක පරිධියේ ගමන් කරන ආකාරයට චලනය වන අතර, භ්රමණ චලිතයකදී වස්තුව තමාගෙම අක්ෂය (axis) වටා කරකැවේ. මෝටරයක් කරකැවෙන දණ්ඩේ ඇත්තේ මෙවැනි භ්රමණ චලිතයකි. පොලොවද තම අක්ෂය වටා මෙලෙස භ්රමණය වන බව ඔබ දන්නවා.
මෙහිදීද කෝණික විස්ථාපනය, කෝණික ප්රවේගය, කෝණික ත්වරණය, කෝණික ගම්යතාව ආදිය එලෙසම භාවිතා වනවා පමණක් නොව, ඒවායේ සූත්රද වෘත්ත චලිතවලදී හමු වූ ඒවාමය. (නම්වලද ගැටලුවක් නැත. වෘත්ත ප්රවේගය, වෘත්ත ගම්යතාව ආදී ලෙස නම් යොදා තිබුණේ නම් පමණක්, අපට නමහි ගැටලු ඇති වීමට ඉඩ තිබුණා. එහෙත් කෝණික යන විශේෂණ පදය වෘත්ත හා භ්රමණ යන අවස්ථා දෙකටම එක ලෙස වලංගු බව පෙනේ. එනම්, මේ චලිත දෙකෙහිම අපට සැලකීමට සිදුවන්නේ කෝණයි.)
යම් වස්තුවක් කුමන හෝ ආකාරයක චලනයක් දක්වන විට, ඒ තුළ යම් ශක්තියක් පවතිනවා. එම ශක්තිය චාලක ශක්තිය (kinetic energy) ලෙස හැඳින්වෙනවා. රේඛීය චලිතයකදී චාලක ශක්තිය පහත සරල සූත්රයෙන් ගණනය කළ හැකියි.
චාලක ශක්තිය = (1/2)mv2 (m යනු වස්තුවේ ස්කන්ධය වන අතර v යනු එහි ප්රවේගයයි.)
වෘත්ත හෝ භ්රමණ චලිතයක යෙදෙන වස්තුවකදී පහත සූත්රය යොදාගත යුතුයි.
චාලක ශක්තිය = (1/2)Iω2 (I යනු වස්තුවේ අවස්තිථික ඝූර්ණය වන අතර ω යනු එහි කෝණික ප්රවේගයයි.)
යම් බලයක් තමන්ගේ බලය ක්රියාකරවන්නේ ක්ෂේත්රයක් (field) මගිනි. උදාහරණයක් ලෙස, ස්කන්ධයක් සහිත යම් පදාර්ථයක් විසින් ගුරුත්වාකර්ෂණ බලය ඒ අවට ඇති වෙනත් පදාර්ථවලට බලපාන පරිදි ක්රියා කරවන්නේ එහි ගුරුත්වාකර්ෂණ ක්ෂේත්රය මගිනි.
ක්ෂේත්රයක් වුවත් අවකාශය පුරා පැතිරී යන වේගයක් ඇති අතර එය ආලෝකයේ වේගයට සමානය. උදාහරණයක් ලෙස, ඈත පිහිටි සූර්යාගේ ගුරුත්වාකර්ෂණය විසින් අපේ පෘථිවිය ආකර්ෂණය කරගෙන ඇත. යම් ලෙසකින් සූර්යා ක්ෂණිකයෙන් අතුරුදහන් කළොත් සූර්යා නැති බව අප දැනගන්නේ විනාඩි අටකට විතර පසුවයි. ඊට හේතුව සූර්යාගේ බල ක්ෂේත්රයේ ඕනෑම වෙනසක් ගමන් කරන්නේ ආලෝකයේ වේගයෙන් නිසා, එම වේගයෙන් ගමන් කරන දෙයක් සූර්යා සිට පොලොවට ඇති දුර ප්රමාණය වන 150,000,000 km ගමන් කිරීමට විනාඩි අටකට ආසන්න කාලයක් ගත වේ. තවද, විදුලි ආරෝපණ මගින් විද්යුත් ක්ෂේත්රයක්ද (electric field), චුම්භක මගින් චුම්භක ක්ෂේත්රයක්ද (magnetic field) ගුරුත්වය විසින් ගුරුත්වාකර්ෂණ ක්ෂේත්රයක්ද (gravitational field) ආදී ලෙස ඒ ඒ බලයන් විසින් තමන්ගෙ ක්ෂේත්ර ඇති කරයි.
විශ්වයේ ඕනෑම තැනක ඇතිවන ඕනෑම වෙනස්කමක් වෙනත් තැනකට දැනගත හැක්කේ හෙවත් වෙනත් තැනකට සම්ප්රේෂණය විය හැකි උපරිම වේගය ආලෝකයේ වේගය බව හොඳින් මතක තබා ගන්න.
විද්යාවේදී හා තාක්ෂණයේදී විවිධ මිමි ගැනීම සිදුකරන්නේ මනින උපකරණ (measuring instruments/meters) ආධාරයෙනි. එලෙස මනින විට, මනින උපකරණයේ නිරවද්යතාවට (accuracy) වැඩි නිරවද්යතාවකින් යුතු මිම්මක් ඔබට ගත නොහැකිය. උදාහරණයක් ලෙස, ඔබ නිතර භාවිතා කරන අඩි රූල නම් දිගවල් මනින උපකරණය ගන්න.
එහි, එක පැත්තක cm 1, 2, 3 ආදී ලෙස සලකුණු කර ඇති අතර, ඒ දිග ඉරි දෙකක් අතර කෙටි ඉරිද පවතී. මෙම කෙටි ඉරි දෙකක් අතර පරතරය 1 mm කි. ඔබට මෙවැනි අඩි කෝදුවකින් මැනිය හැකි කුඩාම දිග කොච්චරද? ඉතා පැහැදිලිවම එය 1 mm වේ (මොකද කුඩා ඉරි දෙකක් අතර පරතරය 1mm ක් නිසා). මිලිමීටර් එකට වඩා කුඩා කිසිම අගයක් මින් නිවැරදිව මැන ගත නොහැකිය. ඊට හේතුව මෙම උපකරණයේ උපරිම නිරවද්යතාව මිලිමීටර් එකක් වීමයි. ඒ අනුව යම් වස්තුවක දිග ලෙස 4.23 cm ලෙස මෙම කෝදුවෙන් මැන ගත නොහැකිය මක්නිසාද යත් එම අගයේ දෙවැනි දශමස්ථානයෙන් කියන්නේ මිලිමීටරයෙනුත් දහයෙන් පංගු කොටස් (0.01mm)වේ. මෙය ඉතා සරල කාරණයක් බව ඔබට දැන් වැටහෙනවා. මීට වඩා නිවැරදිව දිගවල් මැනීමට අවශ්ය නම් කැලිපරය, මයික්රොමීටරය වැනි මනින උපකරණයක් භාවිතා කළ යුතු වෙනවා. එම උපකරණයටද මැනිය හැකි උපරිම නිරවද්යතාවක් පවතිනවා. ඇත්ත වශයෙන්ම අප භාවිතා කරන සෑම උපකරණයකටම මෙවැනි යම් උපරිම නිරවද්යතාවක් පවතිනවා.
පහත රූපය බලන්න. එහි එක පැත්තක් සරල අඩි කෝදුවකින්ද අනෙක් පැත්ත කැලිපරය වැනි උපකරණයකින්ද මැන ඇති බව සලකන්න. එසේ මැනගත් අගයන් රූපයේ දක්වා ඇත. කෝදුවෙන් මැනිය හැක්කේ 1mm (හෙවත් 0.1cm) ක උපරිම නිරවද්යතාවකින් බැවින් කෝදුවෙන් මැන ඇති සෙන්ටිමීටර් අගය දශමස්ථාන එකකට මැන ඇත. අනෙක් පැත්තේ දශමස්ථාන තුනකට නිවැරදිව මැන ඇත්තේ කැලිපරයේ නිරවද්යතාව දශමස්ථාන කිහිපයක් දක්වා යන බැවිනි.
දැන් මාගේ ප්රශ්නය එය නොවේ. මෙහි වර්ගඵලය කීයද? ඔබ පහසුවෙන්ම මෙවැනි චතුරස්රයක වර්ගඵලය දිග පළලින් වැඩි කර ලබා ගන්නවා. ඒ අනුව එහි වර්ගඵලය 7.534 x 3.4 = 25.6156 විය යුතුයි නේද? ඔව්. මෙම පිළිතුරේ දශමස්ථාන හතරක් තිබෙනවා. ඉන් කියන්නේ මෙය දශමස්ථාන හතරකට නිවැරදි කියාද? කොහෙත්ම එය සිදුවිය නොහැකිය. ඇයි? මෙහි උපරිම නිරවද්යතාව දශමස්ථාන තුනක් විය යුතුයි (මොකද දිග මැනගත් එක් උපකරණයක් වන කැලිපරයේ උපරිම නිරවද්යතාව එයයි. මැනගත් උපකරණයට වඩා නිවැරදිතාවක් කිසිසේත් තිබිය නොහැකියි නේද?). එසේ නම්, කිසිසේත් දශමස්ථාන හතරක නිවැරදිකමක් මෙම මනින උපකරණ ඔස්සේ ලබා ගත නොහැකියි. එහෙත් සාමාන්ය ගණිත නීතිය අනුව දශම සංඛ්යා දෙකක් ගුණ කරන විට, එහි අවසන් පිළිතුරෙහි එම සංඛ්යා දෙකෙහි තිබූ දශමස්ථානවල එකතුවට සමාන දශමස්ථාන ගණනක් තැබිය යුතු වෙනවා. ඉහත උදාහරණයේ එක සංඛ්යාවක දශමස්ථාන එකකත් අනෙක් සංඛ්යාවේ දශමස්ථාන තුනකුත් තිබුණ නිසා, එම සංඛ්යා දෙක ගුණ කළ විට, දශමස්ථාන හතරක් මේ අනුව තිබිය යුතුයි නේද? ඒ අනුව දශමස්ථාන හතරක් ලැබුණත් ඉහත පෙන්වා දුන් පරිදි ඉන් කියවෙන්නේ ප්රායෝගිකව හතරවන දශමස්ථානයෙන් කිසි පලක් නැති බව නොවේද? ඒ අනුව හතරවන දශමස්ථානය ඉවත් කර පිළිතුර 25.615 ලෙස දැක්විය හැකියි. එහෙත් මෙහිද යම් ප්රශ්නයක් තිබෙනවා. එනම්, ගුණ කරනු ලබන සංඛ්යා දෙකෙන් එක අගයක් දශමස්ථාන තුනකට නිවැරදි වුවත්, අනෙක් සංඛ්යාවේ නිරවද්යතාව තිබුණේ දශමස්ථාන එකකට පමණි. එමනිසා, වැඩි නිරවද්යතාවක් හා අඩු නිරවද්යතාවක් සහිත මෙවැනි සංඛ්යා දෙකක් යොදා ගුණ කිරීම (හෝ වෙනත් ගණිත කර්මයක්) සිදු කරන විට, අඩු නිරවද්යතාව සහිත සංඛ්යාවේ නිරවද්යතා ප්රමාණය (එනම් දශමස්ථාන ගණන) අවසන් පිළිතුරේ නිරවද්යතාව (එනම්, දශමස්ථාන ගණන) බවට ඉබේම පත් වෙනවා. ඉහත උදාහරණයේ අඩු නිරවද්යතාව සහිත සංඛ්යාව වනුයේ දශමස්ථාන එකක් ඇති අගයයි. මේ අනුව අවසන් පිළිතුර නිවැරදි විය යුත්තේ දශමස්ථාන එකකට පමණි. ඒ අනුව අවසන් පිළිතර දශමස්ථාන එකකට කෙටි කළ යුතුයි (25.6).
ඉහත කාරණාව හොඳින් මතක තබා ගන්න. ඔබ බොරුවට විශාල දශමස්ථානවලටම ගණන් සැදුවට වැඩක් නැහැ එහි නිරවද්යතාවක් නොමැති නම්. ඉහත පැහැදිලි කිරීම හැම විටම සිත්හි තබාගෙන ගණනය කිරීම කරන විට, අනවශ්ය ලෙස වැඩිපුර දශමස්ථාන සමග කටයුතු කිරීමද අවම වේ. මෙම තත්වය මා උපමාවකින් පවසන්නම්. හොඳ ශක්තිමත් පුරුක්වලින් සැදූ දම්වැලක් ගැන සිතන්න. එය ඉතා ශක්තිමත් වන අතර, ඇද්ද විට පහසුවෙන් කැඩී නොයයි. දැන් මෙම දම්වැලේ එක පුරුකක් ගලවා ඉතා බාල දුර්වල පුරුකක් එතැනට යොදන්න. දැන් දම්වැල පෙර සේම හයියෙන් ඇද්ද විට අර දුර්වල පුරුක ළඟින් කැඩී යයි. එනම්, හොඳ ශක්තිමත් පුරුක් දහස් ගණනක් ඇති දම්වැලක් වුවද එක් දුර්වල පුරුකක් පමණක් ඇත් නම්, එම දම්වැල කැඩිය හැකියි. මිමි ගැනීම ගැනද කිව යුත්තේ එයයි. උසස් ගණයේ උපකරණ ආශ්රයෙන් ඉතා ඉහළ නිරවද්යතා සහිත මිමි ගෙන, එහෙත් එකම එක අඩු නිරවද්යතාවක් සහිත මිම්මක් සහිත විට, අවසන් පිළිතුර නිවැරදි වන්නේ අර උසස් නිරවද්යාතවට නොව අර පහළ නිරවද්යතාවටයි.
තරංග
ඇත්තටම විවිධ හැඩයන්ගෙන් යුතු තරංග ඇත. සමහර විධිමත් හැඩයන්ට නම්ද ලබා දී ඇත. ඉහත හැඩය සයින් (හෝ සයිනාකාර (සයන් + ආකාර = සයිනාකාර)) යන නමින් හැඳින්වෙන අතර, අනෙක් විධිමත් හෝ අවිධිමත් සෑම හැඩයක්ම මෙම සයිනාකාර තරංගවල එකතුවක් ලෙස දැක්විය හැකිය. (එය සිදු කරන ගණිත ක්රියාවලිය Fourrier Transformation ලෙස හැඳින් වේ.) පහත දැක්වෙන්නේ විවිධ තරංග හැක කිහිපයක් වන අතර, මෙතැන් සිට අප කතා කරන්නේ සයින් තරංග ගැන පමණි.
විද්යාවේදී විවිධ දේවල් පැහැදිලි කිරීමේදී මෙම (සයින්) තරංග හැඩය ප්රයෝජනයට ගැනෙනවා. ඊට හේතුව විද්යාවේදී අප විද්යා න්යායන් හා රීතින් පැහැදිලි කරගැනීමට විවිධ ආකෘති භාවිතා කිරීමයි. එම ආකෘති රූපමය(graphical) ආකාරයටද බොහෝ විට දැක්වය හැකි නිසා, එම ආකෘතිවලින් කෙරෙන පැහැදිලි කිරීම් ඉතා පහසුවෙනුත් ඉකමනිනුත් නිවැරදිවයත් අවබෝධ කර ගත හැකියි. ඒ අනුව, මෙම තරංගද ආකෘතියක් (model) ලෙස වැදගත් වෙනවා යම් යම් විද්යාත්මක දේවල් පැහැදිලි කර ගැනීමට. එමනිසා, පළමුව සරලව තරංග ගැන පොදුවේ පැහැදිලි කර ගමු.
නිසල ජලාශයකට (ජලාශයක් අහල පහල නැතිනම්, වතුර පුරවපු බේසමක් හෝ මේ සඳහා ගත හැකියි.) කුඩා ගල් කැටයක් දමන්න. එවිට ජලය රවුමට රැළි නංවමින් ගමන් කරනවා.
මෙහිදී සිදු වන්නේ ගල වැටුණු ස්ථානයේ ජල මතුපිට පහළට එඹී ගොස් (උපරිම ප්රමාණයට පහළට ගිය පසු) නැවත ඉහළට එසවීමයි. එලෙස ඉහළට එසවෙන විට, එය සාමාන්ය පෙර තිබූ ජල පෘෂ්ඨයටද වඩා ඉහළට එස වේ. එසේ යා හැකි උපරිම ප්රමාණයට ඉහළට ගිය පසු නැවත පහළට ගමන් කරයි. මෙම සිදුවීම ගල වැටුණු තැන පමණක් නොව, ඒ අවට ප්රදේශයටද පැතිරී යයි. එනම්, ගල වැටුණු තැන පහළට එසවෙන විට, ඊට අවට රවුමක් වැනි පෙදෙසක් පෙර විස්තර කළ පරිදි උඩට එසවේ. එම රවුම උඩට එසවෙන විට, ඊටත් පිටත රවුමක් හැඩයට පෙදෙසෙහි ජල පෘෂ්ඨය පහළට යයි. මේ සිදුවීම රවුම් රවුම් ආකාරයට ගල වැටුණු තැන සිට වටේටම ”බෝ වේ” (පැතිරී යයි). මෙසේ ඇතිවන ජල රැළිවලට ජල තරංගයක් සේ කියයි. මෙය කොලයක යම් විධිමත් ආකාරයකට ඇන්ද විට ලැබෙන්නේ පහත ආකාරයේ රූපයකි.
මෙම තරංගය යැයි කියනා රූපය හා සත්ය ලෙසම ජලාශයේ ඇති වූ ජල තරංගය යන දෙකින්ම නිරූපණය වෙන්නේ එකම දෙය කියාද දැන් සොයා බලමු. ඉහත තරංගයේ A යනු රැලි නොමැති විට සංසුන්ව ඇති විට ජල පෘෂ්ඨය නිරූපණය වේ. දැන් ගල දැමූ විට කාලයත් සමග ක්රමයෙන් ජල මතුපිට පහළට යයි. A සිට B දක්වා එය නිරූපණය වේ. ජල පෘෂ්ඨය පහළට යන උපරිමය B යන්නෙන් නිරූපණය වේ. දැන් සිදුවන්නේ නැවත ජලය ක්රමයෙන් ඉහළට එස වීමයි. එවිට ජල කද සංසුන්ව තිබූ මට්ටම දක්වා විත් නවතින්නේ නැත. එම ස්ථානයද පාස් කරගෙන ඉහළට එස වේ. ප්රස්ථාරයේ B සිට C දක්වා කොටසින් පෙන්වනේ එයයි. දැන් ජලය උපරිම ඉහළ මට්ටමට පැමිණේ. C යනු එම ස්ථානයයි. දැන් නැවත ජල කද පහලට ක්රමයෙන් පැමිණේ. මෙය පහලට යන විට, ජලය නිසලව තිබූ මට්ටම පාස් කරගෙන නැවත පෙර සේම පහළට යා හැකි උපරිමය දක්වා ගමන් කරයි. මෙය C සිට Dදක්වා වූ කොටසින් නිරූපණය වේ. මේ ආකාරයට නොනවත්වා මෙම එකම දේ සිදු වේ. ඉතිං, ප්රස්ථාරයද නොනවත්වා එම හැඩයෙන්ම ඇඳිය හැකියි. තරංග ප්රස්ථාරයේ A සිට X දක්වා වූ හැඩය නැවත නැවත ඇති වන බව පෙනේ. එමනිසා, මුලු ප්රස්ථාරයම මුල සිට අග දක්වා අධ්යනය කරනු වෙනුවට අපට A සිට X දක්වා වූ කොටස පමණක් අධ්යනය කළ හැකියි නේද? එය කොතරම් පහසුවක්ද කියා ඔබට දැන් පේනවා.
තරංග ස්වභාවය අධ්යනය කිරීමට තවත් පහසු ක්රමයක් ඇත. ඒ සඳහා අවශ්ය වන්නේ නූලක් හා කුඩා බරකි. ඔබ නූලේ එක් කෙළවරකට කුඩා බරක් ගැට ගසන්න. දැන් එම නූලේ අනෙක් කෙළවරින් අල්ලාගෙන පළමු රූපයේ පෙනෙන සේ සිටින්න. දැන් අනෙක් අතින් එල්ලී තිබෙන බරට පොඩි තල්ලුවක් දී ඔරලෝසුවේ බට්ටා පැද්දෙන්නාක් සේ පැද්දෙන්නට සලස්වන්න. මෙම චලනය විද්යාවේදී සරල අනුවර්තී චලිතය (simple harmonic motion– SHM) ලෙස හැඳින්වෙන අතර, සෑම SHM එකක්ම තරංග ස්වාභාවයක් ගනී. ගල දෙපැත්තට උපරිම උසක් හෙවත් විස්ථාපනයක් (ඇත්තටම මෙය කෝණයකි) දක්වා ගමන් කරන අතර, මෙම උපරිම උසවල් දෙක අතර නොනවත්වාම එකම ආකාරයට චලනය සිදු වේ.
දැන් අප මෙම තරංගයක පවතින ලක්ෂණ ගැන ඉගෙන ගනිමු. විස්ථාරය (amplitude) යනු ශූන්ය මට්ටමේ සිට තරංගයේ උපරිම උස වේ. සාමාන්යයෙන් උඩු පැත්තට පවතින උපරිමය ධන උපරිමය ලෙසද, යට පැත්තට පවතින උපරිමය ඍණ උපරිමය ලෙසද සැලකිය හැකිය. තරංගයේ දිග තරංග ආයාමය (wavelength) ලෙස හැඳින්වේ. එය යම් තරංගයක උපරිම අගයේ (peak) සිට ඊ ළඟ උපරිම අගය දක්වා වූ දිග ලෙස හෝ අවම අගයේ සිට ඊ ළඟ අවමය දක්වා වූ දිග ලෙස හෝ තරංගයේ ඕනෑම තැනක සිට ඊ ළඟට හමු වන එවැනිම තැන දක්වා වූ දිග ලෙස සැලකිය හැකි බව පෙනේ.
ඉහත ජලාශ උදාහරණය ගැන නැවත සලකා බැලුවොත්, ජලය ඉහළට එසවෙන උපරිම මට්ටම ධන උපරිමය ලෙසද, ජලය පහළට යන උපරිම මට්ටම ඍණ උපරිමයද වේ. එලෙසම, ජලය ඉහළට උපරිමව එස වුණු එක වලල්ලක සිට, එලෙස උපරිම ලෙස ඉහළට එසවුණු ඊ ළඟ වලල්ලට ඇති දුර තරංග ආයාමය වේ.
ඉහත සරල අනුවර්තී චලිත උදාහරණයේදී, ගල එක පැත්තකින් එසවෙන උපරිම කෝණය (විස්ථාපනය) ධණ උපරිමය ලෙසත්, අනෙක් පැත්තට ගමන් කරන උපරිම කෝණය ඍණ උපරිමය ලෙසත් සැලකිය හැකියි. තරංග ආයාමයද ලැබෙන්නේ දිගක් ලෙස නොව කෝණයක් ලෙසය. එය අංශක 360කි හැමවිටම.
යම් තරංගයක් ආරම්භ වී එය අවසන් වන තෙක් යම් කාලයක් තුළ එය පවතී. තරංග ආයාමය යනු තරංගයේ දිග වන අතර, එම තරංග ආයාමය පෙන්වන හැඩයෙහිම එම තරංගය පවතින කාලයද නිරූපණය කළ හැකිය. එම කාලය ආවර්ථ කාලය (period) ලෙස හැඳින් වේ.
ප්රස්ථාරයේ එකම අක්ෂයේ (x අක්ෂය මත) තරංග ආයාමය සේම තරංග ආවර්ථයද එක විට නිරූපණය කළ හැකියි. එවිට, ආවර්ථය ගැන සලකන විට, එම අක්ෂය කාලයද; තරංග ආයාමය සලකන විට, එම අක්ෂයම දුරද (හෝ කෝණයද) නිරූපණය කරන බව සිහි තබා ගන්න. තවද, ඉහත ජලාශ උපමාව නැවත සැලකුවොත්, ජල තරංගය එක වලල්ලක් සෑදී ඊ ළඟ වලල්ල සෑදීමට ගතවන කාලය ආවර්ථය වේ. එක තත්පරයකට සෑදිය හැකි (හෝ පැවතිය හැකි) සම්පූර්ණ තරංග ගණන එම තරංගයේ සංඛ්යාතය (frequency) ලෙස හැඳින් වේ.
යම් තරංගයක් එක තැනක සිට තවත් තැනකට ගමන් කරනවා. එහෙත් එම ගමන් කිරීමේ යම් විශේෂත්වයක් තිබෙනවා. ඉහත ජලාශ උදාහරණයේදී ඔබ ගල අත හැරියේ පහළට වුවත්, ඉන් ඇති වූ රැලි හෙවත් ජල තරංග ගමන් කළේ ඔබ ගල අත හරින ලද දිශාවට නොව, හරහාටය. තරංගයක විශේෂත්වය මෙයයි. වස්තුව (මෙහිදී වස්තුව යනු ගල හෝ ගල වැටුණු ස්ථානයේ තිබූ ජල කොටස ලෙස මෙය සැලකිය හැකියි) හරහාට ගමන් නොකර එහෙත් එහි ශක්තිය හරහාට ගමන් කරවයි. මෙය හරියට පෝලිමට මිනිසුන් සිටගෙන ගඩොල් කැට අතින් අත පාස් කරමින් ගඩොල එක තැනක සිට වෙනත් තැනකට ගමන් කළාක් බදුය. ඔබ (එනම්, ගඩොල් පාස් කරන අය) ගමන් කරන්නේ නැතිව ගඩොල් පමණක් පාස් විය. එහෙත් ඔබ බෝලයක් වැනි දෙයක් බිම දිගේ රෝල් කර හැරිය විටකදී, ශක්තිය හරහාට ගමන් කරන්නේ බෝලයත් සමගමයි. මෙය හරියට ඔබ ගඩොල අතින් අරගෙන ඔබම ඇවිදගෙන ගොස් ගඩොල භාර දෙනවාක් බදුය. මේ අවස්ථා දෙකෙහි වෙනස වටහා ගන්න.
තරංගයක් ගමන් කරන වේගයක් ඇත. එය තරංග ප්රවේගය (wave velocity) ලෙස හැඳින් වෙනවා. තරංගයක ප්රවේගය, තරංග ආයාමය හා සංඛ්යාතය යන තුන එකිනෙකට සම්බන්ධ වේ. එය සූත්රයක් ආකාරයෙන් පහත ආකාරයට ලියයි.
V = fλ (v යනු තරංග ප්රවේගයද, f යනු සංඛ්යාතයද, λ යනු තරංග ආයාමයද වේ.)
ඕනෑම තරංගයකට ඉහත සූත්රය පොදු වේ. මෙම සූත්රය රූපමය ආකාරයටද තේරුම් ගත හැකියි. තරංගයක දිග λ නම්, තත්පරයකදී ඇතිවන තරංග ගණන f නම්, එම සියලු තරංගවල දිග (f x λ) වේ. මෙම fλ දිග එක තත්පරයකදී ඇතිවන දෙයකි. එක් තත්පරයකදී ගමන් කරන දුර ප්රමාණය ප්රවේගය ලෙස හඳුන්වන බව ඔබ දැන් දන්නවා. එමනිසා එම fλ යන්නෙන් නිරූපණය කරන්නේ එක් තත්පරයක් තුළ “තරංග සෙට් එකේ” මුලු දුර නිසා, මෙය තරංගයේ ප්රවේගය බව පැහැදිලියි නේද?
ජලාශය උපමාවෙන් තරංගය තේරුම්ගත් ඔබ දැන් තරංගය ඊට වඩා විද්යාත්මක ක්රමයෙන් තේරුම් ගනිමු. වෘත්ත චලිතය ගැන ඔබ පෙර ඉගෙන ගත්තා. එහිදීද අපට සංඛ්යාතය, ආයාමය, ආවර්ථය යන වචන හමු වූවා. එය අහම්බෙන් සිදු වූවක් නොවේ. වෘත්ත (හා භ්රමණ) චලිතය හා තරංග අතර ඇත්තේ නෑකමකි. පහත රූපය බලන්න.
ඉහත රූපයෙන් පැහැදිලිවම පෙනෙනවා යම් අංශුවක්/වස්තුවක් වෘත්තාකාරව ගමන් කරන විට, එය තරංග ස්වභාවයකින් දැක්විය හැකි බව. එක වටයක් (හෙවත් අංශක 360ක්) කැරකී අවසන් වන විට, ඉන් එක සම්පූර්ණ තරංගයක් නිරූපණය වෙනවා. තරංගයේ විස්තාරය යනු, වෘත්තයේ කේන්ද්රයේ සිට අංශුවට ඇති දුර හෙවත් වෘත්තයේ අරයයි. තරංගයේ සංඛ්යාතය යනු අංශුව තත්පරයකට කැරකෙන වට ගණනයි. ආවර්ථය යනු අංශුව එක වටයක් කැරකීමට ගන්නා කාලයයි. වෘත්ත චලිතයද මේ අනුව සරල අනුවර්තී චලිතයක් බව පැහැදිලියි.
උදාහරණ කිහිපයක් සලකා බලමු තරංග ආකෘතිය යොදා ගන්නා. පහත දැක්වෙන්නේ තරංගයක් බව ඔබ දන්නවා. මෙම තරංගය පීඩනය, විදුලි ධාරාව, වෝල්ටියතාව යන රාශින් තුන විස්තර කිරීමට යොදා ගන්නා අයුරු සලකා බලමු.
පළමුව පීඩනයට එය යොදන සැටි බලමු. ඉහත තරංගයෙන් නිරූපණය කරන්නේ යම් ස්ථානයකට ලැබෙන/දැනෙන පීඩනය යැයි සිතමු. තිරස් රේඛාවෙන් (x අක්ෂය) පෙන්වන්නේ කාලය යැයිද සිතන්න. ඒ අනුව, Aස්ථානයේදී තරංගයේ වක්රය පවතින්නේ ශූන්ය මට්ටමේය. එනම්, එම අවස්ථාවේදී පීඩනය ශූන්ය වේ. කාලය ක්රමයෙන් වැඩි වන විට, පීඩනය ක්රමයෙන් වැඩි වේ. දැන් B ස්ථානය ගැන සිතන්න. ඉන් කියන්නේ එම වෙලාව වන විට පීඩනය (සිරස් හෙවක් Y අක්ෂයෙන් දක්වා තිබෙන) යම් ප්රමාණයක් දක්වා වැඩි වී ඇති බවයි. කාලයත් සමග තව තවත් පීඩනය වැඩි වෙනවා උපරිම පීඩනය දක්වා. එම ස්ථානය C වලින් දක්වා ඇත. එලෙස, නැවත පීඩනය ක්රම ක්රමයෙන් ශූන්ය දක්වා අඩු වේ (D). ඉහතදී ශූන්යයේ සිට පීඩනය උපරිමය දක්වා වැඩි වී නැවත ශූන්යය දක්වා අඩු විය. එම කාලය මුලුල්ලේම එම පීඩනය අදාල ස්ථානයට යොමු වී තිබුණේ යම් දිශාවකටයි. (පහත පළමු රූපය බලන්න.) දැන් D සිට E දක්වා කොටසද පෙර සේම, පීඩනය ක්රමයෙන් වැඩි වී ශූන්ය දක්වා නැවත අඩු වේ. එහෙත් මෙම කොටසේදී ප්රස්ථාරයේ වක්රය පිහිටන්නේ x අක්ෂයෙන් පහළින්ය (මෙය ප්රස්ථාරයේ ඍණ කොටස වේ). ඉන් කියවෙන්නේ, x අක්ෂයෙන් ඉහළට පිහිටි කොටසේදී පීඩනය යොමු වී පැවතියේ යම් දිශාවකටද, එම දිශාවට විරුද්ධ දිශාවට දැන් පීඩනය යොමු වී පවතින බවයි.
දෙවනුව ඉහත තරංගයම විදුලි ධාරාව විස්තර කරන්නේ කෙලෙසදැයි බලමු. මෙයද පීඩනය විස්තර කළ පරිදිම කළ හැකියි. A නම් අවස්ථාව වන විට වයරයේ කිසිම පැත්තකට ධාරාවක් ගලා නොයයි (එනම් ධාරාවක් නැත). කාලය ක්රමයෙන් ගත වන විට ධාරාවද ටික ටික වැඩි වෙමින්ම වයරය දිගේ එක් පැත්තට ගමන් කරයි (A සිට B දක්වා). මෙලෙස C උපරිම ධාරා ප්රමාණය දක්වා මෙම ධාරාව ක්රමයෙන් වැඩි වේ. ඉන්පසු, නැවත ශූන්ය දක්වා ධාරාව ක්රමයෙන් අඩු වේ (C සිට D දක්වා). දැන් ධාරාව පෙර ගමන් කළ දිශාවට විරුද්ධ දිශාවට ගමන් කිරීම ආරම්භ කරනවා. එයද ශූන්යයේ සිට ක්රමයෙන් උපරිමයකට ගොස් නැවත ශූන්යය දක්වා අඩු වේ කාලයත් සමගම (Dසිට E දක්වා). ප්රස්ථාරයේ ඍණ කොටස හෙවත් දෙවැනි කොටසින් පෙන්වන්නේ මෙයයි. මෙය ඔබ ඉගෙන ගත් ඒසී විදුලි ධාරාව නේද?
ඉහත ආකාරයටම වෝල්ටියතාව ගැනද සිතා බලන්න. ශූන්ය මට්ටමේ සිට ක්රමයෙන් වෝල්ටියතාව උපරිමයකට ගොස් නැවත ශූන්ය බවට පත් වේ. ඉන්පසු, ඍණ කොටසේදී ධණ අග්රය ඍණද ඍණ අග්රය ධණ ලෙසද මාරු වී, නැවත ශූන්යයේ සිට උපරිමයටත් එතැනින් නැවත ශූන්යයටත් පැමිණේ.
ඉහත පෙන්වා දුන්නේ තරංගයක් ප්රායෝගිකව තේරුම් ගත යුතු ආකාරයයි. තරංගයේ x හා y අක්ෂ දෙකෙන් ඔබට සුදුසු රාශින් නිරූපණය කළ හැකියි. ඉහත උදාහරණ තුනෙහිම x අක්ෂයෙන් කාලය නිරූපණය කළා. එහෙත් උදාහරණ තුනෙහිම y අක්ෂයෙන් නිරූපණය කළේ වෙනත් රාශින් තුනකි. පළමු උදාහරණයේදී එය පීඩනයද, දෙවැනි උදාහරණයේදී ධාරා ප්රමාණයද, තෙවැනි උදාහරණයේදී වෝල්ටියතාවද y අක්ෂයෙන් නිරූපණය වූවා.
දෛශික (vector) රාශි යනු මොනවාදැයි දැනීමක් ඔබට අවශ්ය කෙරේ. ලෝකයේ බොහෝ දේවල් තිබෙනවා යම් කිසි අගයක් තිබෙන. උදාහරණ ලෙස, ඔබේ වයස, මේ මොහොතේ ඔබේ සාක්කුවේ තිබෙන මුදල් ප්රමාණය, ඔබේ වත්තේ තිබෙන අඹ ගසේ ඇති අඹ ගෙඩි ගණන ආදී අවස්ථා කිහිපය ගැන හිතන්න. මේ සෑම අවස්ථාවකදීම යම් කිසි අගයක් පැවසුවා. මේවායේ අගයන් කියන විට, ඔබට දිශාවක් ඒ සමග පැවසීමට අවශ්ය නැහැ. අවශ්ය නැහැ පමණක් නොව එවැනි අගයක් සමග දිශාවක් පැවසුවොත් ඔබව හාස්යයටද ලක් විය හැකියි. උදාහරණයක් ලෙස, මගේ වයස නැගෙනහිරට විස්සයි කියා කිව්වොත් එය විහිළුවක් බවට පත් වේ. මෙවැනි අගයක් පමණක් ඇති (හා එම අගයන් දිශාව අනුව වෙනස් නොවන) රාශින් අදිශ (scalar) රාශි ලෙස හැඳින් වේ.
එහෙත් සමහර රාශින් තිබෙනවා ඒවා පවසන විට දිශාවද වැදගත් වන. උදාහරණයක් ලෙස, ඉහත විස්තර කළ විස්ථාපනය, ප්රවේගය, ත්වරණය, බලය, ගම්යතාව ආදිය සමග හැමවිටම දිශාව වැදගත් වේ. මෙවැනි රාශි දෛශික ලෙස හැඳින් වේ. දෛශිකයක අගය දිශාව වෙනස් කරන විට වෙනස් වේ. උදාහරණයක් ගමු. ඔබ යම් දුරක් (මීටර් 100 ක්) උතුරු දිශාවට ගමන් ගත්තා යැයි සිතමු. එවිට, නැගෙනහිර දිශාවට ඔබේ ගමන සලකා බැලුවොත්, ඔබ නැගෙනහිර දෙසට ගමන් කර ඇති දුර බිංදුවයි. මේ අනුව දිශාව අනුව අගය වෙනස් වීම දෛශිකයක ස්වභාවයයි. එහෙත් කුමන දිශාවකට අනුව ගත්තත් ඔබේ වයස වෙනස් නොවේ. එනිසයි වයස අදිශයක් වූයේ.
අදිශ සමග ගණිතමය කර්ම (එකතු කිරීම, අඩු කිරීම, බෙදීම, වැඩි කිරීම ආදිය) සිදු කිරීම ඉතා පහසුය. සාමාන්ය සරල අංක ගණිතය ඒ සඳහා ප්රමාණවත්ය. ඒ අනුව, අදිශ රාශී දෙකක් අතර ඉතා පහසුවෙන් ගණිත කර්ම සිදු කළ හැකියි. එහෙත් දෛශික සමග ගණිත කර්ම සිදු කිරීම තරමක් සංකීර්ණ වේ. පළමුව මතක තබා ගන්න, දෛශික රාශියක් තවත් දෛශික රාශියකින් බෙදීම කළ නොහැකි බව. දෛශික රාශියක් තවත් දෛශික රාශියකින් ගුණ කරන විට, තිත් ගුණිතය (dot product) හා කතිර ගුණිතය (cross product) ලෙස දෙයාකාරයක වැඩි කිරීමේ අවස්ථා දෙකක්ද පවතිනවා (මෙවැනි තත්වයක් අදිශ දෙකක් ගුණ කිරීමේදි නැත). තවද, දෛශික දෙකක් එකතු කිරීමද සිදු කරන්නේ අමුතු ආකාරයකටයි (අඩු කිරීම යනුද එකතු කිරීමක් ලෙස සැලකිය හැකිය). එනිසාම එයට “දෛශික එකතු කිරීම හෙවත් දෛශික ආකලනය” (vector addition) කියා විශේෂ නමක්ද පවතිනවා. ගණිතය පිළිබඳ අතිරේකයෙන් මේ සියල්ල ගැන සලකා බලන නිසා මෙම අතිරේකයේ ඒ ගැන විස්තර කෙරෙන්නේ නැහැ.


















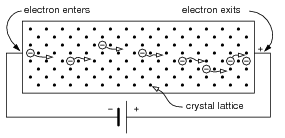










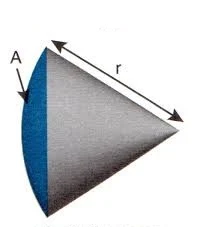



























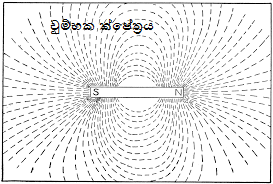
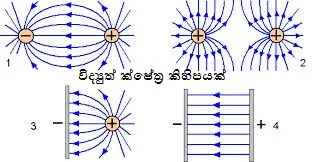




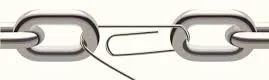











ගොඩාක් වටිනවා...........
ReplyDeleteස්තුතියි
i like electronics
ReplyDelete:) Learn and enjoy electronics... there are lots and lots of free and excellent resources on the internet and youtube.
ReplyDelete