Sourcing හා Sinking
යම් උපාංගයක
ඇති අග්රයක් තුලින් විදුලි
සංඥා/ධාරා
ගමන් කිරීම ගැන සිතන විට,
එය ආකාර
2කින්
පවතින බව පෙනේ.
එකක් නම්,
අග්රය
තුලින් පිටත සිට එම උපාංගය
තුලට ධාරාව ගමන් කිරීමයි.
මෙය තමයි
sinking (එහි
තේරුම “කිඳා බහිනවා” යන්නයි)
කියන්නේ.
අනෙක්
ආකාරය නම්,
අග්රය
තුලින් එම උපංගයේ සිට පිටතට
ධාරාව ගමන් කිරීමයි.
මෙය
sourcing (එහි
තේරුම “සපයනවා” යන්නයි)
ලෙස
හැඳින්වේ.
ඉතිං
ට්රාන්සිස්ටරයක අවුට්පුට්
අග්රය මේ ආකාර දෙකෙන් එක්
ආකාරයක් ගත යුතුයි.
සින්කිං
සිදු වන්නේ ට්රාන්සිස්ටර්
අග්රය මත පවතින වෝල්ටියතාව
එම අග්රය සම්බන්දව පවතින
අනෙක් කොටසට වඩා වැඩි වන විටයි;
එවිටනෙ
වැඩි වෝල්ටියතාවේ සිට අඩු
වෝල්ටියතාව පවතින තැන දක්වා
ධාරාව ගලන්නේ (“ධාරාව
සින්ක් වේ”).
එලෙසම,
ට්රාන්සිස්ටර්
අග්රය මත පවතින වෝල්ටියතාව
එය සම්බන්ධිත අනෙක් තැනට වඩා
වැඩි වන විට ට්රාන්සිස්ටරයේ
සිට අනෙක් ස්ථානයට ධාරාව ගලයි
(“ධාරාව
සෝස් වේ”).
උදාහරණයක්
ලෙස, කොමන්
එමිටර් වින්යාසය එන්පීඑන්
ට්රාන්සිස්ටරයක් යොදා ගෙන
භාවිතා කරන විට,
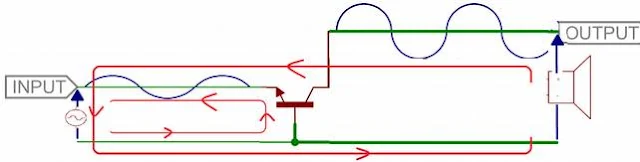
ඉහත රූපයේ
(අ)
හි දැක්වෙන
පරිදි ඉන්පුට් කරන සංඥා ධාරාවට
අනුරූපව විචලනය වන කලෙක්ටර්
ධාරාවක් අවුට්පුට් පරිපථයේ
ඇති වන අතර,
එම කලෙක්ටර්
ධාරාව සැපයුමේ වෝල්ටියතාවේ
(A) සිට
කලෙක්ටරය (B)
තුලට
සින්ක් වේ.
එහෙත්
කොමන් එමිටර් වින්යාසය
පීඑන්පී ට්රාන්සිස්ටරයක්
යොදා ගෙන භාවිතා කරන විට,
එම කලෙක්ටර්
ධාරාව කලෙක්ටරයේ සිට ගමන්
කරන (සෝස්
වන බව) ඉහත
රූපයේ (ආ)
මඟින්
පෙනේ.
සෝස් හෝ
සින්ක් වීම සංඥාවේ ක්රියාකාරිත්වයන්
සඳහා එතරම් වැදගත්කමක් නැත.
එනිසා
පරිපථ විස්තර කිරීම්වලදී
සෝස් වීම හෝ සින්ක් වීම ගැන
නොසිතා අහවල් අග්රය හරහා
සංඥා ගමන් කරනවා යනුවෙන් පමණක්
සඳහන් කිරීම බොහෝවිට සිදු
වේ. එනිසා
කොමන් එමිටර් වින්යාසය විස්තර
කරන විට,
අවුට්පුට්
ධාරාව/සංඥාව
කලෙක්ටරය හරහා ගමන් කරයි
යනුවෙන් හෝ කලෙක්ටර් ධාරාව
එමිටරය හරහා පථය සම්පූර්ණ කර
ගනියි යනුවෙන් හෝ පැවසිය
හැකියි.
කොමන් බේස් වින්යාසය
මෙහිදී බේස්
අග්රය පොදු වන අතර,
එමිටර්
අග්රය ඉන්පුට් අග්රය ලෙසද
කලෙක්ටරය අවුට්පුට් අග්රය
ලෙසද ක්රියාත්මක වේ.
වර්ධනය
(ධාරාවේ,
වෝල්ටියතාවේ,
ජවයේ),
ඉන්පුට්
ඉම්පීඩන්ස්,
අවුට්පුට්
ඉම්පීඩන්ස් ගැන කෙටියෙන්
සොයා බලමු.
ඉන්පුට්
ධාරාව එමිටරයෙන් ඇතුලුවී
බේසය හරහා පථය සම්පූර්ණ කර
ගනී. ඔබ
දන්නවා ක්රියාකාරීව පවතින
හෙවත් බයස් කරපු ට්රාන්සිස්ටරයක
බේස්-එමිටර්
ඩයෝඩය පෙරනැඹුරුවයි පවතින්නේ.
එවිට එම
ගමන් මාර්ගයේ ප්රතිරෝධය
අඩුය. ඒ
අනුව,
ඉන්පුට්
ඉම්පීඩන්ස් අගය ඕම් කිහිපයක්
තරම් කුඩා අගයක් ගනී.
අවුට්පුට්
ධාරාව “කලෙක්ටර්-බේස්
සන්ධිය හරහා” ගොස් එමිටරය
හරහාද ගමන් කරයි.
මින්
පෙරත් විස්තර කළ පරිදි
කලෙක්ටර්-බේස්
කොටස පසුනැඹුරු වන අතර එනිසා
මෙම වින්යාසයේදී අවුට්පුට්
ඉම්පීඩන්ස් අගය විශාල වේ.
වර්ධනය ගැන
බලමු. ධාරා
වර්ධනය වනුයේ (කලෙක්ටර්
ධාරාව)
/ (එමිටර්
ධාරාව)
වේ.
දළ වශයෙන්
එම ධාරා දෙක සමානය (iE
= iC + iB වන
අතර, බේස්
ධාරාව ඉතා කුඩා වේ).
ඒ අනුව
පෙනෙනවා මෙම වින්යාසයේදී
ධාරා වර්ධනය 1ට
ආසන්නව 1ට
අඩු අගයක් බව.
කලෙක්ටර්
ධාරාව හා එමිටර් ධාරාව අතර
අනුපාතය α
යන සංඛේතයෙන්ද
හඳුන්වනවා (හරියට
කලෙක්ටර් ධාරාව හා බේස් ධාරාව
අතර අනුපාතය බීටා අකුරෙන්
සංඛේතවත් කළා සේ).
ඇල්ෆා හා
බීටා අතරද පහත ආකාරයට සම්බන්දතාවක්
ගොඩනැඟිය හැකිය.
ධාරා වර්ධනයක්
නොමැති වුවත්,
වෝල්ටියතා
වර්ධනයක් ඇත.
ඊට හේතුව,
ඉන්පුට්
ඉම්පීඩන්ස් අගයට වඩා විශාල
අවුට්පුට් ඉම්පීඩන්ස් අගයක්
පැවතීමයි.
පහත රූපයෙන්
පෙන්වා තිබෙන්නේ වෝල්ටියතා
වර්ධනය ව්යුත්පන්න කර අවසන්
නිගමනයට එළැඹෙන ආකාරය කෙටි
සංඛේත මඟින්.
ඔබ මෙවැනි
කෙටි සංඛේතවලට හොඳින් හුරු
විය යුතුය.
වෝල්ටියතා
වර්ධනය යනු අවුට්පුට් වෝල්ටියතාව
හා ඉන්පුට් වෝල්ටියතාව අතර
අනුපාතයයි.
ඉන්පුට්
ධාරාව වන කලෙක්ටර් ධාරාව
ඉන්පුට් ඉම්පීඩන්ස් අගයෙන්
වැඩි කළ විට (ඕම්
නියමය අනුව)
ඉන්පුට්
වෝල්ටියතාවත්,
එලෙසම
අවුට්පුට් ධාරාව වන කලෙක්ටර්
ධාරාව අවුට්පුට් ඉම්පීඩන්ස්
අගයෙන් වැඩි කළ විට අවුට්පුට්
වෝල්ටියතාවත් ලැබේ.
එවිට,
ධාරා
අනුපාතය වෙනම සලකා,
එය පෙර
උගත් ඇල්ෆාට සමාන වන නිසා
ඇල්ෆා ආදේශ කර ඇත.
එම අගය
දළ වශයෙන් 1
යිනෙ.
එවිට
අවසානයේ වෝල්ටියතා වර්ධනය
යනු අවුට්පුට් ඉම්පීඩන්ස්
හා ඉන්පුට් ඉම්පීඩන්ස් දෙක
අතර අනුපාතයට සමාන වේ.
ඉතිං,
කොමන්
බේස් වින්යාසයේදී අවුට්පුට්
ඉම්පීඩන්ස් අගය විශාල බවත්,
ඉන්පුට්
ඉම්පීඩන්ස් අගය කුඩා බවත්
දැනගත් නිසා,
එම අනුපාතය
විශාල සංඛ්යාවකි;
එය 1ට
වඩා බොහෝ විශාල බව ඉහත සංඛේත
ක්රමයෙන් දක්වා තිබේ.
එලෙසම ජව
වර්ධනයත් පහත ආකාරයට දැක්විය
හැකිය.
එය කියවා
තේරුම් ගන්න.
ඇල්ෆා
හි වර්ගය ආසන්න වශයෙන් 1
වේ (එහෙත්
ඇත්ත වශයෙන්ම ඇල්ෆා 0.98ක්
වැනි දශම අගයකි;
එනිසා
0.982 =
0.96 පමණ
වේ). ඒ
අනුව ජව වර්ධන අගය වෝල්ටියතා
වර්ධන අගයට වඩා ඉතා ටිකක්
අඩුය.
උදාහරණයක්
ලෙස,
වෝල්ටියතා
වර්ධනය 98ක්
නම්, ජව
වර්ධන අගය 96ක්
පමණ වේ.
ඉහත විස්තර
අනුව පෙනෙනවා කොමන් බේස්
වින්යාසයේදී ධාරා වර්ධනයක්
නොලැබෙන බවත්,
වෝල්ටියතා
හා ජව වර්ධනයන් පවතින බවත්.
එහෙත්
එම අගයන්ද පොදු විමෝචක
වින්යාසයේදී ලැබුණු අගයන්ට
වඩා අඩුය.
තවද,
අවුට්පුට්
වෝල්ටියතා සංඥාව අපවර්තනය
නොවේ.
කොමන් කලෙක්ටර් වින්යාසය
ඉන්පුට්
අග්රය බේසය වන අතර,
අවුට්පුට්
අග්රය එමිටරය වේ.
පොදු
අග්රය කලෙක්ටරය වේ.
මෙවිට,
ඉන්පුට්
ධාරාව බේස්-කලෙක්ටර්
හරහා පවතින බවත්,
අවුට්පුට්
ධාරාව එමිටර්-කලෙක්ටර්
හරහා පවතින බවත් පෙනේ.
ඉන්පුට්
ඉම්පීඩන්ස් අගය විශාල වේ.
මෙතෙක්
සලකා බැලූ වින්යාස 3න්
ඇත්තටම මෙම වින්යාසයේ තමයි
ඉහල ඉන්පුට් ඉම්පීඩන්ස් අගයක්
පවතින්නේ.
මෙම
වින්යාසයේ තිබෙන ලොකුම වාසියද
එයයි. ඊට
හේතුව,
ඉන්පුට්
ධාරාව ගලා යන්නේ බේස්-කලෙක්ටර්
සන්ධිය හරහාය;
එය පසුනැඹුරු
වේ. ඔබ
දැන් අසාවි කොහොමද පසුනැඹුරු
සන්ධියක් හරහා ධාරාවක් ගලා
යන්නේ කියා.
එම ධාරාව
ඇත්තටම ගලා යෑමට හැකියාව
තිබෙන්නේ එමිටරය හරහා තමයි.
එහෙත්
එය සාපෙක්ෂවයි බැලිය යුත්තේ.
එමිටර්-කලෙක්ටර්
හරහා අවුට්පුට් ධාරාව ගලා යන
නිසා,
අවුට්පුට්
ඉම්පීඩන්ස් යනු එම කොටසේ
ප්රතිරෝධ අගය වේ.
එයත් පෙර
සේම පසුනැඹුරු කලෙක්ටර්-බේස්ද
ඇතුලත් කොටසක් නිසා ප්රතිරෝධ
අගය ඉහලය (ට්රාන්සිස්ටර්
ක්රියාව නිසා පමණක් එමිටර්/කලෙක්ටර්
ධාරාව ගලා යයි).
ධාරා වර්ධනය
පහත ආකාරයට වේ.
එය ආසන්න
වශයෙන් බීටා අගයට සමාන වන අතර,
එය විශාල
අගයකි. ඒ
කියන්නේ මෙම වින්යාසයේදී
විශාල ධාරා වර්ධනයක් ලැබේ.
වෝල්ටියතා
වර්ධනයද ගණනය කරමු.
දළ වශයෙන්
කලෙක්ටර් ධාරාව හා එමිටර්
ධාරාව සමාන නිසා එම අනුපාතය
1 ලෙස
සැලකිය හැකියි (එහෙත්
ඇත්තටම එම අගය බිංදුවයි දශම
නවයයි ගණනකි).
ප්රායෝගික
මැනබැලීම්වලදී ප්රතිදාන
ඉම්පීඩන්ස් එක හා ප්රදාන
ඉම්පීඩන්ස් එක දළ වශයෙන් සමාන
වේ. එවිට,
එම අනුපාතයද
1 ලෙස
ගත හැකිය.
ඒ අනුව
පෙනෙනවා පොදු සංග්රහක
වින්යාසයේදී වෝල්ටියතා
වර්ධනයක් නැති බව.
බේසයට ඉන්පුට්
කරන සංඥා වෝල්ටියතාවම වර්ධනය
නොවී එමිටරයෙන් පිට වේ.
එනිසා
එම වින්යාසය emitter
follower යන
නමින්ද හැඳින්වෙනවා.
තවද,
යම් ඇක්ටිව්
උපාංගයක් විසින් ඊට ඇතුලු කළ
වෝල්ටියතාව වර්ධනය හෝ හායනය
නොකර එලෙසමම පිට කරන විට,
ඊට buffer
යන නම
යෙදෙනවා.
ඒ අනුව
පොදු සංග්රහක වින්යාසයේ
ක්රියාත්මක කරවන ට්රාන්සිස්ටරය
බෆර් එකකි.
අවුට්පුට්
වෝල්ටියතා සංඥාව අපවර්තනය
නොවේ.
ජව වර්ධනය
යනු වෝල්ටියතා වර්ධනය ධාරා
වර්ධනයෙන් ගුණ කිරීමෙන් ලැබෙන
අගයට සමාන නිසා,
මෙම
වින්යාසයේදී වෝල්ටියතා
වර්ධනය ආසන්න වශයෙන් 1
නිසාත්,
ධාරා
වර්ධනය බීටා අගයට සමාන නිසාත්,
ජව වර්ධනයද
1 x β = β වේ.
ඉහත ආකාරයට
අප වින්යාස 3හිම
ප්රධාන ලක්ෂණ/පරාමිතින්
පහත ආකාරයට සංක්ෂිප්ත කළ
හැකිය. ඒ
කතා කළ විස්තරයන්ට අමතරව තවත්
විශේෂිත ගති ලක්ෂණද ඇති අතර
පසුවට ඒවා කතා කරමු.
සංඥා
සංඛ්යාතය වැඩි වන විට එම
විශේෂිත ගති ලක්ෂණවල වැදගත්කමද
වැඩි වේ.
|
|
කොමන්
එමිටර්
|
කොමන්
කලෙක්ටර්
|
කොමන්
බේස්
|
|
ඉන්පුට්
ඉම්පීඩන්ස්
|
ඉතා
අඩුය
|
වැඩිය
|
ඉතා
අඩුය
|
|
අවුට්පුට්
ඉම්පීඩන්ස්
|
ඉතා
වැඩිය
|
වැඩිය
|
ඉතා
වැඩිය
|
|
ධාරා
වර්ධනය
|
ඉතා
වැඩිය
|
1
|
ඉතා
වැඩිය
|
|
වෝල්ටියතා
වර්ධනය
|
ඉතා
ඉතා වැඩිය
|
ඉතා
වැඩිය
|
1
|
|
ජව
වර්ධනය
|
ඉතා
ඉතා ඉතා වැඩිය
|
ඉතා
වැඩිය
|
ඉතා
වැඩිය
|
|
අපවර්තනය
|
ඇත
|
නැත
|
නැත
|
ඉහත සියලු
වින්යාස විස්තර කිරීමේදී
යම් සරල කිරීමක් සිදු කර ඇත.
එනම්,
එම ට්රාන්සිස්ටර්
බයස් කර නැත (එහෙමත්
නැතිනම්, බයසිං
පරිපථ කොටස් පෙන්වා නැත).
එය උවමනාවෙන්ම
සිදු කරන ලද්දක් වන අතර ඊට
හේතුව එම පරිපථ කොටස්ද (රෙසිස්ටර්)
පෙන්වන්නට
ගියොත් පැහැදිලි කිරීම තරමක්
සංකීර්ණ වේ. තවද,
බයසිං කරන
ක්රම කිහිපයක්ම පවතින නිසා,
ඒ එක් එක්
බයසිං ක්රමයට අනුව පැහැදිලි
කිරීමද වෙනස් වී සංකීර්ණතාව
තවත් වැඩි වේවි. එහෙත්
වඩාත්ම යෝග්ය ක්රමය ලෙස මා
සිතන්නේ බයසිං පරිපථ නැතිව
ඉහත ආකාරයට විශ්ලේෂනය කර ඒ
ලබා ගත් දැනුම සමඟ බයසිං පරිපථ
කොටස්ද සහිතව ට්රාන්සිස්ටර්
වින්යාස ගැන පහසුවෙන් අධ්යනය
කළ හැකි බවයි. මොහොතකින්
ඒ ගැනත් අප විස්තරාත්මකව සලකා
බලනවා.

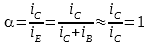





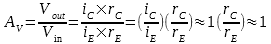
නොමිලේ ගන්න පුළුවන් හොඳම VPN සේවාව මොකක්ද?
ReplyDeleteTor බ්රව්සරය පාවිච්චි කරන්නේ කොහොමද?
VPN නිසා වැඩියෙන් ඩේටා කැපෙනවද?
මා පෞද්ගලිකවම වසර ගණනාවක් තිස්සේ (වරින් වර) භාවිතා කරන වීපීඑන් සේවාව vpnbook.com වේ. මුල සිටම එය මගේ වැඩවලට ඕනවටත් වඩා හොඳ සේවාවක් වූ බැවින් හොඳම එක කුමක්දැයි මට සැසඳීමට බැරිය. වීපීඑන් නිසා ඩේටා කැපෙන්නේ නැත අමුතුවෙන්... සාමාන්යයෙන් කැපෙන ටික කැපේවි... එහෙත් වීපීඑන් කනෙක්ෂන් එකේදී UDP ප්රෝටොකෝලය තෝරා ගත හැකි නම් (vpnbook.com හි එම තෝරාගැනීමේ හැකියාව ඇත) දත්ත වැඩියෙන් නොව අඩුවෙන් කැපේවි (තාක්ෂණිකව සලකා බැලුවොත්).
Deleteටෝර් බ්රවුසරය ගැන මට දැනුමක් නැත (එය භාවිතා කිරීමට අවශ්යතාවක් තිබී නැති නිසා). මා භාවිතා කරන්නේ ෆයර්ෆොක්ස් පමණකි...