ෆීඩ්බැක් බයස් ක්රමය යෙදූ කොමන් එමිටර් වින්යාසය
දැන්
ෆීඩ්බැක් බයස් ක්රමය යොදා
ගෙන බලමු.
මෙය
collector
feedback biasing හෝ
collector-to-base
biasing ලෙසද
හඳුන්වනවා.
ෆීඩ්බැක්
බයස් ක්රමයේදී ට්රාන්සිස්ටරයේ
බේසයට අවශ්ය බයස් වෝල්ටියතාව
ලබා ගන්නේ එම ට්රාන්සිස්ටරයේම
කලෙක්ටර් අග්රයෙන් ලබා ගන්නා
විදුලියෙනි.
කලෙක්ටරයෙන්
බේසයට අවශ්ය ඉතා කුඩා බේස්
ධාරාව (ප්රතිපෝෂන
ධාරාව – feedback
current – IF ලෙස
මෙම ධාරාව හැඳින්වේ)
උකහා ගෙන,
එය ෆීඩ්බැක්
රෙසිස්ටරය (RF)
හරහා
යවනවා.
එවිට,
RF රෙසිස්ටරය
හරහා යම් වෝල්ටියතාවක් පාතනය
වන අතර එම වෝල්ටියතාව ප්රතිපෝෂන
වෝල්ටියතාව – feedback
voltage – VF ලෙස
හැඳින්වේ.
එම IF
ධාරාව
බේස්-එමිටර්
කොටස හරහා භූගත වේ.
ඉහත
ඡේදයේ හා රූපයේ දැක්වෙන පරිදි
එතැන තිබෙන්නේ කරන්ට් ෂන්ට්
ෆීඩ්බැක් එකකි.
එය නෙගටිව්
ෆීඩ්බැක් එකක්ද වේ.
වැඩි
විස්තර කිරීම් නැතිවම මෙම
ෆීඩ්බැක් එක නෙගටිව් බව පහසු
ක්රමයකින් පෙන්වා දිය හැකිය.
ට්රාන්සිස්ටරයේ
වෝල්ටියතා අපවර්තනයක් සිදු
වේ (කොමන්
එමිටර් වින්යාසය නිසා).
ඉතිං,
කලෙක්ටරය
හා බේසය අතර පවතින්නේ එකිනෙකට
විරුද්ධ සම්බන්දතාවක් (එනම්,
බේසය මත
වෝල්ටියතාව උඩට යන විට කලෙක්ටර්
වෝල්ටියතාව යටට යයි).
එවිට යම්
සංඥාවක් ගමන් කරන මාර්ගයක
එකිනෙකට විරුද්ධ ස්ථාන දෙක
ඍජුව සම්බන්ද කළ විට ඇති
වන්නේ නෙගටිව් ෆීඩ්බැක් එකක්.
සටහන
(නෙගටිව්)
ෆීඩ්බැක්
එකක් ඇති විට අනිවාර්යෙන්ම
එය ට්රාන්සිස්ටරයේ ඉන්පුට්
ඉම්පිඩන්ස් එකට ඍජු බලපෑමක්
ඇති කරයි.
එම ෆීඩ්බැක්
එක මික්ස් කරන්නේ සීරීස්
ආකාරයට නම් ඉන්පුට් ඉම්පිඩන්ස්
අගය ඉහල යන අතර,
මික්ස්
කරන්නේ ෂන්ට් ආකාරයට නම්
ඉන්පුට් ඉම්පිඩන්ස් අගය පහල
යයි. එනිසා
මින් පෙර අප ඉගෙන ගත් එමිටර්
රෙසිස්ටරයක් යෙදූ අවස්ථාවේදී
එය සීරීස් ආකාරයක් නිසා,
එවිට
ඉන්පුට් ඉම්පිඩන්ස් අගය වැඩි
වූ බව මතක් කර බලන්න;
එහිදී
(β + 1)re
වෙනුවට
(β +1)(re
+ RE) වූවා.
තවද,
දැන් අප
සලකා බලන ෆීඩ්බැක් බයස්
ක්රමයේදී මික්ස් වන්නේ ෂන්ට්
ආකාරයට බැවින් ඉන්පුට්
ඉම්පිඩන්ස් එක අඩු වන බව මතක
තබා ගන්න.
එනිසා,
මෙම
ෆීඩ්බැක් ක්රමය භාවිතා කරන
වර්ධකය shunt
feedback amplifier යනුවෙන්ද
හඳුන්වනවා.
කෙසේ
වෙතත්,
නෙගටිව්
හෝ පොසිටිව් ෆීඩ්බැක්ද යන වග
නොසලකා යම් විදුලි ප්රමාණයක්
කලෙක්ටරයෙන් උකහා ගෙන බේසයට
ලබා දීමක් ලෙස සිතුවාට මෙහි
වරදක් නැත.
නිවාත
අගයන් ඉතිං ඉහල හෝ පහල යෑම
සිදු වන්නේ නැහැනේ සෛද්ධාන්තිකව
ගත් විට.
එසේ වුවත්,
ප්රායෝගිකව
බලන විට,
උෂ්ණත්වය
ආදී සාධක මත ට්රාන්සිස්ටරයේ
β වැනි
පරාමිතින් විචලනය වී එමඟින්
නිවාත අගයන් එහා මෙහා යනවා.
එම විචලනය
වුවද ක්ෂණික නොවේ (සංඥාවලදී
තමයි ක්ෂණික විචලනයන් පවතින්නේ).
එවැනි
අවස්ථාවලදී,
මෙතැන
ඇත්තටම නෙගටිව් ෆීඩ්බැක්
එකක් ඇති නිසා,
මීට පෙර
අප කතා කළ වාසි ඉබේම මෙම ෆීඩ්බැක්
බයස් ක්රමයේ ඇත.
ගණනය
කිරීම්වලට යෑමට පෙර එක් වැදගත්
කරුණක් මුලින්ම අප ඉගෙන ගමු.
ඒ RIN
නම්
රෙසිස්ටරය ගැනයි.
මීට පෙර
ඉන්පුට් රෙසිස්ටර් පාඩමේදී
මේ ගැන තවදුරටත් පැහැදිලි
කරන බවට මා පොරොන්දු වුණා.
ඇත්තටම
ෆීඩ්බැක් බයස් ක්රමය යොදා
ගන්නා විට ඉන්පුට් රෙසිස්ටරයක්
අත්යවශ්ය යැයි සිතුවට වරදක්
නැත. යොදා
ඇති RF
නම්
ෆීඩ්බැක් රෙසිස්ටරය මඟින්
ඩීසී/නිවාත
විදුලිය මෙන්ම ඒසී/සංඥා
විදුලියද ෆීඩ්බැක් කෙරේ.
RIN නොතිබුණා
නම්, මෙලෙස
ෆීඩ්බැක් වන ඒසී/සංඥා
විදුලි ධාරාව ට්රාන්සිස්ටරයේ
බේසය හරහා භූගතයට නොගොස් සංඥා
ප්රභවය හරහා ගොස් භූගත විය
හැකිය (සම්පූර්ණ
ධාරාවම නොවුණත් සැලකිය යුතු
ධාරා කොටසක් එලෙස සංඥා ප්රභවය
හරහා යාවි).
ඊට හේතුව
සංඥා ප්රභවයක ඉම්පිඩන්ස්
අගය සාමාන්යයෙන් අඩු අගයක්
වන නිසාය (ධාරාව
හැමතිස්සේම බලන්නේ තමන්ට ගලා
යෑමට අඩුම ප්රතිරෝධය තිබෙන
මාර්ගය කුමක්ද කියානෙ).
CIN
කැපෑසිටරය
හරහා එම ඒසී ෆීඩ්බැක් ධාරාවට
හෙවත් සංඥාවට ගමන් කළ හැකියි.
එහෙත්,
ඩීසී
ෆීඩ්බැක් ධාරාවට එවන් ගැටලුවක්
නැත. ඩීසී
ධාරාවකට කැපෑසිටරයක් හරහා
යෑමට බැහැනෙ.
එනිසා
බයස් එකට බාධා ඇති නොවී සංඥාවට
බාධා ඇති කරයි.
ඇත්තටම
සංඥාව කුමන ආකාරයකින් හෝ
(විශාල
ප්රමාණයකින්)
ෆීඩ්බැක්
වීම කිසිසේත් හොඳ දෙයක් නම්
නොවේ.
මතකද මීට
පෙර RE
මඟින්
සංඥා ෆීඩ්බැක් වීම වැලැක්වීමට
අප බයිපාස් කැපෑසිටරයක්
යෙදුවා.
එනිසා,
මෙතැනදිත්
අපට යම් බයිපාස් කැපෑසිටරයක්
යොදා ගෙන සංඥා ෆීඩ්බැක් වීම
පාලනය කළ යුතු වෙනවා.
ඒ
සඳහා පහත 1
රූපයේ
ආකාරයට බයිපාස් කැපෑසිටරයක්
යෙදීමට එකවර සිතේවි.
එමඟින්
ඔබ සිතනු ඇත්තේ කලෙක්ටරයෙන්
බේසය වෙතට ෆීඩ්බැක් වන සංඥා
කොටස බේසයට යන්නට නොදී කැපෑසිටරය
හරහා කෙලින්ම භූගතයට යවාවි
කියාය;
එමඟින්
නෙගටිව් ෆීඩ්බැක් එක නතර වේවි
කියාය.
එහෙත් ඒ
වෙනුවට ඇත්තෙන්ම සිදු වන්නේ
වෙනත් දෙයකි.
එනම්,
කලෙක්ටරයෙන්
පිට වන සංඥාවෙන් ඉතා විශාල
කොටසක් කෙලින්ම භූගතයට යැවේ;
භාරය හරහා
යෑමට සංඥාවක් ඉතිරි නොවන තරම්ය
(විදුලි
සංඥාව ඉහල ප්රතිරෝධයක් තිබෙන
භාරය හරහා නොගොස් ඉතාම පහල
ප්රතිරෝධයක් දක්වන කැපෑසිටරය
හරහායි ගමන් කරන්නේ).
ඉහත
දෝෂය වැලැක්වීමට නම් බයිපාස්
කැපෑසිටරය ඉහත 2
රූපයේ
ආකාරයට අනෙක් පැත්තෙන් සවි
කිරීම සුදුසු යැයි එවිට ඔබට
සිතේවි.
ඔව්,
එමඟින්
ඉහත ගැටලුව ඉතා හොඳින් විසඳේවි
මොකද දැන් කලෙක්ටරයෙන් පිටවන
සංඥාවට භාරය තුලින් භූගතය
දක්වා හා ෆීඩ්බැක් රෙසිස්ටරය
හරහා කැපෑසිටරය තුලින් භූගතය
දක්වා ලෙස මාර්ග දෙකක් ඇත.
සාමාන්යයෙන්
භාර ප්රතිරෝධයට වඩා ෆීඩ්බැක්
ප්රතිරෝධයේ ඕම් ගණන ඉතා
වැඩිය.
එනිසා,
සංඥාව
භාරය හරහා යාවි;
ෆීඩ්බැක්
රෙසිස්ටරය හරහා එන ඉතා කුඩා
සංඥාවද බේසයට නොගොස් කැපෑසිටරය
හරහා භූගතයට ගොස් ෆීඩ්බැක්
වීම නතර වේ.
එහෙත්
මෙහිදී තවත් අලුත් ගැටලුවක්
මතු වේ.
එනම්,
සංඥා
ප්රභවයේ සිට එන ඉන්පුට් සංඥාව
බේසය හරහා නොගොස් කැපෑසිටරය
හරහා භූගතයට යාවී (ඊට
හේතුව බේස්-එමිටර්
කොටස විසින් ඇති කරන ඉන්පුට්
ඉම්පිඩන්ස් අගයට වඩා බෙහෙවින්
අඩු ප්රතිරෝධයක් කැපෑසිටරය
හරහා පැවතීමයි).
ඉතිං,
ඉන්පුට්
සංඥාව ට්රාන්සිස්ටරයට ඇතුලු
නොවේ නම්,
වර්ධක
පරිපථයෙන් ඇති වැඩකුත් නැත.
එනිසා
බයිපාස් කැපෑසිටරය මෙලෙසත්
යෙදිය නොහැකිය.
ඉහත
ප්රශ්න දෙකටම විසඳුම වන්නේ
බයිපාස් කැපෑසිටරය පහත රූපයේ
ආකාරයට සවි කිරීමයි.
මෙහිදී
ෆීඩ්බැක් රෙසිස්ටර් අගය 2න්
බෙදා බයිපාස් කැපෑසිටරය රූපයේ
ආකාරයට ඒ දෙකට මැදින් සමාන්තරව
සවි කෙරේ.
මෙවිට,
කලෙක්ටරයේ
ඇති සංඥාවට තවමත් භාරයට සාපේක්ෂව
ඉහල ප්රතිරෝධයක් සහිත ෆීඩ්බැක්
ප්රතිරෝධයක් (RF1)
පවතී.
එලෙසම
ට්රාන්සිස්ටරයේ ඉන්පුට්
ඉම්පිඩන්ස් අගයට වඩා වැඩි
ප්රතිරෝධයක් (RF2)
බයිපාස්
කැපෑසිටරයට පෙර පවතී.
ඉතිං,
ඉන්පුට්
සංඥාවෙන් ඉතා විශාලම පංගුව
බේසය තුලට දැන් ඇතුලු වේ.
එලෙසම
අවුට්පුට් සංඥාවෙන් ඉතා විශාලම
පංගුව භාරය හරහා යාවි.
RF1 හරහා
එන කුඩා ෆීඩ්බැක් සංඥා ධාරාවද
බයිපාස් කැපෑසිටරය විසින්
භූගත කෙරේ (මක්නිසාද
යත්, RF1
හරහා
පැමිණි එම ධාරාවට දැන් එතැන්
සිට ඉදිරියට ගමන් කිරීමට ඇති
මාර්ග දෙක වන වැඩි ප්රතිරෝධයක්
සහිත RF2
හා ඉතා
අඩු ප්රතිරෝධයක් තිබෙන
කැපෑසිටරය අතුරින් තෝරා
ගැනෙන්නේ කැපෑසිටරය හරහා
භූගතයට යෑමයි).
එමඟින්
සංඥාව ෆීඩ්බැක් වීම ඇනහිටී.
බයිපාස්
කැපෑසිටරයේ අගය මින් පෙර සෙවූ
ආකාරයටම සොයන්න (මොන
පරිපථයක වුවද බයිපාස් කැපෑසිටරයේ
අගය සොයන ක්රමය වෙනස් නොවේ).
එහෙත්
නෙගටිවී ෆීඩ්බැක් එකේ වාසි
අත්පත් කර ගැනීමට සංඥාවටද
යම් ෆීඩ්බැක් වීමක් සිදු වීමට
ඉඩ දිය හැකිය.
ඒ සඳහා
බයිපාස් කැපෑසිටරය ඉවත් කළ
හැකිය.
ඉහත
රූපයේ දැක්වෙන්නේ කොමන් එමිටර්
වින්යාසයේ පවතින එන්පීඑන්
ට්රාන්සිස්ටරයක් සඳහා
ෆීඩ්බැක් බයස් ක්රමය යොදා
ගෙන සෑදූ ස්මෝල් සිග්නල්
වර්ධකයකි.
උදාහරණයක්
වශයෙන් එහි උපාංගවල අගයන්
තීරණය කරමු.
ෆික්ස්ඩ්
බයස් ක්රමය යටතේ ඉගෙන ගත්
දැනුම මෙහිදී බොහෝ වැදගත්
වේ. එනිසා
මා වැඩි විස්තර රහිතව පරිපථය
නිර්මාණය කරනවා.
සැපයුම්
වෝල්ටියතාව 12
V ලෙස ගමු.
වර්ධකය
ශ්රව්ය සංඛ්යාත පරාසයේ
පවතින සංඥා සඳහා වේ.
ට්රාන්සිස්ටරය
TUN වේ.
එහි β
අගය 150ත්
350ත්
අතර පවතින ලෙස ගමු (සාමාන්ය
අගය 250 ලෙස
ගමු). නිවාත
කලෙක්ටර් ධාරාව දළ වශයෙන් 10
mA ලෙස ගෙන,
කලෙක්ටර්
වෝල්ටියතාව දළ වශයෙන් සැපයුම්
වෝල්ටියතාවෙන් ½
ක් වන සේ
තබමු.
එවිට අපට
සියලු උපාංගවල අගයන් පහත
ආකාරයට ලබා ගත හැකියි.
සටහන
නිවාත
අගයන් බව හැඟවීමට විදුලි
ඒකකවලට Q
යන යටකුර
අවසානයට යෙදිය හැකිය.
එවිට,
ICQ යනු
නිවාත කලෙක්ටර් ධාරාවද,
IBQ යනු
නිවාත බේස් ධාරාවද,
VCQ යනු
නිවාත කලෙක්ටර් වෝල්ටියතාවද,
VCEQ යනු
එමිටරයට සාපේක්ෂව කලෙක්ටර්
නිවාත වෝල්ටියතාවද ආදී වශයෙන්
එම සංඛේතාත්මක ඒකක තේරුම්
ගන්න.
කෙටි
ඒකක/සංඛේත
ඇසුරින් ගණනය කිරීම්වලටත්
හුරු වන්න.
සටහන
KVL
ඉහත
ට්රාන්සිස්ටරයට යෙදීමෙන්ද
ඔබට අවශ්ය සූත්ර ලබා ගත
හැකියි.
ඉන්පුට්
කොටසට කර්චොෆ්ගේ වෝල්ටියතා
නියමය යෙදීමෙන්,
VCC
– ICRC – IBRF – VBE
= 0
VCC
– IERC – (IE/β)RF –
VBE = 0
VCC
– VBE = IE(RF/β + RC)
IE
= [VCC – VBE]/[(RF/β) +
RC]
RF
= β[(VCC – VBE)/IE – RC]
ලෙස
ලබා ගත හැකි අතර,
අවුට්පුට්
කොටසට KVL
යෙදීමෙන්
පහත සූත්රයද ලබා ගත හැකිය.
VCC
– RCIC – VCE = 0
නෙගටිව්
ෆීඩ්බැක් තිබීම නිසා පරිපථය
ස්ථාය වන හැටි බලමු.
අලුත්
ට්රාන්සිස්ටරයක් යෙදීමෙන්
හරි උෂ්ණත්වය විචලනය නිසා
හරි β අගය
වැඩි වන විට,
කලෙක්ටර්/එමිටර්
ධාරාව ඉහල යයි.
එවිට,
කලෙක්ටර්
වෝල්ටියතාව අඩු වී RF
හරහා අඩු
ධාරාවක් බේසයට ඇතුලු වී
පෙරනැඹුරුව අඩු කරයි.
පෙරනැඹුරුව
අඩු වීමෙන් කලෙක්ටර් ධාරාව
අඩු වේ;
β අගය වැඩි
වීමෙන් සිදු වූ වෙනස අහෝසි
වී පරිපථය ස්ථායි වේ.
මීට පෙර
ස්ථායිතාව සොයන ආකාරය ගැන
විස්තර කර තිබෙන බැවින්,
අවශ්ය
නම් මෙම පරිපථයටත් එම ගණනය
කිරීම් සිදු කර බලන්න.
සමහර
අවස්ථාවලදී ට්රාන්සිස්ටරයකින්
සංඥා පිට කිරීමේදී හා
ට්රාන්සිස්ටරයකට සංඥා ඇතුලු
කිරීමේදී ට්රාන්ස්ෆෝර්මර්
භාවිතා වේ (මෙම
කුඩා ට්රාන්ස්ෆෝර්මර්
impedance
matching transformer හෝ
output
transformer ලෙස
හැඳින් වේ);
මේ
ට්රාන්ස්ෆෝර්මර් ගැන පසුවට
ඉගෙන ගනිමු.
ඉතිං,
ෆීඩ්බැක්
බයසිං යෙදූ පරිපථයට සංඥා ඇතුලු
කිරීමට ට්රාන්ස්ෆෝර්මරයක්
භාවිතා කරන්නේ නම් පහත රූපයේ
ආකාරයට පරිපථය සැකසිය හැකිය.
මෙම
වින්යාසයේදී ඉබේම සංඥා
ෆීඩ්බැක් වීම බයිපාස් වීම
සිදු වේ.
මෙලෙස
පරිපථය සකස් කරන විට ඉන්පුට්
කැපෑසිටරයක් යෙදීමට බැරිය.
ඊට හේතුව
ට්රාන්ස්ෆෝර්මරයේ ද්වියිතියික
දඟරය හරහා තමයි බයස්/ඩීසී
විදුලිය සේම සංඥා/ඒසී
විදුලිය යන දෙකම ගමන් කරන්නේ.
ඉතිං,
කැපෑසිටරයක්
එම මාර්ගයේ කොතැනක හෝ යෙදුවොත්
ඩිසී විදුලියට ගමන් කිරීමට
ඉඩක් නැති වී බයස් වීම ඇනහිටී.
අප ඉන්පුට්
කැපෑසිටරය යෙදුවේ ට්රාන්සිස්ටරයේ
බයස් විදුලිය පෙරඅධියරයට
ගමන් කිරීම වැලැක්වීමටනෙ.
ට්රාන්ස්ෆෝර්මරයක
එක් දඟරයකින් අනෙක් දඟරයට
ඩීසී විදුලියක් සංක්රමණය
නොවේ.
එනිසා
කොහොමත් එම කැපෑසිටරය වැඩක්
නැත.
සටහන
ට්රාන්ස්ෆෝමරයද
එක් අතකින් කැපෑසිටරයට යම්
නෑකමක් දක්වයි.
එනම්,
ඒ දෙකම
ක්රියාත්මක වන්නේ ඒසී විදුලිය
සමඟයි.
කැපෑසිටරයක්
හරහා ඩීසී විදුලියක් ගමන්
නොගන්නා සේම,
ට්රාන්ස්ෆෝර්මරයක්
හරහාද ඩීසී විදුලියක් ගමන්
නොකරයි (ඒ
කියන්නේ එක් දඟරයක පවතින ඩීසී
විදුලිය අනෙක් දඟරයට “ගමන්
කරන්නේ” නැත).
කෙසේ
වෙතත් ට්රාන්ස්ෆෝමරයේ පවතින
දඟර දෙකේ වෙන වෙනම ඩීසී විදුලියක්
ගමන් කළ හැකි අතර,
ඒ එක්
දඟරයක පවතින ඩීසී විදුලිය
අනෙක් දඟරයට කිසිදු බලපෑමක්
ඇති නොකරයි.
එහෙත්
එලෙස එක් දඟරයක හෝ දඟර දෙකෙහිම
ඩීසී විදුලියන් තිබීමෙන්
වෙනත් ගැටලු ඇති විය හැකිය
(ට්රාන්ස්ෆෝමර්
කෝර් එක සංතෘප්ත කිරීමෙන්);
විශේෂයෙන්
විශාල ඩීසී ධාරා අගයන් තමයි
ගැටලු ඇති කරන්නේ.
මේ පිළිබඳ
කරුණු මීට පෙර ඉන්ඩක්ටර්
පාඩම්වල අප කතා කර තිබේ.
ඉහත
පරිපථය සටහනේද බේසයට ලබා දෙන
නිවාත/ඩීසී
විදුලිය ද්වියිතියික දඟරයේ
පවතී. එම
ඩීසී විදුලිය ගලා යන ආකාරය
රතු පාටින් දක්වා ඇති අතර,
ඉන්
ප්රාථමික දඟරයට බලපෑමක්
නැත. තවද,
ප්රාථමිකයට
ඇතුලු වන ඉන්පුට් සංඥා විදුලිය
විසින් ද්විතියික දඟරය තුල
සංඥා/ඒසී
විදුලියක්ද ජනනය කරයි;
නිල්
පාටින් එය දක්වා ඇත.
ද්විතියිකය
තුල ප්රේරණය වන සංඥා විදුලිය
ට්රාන්සිස්ටරයේ බේසය තුලට
ගමන් කොට භූගතය හරහා බයිපාස්
කැපෑසිටරය තුලින් නැවත ද්විතියික
දඟරයට ඇතුලු වී පරිපථය සම්පූර්ණ
කර ගනී.
ඒ කියන්නේ
ද්විතියික දඟරය තුලින් විදුලි
වර්ග දෙකක් එකවර මිශ්රව
ට්රාන්සිස්ටරයේ බේසය තුලට
ගමන් කරයි.
තවද,
කලෙක්ටරයේ
සිට ඩීසී ධාරාව සමඟ සංඥා ධාරාවද
එන අතර,
එම ඒසී/සංඥා
විදුලි කොටස බයිපාස් කැපෑසිටරය
විසින් භූගත කර දමයි.
එවිට සංඥා
සඳහා නෙගටිව් ෆීඩ්බැක් එක
නතර වේ.
නිවාත
බයස් ධාරාවට බේසයට ඇතුලු වීමට
පෙර R1,
R2 යන
ශ්රේණිගත රෙසිස්ටර් දෙක
හරහාම යෑමට සිදු වේ.
ඒ කියන්නේ
පෙර අප RF
ලෙස
හඳුනාගත් තනි රෙසිස්ටරයේ අගය
තමයි R1
+ R2 විය
යුත්තේ (රෙසිස්ටර්
දෙකක එකතුවක් ලෙස).
තවද,
R2 යන
රෙසිස්ටරය සංඥා ධාරාව සඳහා
ඉන්පුට් රෙසිස්ටරය (RIN)
ලෙසද
පවතී. ඔබ
දන්නවා RIN
<< RF වන
බව. එනිසා,
කිසිදු
ගැටලුවක් නැතිව R1,
R2 යන
රෙසිස්ටර්වල අගයන් පහසුවෙන්
තීරණය කළ හැකියි.
උදාහරණයක්
ලෙස, RF
= 100k හා RIN
= 10k විය
යුතු යැයි කියා.
එවිට,
අපට හැකියි
R2 =
RIN = 10k ලෙස
සකසා, R1
= RF – RIN = 100k – 10k = 90k ලෙස
තබන්න.
දැන්
ඒසී විශ්ලේෂනයද බලමු.
ධාරා
වර්ධනය (β)
වෙනසක්
නොවේ.
වෝල්ටියතා
වර්ධනය,
ඉන්පුට්
ඉම්පීඩන්ස්,
අවුට්පුට්
ඉම්පිඩන්ස් යන අගයන් සොයා
බලමු.
ස්මෝල්
සිග්නල් වර්ධකවලදී හැමවිටම
වාගේ වෝල්ටියතා වර්ධනය ගැන
පමනක් අවධානය යොමු කරන නිසා,
වැඩි
ප්රමුඛතාවක් ධාරා වර්ධනය
හා ජව වර්ධනය වෙත යොමු නොවේ.
ඉහත
උදාහරණය සලකා,
RIN = 5k නම්,
වෝල්ටියතා
වර්ධනය දළ වශෙයන් -(17.5k/5k)
= -3.5 කි.
ඉන්පුට්
ඉම්පිඩන්ස් අගය සෙවීමට ඇත්තේ
තරමක් විශාල පහත සූත්රයෙනි.
ඉහත
උදාහරණයට ගත් අගයන් ආදේශ කළ
විට, rin
අගය ලෙස
ඕම් 67.5ක්
ලැබේ. මෙම
ඕම් අගයට පිටතින් සවි කර තිබෙන
RIN
අගය එකතු
කර නැත.
ට්රාන්සිස්ටරයේ
ඉන්පුට් ඉම්පිඩන්ස් සමඟ RIN
පවතින්නේ
ශ්රේණිගතව බැවින්,
එම අගයන්
දෙක එකට එකතු කළ යුතු වේ.
එනම් සංඥා
ප්රභවයට ඇත්තටම පෙනෙන
ප්රතිරෝධය වනු ඇත්තේ rin
+ RIN වේ.
තවද,
rin ට
වඩා RIN
ඉතා විශාල
නිසා ඇත්තෙන්ම rin
නොසලකා
හැරිය හැකිය;
ඒ කියන්නේ
ට්රාන්සිස්ටරයේ ඉන්පුට්
ඉම්පිඩන්ස් එක ප්රායෝගිකව
ශූන්ය ලෙස සැලකිය හැකියි.
මෙනිසා
රීතියක්/චාරිත්රයක්
හැටියට සංඥා ප්රභවයේ අභ්යන්තර
ප්රතිරෝධයට සමාන හෝ ඊට වැඩි
අගයක් ලෙස RIN
හි ප්රතිරෝධය
සකස් කරයි.
අවුට්පුට්
ඉම්පිඩන්ස් අගය පහත සූත්රයෙන්
මැනිය හැකිය.
ඉහත
සූත්ර දෙක අධ්යනය කරන විට
පෙනෙනවා ඉන්පුට් ඉම්පිඩන්ස්
සෙවීමට අවුට්පුට් කොටසේ ඇති
කලෙක්ටර් රෙසිස්ටරයත්,
අවුට්පුට්
ඉම්පිඩන්ස් සෙවීමේදී ඉන්පුට්
කොටසේ ඇති rbe
හා RF
රෙසිස්ටර්
අගයනුත් විචල්ය/සාධක
බවට පත්ව තිබෙනවා.
ඒ කියන්නේ
ඉන්පුට් ඉම්පිඩන්ස් අපට අවශ්ය
ප්රමාණයකට සෙට් කරන්නට යන
විට ඉබේම අවුට්පුට් ඉම්පීඩන්ස්
එක වෙනස් වේ;
අනෙක්
අතට අවුට්පුට් ඉම්පිඩන්ස්
අපට අවශ්ය ප්රමාණයට සෙට්
කරන්නට යන විට ඉබේම ඉන්පුට්
ඉම්පිඩන්ස් එක වෙනස් වේ.
මෙය එක්තරා
විදියකින් “උභතෝකෝටිකයකි”.
මෙම බයස්
ක්රමයේ ඇති එක් දෝෂයක් වන්නේද
එයයි.
කොමන්
එමිටර් වින්යාසයේදී සාමාන්යයෙන්
ඉන්පුට් ඉම්පිඩන්ස් අගය කුඩා
වේ. පෙරත්
සඳහන් කළ ආකාරයට ෂන්ට් මික්සිං
ක්රමයට නෙගටිව් ෆීඩ්බැක්
වීම නිසා එම කුඩා ඉන්පුට්
ඉම්පිඩන්ස් එක තවදුරටත් කුඩා
වේ. එයද
මෙම බයස් ක්රමයේ ඇති තවත්
දෝෂයකි.
සටහන
ෆීඩ්බැක්
බයසිං යොදා ගත් කොමන් එමිටර්
වින්යාසයේ පවතින වර්ධකයක්
ට්රාන්ස්රෙසිස්ටන්ස් වර්ධකයක්
ලෙසද සැලකිය හැකිය.
එනම්,
ඉන්පුට්
කරන සංඥාව ධාරාව ප්රමුඛ කර
ගෙනද,
අවුට්පුට්
කරන සංඥාව වෝල්ටියතාව ප්රමුඛ
කර ගෙනද එම වර්ධක පරිපථය
විශ්ලේෂනය කෙරේ.
හැමවිටම
වර්ධකයේ වර්ධන ප්රමාණය තීරණය
කරන්නේ අවුට්පුට් සංඥාව හා
ඉන්පුට් සංඥාව අතර අනුපාතයක්
වශයෙනි.
ඉතිං,
අවුට්පුට්
සංඥාව වෝල්ටියතාවක් නිසාත්,
ඉන්පුට්
සංඥාව ධාරාවක් නිසාත්,
වෝල්ටියතාවක්
ධාරාවකින් බෙදූ විට ලැබෙන්නේ
රෙසිස්ටන්ස්/ප්රතිරෝධයකි.
අවස්ථා
දෙකකට අදාලව මෙම වෝල්ටියතාව
හා ධාරාව පවතින නිසා,
“ට්රාන්ස්”
(හෝ
මියුචුවල්)
යන උපසර්ග
පදයද සහිතව ට්රාන්ස්රෙසිස්ටන්ස්
ලෙස එම ප්රතිරෝධය නම් කෙරෙන
බව මීට පෙර ඔබ ඉගෙන තිබෙනවා.
එනිසා,
මෙම වර්ධකයේ
සත්ය ලෙසම වර්ධන ප්රමාණය
වෝල්ටියතා අනුපාතයක් (AV)
නොව,
ට්රාන්ස්රෙසිස්ටන්ස්
(rT)
විය යුතුය.
දළ
වශයෙන් මෙම වර්ධකයේ
ට්රාන්ස්රෙසිස්ටන්ස් අගය
පහත ආකාරයට වේ.
එනම්,
ෆීඩ්බැක්
රෙසිස්ටරයේ අගය ට්රාන්ස්රෙසිස්ටන්ස්
අගයට සමාන වේ;
ඍන ලකුණින්
කියන්නේ සංඥා අපවර්තනය වන
බවයි.
මොහොතකට
පෙර අප දුටු වෝල්ටියතා වර්ධනය
සොයන සූත්රය පදනම් වන්නේද
මෙම දළ සූත්රය මතයි.
ඉහත
අගය දළ අගයක් වන අතර,
නිවැරදිවම
ට්රාන්ස්රෙසිස්ටන්ස් අගය
සොයන්නට අවශ්ය නම්,
පහත
සූත්රයෙන් එය සෙවිය හැකිය.
ඉහත
ඉතා නිවැරදිව ට්රාන්ස්රෙසිස්ටන්ස්
සොයන සූත්රය යොදා ගෙන එම අගය
සොයා ගත්තේ නම්,
එමඟින්
නිවැරදිව වෝල්ටියතා වර්ධනය
rT
ඇසුරින්
පහත ආකාරයට සෙවිය හැකිය.
මෙහි rin
යනු (β
+ 1)re වේ.
ඉතිං,
ට්රාන්ස්රෙසිස්ටන්ස්
ඈම්ප් එකක් සාමාන්ය වෝල්ටියතා
වර්ධකයක් ලෙසට පරිවර්තනය කර
ගත හැකියි.
ඒ සඳහා
කිරීමට තිබෙන්නේ ඉන්පුට්
සංඥා ධාරාව වෙනුවට ඉන්පුට්
සංඥා වෝල්ටියතාවක් බවට පත්
කර ගැනීමයි.
ධාරාවක්
වෝල්ටියතාවක් බවටත්,
වෝල්ටියතාවක්
ධාරාවක් බවටත් පත් කර ගත හැකි
පහසුතම ක්රමය නම් රෙසිස්ටරයක්
යෙදීම බව මීට පෙර අප ඉගෙන ගත්තා.
ඒ අනුව,
ඉන්පුට්
සංඥා ධාරාව ඉන්පුට් සංඥා
වෝල්ටියතාවක් බවට පත් වීමට
එම ධාරාව රෙසිස්ටරයක් හරහා
යෑමට සලස්වනවා.
පරිපථයේ
ඇති RIN
රෙසිස්ටරය
විසින් තමයි එම රාජකාරියත්
ඉටු කරන්නේ.
ඒ අනුව,
අවසාන
වශයෙන් ගත් කළ,
එම සමස්ථ
පරිපථයම වෝල්ටියතා වර්ධකයකි.
RIN යෙදීමේ
වැදගත්කම නැවතත් මතු වේ.
මෙම
බයස් ක්රමය තවත් ස්ථාවර
කිරීමට එමිටර් රෙසිස්ටරයක්ද
යෙදිය හැකිය.
RE යෙදීම
ගැන දිගු විස්තරයක් මීට පෙර
සිදු කර ඇත.
එනිසා,
KVL යොදා
ඔබටම මෙම පරිපථය සඳහා අවශ්ය
සම්බන්ධතා ගොඩනඟා ගත හැකිය.
අභ්යාසයක්
ලෙස එය සිදු කර බලන්න.






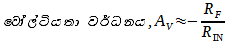
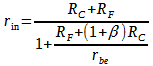





Comments
Post a Comment
Thanks for the comment made on blog.tekcroach.top