ඇල්ෆා
කෝණය, කේ
අගය, තරංග
ආයාමය අතර සම්බන්දතාවක්
ගොඩනැඟිය හැකිය.
මෙවිට
එම පරාමිතින් 3
නිසි ලෙස
සීරුමාරු කර තමන්ට අවශ්ය
ගතිගුණ තිබෙන ඇන්ටනාවක්
නිර්මාණය කර ගත හැකි වෙනවා.
එම සම්බන්දතාව
ගොඩනැඟීමට ඉහත ඇන්ටනාව ඇසුරින්ම
සකස් කර ගත් පහත රූප සටහන බලන්න.
දැන්
අපට පහත ආකාරයට සූත්රයක්
සාදා ගත හැකියි.
මෙහි Sλ
යනු S/λ
වේ.
එනම් කූරු
අතර පරතරය තරංග ආයාමය ඇසුරින්
දක්වනවා.
මෙම Sλ
අගය සුදුසු
අගයක තිබිය යුතුය.
දළ වශයෙන්
එම අගය 0.258τ
– 0.066 යන
සූත්රයට අනුව ලැබෙන අගයට
තැබීමට උත්සහ කළ යුතුය (මෙම
අගය ඇන්ටනාවෙන් උපරිම ගේන්
එක ලැබෙන අවස්ථාවයි).
එය 0.05
ට වඩා අඩු
වුවොත් බැක්ලෝබ් එක විශාල
වන්නට පටන් ගනී.
එලෙසම,
එම අගය
ඉහත සූත්රයෙන් ලැබෙන අගයට
වඩා වැඩි වුවොත්,
සයිඩ්ලෝබ්
වැඩි වේවි.
ඉහත
සාධක/පරාමිතින්
3 අතර
සම්බන්දතා අගයන් ලෙස ගෙන සකසා
ගත් ප්රස්ථාරයක් පහත දැක්වේ.
එහි
දැක්වෙනවා ඉහත අගයන් 3
විචලනය
කරන විට,
ඇන්ටනාවේ
ගේන් එක වෙනස් වන හැටිත්.
සාමාන්යයෙන්
කේ අගය 1.25
ට වැඩිය
ගැනීම සුදුසු නැත (එනිසා
ප්රස්ථාරයේ එම අගයෙන් පසුව
වැඩක් නැත).
කේ අගය
අඩු වන තරමට ගේන් එක වැඩි වන
බව පෙනේ.
මෙම
ප්රස්ථාරය උපයෝගි කර ගෙන
දැන් හැකියි අපට අවශ්ය ගතිගුණ
තිබෙන ඇන්ටනාව නිර්මාණය කර
ගන්නට.
උදාහරණයක්
ලෙස, කේ
අගය 1.25 ද,
ඇල්ෆා
කෝණය අංශක 19ද,
Sλ අගය
0.14 පමණ
වන විට,
ගේන් එක
6.6dBi කි.
පහත රූපයේ
රතුපාට ඉරිවලින් දක්වා තිබෙන්නේ
මෙම උදාහරණයයි.
මීට
පෙර ඉගෙන ගත් ln+1/l1
= kn = බෑන්ඩ්විත්
අනුපාතය (F)
යන සූත්රය
මතකද?
K=1.25 හා n=4
නම් (එනම්
කූරු 5ක
ඇන්ටනාවක්),
සංඛ්යාත
අනුපාතය වන්නේ k4
= 1.254 = 2.44 වේ.
ඒ කියන්නේ
ඇන්ටනාවේ පොඩිම ඩයිපෝල් කූරට
වඩා 2.44
ගුණයක්
විශාලයි ඇන්ටනාවේ දිගම ඩයිපෝල්
කූර. එම
අනුපාතයම තිබෙනවා බෑන්ඩ්විත්
එකටත්.
උදාහරණයක්
ලෙස, ලොකුම
කූරෙන් මෙගාහර්ට්ස් 100
සපෝට්
කරයි නම්,
ඇන්ටනාව
විසින් මෙගාහර්ට්ස් 100x2.44
= 244 දක්වාම
සපෝට් කරාවි.
ඉහත
සියලු විස්තර සැලකිල්ලට ගෙන
ඇන්ටනාවක් දැන් නිර්මාණය කරන
හැටි බලමු.
7dBi ක
ඇන්ටනාවක් බෑන්ඩ්විත් අනුපාත
අගය 5ක්
(5 to 1) සහිතව
නිර්මාණය කිරීමට අවශ්ය යැයි
සිතමු.
මෙවිට
අවශ්ය ඇල්ෆා කෝණය,
කේ අගය,
හා ඉලෙමන්ට්
ගණන ගණනය කරන්න.
මෙහිදී
ඉතාම නිවැරදිම අගයන් අත්යවශ්ය
නැත. දළ
අගයන් යොදා ගත හැකිය.
ඉහත
ප්රස්ථාරය අනුව,
7dBi අගයේදී
කෝණය අංශක 15ක්
පමන වේ.
එවිට කේ
අගය 1.2 පමන
වේ. F=kn
නිසා,
5=1.2n වේ.
එය සුලු
කළ විට,
n=8.82 වේ.
n අගය දශම
ගණනක් විය නොහැකියිනෙ.
හැමවිටම
ලැබෙන අගය ආසන්නතම ඉහල පූර්ණ
සංඛ්යාව ගන්න.
එවිට n=9
ලෙස ගත
හැකියි.
ඊට තවත්
1ක්
එකතු කරන්න.
ඒ කියන්නේ
ගණනය කිරීම්වලින් කූරු 10ක්
අවශ්ය බව ලැබුණි.
වැඩි හොඳට
අවශ්ය නම් තවත් කූරක් හෝ
දෙකක් එකතු කළ හැකියි.
අපි වැඩිපුර
තවත් කූරක් දමමු;
එවිට
ඇන්ටනාවේ කූරු 11ක්
තිබිය යුතුය.
මෙම
ඇන්ටනාව ඩයිපෝල ගණනාවක එකතුවක්
ලෙස සැලකිය හැකියිනෙ.
ඉන් එක්
ඩයිපෝලයක් තනිව ගත් විට,
එහි සම්බාදක
අගය Zan
= 120[ln(ln/dn)
– 2.25] යන
සූත්රයෙන් ලැබේ.
එහි ln
යනු යම්
(n වැනි)
ඩයිපෝල්
කූරේ දිග වන අතර,
dn යනු
එම කූරේ විශ්කමභ අගයයි.
මෙම සූත්රය
අනුව,
ඇන්ටනාවේ
තිබෙන සෑම ඩයිපෝලයකටම එකම
සම්බාදක අගයක් පැවතීමට ln/dn
අනුපාතය
එක සමාන විය යුතුය.
ඒ කියන්නේ
කූරේ දිග වෙනස් වන විට ඊට
අනුරූපව කූරේ විශ්කම්භයද
වෙනස් විය යුතුය.
එහෙත්
ප්රායෝගිකව එය කළ නොහැකිය
(එනම්
එක් එක් කූර අපට අවශ්ය අවශ්ය
විශ්කම්භ අගයන්ගෙන් ලබා ගත
නොහැකිය).
තවද,
ඇන්ටනාවේ
දැන් තිබෙන්නේ තනි ඩයිපෝලයක්
නොව ඩයිපෝල් සෙට් එකකි.
එනිසා
ඉහත සූත්රයෙන් ලැබෙන සම්බාදක
අගයට වඩා වෙනස් අගයකුයි
තිබෙන්නේ.
එම අගය
දළ වශයෙන් පහත සූත්රයෙන්
සෙවිය හැකිය.
මෙහි R0
යනු සමස්ථ
ඇන්ටනාවේ සම්බාදක අගයයි.
Z0 යනු
ෆීඩ්ලයින් එකේ කැරක්ටරිස්ටික්
ඉම්පීඩන්ස් එකයි.
Za යනු
එක් ඩයිපෝල් කූරක සම්බාදක
අගයයි (මීට
පෙර ඡේදයේ විස්තර කළ ලෙස සෑම
කූරකම සම්බාදක අගය සමාන යැයි
උපකල්පනය කරමු).
τ = 1/k වේ.
σ යනු
(Rn+1
– Rn)/2ln+1
යන අගයයි
(එම
සිග්මා අගය spacing
factor ලෙස
හැඳින්වේ).
පහත සූත්රය
අනුව පැහැදිලියි ඇන්ටනාවේ
ඉම්පීඩන්ස් අගය k
(τ) අගය
මත විචලනය වන බව.
දැන්
මෙම ඇන්ටනාව එක්කෝ මුලින්ම
පෙන්වා දුන් ආකාරයට සෑදිය
හැකියි.
එවිට
සාමාන්ය කොඇක්සියල් (ඕම්
50 හෝ
75) කේබලයක්
ෆීඩ්ලයින් එක ලෙස භාවිතා කළ
හැකියි.
කොඇක්ස්
කේබලයේ මැද කම්බිය උඩ බූම්
එකටත්,
බ්රෙයිඩ්
එක යට බූම් එකටත් සම්බන්ද
කරන්න.
එසේත්
නැතිනම්,
මෙම ඇන්ටනාව
දෙවනුව පෙන්වා දුන් dipole
array එකක්
ලෙස සැකසිය හැකියි.
මෙවිට
එය ඕම් 300
ක බැලැන්ස්ඩ්
කේබලයක් ෆීඩ්ලයින් එක ලෙස
භාවිතා කරන්න.
සමහරවිට
බූම් දෙකට ෆීඩ්ලයින් එක සම්බන්ද
කරන්නට සිදු වන්නේ ඇන්ටනා
බම්බුව ළඟ තිබෙන කෙළවරට නොව
අනෙක් කෙලවරටයි.
මෙවිට
ඇන්ටනාවේ යට බූම් එකේ යට
පැත්තෙන් එම කේබලය ඉදිරියට
ගෙන යා හැකිය පහත රූපවල පෙන්වා
ඇති ලෙස.
ෆීඩ්පොයින්ට්
එකේදී ෆීඩර් හෙවත් බූම් අතර
පරතරය හා ෆීඩර්හි විශ්කම්භය
අතරද පැවතිය යුතු සුදුසු
සම්බන්දතාවක් තිබේ.
තිරස්
හෝ සිරස්ව තැබීමෙන් ලීනියර්
පොලරයිසේෂන් එක වෙනස් කර ගත
හැකිය.
තවද,
ගිගාහර්ට්ස්
කලාපය සඳහා ඉතා කුඩාවට සාදා
ගත හැකියි.
පරිපථ
සෑදීමට ගන්නා PCB
බෝඩ් මතද
පහසුවෙන්ම මෙවන් ඇන්ටනාවක්
සෑදිය හැකිය (පහත
රූපයේ කොලපාටින් පෙන්වන්නේ
එලෙස සාදා ගත් ඉතා කුඩා අඩුජව
භාවිතා සඳහා යොදා ගත හැකි
ඇන්ටනාවකි).
අවශ්ය
නම් භාහිර ආවරණයක් තුල ඇන්ටනාව
බැස්සවිය හැකිය.
මෙම
ඇන්ටනාව සාදන තවත් ක්රමයක්
පහත ඇත.
එහිදී
ඉහත ඇන්ටනාවේ එක උඩ එක තැබූ
බූම් දෙක පහත රූපයේ ආකාරයට
කෝණයක් සහිතව තබයි.
පහත රූපයේ
ඇති අගයන් යම් උදාහරණයට ගත්
ඇන්ටනාවක් සඳහා වලංගු වේ.
බලන්න
බූම් දෙක යම් කෝණයක් සෑදෙන
පරිදි ඈත් කර ඇත.
ඇන්ටනාවේ
අනෙක් අගයන් මීට පෙර උගත්
ක්රමයටයි සකසා ගෙන තිබෙන්නේ.
උඩ බූම්
එක ගත් විට,
ඊට සවි
කරන කූරු මාරුවෙන් මාරුවට
දෙපැත්තටයි සවි කරන්නේ සුපුරුදු
ලෙසම. ඊට
පහලින් ඇති බූම් එකෙත් එලෙසමයි.
ඉහත
ආකාරයට සාදා ගත් ඇන්ටනාව පහත
ආකාරයට පෙනේවි.
මෙවැනි
කෝණයක් සහිතව සාදන ඇන්ටනාවකදී
ෆීඩ්පොයින්ට් එක තැබිය යුත්තේ
ඉහත රූපයේ පෙන්වා තිබෙන ලෙසට
බූම්/දඬු
දෙක ළං වන ස්ථානයේය.
සාමාන්යයෙන්
කොඇක්සියල් කේබලයක් භාවිතා
කරන විට,
එහි සිග්නල්
පාත් එක උඩ දණ්ඩටත්,
රිටර්න්
පාත් එක යට දණ්ඩටත් සවි කෙරේ.
මෙම
ඇන්ටනාවේ ගේන් එකට ඇන්ටනා
කූරුවල විශ්කම්බය එතරම් බල
පාන්නේ නැත (එහෙත්
කූරේ ඝනකම වෙනස් කරන විට එම
ඩයිපෝල් කූරේ සම්බාදක අගය
නම් වෙනස් වේ).
කූරේ ඝනකම
දෙගුණයක් කරන විට ගේන් එක
0.2dB වැනි
කුඩා ප්රමාණයකිනුයි වැඩි
වන්නේ.
එහෙත්
ඇන්ටනාවේ ගේන් එක වැඩි කර
ගැනීමට ලොග් පීරියඩික් ඇන්ටනා
දෙකක් පහත රූපයේ ආකාරයට තැබිය
හැකිය (stacked
antenna). මෙවිට
සාමාන්යයෙන් එම ඇන්ටනා දෙක
තබන කෝණ අගය අංශක 60ක්
පමණ වේ.
ඉහත
ආකාරයට නිම කර ගත් ඇන්ටනාවක්
පහත දැක්වේ.
මෙලෙස
ස්ටැක් කරන ඇන්ටනා දෙක සාමාන්ය
ලොග් පීරියඩික් හෝ ඩයිපෝල්
ඇරේ හෝ මොහොතකට පෙර පෙන්වා
දුන් කෝණිකව සකස් කළ බූම් සහිත
ආකාරය ආදී ඕනෑම ආකාරයකින්
තිබිය හැකිය.
පහත රූපයේ
ඇත්තේ කෝණිකව සකස් කළ බූම්
සහිත ඇන්ටනා දෙකක් ස්ටැක් කර
තිබෙන ආකාරයයි.
මෙම ඇන්ටනාව
කේසිං එකක් තුල දැමූ විට පෙනෙන
ආකාරයත් එහි කුඩා රූපයෙන්
දැක්වේ.
මීටත්
අමතරව තවත් විවිධාකාරයෙන්
මෙම ලොග් පීරියඩික් ඇන්ටනා
සකස් කළ හැකිය.
උදාහරණයක්
ලෙස, පහත
දැක්වෙන ලෙසට සිරස් හා තිරස්
යන දිශා දෙක ඔස්සේම කූරු සහිතව
සෑදූ විට සිරස් හා තිරස්
පොලරයිසේෂන් දෙකෙන්ම යුතු
රේඩියෝ විකිරණය සම්ප්රේෂනය/ග්රහනය
කරයි.
මෙහිදී
එකිනෙකට ලම්භකව තිබෙන කූරු
එකිනෙකාට බලපෑම් කිරීම ඉතාම
අල්පය (එනිසා
වෙන වෙනම සාමාන්ය ලොග්
පීරියඩික් ඇන්ටනා දෙකක් ලෙස
වෙන වෙනම ඉහත සඳහන් කළ විස්තරවලට
අනුව ඒවා සාදා ගත හැකිය).
මෙහිදී
ලම්භක ඇන්ටනා දෙකට වෙන වෙනම
සංඥා දෙකක් ඇතුලු කළ යුතුය.
එය පහත
රූපයේ ආකාරයට කළ හැකියි.
මෙවිට
ඇන්ටනාවට සම්බන්ද කරන ෆීඩ්ලයින්
එකේ සම්බාදක අගය අවම වශයෙන්
ඕම් 106ක්
වත් විය යුතුය.



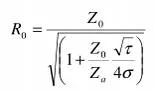










Comments
Post a Comment
Thanks for the comment made on blog.tekcroach.top