quaternion
(ක්වෝටර්නියන්)
ගැනයි අප කතා
කරන්නට යන්නේ. එය
ගණිත සංකල්පයකි. ඇත්තටම
මාද මේ ගැන ගැඹුරු හැදෑරීමක් කර නැත; මාගේ අධ්යන කටයුතුවලදී ක්වෝටර්නියන් හමු නොවීම ඊට
හේතුවයි. ජීවිතේට
මේ ගැන ලිවීමට සිතා නොසිටියත් එකවරම මෙම කුඩා ලිපිය ලියන්නට හේතුව වූයේ ඊයේ රාත්රියේ
මගේ බ්ලොගයේ තිබූ කමෙන්ටුවකි (https://www.tekcroach.tk/2017/12/amateur-radio-121.html?showComment=1516351179602#c5339757654033845008).
එම කමෙන්ටුව
දැකීමෙන් පසු අන්තර්ජාලයේ ඒ සම්බන්දයෙන් සිංහල බසින් කිසිත් ලියා ඇත්දැයි "ක්වෝටර්නියන්"
යන වචනය ගූගල්
කළ විට (සුපුරුදු
ලෙසම) එකදු
ලිපියක්වත් හමු නොවීය. ඉන්පසු
සමහරවිට ක්වෝටර්නියන් යන්නට සමාන සිංහල පාරිභාෂික වචනයකින් ඒ ගැන ලියා ඇත්දැයි
සෙවීමට ක්වෝටර්නියන් යන්නෙහි සිංහල පාරිභාෂික වචනය වන "චතුෂ්ටය " ඔස්සේද ගූගල් කළ විටද
මෙම ගණිත සංකල්පය ගැන එකදු ලිපියක්වත් අන්තර්ජාලය තුල නොවීය. අපේ විජ්ජවිජ්ජාල (ඒවායේ විද්යා/දර්ශන පීඨ ගැන
විශේෂයෙන්) හා
ඒවායේ සිටිනවා යැයි කියන ගුරු හා ශිෂ්ය "විද්යාර්ථින්" ගැන ලොකු ආඩම්බරයක්ද
දැනෙනවා ඇත්තෙන්ම!
පොඩි එකෙකු පවා 2,
-64, 814782, 573.63 ආදි
සංඛ්යා ගැන දන්නවානෙ. මේවා
තාත්වික සංඛ්යා (real numbers) ලෙස ගණිතය තුල හඳුන්වමු. තවදුරටත් ගොස් කැමති
නම් පහත රූපයේ ආකාරයට ඕනෑම තාත්වික සංඛ්යාවක් තිරස් රේඛාවක (මෙය තාත්වික රේඛාව
- real number line නමි)
නිරූපණයද කළ
හැකිය. තාත්වික
සංඛ්යා දෙකක් එකතු කළ විට, අඩු
කළ විට, වැඩි
කළ විට, බෙදූ
විට, බලයකට
නැංවූ විට ආදී ලෙස ගණිත කර්ම සිදු කළ පසුත් අපට ලැබෙන්නේ තාත්වික සංඛ්යාවක්මයි (ගණිතය තුල මෙවන්
ගතිගුණයක් closure property ලෙස හැඳින්වේ).
එහෙත් යම් තාත්වික
සංඛ්යාවක වර්ගමූලය ගත් විට හැමවිටම තාත්වික සංඛ්යාවක්ම ලැබෙන්නේ නැත. 4 හි වර්ගමූලය ධන හෝ ඍන
2 වේ;
1 හි වර්ගමූලය
ධන හෝ ඍන 1 වේ.
එම අවස්ථාවල
තාත්වික සංඛ්යා ලැබුණත්, -4 හෝ
-1 හෝ (වෙනත් ඕනෑම ඍන සංඛ්යාවක)
වර්ගමූලය (හෝ ඉරට්ටේ මූලයක්)
ගත් විට එලෙස
අපට තාත්වික සංඛ්යාවක් ලබා ගත නොහැකිය. මෙනිසා, අතාත්වික සංඛ්යා (imaginary
numbers) යන
සංකල්පය හඳුන්වාදුනි. අතාත්වික
සංඛ්යා පදනම්ව ඇත්තේ හෙවත් නිර්වචනය කර ඇත්තේ √-1 = i (හෙවත් i2 = -1) යන සම්මුතිය අනුවය. ඒ අනුව, ඍන
සංඛ්යාවක වර්ගමූලය දැන් අපට නිරූපනය කළ හැකියි.
√-1 = i
√(-4) = √(4 x -1) = √4 x √-1 = √4
i = ±2i
√-7.2 = √7.2i
මේ අනුව, සෑම අතාත්වික සංඛ්යාවක්ම i සහිතයි. දැන්
අපට හැකියි තාත්වික සංඛ්යා දෙකක් මත ගණිත කර්ම සිදු කළ ආකාරයටම, අතාත්වික සංඛ්යා 2ක් මතත් එකතු කිරීම, අඩු කිරීම, වැඩි කිරීම, බෙදීම ආදි ගණිත කර්ම සිදු කරන්නට.
3i + 2i = 5i
-5i + 4i = -1i = -i
6i - 3i = 3i
2i x 4i = 8i2 = 8 x
-1 = -8
8i / 2i = 4
(2i)4 = 2i x 2i x 2i
x 2i =16 x i4 = 16 x i2 x i2 = 16 x -1 x -1 =
16
(2i)3 = 2i x 2i x 2i
= 8i3 = 8 x i2 x i = 8 x (-1) x i = -8i
ඉහත ගණනය
කිරීම්වලින් පෙනෙනවා අතාත්වික සංඛ්යා දෙකක් වැඩි කිරීම හා බෙදීම නිසා අපට
ලැබෙන්නේ තාත්වික සංඛ්යා බව (එනම් ක්ලෝසර් ප්රොපර්ටි/ලක්ෂනය අතාත්වික සංඛ්යා ගුන කිරීමේදී
හා බෙදීමේදි නැත). අතාත්වික සංඛ්යා
බලයකට නැංවීමේදී සමහර අවස්ථාවලදී (එනම් දර්ශකය ඔත්තේ
වන විට) අතාත්වික සංඛ්යාත්
තවත් සමහර අවස්ථාවකදී (එනම් දර්ශකය ඉරට්ටේ
වන විට) තාත්වික සංඛ්යාත්
ලැබෙන බව පෙනේ. අපට හැකියි අතාත්වික
සංඛ්යාත් ඍන අනන්තයේ සිට ධන අනන්තය දක්වා පහත ආකාරයට ජ්යාමිතිකව නිරූපණය කරන්නට "සිරස්" රේඛාවක් මඟින්. මෙය අතාත්වික සංඛ්යා රේඛාව (imaginary number line) වේ.
තාත්වික හා
අතාත්වික සංඛ්යා/අගයන් දෙකක්
එකිනෙකට එකතු (හෝ අඩු) කළ විට ලැබෙන සංඛ්යාවට අප සංකීර්ණ
සංඛ්යාවක් (complex
number) යැයි කියනවා. උදාහරණයක් ලෙස, 5 යන තාත්වික සංඛ්යාව 2i යන අතාත්වික සංඛ්යාව සමඟ එකතු කළ විට, එය පහත ආකාරයට නිරූපණය කෙරෙනවා. තෙල් හා ජලය එකිනෙකට මිශ්ර කළාට මිශ්ර
නොවී වෙන වෙනම ස්ථර දෙකක් ලෙස පවතින්නාක් සේ,
තාත්වික
හා අතාත්වික යනු එකිනෙකට නොගැලපෙන සංඛ්යා දෙකක් නිසා, පහත ආකාරයට එම සංඛ්යා කොටස් දෙක වෙන
වෙනම + ලකුණ දෙපස දැක්වීමට
සිදු වෙනවා.
5 + 2i
එනිසා ඕනෑම සංකීර්ණ
සංඛ්යාවක් පොදුවේ ලියන්නේ a
+ bi යන ක්රමයටයි. මෙහි a යනු
තාත්වික කොටස (real
part) හා b යනු අතාත්වික කොටස (imaginary part) ලෙස හැඳින්වේ. මේ නිරූපණය ක්රමය හැරෙන්නට ඇත්තටම
සංකීර්ණ සංඛ්යාවක් නිරූපණය කළ හැකි තවත් ක්රම 2ක්
තිබෙනවා - r(cosθ +
isinθ) යන
ධ්රැවීය නිරූපණය හා reiθ
යන
ඔයිලර් නිරූපණය. ඇත්තටම, සංකීර්ණ සංඛ්යා යනු තාත්වික හා
අතාත්වික සංඛ්යා යන දෙකෙහිම පොදු ආකාරයයි.
ඒ
කියන්නේ සංකීර්ණ සංඛ්යාවක් මඟින් (එනම් එම නිරූපණ ක්රමය
මඟින්) අපට හැකියි තාත්වික
සංඛ්යාවක් හෝ අතාත්වික සංඛ්යාවක් නිරූපණය කරන්නට.
0 + 4i = 4i (මෙය අතාත්වික සංඛ්යාවකි)
5 + 0i = 5 (මෙය තාත්වික සංඛ්යාවකි)
දැන් අපට හැකියි
එකිනෙකට ලම්භක තාත්වික සංඛ්යා රේඛාව හා අතාත්වික සංඛ්යා රේඛාව එකට ඇඳ කාටිසියානු
තලයකට සමාන ආකාරයක් ලබා ගෙන,
ඒ
මත ඕනෑම සංකීර්ණ සංඛ්යාවක් නිරූපණය කිරීමට (එවිට, ඉබේම තාත්වික සංඛ්යාද, අතාත්වික සංඛ්යාද නිරූපණය කළ හැකිය). මෙවිට, තිරස්
අක්ෂය තාත්වික අක්ෂය (real
axis) ලෙසද, සිරස් අක්ෂය අතාත්වික අක්ෂය (imaginary axis) ලෙසද, සමස්ථ
ප්රස්ථාරයම ආගන්ඩ් තලය (Argand
plane) හෙවත් සංකීර්ණ තලය (complex
plane) ලෙසද නම් කරනු
ලබනවා.
මෙම ලිපියේ මූලික
අරමුණ ක්වෝටර්නියන් ගැන කතා කිරීමට බැවින් හා සංකීර්ණ සංඛ්යා ගැන මා වෙනම
විස්තරාත්මකව ලිපි පෙලක්ම ලියා ඇති බැවින් සංකීර්ණ සංඛ්යා ගැන මෙතැනින් නවතනවා. තාත්වික සංඛ්යා, අතාත්වික සංඛ්යා, හා සංකීර්ණ සංඛ්යා ගැන කෙටියෙන් හෝ ප්රථමයෙන්
විස්තර කළේ ක්වෝටර්නියන් යනු සංකීර්ණ සංඛ්යා සංකල්පයේ විස්තීර්ණ අවස්ථාවක්
බැවිනි. දැන් ඒ ගැන බලමු.
සංකීර්ණ සංඛ්යාවට
පදනම වූයේ √-1 = i යන සම්මුතියයි (සම්මුතියක් යනු "අපි මෙහෙම යැයි සිතමු" යැයි කවුරුත් ඒකමතිකව ගත් තීරණයකි). එලෙසම දැන් අපට හැකියි ක්වෝටර්නියන්
සංඛ්යාවක් ("ක්වෝටර්නියන් සංඛ්යාව" යන්න වෙනුවට නිකංම "ක්වෝටර්නියන්" යැයි ව්යවහාර කෙරේ) පහත ආකාරයට සම්මුතික වශයෙන් අර්ථ
දක්වන්නට. ඇත්තටම මෙම අර්ථ
දැක්වීම මෙසේ විය යුතු යැයි 1843
දී
පමණ පළමු වරට යෝජනා කරමින් ක්වෝටර්නියන් සංකල්පය හෙවත් ක්වෝටර්නියන් සංඛ්යා
පද්ධතිය හඳුන්වා දුන්නේ විශිෂ්ට ගණිතඥයකු වන විලියම් රෝවන් හැමිල්ටන්
විසිනි. සාමාන්යයෙන්
තාත්වික සංඛ්යා R මඟින්ද, සංකීර්ණ
සංඛ්යා C මඟින්ද, ක්වෝටර්නියන්
H මඟින්ද ගණිතයෙදී සංඛේතවත් කෙරේ. මෙහි a යන
කොටස අදිශ කොටස (scalar
part) ලෙසද, bi + cj + dk යන
කොටස දෛශික කොටස (vector
part) ලෙසද
හැඳින් වෙනවා.
H = a + bi + cj + dk
බැලූබැල්මටම
ක්වෝටර්නියන් හා සංකීර්ණ සංඛ්යාවක් අතර සමීපබවක් පේනවා නේද? ඔව්; ක්වෝටර්නියන්
එකක අතාත්වික කොටස් 1ක් නොව 3ක්ම තිබෙනවා. අවශ්ය නම් ඒවා i1, i2, i3
ලෙස
නිරූපණය කළ හැකි වුවත්,
වඩා
පහසුවෙන් ඒවා හැසිර වීමට i,
j, k ලෙස ලියා දක්වනවා. මෙහි, a, b, c, d යන කොටස් ඇත්තටම වීජීය ප්රකාශයක
සංගුණක (coefficient)
බඳුය; ඒවා තාත්වික අගයන්ය. i, j, k තුන quaternion units (ක්වෝටර්නියන් ඒකක) ලෙස හැඳින්වේ.
ක්වෝටර්නියන් එකක්
මඟින් අවශ්ය නම් තාත්වික සංඛ්යාවක්,
අතාත්වික
සංඛ්යාවක්, සංකීර්ණ සංඛ්යාවක්
වුවත් නිරූපණය කළ හැකිය.
ඒ
කියන්නේ සංකීර්ණ සංඛ්යාවම තවත් වැඩිදියුණු කිරීමක් (විස්තීර්ණ කිරීමක්) ලෙස එය
සැලකිය හැකියි.
4 + 0i + 0j + 0k = 4 (මෙය සාමාන්ය
තාත්වික සංඛ්යාවක් නේද?)
0 + 2i + 0j + 0k = 2i (මෙය සාමාන්ය
අතාත්වික සංඛ්යාවකි)
5 + 4i + 0j + 0k = 5 + 4i (මෙය සාමාන්ය
සංකීර්ණ සංඛ්යාවකි)
ඇත්තටම, ඉහත උදාහරණ 3න් දෙවැනි එකට අනුරූප තවත් අවස්ථා 2ක් ඇත. එනම්, 0 + 0i + 2j + 0k හෙවත් 2j හා 0 + 0i + 0j + 2k හෙවත් 2k යනුද
2i අවස්ථාවටම අනුරූප
අවස්ථා වන අතර, ඒවාද අතාත්වික සංඛ්යා
ලෙස සැලකිය යුතුය. තවද, 2i + j, 4i
+ 5k, 7j + k, 8i + j + 2k ආදි ලෙස අතාත්වික කොටස් දෙකක හෝ තුනෙහිම “මිශ්රණවලටත්”
අතාත්වික යැයි කියනවා. සාමාන්ය
අතාත්වික සංඛ්යාවකින් (4i
වැනි) මෙලෙස ක්වෝටර්නියන් ඇසුරින් නිරූපණය
කෙරෙන අතාත්වික සංඛ්යා විශේෂ කොට හැඳින්වීමට 4i, 4k, 4j, 2i + j, 4i
+ 5k, 7j + k, 8i + j + 2k ආදි අතාත්වික සංඛ්යා "ශුද්ධ අතාත්වික" (pure imaginary) යැයි හඳුන්වනවා.
ඇත්තටම H
= a + bi + cj + dk යන්න ක්වෝටර්නියන් එකක් බවට සැලකීම සිදු වන්නේ
පහත සඳහන් අනිවාර්ය පූර්ව කොන්දේසිය යටතේය (මෙම කොන්දේසිය හැමිල්ටන් විසින්ම පනවන
ලද්දකි).
i2 = j2 = k2 =
ijk = -1
i2 = -1 යන්න
සංකීර්ණ සංඛ්යාවලත් සම්මතයනෙ. එම සම්මතයම තවදුරටත් ඉදිරියට ගෙනයමින් ඉහත ආකාරයට
කොන්දේසියක්/සම්මතයක් ඇති කළේය. මෙහි අවසානයට ඇති ijk යන ගුණිතයත් -1 ට සමාන කිරීම නිසා ක්වෝටර්නියන්වල
අපූරු ගතිගුණ ලැබේ. දැන් ඒ ගැන බලමු. එනම්, පහත දැක්වෙන ගතිගුණද පවතී.
i x j = k
j x k = i
k x i = j
j x k = i
k x i = j
ඉහත සම්බන්දතා පවතින බව පහත සාධනය මඟින් ඔප්පු වේ.
ijk = (ij)k = (k)k = kk = k2 = -1 හෝ
ijk = i(jk) = i(i) = i2 = -1 හෝ
ijk = i)j(k = j(j) = j2 = -1
තවද, ක්වෝටර්නියන් දෙකක් අතර තිබෙන ගුණිතය න්යාදේශ්ය නියමය (commutative law) පිළිපදින්නේ
නැත. එනම් H1
x H2 ගුණ කළ විට ලැබෙන පිළිතුර නොවෙයි H2 x H1 ලෙස පද මාරු කරගෙන ගුණ කළ විට ලැබෙන්නේ. ඒ වෙනුවට (H1 x H2) = - (H2 x H1) ලෙස පවතී. විශේෂයෙන් එය මතක තබා ගත යුතුමය. මෙම
ගතිගුණය නිසා, පහත ආකාරයට සම්බන්දතා ඇති වේ.
j x i = -k (එනම්, j x i = -(i
x j) වේ)
k x j = -i (එනම්, k x j = -(j x k) වේ)
i x k = -j (එනම්, i x k = -(k x i) වේ)
k x j = -i (එනම්, k x j = -(j x k) වේ)
i x k = -j (එනම්, i x k = -(k x i) වේ)
ක්වෝටර්නියන් එකක් රූපමය ආකාරයෙන්ද නිරූපණය කළ හැකියි. සාමාන්යයෙන්
මිනිසා ත්රිමාන අවකාශය සංජානනය කරන බැවින් ක්වෝටර්නියන් එකක කොටස් 4ක් තිබෙන
බැවින් එකිනෙකට ලම්භකව අක්ෂ 4ක් අපට ඇඳිය නොහැකිය. එනිසා, මතක තබා ගන්න
ක්වෝටර්නියන් එකක් දක්වන්නේ ත්රිමාන කාටිසියානු පද්ධතියක ආකාරයෙන් නොවෙයි (මොකද
ත්රිමාන කාටිසියානු පද්ධතියක එකිනෙකට ලම්භකව අක්ෂ 3ක් පමණක් තිබෙන නිසා). මෙම
රූපික නිරූපණය සඳහා නිකංම කොලය මත එකිනෙකට වෙන් වෙන්ව පෙනෙන ආකාරයට ඇඳි අක්ෂ 4ක්
යොදා ගැනේ. අවශ්ය නම් එම රූපික නිරූපණය චතුර්මාන අවකාශයක (4D) එකිනෙකට
ලම්භක අක්ෂ 4ක් මඟින් කෙරෙන නිරූපණයක් ලෙස “සිතින් මවාගන්න”.
දැන් අපි බලමු ක්වෝටර්නියන් දෙකක් එකතු කරන හා අඩු කරන හැටි. මෙහිදීද
සංකීර්ණ සංඛ්යාවලදී සිදු කළ දේ තවත් පියවරයක් ඉදිරියට යෑමක් පමණි. එනම්, සමාන
කොටස් වෙන වෙනම එකතු කර හෝ අඩු කර දක්වන්නට පමණි තිබෙන්නේ. යම් කොටසක් නැතිනම්
එතැන 0 තිබෙනවා යැයි සිතා (0, 0i, 0j, 0k) සුලු
කරන්න. උදාහරණ කිහිපයක් බලමු.
(-4
+ 3i + j + 12k) + (3 + 8i + 2j + 3k) = -1 + 11i + 3j +
15k
(5 +
2i + 4k) + (4i + j - k) = 5 + 6i + j + 3k
(6 +
2i + 2j +2k) – (i + j - k) = 6 + i + j + 3k
යම් ක්වෝටර්නයක් සාමාන්ය අදිශයකින් ගුණ කළ හැකිය. එවිට එම අදිශ
අගයෙන් ක්වෝටර්නයේ ඇති සෑම සංරචකයක්ම ගුණ කරන්න.
4(2
+ 4i – 2j – 5k) = 8 + 16i – 8j – 20k
ක්වෝටර්නයක් තවත් ක්වෝටර්නයකින් ගුණ කළද හැකිය; මෙය හැමිල්ටන්
ගුණිතය (Hamilton product) ලෙස
හැඳින්වේ. පහත සුලු කිරීම බලන්න. සාමාන්ය
වීජගණිතමය සුලු කිරීමමයි එතැන තිබෙන්නේ. ඊට අමතරව ඉහත සඳහන් කර ඇති ක්වෝටර්නියන්වල
විශේෂිත ලක්ෂණද (ij = k වැනි)
අදාල කරගෙන තිබෙනවා.
H1
= a + bi + cj + dk
H2 = w + xi + yj + zk
H2 = w + xi + yj + zk
H1
x H2 = (a + bi + cj + dk)(w + xi + yj + zk)
= aw + axi + ayj + azk + bwi +bxi2 + byij + bzik + cwj + cxji + cyj2 + czjk + dwk + dxki + dykj + dzk2
= aw + axi + bwi + ayj + cwj + azk + dwk + bw(-1) + cy(-1) + dz(-1) + by(ij) + cx(ji) + bz(ik) + dx(ki) + cz(jk) + dy(kj)
= aw – bx – cy – dz + (ax + bw)i + (ay + cw)j + (az + dw)k + by(k) – cx(ij) – bz(ki) + dx(j) + cz(i) – dy(jk)
= aw – bx – cy – dz + (ax + bw)i + (ay + cw)j + (az + dw)k + byk – cxk – bzj + dxj + czi – dyi
= aw + axi + ayj + azk + bwi +bxi2 + byij + bzik + cwj + cxji + cyj2 + czjk + dwk + dxki + dykj + dzk2
= aw + axi + bwi + ayj + cwj + azk + dwk + bw(-1) + cy(-1) + dz(-1) + by(ij) + cx(ji) + bz(ik) + dx(ki) + cz(jk) + dy(kj)
= aw – bx – cy – dz + (ax + bw)i + (ay + cw)j + (az + dw)k + by(k) – cx(ij) – bz(ki) + dx(j) + cz(i) – dy(jk)
= aw – bx – cy – dz + (ax + bw)i + (ay + cw)j + (az + dw)k + byk – cxk – bzj + dxj + czi – dyi
=
(aw – bx – cy – dz) + (ax + bw + cz – dy)i + (ay + cw + dx – bz)j
+ (az + dw + by – cx)k
ඉහත අවසානයට ලැබී
තිබෙන ප්රතිපලයේ පද විශාල ගණනක් තිබුණත් එයත් ක්වෝටර්නියන් එකක් බව පැහැදිලියිනෙ.
ඉහත ගණනය කිරීම ඉතා සුලු දෙයක් වුවත්, එහි පද ගණන වැඩි නිසා සුලු කිරීම තරමක
හිසරදයක් විය (කොහොමත් මා සුලු කිරීම්වලට බොහෝ කම්මැලියෙකි).
සංකීර්ණ සංඛ්යාවලට
මෙන්ම ක්වෝටර්නියන් සඳහාද ක්වෝටර්නියන් ප්රතිබද්ධය (quaternion conjugate) ඇත. එය * ලකුණකින් සංඛේතවත් කෙරේ.
උදාහරණයක් ලෙස, H = a +
bi + cj + dk යනු
ක්වෝටර්නියන් එකක් නම් එහි ප්රතිබද්ධය පහත දැක්වේ.
H* = a – bi – cj – dk
ක්වෝටර්නියන් ප්රතිබද්ධයක්
නැවත ප්රතිබද්ධ කළ විට නැවත ඔරිජිනල් ක්වෝටර්නියන් එක ලැබේ. එනම්,
(H*)* = a + bi + cj + dk
තවද, පහත ආකාරයේ
සම්බන්දයක්ද පවතී.
එනම්,
ක්වෝටර්නියන් දෙකක ගුණිතයක් ගෙන එහි ප්රතිබද්ධය සමාන වනවා එම ක්වෝටර්නියන් දෙකෙහි
වෙන වෙනම ගත් ප්රතිබද්ධ දෙක පද මාරු කරමින් ගුණ කළ විට.
(H1 x H2)* =
H2*H1*
තවද, යම්
ක්වෝටර්නියන් එකක් එහි ප්රතිබද්ධයෙන් ගුණ කළ විට ලැබෙන්නේ තාත්වික සංඛ්යාවකි. පහත ආකාරයට එම අවසාන
තාත්වික අගය ලැබේදැයි සුලු කොට බලන්න.
(a + bi + cj + dk)x(a – bi – cj –
dk) = a2 + b2 + c2 + d2
ක්වෝටර්නියන් එක එහි
ප්රතිබද්ධයෙන් ගුණ කළ විට ලැබෙන අවසාන පිලිතුර තාත්වික අගයක් බැවින්, න්යාදේශ්ය
න්යාය පිළිපදී. එනිසා පහත ආකාරයට සම්බන්දයක් ලිවිය හැකිය.
H x H*
= H* x H = ||H||2
ඉහත යම් ක්වෝටර්නියන්
එකක් එහි ප්රතිබද්ධයෙන් ගුණ කළ විට ලැබෙන වර්ගපද 4හි එකතුවෙහි වර්ගමූලය ගත් විට,
ඊට එම ක්වෝටර්නියන් එකෙහි norm එක යැයි කියන අතර පහත ආකාරයට එය ලිවිය
හැකිය.
|H| = ||H||
= √(HH*) = √(H*H)
= √(a2 + b2 + c2 + d2)
යම් ක්වෝටර්නියන් එකක නෝර්ම් අගය 1 නම්, එම ක්වෝටර්නියන් එක “ඒකක
ක්වෝටර්නියන්” (unit
quaternion) යැයි හැඳින්වෙනවා. තවද, ඕනෑම ක්වෝටර්නියන් එකක් ගෙන එය එහි නෝර්ම් එකෙන් බෙදූ විට (එනම්,
H / ||H|| ), එම
ගණිතමය ක්රියාව quaternion
normalization ලෙස හැඳින්වෙනවා.
ක්වෝටර්නියන් එකක තාත්වික කොටස හෙවත් අදිශ කොටස වෙනමත් අතාත්වික කොටස
හෙවත් දෛශික කොටස වෙනමත් ගෙන පහත ආකාරයට නිරූපණය කළ හැකිය. පසුව
විස්තර කරන සමහර ගණිත කර්ම විස්තර කිරීමේදී මෙම නිරූපණය යොදා ගැනීමෙන් එම සූත්ර
සරලව පෙනේ. මෙහිදී v = bi + cj
+ dk වේ.
H = a + bi + cj + dk à H = a + v
ක්වෝටර්නියන් එකක් e පාදයේ බලයකට නැංවිය හැකියි පහත ආකාරයට. ||v|| යනු
දෛශික කොටසේ නෝර්ම් එක වේ. එනම්, ||v|| = √( b2 + c2
+ d2) වේ.
තවද, ක්වෝටර්නියන් එකක ලඝු පහත ආකාරයට සෙවිය
හැකිය.
ඔබ දන්නවා සංකීර්ණ සංඛ්යාවක් a + bi යන ආකාරයට අමතරව පහත පෙන්වා තිබෙන විදියට තවත්
ආකාර දෙකකින් නිරූපණය කළ හැකියි.
C = r(cosθ
+ isinθ) - ධ්රැවීය නිරූපණය (polar)
C = reiθ - ඔයිලර් නිරූපණය (Euler)
ඉහත අඩිපාර දිගේ යමින්ම ක්වෝටර්නියන් එකක්ද එම
නිරූපණ ක්රම දෙකෙන්ම පහත ආකාරයට ලිවිය හැකිය.
H = ||H||(cosθ + ňsinθ)
H =
||H||eňθ
ඉහත
සූත්ර දෙකෙහි හමුවන ň යනු දෛශික කොටස (v) එම දෛශික
කොටසෙහි නෝර්ම් එකෙන් (||v||) බෙදූ විට ලැබෙන අගය වේ (ň = v / ||v||). ක්වෝටර්නියන්
සඳහා ඔයිලර් හා ධ්රැවීය නිරූපණයන් ලබා ගත් අයුරු දැන් කෙටියෙන් බලමු. ගණිතයේ
හමුවන ශ්රේණි (series) හි පවතින මූලික සිද්ධාන්තයක් ගැන
පලමුව බලමු. එනම්,
ඉහත
පෙන්වා තිබෙන්නේ ඝාතීය ශ්රිතය (exponential
function) ශ්රේණියක් ලෙස දක්වන ආකාරයයි. මෙහි x යන දර්ශක පදයට තාත්වික, අතාත්වික, සංකීර්ණ, හෝ ක්වෝටර්නියන් සංඛ්යාවක්
ආදේශ කළ හැකිය. ඒ අනුව, ක්වෝටර්නියන් සංඛ්යාවක් (H) ආදේශ
කර එය ඉහත ශ්රේණිය ඇසුරින් සුලු කර බලමු. එහිදී ක්වෝටර්නියන් සංඛ්යාව H =
a + bi + cj + dk යන සාමාන්ය ස්වරූපය
වෙනුවට H = a + v යන ස්වරූපය යොදා ගමු. තවද, exey
= ex+y යන සම්බන්දතාවද මෙහිදී යොදා ගැනේ.
එබැවින්, eH = ea+v = eaev ලෙස ගත හැකි අතර දැනට ea කොටස අමතක
කර ev යන කොටස ගැන සිතමු.
තවද,
v = bi
+ cj + dk
v2 = (bi + cj + dk)(bi + cj + dk) = -b2 – c2 – d2 = -(b2 + c2 + d2) = -||v||2
v2 = (bi + cj + dk)(bi + cj + dk) = -b2 – c2 – d2 = -(b2 + c2 + d2) = -||v||2
එනිසා,
පහත ආකාරයේ රටාවක් පවතිනවා.
v2
= -||v||2 , v3 = -||v||2v , v4 =
||v||4 , v5 = ||v||4v , v6 = ||v||4(-||v||2
) = -||v||6 , …
ඉහත
ශ්රේණියට ආදේශ කළ විට,
ඔබ
දන්නවා සයින්, කොස් ආදි ත්රිකෝණමිතික ශ්රිතද ඝෘතීය ශ්රේණි ඇසුරින් පහත ආකාරයට
නිරූපණය කළ හැකිය.
ඒ
අනුව මීට ev
හි ඉහත අවසාන පේලියට සයින් හා කොස් ශ්රිත ආදේශ කර පහත ආකාරයට
සැකසිය හැකියි.
දැන්
මුලින් අමතක කර දැමූ ea
කොටස ආදේශ කර පහත ආකාරයට ක්වෝටර්නියන් එකක් සඳහා සූත්රය ලිවිය
හැකිය.
තවද,
H = a + v ලෙස සලකන නිසා, a, v පද දෙකෙහිම හරය හා ලවය ||H||
වලින් බෙදා, v පදයේ හරය හා ලවය නැවත ||v||
වලින් බෙදූ විට පහත ආකාරය ලැබේ.
H = a
+ v සේම ||H||2 = a2 + ||v||2
වේ. එනිසා, සමීකරණයේ දෙපසම ||H||2 මඟින් බෙදීමෙන් පහත ආකාරයට ලැබේ.
ඉහත
සූත්රය ත්රිකෝණමිතික සාම්යයක් වන sin2(x)
+ cos2(x) = 1 යන්නට අනුරූප වේ. එනිසා, කෝණය රේඩියන්
0ට වඩා වැඩි රේඩියන් 2π වඩා අඩු සීමාව තුල තිබිය යුතුය යන
කොන්දේසිය යටතේ ඉහත ක්වෝටර්නියන් සමීකරණය පහත ආකාරයට සයින් හා කොස් ඇසුරින් (කෝණයක්
ඇසුරින්) අර්ථ දැක්විය හැකියි.
මෙවිට
පහසුවෙන්ම H =
||H||eňθ යන සූත්රයද සාධනය වේ. ඉහත
සම්බන්දතා නිසා පහත ආකාරයටද සම්බන්දතා 2ක් පවතින බව පහසුවෙන්ම පෙනේ.
a = ||H||(cosθ)
v = ||H||( ňsinθ)
ක්වෝටර්නියන්
එකක ධ්රැවීය හෝ ඔයිලර් නිරූපණය යොදා ගෙන පහසුවෙන්ම ක්වෝටර්නියන් එකක් බලයකට
නැංවිය හැකිය.
Ht = ||H|| t eňtθ
Ht =||H||t (costθ
+ ňsintθ)
ක්වෝටර්නියන්
දෙකක් අතර තවත් ආකාරයක ගුණිතයක් අර්ථ දැක්විය හැකියි dot product
(තිත් ගුණිතය)
හෙවත් inner product ලෙස. මෙම
ගුණිතය තිතක් මඟින් සංඛේතවත් කරන අතර, හැමිල්ටන් ගුණිතය කතිරයක් මඟින් හෝ කිසිම
සලකුණක් නැතිව (H1 x H2 හෝ H1H2
ලෙස) සාමාන්යයෙන් සංඛේතවත් කෙරෙනවා.
තිත් ගුණිතයෙන් ලැබෙන්නේ තාත්වික සංඛ්යාවකි.
H1
. H2 = (a + bi + cj + dk).(w + xi + yj + zk)
= aw + bx + cy + dz
තිත් ගුණිතය ඇසුරින් අපට හැකියි දී තිබෙන
ක්වෝටර්නියන් දෙකක් අතර කෝණය සොයා ගන්නට පහත සූත්රයෙන්.
ක්වෝටර්නියන් එකක ප්රතිලෝමය (inverse), H-1 ලෙස
නිරූපණය කරන අතර, එය පහත ආකාරයට ගණනය කළ හැකිය (ඇත්තටම
මෙම සූත්රයේ සාධනය ඉතාම පහසු අතර, මෙතෙක් උගත් කරුණු ඔස්සේ පේලි දෙකකින් පමණ එය
සාධනය කළ හැකිය).
ක්වෝටර්නියන් එකක් තවත් ක්වෝටර්නියන් එකකින්
බෙදිය හැකිය. මේ සඳහා භාජකය (divisor) ලෙස පවතින ක්වෝටර්නියන්
එකේ ප්රතිලෝමයෙන් අනෙක් ක්වෝටර්නියන් එක හෙවත් භාජ්යය (dividend) ලෙස පවතින ක්වෝටර්නියන් එක ගුණ කළ හැකිය.
H1 / H2 = H1 H2-1
බහුලවම ක්වෝටර්නියන් පරිගනක ගේම්ස් සෑදීමේදී
රූප/ඇනිමේෂන් සඳහා යොදා ගැනෙන බව පවසනවා (මා කොම්පියුටර් ගේම් හෝ ගේම් ප්රෝග්රැමිං
හෝ ගැන කිසිත් නොදන්නා නිසා ඒ ගැන විස්තර කරන්නට බැරිය). එහෙත් එහිදිත් ඇත්තටම
ගණිතය තුල ඉගැන්වෙන ක්වෝටර්නියන් සංකල්පයම නොව, එම සංකල්පයෙහි යම් කුඩා කොටසක්
(එනම් යම් කිසි අගයන් 4ක් තනි ඒකකයක් හෙවත් පරිගනක භාෂාවෙන් කියනවා නම් කොම්පොසිට්
වේරියබල් එකක් ලෙස නිරූපණය කිරීමට හා හැමිල්ටන් ගුණිතය) පමණක් එහිදී යොදා ගැනෙන බව
විමසීමේදී පෙනෙනවා. තවද, සංකීර්ණ සංඛ්යා පද්ධතිය ක්වෝටර්නියන් මඟින් විස්තීර්ණ
කෙරුණා සේම, ක්වෝටර්නියන්ද තවදුරටත් විස්තීර්ණ සංඛ්යා පද්ධතියක් බවට පත් කෙරෙනවා octonion
නම් ගණිත සංකල්පය මඟින් (මෙහිදී අෂ්ටමාන අවකාශයක්
පවතී). බලන් ගියහම මෙහි විස්තීර්ණ කිරීමේ ඉවරයක් නැත.














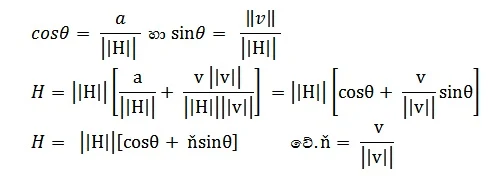

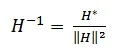
මමත් මේ ගැන ලිපියක් ලියන්න හිතුවා.
ReplyDeleteචතුෂ්ටය කියන නම දැනගත්තේ අදයි.
මම ඔය ගැන දැනගත්තේ ත්රිමාණ ෆ්රැක්ටල් මෝස්තර සෑදීමට උත්සාහ කරන විටයි.
එහිදී split complex number කියා දෙයකුත් හමුවුනා.
තව කරුණක් එකතු කරනවා නම් හැමිල්ටන් කියන ගණිතඥයාට මුලින්ම අවශ්ය වුනේ අතාත්වික විචල්ය දෙකක් ඇති සංඛ්යා පද්ධතියක් නිපදවීමටයි.
එය කල නොහැකි වූ නිසා ඔහු චතුෂ්ට නිර්මාණය කලා.
මේ ලිපියේ පොඩි අඩුපාඩුවක් තියෙනවා. මෙතන
ධ්රැවීය නිරූපණයේ සහ ඔයිලර් නිරූපණයේ θ කෝණය ගන්න ආකාරය දැක්විය යුතුයි.
ඒ වගේම ලිපියේ අගට චතුෂ්ටවල
sin, cos, tan, asin, acos, cosh, යනාදී ගණිත කර්ම වල සූත්ර මාලාවකුත් ඉදිරිපත් කලොත් හොඳයි.
මම visual basic.net වලින් සංකිර්ණ සංඛ්යා, දෛශික, චතුෂ්ට වල ගණිත කර්ම කිරීමට කල කේත කොටසක් මේ සමඟ ඉදිරිපත් කරනවා.
එය යොදාගෙන සාමාන්ය සංඛ්යා හසුරවන ආකාරයටම ඉහත ගණිත සංකල්ප හැසිරවිය හැකියි.
https://www.dropbox.com/s/sbq6fup0rfvdnhw/Math.vb
කෝණ ලබා ගත් අයුරු මා ඇතුලත් කළා.
Deleteනලින් ද සිල්වා මහතා ගැන ඔබේ අදහස කුමක්ද ? ඔහු ඉදිරිපත් කරන කරුණු පිළිගැනීමට හැකිද ?
ReplyDeleteපාසල් යන කාලයේ ඔහුගේ චින්තන පර්ෂදය නම් සංවිධානයට යම් කලක් මා සම්බන්දව සිටියා... ඒ සමයෙහිද මා ඔහු ගැන ඇති කරගත් හැඟීම ඍණාත්මක වේ (එකල ඔහුව සේවයෙන් නෙරපා සිටි සමයයි). සමහරවිට ඔහු තුල ඇති විශිෂ්ට විද්යා දැනුම නිරන්තරයෙන්ම ඔහුව වෙලා සිටින ඔහුගේ (මා සිතන පරිදි) මානසික ව්යාකූලතාවත් එනයින්ම ඔහුට හිමිව ඇති අඳුරු පෞරුෂයත් නිසා රාහුට හසු වූ චන්ද්රයකු සේ මා ඔහු දකිනවා. තවද, ඔහු කුමන්ත්රණ න්යායවාදියකු සේත් උග්ර ජාතිවාදියකු සේත් මා දකිනවා. ඔහු ඉදිරිපත් කරන මතවාද විද්යාත්මක නොව දාර්ශනිකයි. එනිසා විද්යා ආචාර්ය කෙනෙකු වුවත් ඔහුගේ එළඹුම් (සංවාද තුල) ආගමික දර්ශනවාදියකුට බොහෝ සමානය. කොටින්ම කියතොත් ලංකා සමාජයේ චින්තන අවගමනයකට ඔහුගේ මතවාද (සමාජදේශපාලන මෙන්ම විද්යාව සම්බන්දයෙන්) ගෙන යන බව කීමට සිදු වෙනවා.
Deleteඔහු හා ඔහුගේ අනුගාමිකයන් මේ දිනවල තනි අශ්වයෙකුගේ තරගයක නිරත වී සිටිනවා. ගණිතය, දර්ශනය යොදාගනිමින් කේතනය කරනු ලැබ ඒ හා ඔවුන්ගේ අන්තවාදී මතවාද එක්කොට ජනයාට නිවැටහෙන ගැඹුරක් ඔවුන්ගේ කියුම් තුළ අන්තර්ගත බව ඒත්තු ගන්වමින් සමජ ජාලා සහ පුවත්පත් වලින් ඔවුන් සමාජගත වනවා. ඔවුන්ට පිළිතුරු දීමට ලංකාවේ දැනමුතු පුද්ගලයන් ඉදිරිපත් විය යුතුයි කියා මා සිතනවා
ReplyDeleteඑහි කිසිදු වරදක් නැත. බුද්ධිමත් සමාජයකට එකිනෙකට වෙනස් හා ගැටෙන මතවාදයන් රාශියක් තිබීම වැදගත් වේ. නැටුමෙන් වැයුමෙන් සුපර්ස්ටාර්ලා වීමේ සිහින ව්යාධියෙන් පෙලෙන පිරිසකුත් උන්ව චූන් කරන අමන ප්රේක්ෂක රොත්තකුත් ඉන්න රටකට ඇත්තටම මොනයම් හෝ මතවාද මත තර්ක විතර්ක කරන පිරිස වැඩි වේ නම් එය සතුටට හේතුවකි.
Deleteඔබ හරි
ReplyDeleteCryptocuruncy (ගුප්ත කේත මුදල් ?) ගැන ලිපි පෙළක් ලියන්න පුලුවන්ද ?
ReplyDeleteමට ඒ ගැන එතරම් වැටහීමක් නැත... කෙසේ වෙතත් එය ඉතාම අවදානම් සහගත වටිනාකම් ව්යවහාරයකි; තරමක සූදුවකි. ෆොරෙක්ස් සූදුව, බිට්කොයින්/ක්රිප්ටොකරන්සි සූදුව වැනි දේ ප්රචලිත වන දේවල් මා එනිසා ලියන්නේ නැත.
Deleteඅපිට සංඛ්යා පද්ධති විස්තීර්ණය කරන්න පුලුවන්. තාත්වික සංඛ්යා -> සංකීර්ණ සංඛ්යා -> quaternion -> octonion -> ...
ReplyDeleteමේව විස්තීර්ණය වෙන්නෙ pattern එකකට. මේ එකිනෙකට වෙනස් අපූරු සංඛ්යා නිරූපණය කිරීමේදී අප යොදාගත යුතු මාන ගණන පහත සරල සමීකරනයෙන් පැහැදිලි කරනවා.
D=2^n
D මාන ගණන
n කුමන සංඛ්යාවක්ද යන වග (තාත්වික,සංකීර්ණ,...)
n කියන්නෙ නිඛිලයක්නේ.. මේක බැලුවම මට හිතෙනව ගණිතයත් quantization වෙලාද කියා... මෙහෙම බැලුවම හිතෙනවා continuum hypothesis වැරදී කියා... මේ දෙක අතර සම්බන්ධතාවයක් නැති බව ඇත්ත. ගණිතය කියන්නේ continuous දෙයක්නේ. නමුත් මේ අමුතුම වර්ගයේ quantization එක අර මං කියපු simulation ෆැන්ටසිය (fermi paradox) හරි කියන පැත්තට සාක්ෂියක් ලෙස ගන්න පුලුවන්..
https://blog.tekcroach.top/2019/05/blog-post.html?showComment=1557211739427&m=1#c6286420739451597677
පිස්සුම පිස්සු විකාර (සමහරවිට ගොං) අදහසකට නැවතත් සමාවෙන්න... :)
අනුන්ගේ ඕපදූප හෝ කුනුහබ්බ හෝ නොවන ඕනම දෙයක් මා මෝඩ යැයි සලකන්නේ නැත. ඇත්තටම ඔබ කියන සමහර දේවල් ගැන මට වැටහීමක් නැත. ඊට හේතුව ඔබ කියන දේ මෝඩ වීම නොව ඔබ ඉතා කෙටියෙන් එය පැවසීම විය හැකියි. සංඛ්යා පද්ධති හා මාන අතර ඓන්ද්රිය සම්බන්දතාවක් මට නම් දැනෙන්නේ නැත. D=2^n යන්න තාත්වික, සංකීර්ණ සංඛ්යා සඳහා යොදා බලන්න ඔබ කියන පරිදි මාන ලැබෙනවාද කියා.
Deleteඔවු.. එය ඇත්තෙන්ම වැඩ කරනවා. මං හිතන්නෙ මං ඒක පැවසූ ආකාරය වැරදි නිසා ඔබට ඒ ගැන වැරදි වැටහීමක් ඇතිවුණා කියලා.
Deleteතාත්වික සංඛ්යාවක් "නිරූපණය කිරීමට අවශ්ය මාන ගණන" D=2^0=1
සංකීර්ණ සංඛ්යාවක් """ D=2^1=2
quaternion """ D=2^2=4
octonion """" D=2^3=8
මං ගොඩක් දේ කෙටියෙන් තමා පවසන්නේ. මොකද මගේ හිතට එකවර් අදහස් සිය ගණනක් ගලා එනවා. මට ඒ සියල්ලම ටයිප් කරන්න ටයිපින් ස්කිල් එක මදි.. හහා... ඊලග කොමෙන්ටුව බොහෝ විට රචනාවක් වේවි. මොකද මට අද නින්ද ගියෙ නෑ.. හහා..
ආ... දැන් පැහැදිලි වුණා :) මං හිතන්නේ ඔබේ මීට පෙර කමෙන්ටුවෙනුත් ඒක පැහැදිලිව තිබුණා (නමුත් මං එය ඉක්මනින් කියවාගෙන ගිය නිසා හෝ මගේ ප්රොසෙසර් එක (මොලය) එච්චර පවර්ෆුල් නැති නිසාදෝ එය තේරුම් ගන්න බැරි වුණා). හාහා... ඔබේ සිතට එන සියලුම අදහස් පොතක ලියා තබන්න. කවුද දන්නේ ලෝකය හොල්ලන යම් යම් සොයා ගැනීම් ඒ තුලින් මතු වේවිද කියලා...
Deleteඉතිං n යනු නිඛිලයක්නේ.. ඒකත් quantized වෙලා වගේ මට පේන්නේ.. ගණිතය යනු සාමාන්යයෙන් continuous දෙයක්නේ.. නමුත් මේක continuous නෑ. ඉතිං මේක මා කලකට පෙර පැවසූ සිමියුලේෂන් ෆැන්ටසිය හරි කියන පැත්තට සාක්ෂියකි... අනික ගොඩක් තියරි පරීක්ෂණාත්මකව ඔප්පු කිරීමට පෙර ගණිතයෙන් ඔප්පු කරලා තියෙනවානේ ඉතිං ස්ට්රිං තියරිටත් ඒක පොදු වෙන්න පුලුවන් නේද??
Deleteහහා... ඒ අදහස කදිමයි.. මං දැනටත් notepad එකේ මගේ අදහස් ලියා තිබෙන්නේ... මා නව නිර්මාණ අදහසකුත් කියන්නට කැමතී. මේකයි කතාව මං හිතන්නෙ මේ බ්ලොගය බලන හැමෝම එක්වරක් හරි මේ අත්දැකීමට මුහුණ දීල ඇති. අපිට රෑ නිදාගනිද්දී fan එකක්/ ac එකක් අවශ්යයිමනේ... හැබැයි සමහර දවස් වලට උදේ නැගිටින්න වෙන්නෙ සුපිරියටම වේලිලා උගුරත් මොකක්ද වෙලා.. හරි හරි ටයිමර් තියෙනවා තමයි.. ඒත් ඉතිං ටයිමරෙ වෙලාවටම නින්ද යන්නෑනේ.. අනික සමහර අසනීප රෑට උත්සන්න වෙනවා.. සහ + ඩිස්ටිඩිඩිං වැඩ.. ඉතිං මට හිතුනා නව නිර්මාණ අදහසක් අතේ බැදල තියෙන fitness tracker එකක් A/C එකකට මොකක් හරි ගැජට් එකකින් connect කරල නින්දට සුදුසු පරිසරයක් (උෂ්ණත්වයක්) කාමරය තුල නිර්මාණය කළොත් ඒක හොඳයි නේද කියලා.. මේක හරි සරල අදහසක්.. medical student කෙනෙකුටයි software student කෙනෙකුටයි උනත් එකතුවෙලා ලේසියෙන් මේක හදන්න පුලුවන් අඩු වියදමකින්..(ගැජට් එක හදන්න විතරයි වියදම යන්නේ) මේක හොඳ invester කෙනෙක් සෙට් කරන් හොඳ publicity එකක් දුන්නොත් නැගල යයි.. හහා... කැමති එක්කෙනෙක් ඉන්නවනම් try කරල බලන්න.. අපිටත් ප්රතිපල කියන්න.
This comment has been removed by the author.
Deleteඔබ පෙන්වා දුන් සරල සූත්රයෙන්/සම්බන්දතාවෙන් දක්වන්නේ යම්කිසි ගතිලක්ෂණ සමූහයක් තෘප්ත කරන සේ සකස් කර ගත් යම් සංඛ්යා පද්ධතියක පවතින තත්වයක්නෙ. එහෙත් බහුමාන පවතී නම්, එම මානවලට ඔබ කියනා ආකාරයේ සීමාවක් ගැන කියන්නේ නැත. එනිසා මාන quantized වී පවතී යැයි කිව නොහැකිය. තවද, ගනිතය continuous හෝ digital (quantized) ලෙස ලේබල් කළද නොහැකිය. මේ හැමදේටම ගනිතය තුල ඉඩක් ඇත.
Deleteඔබේ නිර්මානයත් හොඳයි. මං ඊට වෙනත් අදහසකුත් පවසන්නම්. ඇඳක් මතදී මෙට්ටය මත ස්පර්ශව පවතින ශරීර අංග කාලයත් සමග රත් වෙනවානෙ. අපට සැප නින්දකට ඇත්තටම බාධා කරන්නේ එයයි. එනිසා හැකි නම් ඇඳ මෙට්ටය මතුපිට පමනක් යම් සිසිලසක් පවත්වාගෙන යා හැකි ආකාරයේ උපක්රමයක් යෙදිය හැකි නම් ඉන් විශාල ශක්තියක්ද ඉතිරි කර ගත හැකි අතර පැය ගණනක් දූවිලිද සහිත වා රැලි නාසය හරහා ගොස් ඇති වන "සෙම ගතිය" පවා අවම කර ගත හැකි වේවි.