සන්නිවේදනය හා ආධුනික ගුවන් විදුලි සේවය (Amateur radio) 22

Angle Modulation

කෝණ මූර්ජනය යනු සංඛ්‍යාත මූර්ජනය හා කලා මූර්ජනය යන දෙකටම කියන පොදු නමයි. ඇත්තටම මෙම මූර්ජන ක්‍රම දෙකම ඉතා සමානය (ඉතා සමාන මිස සර්වසම නොවේ). තරංගයක් (රේඩියෝ හෝ වෙනත්) Asin(θ) යන සරල සූත්‍රයෙන් (හෝ ඉන් ව්‍යුත්පන්න කළ Asin(ωt) හෝ Asin(2πft) යන සූත්‍රයකින්) නිරූපණය කළ හැකි බව ඉගෙන ගත්තනෙ. එහි A යනු උපරිම විස්තාර අගය වන අතර කෝණ මූර්ජනයේදී (එනම්, සංඛ්‍යාත මූර්ජනයේදී හෝ කලා මූර්ජනයේදී) එය නියතව පවතින අතර, සයින් ශ්‍රිතය තුල පවතින කෝණය (θ) බුද්ධි සංඥාවට අනුරූපව විචලනය කෙරේ.

කෝණ අගයම (θ) සංඛ්‍යාතය සහිත ප්‍රකාශයක් බවට පත් කළ හැකියි θ = 2πft ලෙස. එවිට කෝණය වෙනස් වෙනවා යනු සංඛ්‍යාතය (f) වෙනස්වීමක් ලෙස දැක්විය හැකියිනෙ. මෙන්න මෙම අවස්ථාව තමයි සංඛ්‍යාත මූර්ජනය ලෙස හැඳින්වෙන්නේ. තවද, කෝණ අගයම θ = 2πft + ϕ ලෙස අමතරව කලාව හඟවන පදයක් (ϕ) සහිතවත් ලිවිය හැකියි. එවිට, කෝණය වෙනස් වෙනවා යනු කලාව (ϕ) වෙනස්වීමක් ලෙස දැක්විය හැකියිනෙ. එය තමයි කලා මූර්ජනය ලෙස හැඳින්වෙන්නේ. ඉදිරියේදී සංඛ්‍යාත හා කලා මූර්ජන දෙක ගැන වෙන වෙනම සලකා බලන විට තවදුරටත් එය පැහැදිලි වේවි.

සංඛ්‍යාත මූර්ජනය

බුද්ධි සංඥාවට අනුරූපව වාහක තරංගයේ සංඛ්‍යාතය වෙනස් කිරීම මෙහිදි සිදු වේ. වාහකයේ විස්තාර අගය වෙනස් නොවී නියතව පවතී.

සුපුරුදු ලෙසම, සෑම මූර්ජන ක්‍රමයකදීම සිදුවන කාර්යන් දෙක මෙහිත් සිදු වේ - එනම්, බේස්බෑන්ඩ් සංඥාව අපට කැමති ඉහල සංඛ්‍යාත පරාසයකට ඔසවා තැබීම හා බුද්ධි සංඥාව කුමන හෝ ක්‍රමයකින් වාහක සංඥාව තුලට කා වැද්දීම. මේ දෙක සිදුවන අන්දම දැන් බලමු.

ලෝකල් ඔසිලේටරයෙන් නිපද වෙන්නේ පුරුදු ලෙසම අපට අවශ්‍ය අධිසංඛ්‍යාත වාහක තරංගයයි. එහි විස්තාරය මෙන්ම සංඛ්‍යාතයද නියතයි. සංඛ්‍යාත මූර්ජනයේදී මෙම සංඛ්‍යාතය resting frequency හෝ center frequency හෝ nominal carrier frequency ලෙස හැඳින්වේ.

දැන් සංඥා/බුද්ධි තරංගය මූර්ජකය තුලට ඇතුලු වේ (වාහක තරංගයත් ඒ සමගම ඊට ඇතුලු වේ). එවිට සිදු වන්නේ සංඥාවේ වෝල්ටියතා අගය අඩු වැඩි වන විට, ඊට අනුරූපව වාහක තරංගයේ සංඛ්‍යාතයද අඩු වැඩි වීමයි. විශේෂයෙන් මතක තබා ගන්න සංඥා තරංගයේදී සලකා බලන්නේ එහි විස්තාර අගයේ (එනම් වෝල්ටියතාවේ) අඩු වැඩිවීම වන අතර, වාහක තරංගයේදී සිදු වන්නේ එහි සංඛ්‍යාතයේ (හර්ට්ස් අගයේ) අඩු වැඩි වීමයි.

සංඥාවේ වෝල්ටියතාව ක්‍රමයෙන් වැඩි වන විට, වාහකයේ සංඛ්‍යාතයද ඊට අනුරූපව ක්‍රමයෙන් වැඩි වේවි. සංඥාවේ අගය ක්‍රමයෙන් අඩු වන විට, වාහකයේ සංඛ්‍යාතයද ඊට අනුරූපව ක්‍රමයෙන් අඩු වේවි.

ඇත්තටම ඊට විරුද්ධවද එය සිදු කළ හැකියි. එනම්, සංඥාවේ වෝල්ටියතාව ක්‍රමයෙන් වැඩි වන විට වාහකයේ සංඛ්‍යාතය ඊට ප්‍රතිලෝමව අනුරූප වන පරිදි (හෙවත් සංඛ්‍යාතය ක්‍රමයෙන් අඩු වන පරිදි) හා, සංඥා වෝල්ටියතාව ක්‍රමයෙන් අඩු වන විට වාහක සංඛ්‍යාතය ක්‍රමයෙන් වැඩි වන පරිදි එය සිදු කළ හැකියි.

අප මෙතැන් සිට සලකා බලන්නේ පළමු ක්‍රමය වන සංඥාවේ වෝල්ටියතාවට අනුලෝමව වාහක සංඛ්‍යාතය අඩු වැඩි වන ක්‍රමයයි.

ඉහත සිදුවීම උදාහරණයකින් සලකා බලමු. වාහක තරංගයේ සංඛ්‍යාතය මෙගාහර්ට්ස් 100 යැයි සිතමු. පැහැදිලි කිරීමේ පහසුව සඳහා, සංඥා තරංගය කිලෝහර්ට්ස් 1ක සයිනාකාර තරංගයක් ලෙස සිතමු (ඔබ මේ වන විට හොඳින්ම දන්නවා ප්‍රායෝගික සංඥා තරංගය අක්‍රමවත් හැඩයක් සහිත බවත්, එම අක්‍රමවත් හැඩය ෆූරියර් න්‍යාය අනුව සංඛ්‍යාතයන් වෙනස්, සයිනාකාර තරංග සෙට් එකකින් නිරූපණය කළ හැකි බවත්). මෙගාහර්ට්ස් 100 තරංගයක් සඳහා වන කාලාවර්තය තත්පර 1/100,000,000 හෙවත් නැනෝතත්පර 10කි. ඒ කියන්නේ එම සංඛ්‍යාතයේ එක් තරංගයක් නැනෝතත්පර 10ක කාලයක් පුරාවට පවතිනවා. එලෙසම කිලෝහර්ට්ස් 1ක සංඛ්‍යාතයෙන් යුතු තරංගයක් සඳහා වූ කාලාවර්තය වන්නේ තත්පර 1/1000 හෙවත් මිලිතත්පර 1කි. එවිට, කිලෝහර්ට්ස් එකේ සංඛ්‍යාතයේ එක් තරංගයක් ඇති වී නැති වන විට, මෙගාහර්ට්ස් සියයේ තරංග ලක්ෂයක් ඇති වී නැති වී යයි.

එක් සම්පූර්ණ සංඥා තරංගයක පවතින විස්තාර අගය ස්ථාන 4000කදී වෙන වෙනම සලකා බලමු (පහත රූපය). යම් තරංගයක මෙලෙස ස්ථාන කිහිපයක් වෙන වෙනම ගෙන අගය මැනීම sample කරනවා යැයි කියනවා. ඒ අනුව මෙම අවස්ථාවේදී තරංගය අපි ස්ථාන 4000 කදී සාම්පල් කරනවා. සම්පූර්ණ සාම්පල් 4000ම ඇඳීමට අපහසු බැවින් පහත රූපයේ ඇඳ තිබෙන්නේ එවැනි සාම්පල් කිහිපයක් පමණි.

එම තරංගයේ V_pp අගය වෝල්ට් 2ක් ලෙසද සිතමු. එවිට, වෝල්ට් 0 හඟවන තිරස් x අක්ෂයෙන් ඉහලට උපරිම විස්තාරය වෝල්ට් 1ක්ද, එම අක්ෂයේ සිට පහලට (ඍන පැත්තට) උපරිම විස්තාරය වෝල්ට් 1ක්ද වේ. එවිට සාම්පල් 4000න් හරි අඩක් තිරස් අක්ෂයෙන් ඉහලද, අනෙක් අඩ ඉන් පහලද පවතීවි. තවද, තරංග ප්‍රස්ථාරය ශූන්‍ය අගයේ සිට එහි උපරිම අගය දක්වා වූ පරාසය තුල සාම්පල් 1000ක් ඇත (එනම්, තරංගයේ සෑම අංශක 90ක පරාසයක් සඳහා සාම්පල් 1000 බැඟින් ඇත). ඒ කියන්නේ එක් සාම්පලයක කාලය වන්නේ මුලු තරංග කාලයෙන් (ආවර්ත කාලයෙන්) 1/4000 වේ. කිලෝහර්ට්ස් 1ක තරංගයක් අප දැන් සලකා බලන බැවින්, ඉහත සෙවූ පරිදි එහි කාලාවර්තය මිලිතත්පර 1ක් බැවින්, එක් සාම්පලයක කාලය (sample duration) මිලිතත්පර 1/4000 හෙවත් මයික්‍රොතත්පර 1/4ක් හෙවත් නැනෝතත්පර 250කි.

ආරම්භක ස්ථානය පිහිටා තිබෙන්නේ තරංගය තිරස් අක්ෂය කපන ස්ථානයෙහි බැවින් එතැන වෝල්ටියතාව 0 වේ. ඊට පසුව ලකුණු කර ඇති සාම්පලයේ වෝල්ටියතාව වෝල්ට් 0.001 හෙවත් මිලිවෝල්ට් 1 යැයි සිතමු. ඊට පසුව ඇති සාම්පලයේ වෝල්ටියතාව මිලිවෝල්ට් 2 යැයිද, ඊළඟ එකේ මිලිවෝල්ට් 3 යැයිද, ආදි ලෙස 1000 වැනි සාම්පලයේදී (එනම්, තරංගය උපරිම විස්තාරයේ පවතින විට), එතැන මිලිවෝල්ට් 1000 හෙවත් වෝල්ට් 1ක් වේවි (මා මෙහි උවමනාවෙන්ම පැහැදිලි කිරීමේ පහසුව තකා යම් සරල කිරීම් කර ඇත).

දැන් අපි සිතමු එම සංඥාව මෙගාහර්ට්ස් 100 ක වාහක තරංගය සමග සංඛ්‍යාත මූර්ජනය සිදු කරනවා කියා. තවද, සංඥාවේ සෑම මිලිවෝල්ට් 1ක් සඳහාම වාහක සංඛ්‍යාතය හර්ට්ස් 10කින් වෙනස් වෙනවා යැයි සිතමු.

එවිට, සංඥාවේ ආරම්භයේදී මිලිවෝල්ට් 0 නිසා, වාහක සංඛ්‍යාතය කිසිදු වෙනසක් ඇති නොවේ. ඒ කියන්නේ මෙම අවස්ථාවේදී වාහක සංඛ්‍යාතය මෙගාහර්ට්ස් 100 හෙවත් හර්ට්ස් 100,000,000 වේ.

ඊට සුලු මොහොතකට (එනම් නැනෝතත්පර 250ක්) පසුව සංඥාව මිලිවෝල්ට් 1ක් ගනී. ඉතිං එම මිලිවෝල්ට් එකක වැඩිවීම නිසා වාහක සංඛ්‍යාතය එහි රෙස්ටිං සංඛ්‍යාතයේ සිට හර්ට්ස් 10කින් වැඩි වේවි. ඒ අනුව, මෙම අවස්ථාවේ වාහක සංඛ්‍යාතය 100,000,000+10 = 100,000,010 දක්වා වැඩි වේ.

ඊළඟ සාම්පලයේදී මිලිවෝල්ට් 1 සිට 2 දක්වා වැඩි වෙනවනෙ. ඒ කියන්නේ නැවතත් මිලිවෝල්ට් 1ක වෙනසකින් වැඩි විය. එනිසා, වාහක සංඛ්‍යාතය නැවතත් හර්ට්ස් 10කින් වැඩි වේ. එවිට දැන් වාහකයේ සංඛ්‍යාතය ඊට පෙර සංඛ්‍යාතය වන 100,000,010 ට වඩා 10කින් වැඩිය (එනම්, 100,000,010+10 = 100,000,020).

එලෙස සාම්පල් 1000කදී (එවිට සංඥාවේ වෝල්ටියතාව මිලිවෝල්ට් 1000 වෙනවානෙ) වාහක සංඛ්‍යාතය සෑම මිලිවෝල්ට් 1කටම හර්ට්ස් 10 බැඟින් වැඩි වීම නිසා හර්ට්ස් 1000x10 = 10,000 කින් වැඩි වේ. ඒ කියන්නේ උපරිම විස්තාර අගයේදී වාහක සංඛ්‍යාතය 100,000,000+10,000 = 100,010,000 හෙවත් මෙගාහර්ට්ස් 100.01 වේ.

එලෙසම උපරිම විස්තාරයේ සිට ක්‍රමයෙන් නැවත x තිරස් අක්ෂය දක්වා (එනම් ශූන්‍ය වෝල්ටියතාව දක්වා) විස්තාර අගය අඩු වන විට, ඊට අනුරූපවම වාහක සංඛ්‍යාතයද ක්‍රමයෙන් අඩු වී රෙස්ටිං සංඛ්‍යාතයට පැමිණේ.

එහෙත් සංඥාව තිරස් අක්ෂයෙන් නතරවන්නේ නැත. එය යටි දිශාව (එනම් ඍණ දිශාව) ඔස්සේ නැවත උපරිම විස්තාර අගයක් කරා ගමන් කරයි. මෙහිදී යටි පැත්තට හෙවත් ඍණ පැත්තට සංඥා විස්තාර අගය වැඩි වන නිසා, එය විස්තාර අගයේ අඩු වීමක් ලෙස සැලකිය යුතුයි (ඍණ අගයන් යනු 0 ට වඩා අඩු අගයන්නෙ). ඒ අනුව ඍණ පැත්තට සංඥා විස්තාරය වැඩි වීම වාහක සංඛ්‍යාතය අඩු වීමක් ලෙසයි දක්වන්නෙ. එවිට ඉහත විස්තරය අනුවම සෑම මිලිවෝල්ට් 1කටම හර්ට්ස් 10 බැඟින් අඩු කරගෙන යා යුතුය.

ඒ අනුව, සංඥා තරංගය ශූන්‍ය අගයේ සිට (ඍන හෙවත් පහල පැත්තට යන විට හෙවත්) අගය මිලිවෝල්ට් 1කින් අඩු වන විට, වාහක සංඛ්‍යාතයද හර්ට්ස් 10කින් අඩු වේ. එවිට, වාහක තරංග සංඛ්‍යාතය 100,000,000-10 = 99,999,990 හර්ට්ස් වේවි.

එලෙස (ඍන පැත්තෙන් උපරිම විස්තාර අගයට යන විට හෙවත්) සංඥාව අවම අගයට යන විට, එතැන වෝල්ටියතාව -1000mV නිසා, හර්ට්ස් 10x1000 = 10,000 කින් වාහක සංඛ්‍යාතය අඩු විය යුතුය. එවිට වාහක සංඛ්‍යාතය 100,000,000-10,000 = 99,990,000 හර්ට්ස් හෙවත් මෙගාහර්ට්ස් 99.99වේ.

ඉහත උදාහරණය අනුව, සංඥා අගය වෝල්ට් -1ක අවම අගයේ සිට වෝල්ට් 1ක උපරිම අගය දක්වා විචලනය වන විට, වාහකය සංඛ්‍යාතය හර්ට්ස් 99,990,000 සිට හර්ට්ස් 100,010,000 දක්වා විචලනය විය. වාහකයේ රෙස්ටිං සංඛ්‍යාතයේ සිට ඉහලටත් (සංඛ්‍යාතය වැඩි වන ලෙසට) පහලටත් (සංඛ්‍යාතය අඩු වන ලෙසට) වාහක සංඛ්‍යාතය අපගමනය (deviate) වී තිබෙන බව පෙනෙනවා. මෙලෙස සංඥාවක් සංඛ්‍යාත මූර්ජනය කරන විට, සංඥාවේ වෝල්ටියතාව අනුව වාහකයේ සංඛ්‍යාතයේ සිදුවන වැඩිම අපගමනය උපරිම සංඛ්‍යාත අපගමනය (maximum frequency deviation) ලෙස හැඳින්වේ. එය f_d හෝ δ ලෙස සංඛේතවත් කෙරේ. ඒ අනුව ඉහත උදාහරණයේ සංඛ්‍යාත අපගමනය 10,000Hz හෙවත් 10kHz වේ. ඉහල හා පහල යන දිශා දෙක ඔස්සේම මෙම අපගමනය වෙන වෙනම සිදු වන බැවින් ±10kHz වැනි ආකාරයට ± යන සංඛේතයද සමග අපගමනය ලිවිය හැකිය.

තවද, වාහක සංඛ්‍යාතය ඉහත අයුරින් අපගමනය වූයේ බුද්ධි සංඥාවේ විස්තාර අගයට අනුවයි. වාහකයට බුද්ධි සංඥාවේ සංඛ්‍යාතයේ බලපෑමක් තිබේද?

බුද්ධි සංඥාවේ සංඛ්‍යාතය ඉහත හඳුන්වා දුන් සංඛ්‍යාත අපගමනයට ඍජු බලපෑමක් ඇති කරන්නේ නැති බව නම් පැහැදිලියි. එහෙත් එම සංඛ්‍යාත අපගමනය හැරුණහම බුද්ධි සංඥාවේ සංඛ්‍යාතය නිසාද අවසාන විස්තාර මූර්ජිත සංඥා සංඛ්‍යාතයට යම් බලපෑමක් ඇති වේ.

ඒ කියන්නේ මූර්ජිත සංඥා සංඛ්‍යාතය විචලනය කරන සාධක දෙකක් ඇත – බුද්ධි සංඥා විස්තාර අගය හා බුද්ධි සංඥා සංඛ්‍යාතය. කෙසේ වෙතත්, එම සාධක දෙකෙහිම බලපෑම නිසා අවසාන මූර්ජිත සංඥාව සකස් වන ආකාරය එකවර හෝ පහසුවෙන් අවබෝධ කර ගැනීමට හෝ සිතින් මවා ගැනීමට නම් අපහසුතාවක් ඇත (විස්තාර මූර්ජනය නම් එවැනි අපහසුතාවකින් තොරව පහසුවෙන් තේරුම් ගත හැකි බව මීට පෙර අප දුටුවා). එනිසා එය යම් මට්ටමකින් හෝ තේරුම් ගැනීමට හා ගණනය කිරීම් සඳහා සුපුරුදු ලෙසම ගණිත සූත්‍ර අපගේ උදව්වට පැමිණේ.

ගණිත සූත්‍ර හඳුන්වා දෙන්නට පෙර, සංඛ්‍යාත මූර්ජනයේදී සංඥා විස්තාර අගය හා සංඥා සංඛ්‍යාතය යන සාධක දෙකම එක්ව අවසාන මූර්ජිත සංඥාව සකස් වන අයුරු අපට යම් දුරකට තේරුම්ගත හැකිය. ඒ ගැන දැන් විමසමු.

ඉහත උදාහරණයේදී සංඥා විස්තාරයේ සෑම මිලිවෝල්ට් එකක් සඳහාම හර්ට්ස් 10ක් බැගින් වෙන් කළා නේද? උදාහරණයක් ලෙස, සංඥාව දැන් තිබෙන්නේ මිලිවෝල්ට් 20 නම්, එය කාලයත් සමග මිලිවෝල්ට් 21 දක්වා ඉහල නැංගේ නම්, එවිට වාහක සංඛ්‍යාතය දැන් තිබෙන සංඛ්‍යාතයට වඩා හර්ට්ස් 10කින් වැඩිවිය යුතුයිනෙ. බැලූබැල්මට කිසිදු ගැටලුවක් නැතැයි පෙනුනත් එතැන යම් සංකීර්ණතාවක් ඇත.

මිලිවෝල්ට් 20 සිට 21ට එකවර සංඥාව ගමන් කළේ නැහැනෙ. කාලයත් සමග සන්තතිකව හෙවත් සුමට ආකාරයෙනුයි එම වැඩිවීම සිදු වන්නේ. ඒ කියන්නේ මිලිවෝල්ට් 20ත් 21ත් අතර අපට කුඩා වෝල්ටියතා මට්ටම් අනන්ත ගණනක් දැක්විය හැකියි (ඇනලොග් තරංගයක ස්වභාවය එය බව මීට පෙර අප ඉගෙන ඇත). මෙන්න මෙම ඇනලොග් ස්වභාවය තමයි සංකීර්ණතාව ඇති කරන්නේ. මිලිවෝල්ට් 1ක වෝල්ටියතා පරාසයක් සඳහා හර්ට්ස් 10ක් වෙන් කර තිබෙන නිසා, මිලිවෝල්ට් 0.1ක් හෙවත් මයික්‍රොවෝල්ට් 100ක් සඳහා හර්ට්ස් 1ක් අවශ්‍ය වේ. එවිට, මයික්‍රොවෝල්ට් 10ක් සඳහා අවශ්‍ය වන හර්ට්ස් ගණන 0.1ක් නේද? එලෙසම මයික්‍රොවෝල්ට් 1ක් සඳහා හර්ට්ස් 0.01ක් ද, මයික්‍රොවෝල්ට් 0.1ක් සඳහා හර්ට්ස් 0.001ක්ද ආදී ලෙස හර්ට්ස් අගයන් ගණනය කළ හැකියිනෙ (මෙලෙස නැවත නැවත කුඩා පරිමාණ මට්ටම් දක්වා යෑමේ ඉවරයක් නැත).

මෙවිට ඉහත ආකාරයට මිලිවෝල්ට් 20 සිට 21 දක්වා සතතයෙන් (continuously) සංඥා අගය වැඩි වන විට, වාහකයේ සංඛ්‍යාතයද සතතයෙන් වැඩි වේ. එය ඔබ මතුපිටින් සිතූ ලෙස හර්ට්ස් 10න් 10 හෝ හර්ට්ස් 1න් 1 හෝ ලෙස නොවෙයි වැඩි වන්නේ. සංඥාවේ වෝල්ටියතාව අනන්ත මට්ටම් ගණනකට බෙදිය හැකිවා මෙන්ම, වාහකයේ සංඛ්‍යාතයද මට්ටම් අනන්ත ගණනකින් දැක්විය හැකියි. උදාහරණයක් ලෙස, මිලිවෝල්ට් 20දී වාහක සංඛ්‍යාතය හර්ට්ස් 100,000,200 නම්, මිලිවෝල්ට් 21දී වාහක සංඛ්‍යාතය හර්ට්ස් 100,000,210 වේ. මෙම හර්ට්ස් අගයන් දෙක අතර, අනන්ත ගණනක් වූ සංඛ්‍යාත මට්ටම් පවතීවි හර්ට්ස් 100,000,000.0001, 100,000,000.0002, 100,000,000.0003 ආදී ලෙස (මා දශමස්ථාන 4න් 4ට දැක්වුවත්, ඔබට අවශ්‍ය නම් දශමස්ථාන ලක්ෂ ගණනක් වුවද ගත හැකියි; ඒකනේ මට්ටම් අනන්ත ගණනක් දැක්විය හැකියි කියා කිව්වෙ). සංඥා විස්තාරය මෙන්ම වාහක සංඛ්‍යාතයද ඇනලොග් බව අමුතුවෙන් කිව යුතු නැහැනෙ.

මෙයින් හැඟවෙන්නේ සංඛ්‍යාත මූර්ජිත අවසාන සංඥාවේ තරංගයට නිශ්චිත නියත පිරිසිදු සයිනාකාර තරංග හැඩයක් නැත යන්නයි. ඒ වෙනුවට කාලයත් සමග තරංගය ඇදෙන (දික් වෙන) හෝ සංකෝචනය වන (කෙටි වෙන) ආකාරයෙනුයි අවසාන සංඥා තරංගය පවතින්නේ (එනම්, විකෘති වූ තරංග හැඩයක් ඇති වේ). ඒ කියන්නේ ෆූරියර් න්‍යාය අනුව (අක්‍රමවත්) තරංගය සංඛ්‍යාතය විවිධ වූ සයිනාකාර තරංග ගොන්නකින් (අනන්ත ගණනකින්) සෑදී තිබේ යැයි සිතිය හැකිය.

ඉහත විස්තරයේ කියූ ආකාරයට සංඛ්‍යාතයේ සිදු වන සන්තතික විචලනය නිසා, ඉන් ගම්‍ය වන්නේ සංඥාවට අනුරූපව වාහක සංඛ්‍යාතය විචලනය වන විට, ඒ සඳහා සංඛ්‍යාතයන් අනන්ත ගණනක් අවශ්‍ය කරන බවයි. ඔව්. සංඛ්‍යාත මූර්ජනයේදී එක් සංඥාවක් විසුරුවාලීමට අවශ්‍ය සංඛ්‍යාත පරාසය අනන්තයකි (එනම් බෑන්ඩ්විත් එක අනන්තයකි). ඒ කියන්නේ සම්පූර්ණ රේඩියෝ සංඛ්‍යාත පරාසයම එක් සංඥාවක් විසුරුවා ලීමට අවශ්‍ය කරන බවයි. සෛද්ධාන්තිකව තත්වය එසේ වුවද, ප්‍රායෝගික තත්වය ඊට වඩා බොහෝ යහපත්ය. මොහොතකින් සංඛ්‍යාත මූර්ජනයේදී සංඥාවක් විසුරුවාලීම සඳහා සත්‍ය වශයෙන්ම අවශ්‍ය කරන බෑන්ඩ්විත් අගය (අනන්තයට වඩා බෙහෙවින්) කුඩා බවත්, එය ගණනය කරන අයුරුත් කියා දෙන්නම්.

සංඛ්‍යාත මූර්ජනය ගැන ගණනය කිරීම්වලදී නිතර හමුවන රාශියක් තමයි Modulation Index of Frequency Modulation (FM Modulation Index) කියන්නේ. එය m_f ලෙස සංඛේතවත් කෙරේ. මෙය විස්තාර මූර්ජනයේදී හමුවූ ඒඑම් මොඩ්‍යුලේෂන් ඉන්ඩෙක්ස් රාශියට වඩා වෙනස් බව මතක තබා ගන්න. එෆ්එම් මොඩ්‍යුලේෂන් ඉන්ඩෙක්ස් රාශිය පහත ආකාරයටයි සොයා ගන්නේ.

FM modulation Index = (frequency deviation) / (signal frequency)             m_f = f_d / f_s

උදාහරණයක් ලෙස, සංඛ්‍යාත මූර්ජනය කරන පරිපථයක් නිර්මාණය කර තිබෙන්නේ උපරිම සංඛ්‍යාත අපගමනය ±12kHz, හා සංඥාවේ පවතින උපරිම සංඛ්‍යාතය 3kHz වන ලෙස නම්, එවිට m_f අගය වන්නේ 12000Hz/3000Hz (= 12kHz/3kHz) = 4 වේ.

දැන් අපි එෆ්එම් මූර්ජනය ගණිතමය ආකාරයෙන් විශ්ලේෂනය කරමු. සුපුරුදු ලෙසම වාහක තරංගය හා සංඥා තරංගය (සංඥාව සයිනාකාර යැයි උපකල්පනය කර ඇත) පහත සූත්‍ර දෙකෙන් දැක්විය හැකියිනෙ.

v_carrier = V_C sin(2πf_Ct)

v_signal = V_S sin(2πf_St)

ඉහත V_signal නම් බුද්ධි සංඥාවට අනුරූපවනෙ V_carrier තරංගය සංඛ්‍යාත මූර්ජනය කළ යුත්තේ. ඒ කියන්නේ වාහක තරංගයේ සංඛ්‍යාතය සහිත කොටසටයි සංඥා වෝල්ටියතාවේ ඍජු බලපෑම (විචලනය කිරීම) පවතින්නේ. එනිසා එම තත්වය පහත ආකාරයට සූත්‍රයකට නැංවිය හැකියි.

v_FM = V_Csin[2πf_Ct + m_fsin(2πf_st)]

ඉහත සූත්‍රය විසඳීමට (සරල කිරීමට) තරමක ගණිත හැකියාවක් තිබිය යුතුය. ඉතිං එම සූත්‍රය විසඳිය හැක්කේ කෙසේදැයි ගණිතඥයකුගෙන් ඇසූ විට, ඔහු කියාවි Bessel function නම් ක්‍රමවේදය ඊට යෙදිය යුතු බව. ඉතිං ඔහුටම එය අප වෙනුවෙන් විසඳා දෙන ලෙස කියූ විට, එහි විසඳුම පහත ආකාරයට ලබා ගත හැකියි (සාමාන්‍ය අප ගණිතඥයන් නොවෙයිනෙ; එහෙත් බෙසෙල් ශ්‍රිත ගැන අවශ්‍ය කෙනෙකුට වැඩිදුරට සොයා ඉගෙන ගත හැකියි).

v_FM = V_c [ J₀(sinω_ct) +

                  J₁{sin(ω_c+ω_m)t – sin(ω_c-ω_m)t} +

                  J₂{sin(ω_c+2ω_m)t – sin(ω_c-2ω_m)t} +

                  J₃{sin(ω_c+3ω_m)t – sin(ω_c-3ω_m)t} +

                  J₄{sin(ω_c+4ω_m)t – sin(ω_c-4ω_m)t} +

                  J₅{sin(ω_c+5ω_m)t – sin(ω_c-5ω_m)t} +

                  J₆{sin(ω_c+6ω_m)t – sin(ω_c-6ω_m)t} +

                  …]

සටහන

තරංගයක සංඛ්‍යාතය දෙයාකාරයකින් අපට ගණිත සූත්‍ර තුල දක්නට ලැබේ. එක් ආකාරයක් නම්, හර්ට්ස්වලින් දක්වන සංඛ්‍යාතය (f) වේ. එය සාමාන්‍ය සංඛ්‍යාතය වේ. දෙවැනි ආකාරය නම්, තත්පරයට රේඩියන් (rad/s) නම් ඒකකයෙන් දක්වන කෝණික සංඛ්‍යාතය (ω) වේ. මෙම ක්‍රම දෙකෙන් එක් ක්‍රමයකින් අගය දී ඇති විට, අනෙක් ක්‍රමයෙන් අගය සෙවිය හැකියි ω=2πf යන සරල සූත්‍රය අනුව. උදාහරණයක් ලෙස, යම් තරංගයක සාමාන්‍ය සංඛ්‍යාතය හර්ට්ස් 100 නම්, එහි කෝණික සංඛ්‍යාතය වන්නේ ω = 2πf = 2 x 3.14 x 100 = 628 rads^-1 වේ.

ඉහත සූත්‍රයේ අග … ලෙස දක්වා තිබෙන නිසා, ඉන් හැඟවෙන්නේ තවත් පද අනන්ත ගණනක් තිබෙන බවයි. එම පද සියල්ලම යම් රටාවකට පිහිටා ඇති බව පේනවා නේද? එනිසා අවශ්‍ය නම්, ඔබට හැකියි තවත් පද ඕනෑ තරමක් එහි ලියා දක්වන්නට. කොටු වරහන තුල ඇති සියලු පදවල එකතුව වාහක තරංගයේ උපරිම විස්තාර අගයෙන් (V_C) ගුණ කෙරේ.

තවද, ඉහත සූත්‍ර තුල මා සංඛ්‍යාතය දක්වා තිබෙන්නේ කෝණික සංඛ්‍යාත ක්‍රමයටයි. අවශ්‍ය නම් සාමාන්‍ය සංඛ්‍යාත නිරූපණය ක්‍රමයෙන්ද එම පද ලිවිය හැකියි (උදාහරණයක් ලෙස, + J₁{sin(ω_c+ω_m)t – sin(ω_c-ω_m)t} + වැනි පද + J₁{sin(2πf_c+2πf_m)t – sin(2πf_c-2πf_m)t} + ලෙස හෝ + J₁{sin(f_c+f_m)2πt – sin(f_c-f_m)2πt} + ලෙස ලිවිය හැකියි). එහෙත් කෝණික සංඛ්‍යාත යොදා ගන්නා විට ලිවිය යුතු අමතර කොටස් (2π) අඩු වී පහසු වන නිසා, බොහෝවිට කෝණික සංඛ්‍යාත තමයි මෙම සූත්‍රයේ යොදන්නේ.

එක් එක් සඟල වරහන තුල ඇති ප්‍රකාශය බලන්න. එහි සයින් ශ්‍රිත දෙකක් පෙනේ. එක් සයින් ප්‍රකාශයක සංඛ්‍යාත දෙකක් එකතු කරද, අනෙක් සයින් ශ්‍රිතයේ එම සංඛ්‍යාත දෙකෙහි අන්තරයක්ද ලෙසයි පවතින්නේ. තවද, වාහක සංඛ්‍යාතය (ω_c) නියතව පවතී ඒ සෑම ප්‍රකාශයක් තුලම. එහෙත් සංඥා සංඛ්‍යාතය වාහක සංඛ්‍යාතයට එකතු කරන විට හා වාහක සංඛ්‍යාතයෙන් සංඥා සංඛ්‍යාතය අඩු කරන විට, සංඥා සංඛ්‍යාතයේ 1,2,3 ආදී ගුණාකාරයි පවතින්නේ (ω_c+ω_m හා ω_c-ω_m , ω_c+2ω_m හා ω_c-2ω_m , ω_c+3ω_m හා ω_c-3ω_m , ω_c+4ω_m හා ω_c-4ω_m ) .

තවද, සෑම සඟල වරහයනක්ම J₀, J₁, J₂ ආදී යම් සංගුණක පදයකින් ගුණ වී තිබේ. මෙම සංගුණක පදවල අගයන් තවම අප දන්නේ නැත. එම සෑම පදයක්ම සෙවීමට පහත ආකාරයේ තවත් සූත්‍රයක් තිබේ (පෙනෙන තරම් මෙම සූත්‍ර කිසිවක් අමාරු නැති අතර, සාමාන්‍ය කැල්ක්‍යුලේටරයකින් වුවද මේවා විසඳිය හැකිය). මෙම සූත්‍රයේද පවතින පොදු රටාව තේරුම් ගන්න. මෙහිද … ලෙස දක්වා තිබෙන්නේ තවත් පද ලිවිය හැකි බවයි. එහෙත් එතරම් දුරට නිවැරදි අගයන් අපට අවශ්‍ය නැති අතර, පෙන්වා දී ඇති පද ගණන වුවද සුලු කිරීම හොඳටම ප්‍රමාණවත්ය.

ඉහත සංගුණක පද සෙවීමේ සූත්‍රයට විචල්‍ය පද 2ක් ඇතුලත් වේ. එකක් නම්, එෆ්එම් මොඩ්‍යුලේටර් පරිපථය නිර්මාණය කරන විට අප විසින්ම තීරණය කරන මොඩ්‍යුලේෂන් ඉන්ඩෙක්ස් අගයයි (m_f). අනෙක් විචල්‍යය වන්නේ සෙවීමට අවශ්‍ය සංගුණක පදය කුමක්ද (n) යන්නයි. ඉහත සූත්‍රය යොදාගෙන ගණනය කිරීම් කිහිපයක් කරමු. උදාහරණය සඳහා මා m_f=2 ලෙස ගන්නවා. එවිට පළමු සංගුණක පද 8 සඳහා (J₀ සිට J₇ දක්වා) ලැබෙන අගයන් ගණනය කරමු.

පළමු පදය (J₀) සොයමු.

සටහන

ඉහත ගණනය කිරීමේදී එකතු කිරීම, අඩු කිරීම, ගුණ කිරීම, බෙදීම, බලයකට නැංවීම (exponentiation), හා ක්‍රමාරෝපිතය (factorial) නම් සරල ගණිත කර්ම පමණි තිබුණේ. ඉහත ගණනය කිරීම්වල හමු වූ විශේෂිත අවස්ථා කිහිපයක් කෙටියෙන් පහත දක්වනවා.

ශූන්‍ය නොවන ඕනෑම ධන හෝ ඍන අගයක් 0 වැනි බලයට නංවන විට හැමවිටම පිළිතුර ලෙස ලැබෙන්නේ 1 වේ (x⁰ =1).

ක්‍රමාරෝපිතය සංඛේතවත් කරන්නේ යම් පූර්ණ සංඛ්‍යාවකට (integer හෙවත් whole number) පසුව ! යන සංඛේතය යෙදීමෙනි. එවිට, 1 සිට එම අගය දක්වා වූ සියලු පූර්ණ සංඛ්‍යා එකිනෙකට ගුණ කළ යුතුය. උදාහරණයක් ලෙස, 4! = 1 x 2 x 3 x 4 වන අතර, 7! = 1 x 2 x 3 x 4 x 5 x 6 x 7 වේ.

අර්ථ දැක්වීමෙන්ම සම්මතය ලෙස 0 හි ක්‍රමාරෝපිතය 1 වේ (0! = 1). එලෙසම 1 හි ක්‍රමාරෝපිතය ඉතිං කොහොමත් 1 වේ (1! = 1).

අප ඉහත සෙව්වේ පළමු සංගුණක පදයේ අගයයි. මෙලෙසම දෙවැනි (J₁), තෙවැනි (J₂) ආදී පදවල අගයන්ද සෙවිය හැකියිනෙ. එවිට එම අගයන් පහත ආකාරයට ලැබේවි. බලන්න එම සංගුණක පද ඉහලට යන විට එහි අගයන් සීඝ්‍රයෙන් පහල යයි. උදාහරණය සඳහා ලැබුණු අගයන් පහත වගුවේ දැක්වෙන අතර, එහි පැහැදිලිවම පෙනෙනවා එම අගයන් සීඝ්‍රයෙන් පහල යන හැටි. අන්තිම පද කිහිපයේ අගය කොතරම් අඩුද යත්, දශමස්ථාන12කට දක්වා තිබියදීත් එම අගයන් කුඩා වැඩි නිසා ශූන්‍ය ලෙස පෙනේ.

සංගුණක පදය	අගය
J0	0.222222222222
J1	0.576427469136
J2	0.044098668981
J3	0.000055962431
J4	0.000000000600
J5	0.000000000000
J6	0.000000000000
J7	0.000000000000

ඉහත අප උදාහරණයට ගත්තේ m_f=2 වන අවස්ථාවයි. මෙම මොඩ්‍යුලේෂන් ඉන්ඩෙක්ස් අගය වෙනස් කරන විට, ඉහත සංගුණක පද සියල්ලම එකිනෙකට වෙනස් වේ. විවිධ ඉන්ඩෙක්ස් අගයන් සඳහා වන සංගුණක පදවල අගයන් (පළමු පද 14 සඳහා) පහත වගුවේ ඇත.

ඉහත වගු ආකාරයෙන් දක්වන දත්තයම ප්‍රස්ථාරයක් ආකාරයෙන්ද දැක්විය හැකිය. එවිට පහත ආකාරයේ ප්‍රස්ථාරයක් ලැබේවි. ඉහත වගුවේ දැක්වෙන සියලු අගයන් මෙම ප්‍රස්ථාරය තුලින් සොයා බලන්න (සරල අභ්‍යාසයක් විදියට එය කරන්න).

ඉතිං, බෙසල් ක්‍රමයට අවසන් මූර්ජිත සංඥාව නිරූපණය කරන ගණිත සමීකරණයේ විසඳුම ඒ අනුව ඉහත සූත්‍ර දෙකකිනුයි දක්වන්නේ. මෙම සූත්‍ර දෙක සමහරෙකුට එකවර බය හිතෙන තරම් වුවත්, ටික වෙලාවක් ඒ සමග වැඩ කරන විට, සරල බව දැනේවි. බය හිතෙන තරම් වුවත්, සරල ලෙස දැනුනත්, එම සූත්‍ර දෙකෙහි ප්‍රතිපල රූපයකට නැඟූ විට නම්, ඉතාම වටිනා කරුණු කිහිපයක් ඔබට සංඛ්‍යාත මූර්ජනය ගැන දැනගත හැකි වේ.

පළමුව අපි බලමු ඉන්ඩෙක්ස් අගය 0 වන විට සිදු වන දේ. මෙවිට, ඉහත සූත්‍ර සඳහා m_f=0 ලෙස ආදේශ කරමින් ගණනය කිරීම් කළ විට, ඔබට පෙනේවි, J₀ සංගුණකය හැර සෙසු සියලුම සංගුණක පද ශූන්‍ය වන බව. J₀ සංගුණකයේ අගය 1 ලෙස ලැබේවි (අවශ්‍ය නම්, සංගුණක අගය සොයන සූත්‍රය සුලු කර බලන්න මා මේ කියූ දේවල් එලෙස සිදු වේද කියා). අනෙක් සංගුණක පද සියල්ලම 0 නිසා,

v_FM = V_c [ J₀(sinω_ct) + J₁{sin(ω_c+ω_m)t – sin(ω_c-ω_m)t} + J₂{sin(ω_c+2ω_m)t – sin(ω_c-2ω_m)t} + J₃{sin(ω_c+3ω_m)t – sin(ω_c-3ω_m)t} + J₄{sin(ω_c+4ω_m)t – sin(ω_c-4ω_m)t} + J₅{sin(ω_c+5ω_m)t – sin(ω_c-5ω_m)t} + J₆{sin(ω_c+6ω_m)t – sin(ω_c-6ω_m)t} + …]

යන සූත්‍රයේ J₁, J₂, J₃ ආදී තැන් සියල්ලම 0 වේ. එවිට

v_FM = V_c [ 1(sinω_ct) + 0{sin(ω_c+ω_m)t – sin(ω_c-ω_m)t} + 0{sin(ω_c+2ω_m)t – sin(ω_c-2ω_m)t} + 0{sin(ω_c+3ω_m)t – sin(ω_c-3ω_m)t} + 0{sin(ω_c+4ω_m)t – sin(ω_c-4ω_m)t} + 0{sin(ω_c+5ω_m)t – sin(ω_c-5ω_m)t} + 0{sin(ω_c+6ω_m)t – sin(ω_c-6ω_m)t} + …] = V_c [ (sinω_ct) + 0 + 0 + 0 + 0 + 0 + 0] = V_c(sinω_ct)

වේ. ඒ කියන්නේ ඉන්ඩෙක්ස් අගය 0 විට, අවසාන මූර්ජිත සංඥාවේ පවතින්නේ වාහක තරංගය පමණි. ඉතිං එය නිවැරදියිනෙ. මොඩ්‍යුලේෂන් ඉන්ඩෙක්ස් අගය 0 යැයි කියන්නේ එතැන කිසිදු බුද්ධි සංඥාවක් නැතැයි කියානෙ. රූප සටහනක් ලෙස එය පහත ආකාරයට ඇඳිය හැකිය.

දැන් අපි බලමු m_f=1 වන විට තත්වය කෙබඳුද කියා. එවිට මීට පෙර සංගුණක පද දක්වපු වගුවෙන් m_f=1 අවස්ථාවට අදාල J අගයන් v_FM සූත්‍රයට ආදේශ කරමු.

V_FM = V_c [ 0.22(sinω_ct) + 0.58{sin(ω_c+ω_m)t – sin(ω_c-ω_m)t} + 0.35{sin(ω_c+2ω_m)t – sin(ω_c-2ω_m)t} + 0.13{sin(ω_c+3ω_m)t – sin(ω_c-3ω_m)t} + 0.03{sin(ω_c+4ω_m)t – sin(ω_c-4ω_m)t} + 0{sin(ω_c+5ω_m)t – sin(ω_c-5ω_m)t}] = V_c [ 0.22(sinω_ct) + 0.58{sin(ω_c+ω_m)t – sin(ω_c-ω_m)t} + 0.35{sin(ω_c+2ω_m)t – sin(ω_c-2ω_m)t} + 0.13{sin(ω_c+3ω_m)t – sin(ω_c-3ω_m)t} + 0.03{sin(ω_c+4ω_m)t – sin(ω_c-4ω_m)t}]

ලෙස එය සකස් වේ. දැන් එය රූපයට නැඟූ විට පහත ආකාරයට දිස් වේ.

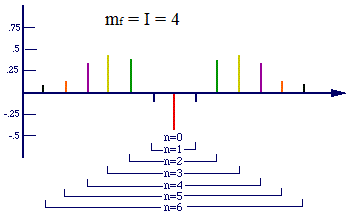
පහත දැක්වෙන්නේ m_f = 4 වන අවස්ථාවයි.

m_f=0.25 අවස්ථාවත් එලෙසම බලමු. ඉහත J අගයන් දක්වපු වගුව බලන විට ඔබට පෙනෙනවා නේද J₀, J₁ යන සංගුණක හැර වෙනත් සංගුණක පද එහි නැති බව (එනම් අනෙක් සෙසු සංගුණක පදවල අගය 0 වේ). එය පහත රූපයෙන් නිරූපනය කෙරේ.

හරි… දැන් බලමු ඉහත සූත්‍ර දෙක ආශ්‍රයෙන් ලැබුණු මෙම රූපවල වැදගත්කම කුමක්ද කියා. ඇත්තටම මෙම රූපවලින් දැක්වෙන්නේ සංඛ්‍යාත මූර්ජනය නිසා ජනිත වන අවසාන මූර්ජිත සංඥාවයි.

එහි J₀ සංගුණකය නිරූපණය කරන්නේ වාහක තරංගයයි. මෙම රූප බලන විට, J₀ මැදි කොට ගෙන දෙපසින් සමාන දුරවලින් J₁ සහිත පද පිහිටයි.

වාහකයට වම්පසින් (සංඛ්‍යාතය අඩු පැත්තෙන්) පිහිටන්නේ J₁{sin(ω_c+ω_m)t – sin(ω_c-ω_m)t} යන කොටසෙහි අඩංගු sin(ω_c-ω_m)t යන පදයයි. වාහකයට දකුණින් (සංඛ්‍යාතය වැඩි පැත්තෙන්) පිහිටන්නේ sin(ω_c+ω_m)t යන පදයයි. සෑම J සංගුණකයකටම පසුව මෙලෙස සයින් කොටස් දෙකක් තිබීම රූපයේ දිස්වන්නේ එලෙසයි. ඉතිං මොක්කද J₁ න් නිරූපණය වන්නේ? J₀ පදයෙන් නම් වාහකය නිරූපණය වන බව දුටුවනෙ. J₁ සහිත සයින් කොටස් බලන්න. එහි (ω_c+ω_m) හා (ω_c-ω_m) ලෙසනෙ තිබෙන්නේ. ඒ කියන්නේ එකක් වාහක සංඛ්‍යාතයට සංඥා සංඛ්‍යාතය එකතු වී තිබෙන අවස්ථාවයි (ω_c+ω_m); අනෙක වාහක සංඛ්‍යාතයෙන් සංඥා සංඛ්‍යාතය අඩු කර තිබෙන අවස්ථාවයි (ω_c-ω_m). ඒ කියන්නේ J₁ මඟින් ලැබී තිබෙන්නේ මූර්ජනය නිසා ඇතිවූ සයිඩ්බෑන්ඩ් දෙකයි. විස්තාර මූර්ජනයේදි මෙන්ම වාහකය දෙපස සයිඩ්බෑන්ඩ් 2ක් පවතිනවා.

එතකොට J₂, J₃ ආදී ලෙස තිබෙන පද මොනවාද? ඒවායේ සයින් ශ්‍රිත තුල තිබෙන (ω_c+2ω_m), (ω_c+3ω_m) කොටස් දකින විට ඉන් ගම්‍ය වන දේ ඔබට දැන් වැටහිය යුතුය. ඔව්, J₂ වලින් නියෝජනය වන්නේ වාහක සංඛ්‍යාතයට සංඥා සංඛ්‍යාතයේ දෙගුණය එකතු වී ඇති (ω_c+2ω_m) හා වාහක සංඛ්‍යාතයෙන් සංඥා සංඛ්‍යාතයේ දෙගුණයක් අඩු වී ඇති (ω_c-2ω_m) අවස්ථා දෙකයි. එලෙසම J₃ යනු සංඥා තරංග සංඛ්‍යාතයේ තුන්ගුණය සහිත අවස්ථාවයි. මෙම පද රූපයේ පිහිටන්නේ වාහකයට තවත් ඈතිනි. මෙලෙස අනෙක් J පද ගැනත් සිතන්න.

ඉතිං ඉහත විස්තරය අනුව පෙනෙනවා සංඛ්‍යාත මූර්ජනයේදී වාහක දෙපස එක් සයිඩ්බෑන්ඩ් යුගලක් වෙනුවට සයිඩ්බෑන්ඩ් යුගලවල් කිහිපයක්ම පවතින බව. න්‍යායාත්මකව මෙලෙස සයිඩ්බෑන්ඩ් යුගලවල් අනන්ත ගණනක් ලැබේ. ඊට හේතුව J පද අනන්ත ගණනක් පැවතීමයි. ඒකයි මුලදී මා පැවසුවේ එෆ්එම් ක්‍රමයේදී යම් සංඥාවක් විසුරුවාලීම සඳහා අවශ්‍ය වන සංඛ්‍යාත පරාසය අනන්තයක් බව. එහෙත් ප්‍රායෝගික තත්වය එසේ නොවන බවද මා එහි සඳහන් කළා. ඊට හේතුව ඉහල J පදවල අගය ඉතාම කුඩා වීමයි. එනම් එම ඉහල J පද සහිත සයිඩ්බෑන්ඩ්වල ශක්තිය ශූන්‍යයට ඉතා ආසන්නය. එනිසා එම කුඩා ජවයන් සහිත පද නොසලකා හැරිය හැකිය. එනිසා අවසානයේ, සයිඩ්බෑන්ඩ් කිහිපයක් පමණයි ඉතිරි වන්නේ. ඒ කියන්නේ ප්‍රායෝගික භාවිතාව තුලදී අනන්ත සංඛ්‍යාත පරාසයක් අවශ්‍ය කරන්නේ නැති බවයි.

වචනයෙන් මා කිව්වත් ඉහල සංගුණක පද නොසලකා හරිනවා කියා, එය ඇත්තටම තීරණය කරන විදියක් තිබෙනවා. එක් එක් J පදවලට යම් යම් අගයන් තිබුණනෙ. මෙම අගයන්ගෙන් නිරූපණය කරන්නේ මොඩ්‍යුලේටර් පරිපථයට සපයපු විදුලි ජවයෙන් කොතරම් ප්‍රමාණයක් එම J පදයට හිමි වෙනවාද යන්න ගැන හිඟියකි. ඒ අනුව දැන් නැවත ඉහත රූප පරික්ෂා කර බලන්න ඒ ඒ සයිඩ්බෑන්ඩ් යුගලවලට ලැබෙන ජව අනුපාතයන් ගැන හිඟියක් ලබා ගැනීම සඳහා. සමහර J අගයන් ඍන අගයන් ලෙසද පැවතිය හැකියි. එහි අර්ථය වාහක තරංගයට සාපේක්ෂව අංශක 180 කලා වෙනසක් පවතින බවයි (ඉහතදී mf = 4 අවස්ථාවට අදාල රූපය බලන්න; එහි වාහකය ඍන අගයකි).

එහෙත් 1%කට වඩා අඩු J අගයන් (එනම් J අගය 0.01ට වඩා අඩු විට) අප නොසලකා හරිනවා. ඉහත J අගය වගුව නැවත බැලුවොත් පෙනේවි 0.01ට වඩා අඩු අගයන් සහිත J පද එහි සටහන් නොකර ඇති බව.

කෙසේ වෙතත්, සංඛ්‍යාත මූර්ජනයේදී විස්තාර මූර්ජනයට වඩා වැඩි සංඛ්‍යාත පරාසයක් (බෑන්ඩ්විත් එකක්) අවශ්‍ය කෙරෙනවා මොකද ඉහත උදාහරණයට ගත් අවස්ථාවල පෙන්නුම් කළ පරිදි සයිඩ්බෑන්ඩ් කිහිපයක්ම මූර්ජිත සංඥාවේ පවතිනවා.

එහෙත් විශේෂිත අවස්ථාවක් තිබෙනවා එක් සයිඩ්බෑන්ඩ් යුගලක් පමණක් පවතින. එම අවස්ථාව එළඹෙන්නේ m_f=0.25 වන විටය. මෙම අවස්ථාවේදී එෆ්එම් සම්ප්‍රේෂනය සඳහා වැය වන්නේ ඒඑම් සම්ප්‍රේෂනය සඳහා වැය වූ තරමේ කුඩා බෑන්ඩ්විත් එකකි. මෙම විශේෂිත අවස්ථාව Narrowband FM (NBFM) ලෙස හැඳින්වෙනවා. ඇත්තටම මෙම m_f අගය 0.2 සිට 0.25 අතර අගයක ප්‍රායෝගිකව පැවතිය හැකිය. එහෙත් අර්ථ දැක්වීම අනුව නම්, නැරෝබෑන්ඩ් එෆ්එම් යනු m_f අගය π/2 හෙවත් 1.57 ට අඩුවෙන් පවත්වාගෙන යමින් සම්ප්‍රේෂනය කිරීමකි. මෙම අවස්ථාව ඉහතදී රූපයකින් දක්වා ඇත.

ඉහත විස්තරය අනුව යමින් දැන් අපට යම් එෆ්එම් සම්ප්‍රේෂනයක් සඳහා අවශ්‍ය කරන මුලු බෑන්ඩ්විත් එක ගණනය කළ හැකියි පහත ආකාරයට.

අවශ්‍ය කරන බෑන්ඩ්විත් එක = 2f_sN (N යනු 0.01ට වඩා වැඩි ජව අනුපාතයක් සහිත සයිඩ්බෑන්ඩ් ගණනයි)

උදාහරණයක් ලෙස, m_f=2 ලෙස පවතින එෆ්එම් සම්ප්‍රේෂකයක උපරිමව සංඥා සංඛ්‍යාතය කිලෝහර්ට්ස් 15 යොදා ගන්නා විට, ඒ සඳහා 2 x 15kHz x 4 = 120kHz ක බෑන්ඩ්විත් එකක් අවශ්‍ය කෙරේ (ඉහත J වගුව බලන විට, mf=2 වන විට සයිඩ්බෑන්ඩ් යුගල 4ක් අවශ්‍ය බව පෙනේ). එම සංඥාවම m_f=0.25 ලෙස පවතින විට, 2 x 15kHz x 1 = 30kHz ක කුඩා බෑන්ඩ්විත් එකක් අවශ්‍ය කෙරේ.

Carson’s rule නම් තවත් ක්‍රමයක් තිබෙනවා සංඛ්‍යාත මූර්ජන සම්ප්‍රේෂනයක් සඳහා අවශ්‍ය කරන බෑන්ඩ්විත් එක සෙවීම සඳහා. එය ඉහත ක්‍රමයටත් වඩා පහසුය. මෙම සූත්‍රයෙහි සංඛ්‍යාත අපගමනය (f_d) තිබෙන නිසා, වක්‍රාකාරයෙන් ඉන් m_f ද, ඉනුත් නැවතත් වක්‍රාකාරයෙන් ඉහත සමීකරණයේ තිබූ N නියෝජනය වේ. ඇත්තටම මෙම සූත්‍රයෙහි පදනම වන්නේ 0.02ට වඩා වැඩි අගයක් සහිත J පද පමණක් සැලකිල්ලට ගැනීමයි. එහෙත් මීට පෙර දුටු සූත්‍රයේදී 0.01ට වඩා වැඩි J පදයි ගත්තේ. ඒ අනුව, කාර්සන්ස් නියමය අනුව ලැබෙන බෑන්ඩ්විත් අගය හැමවිටම ඉහත පළමු ක්‍රමයට ගණනය කර ලැබෙන අගයට වඩා තරමක් අඩුය.

අවශ්‍ය කරන බෑන්ඩ්විත් එක = 2[f_d(max)+f_s(max)]

උදාහරණයක් ලෙස, උපරිම සංඛ්‍යාත අපගමනය කිලෝහර්ට්ස් 5ක් නම් හා උපරිම සංඥා සංඛ්‍යාතය කිලෝහර්ට්ස් 4ක් නම්, අවශ්‍ය කරන බෑන්ඩ්විත් එක 2(5kHz+4kHz) = 18kHz කි.

එෆ්එම් සඳහා සයිඩ්බෑන්ඩ් යුගල කිහිපයක් අවශ්‍ය බව ඉහත සඳහන් විය. එහෙත් කෙනෙකුට ප්‍රශ්නයක් ඇති විය හැකියි වාහකය දෙපස තිබෙන එක් සයිඩ්බෑන්ඩ් යුගලයක් පමණක් ප්‍රමාණවත් නොවන්නේ ඇයිද කියා. ඇත්තටම එය ඇසිය යුතුම ප්‍රශ්නයකි. අපට අවශ්‍ය සංඥාව එහි තිබෙනවානෙ. ඉතිං මොකටද තවත් සයිඩ්බෑන්ඩ් සම්ප්‍රේෂනය කරන්නේ වැඩිපුර විදුලියත් සංඛ්‍යාත පරාසත් “නාස්ති කරමින්” ?

ඔබට හැකිනම්, එෆ්එම් සංඥාවක් ඒඑම් ක්‍රමයෙන් ග්‍රහණය කර බලන්න (එෆ්එම් මූර්ජිත සංඥාවේ වාහකය හා ඒ දෙපස ඇති පළමු සයිඩ්බෑන්ඩ් යුගල හසුකර ගනිමින්). ඔබට එහි ශබ්දය ඇසේවි. ඔව්; ඒ කියන්නේ එෆ්එම් සංඥාවක් ඒඑම් ක්‍රමයෙන් ග්‍රහනය කර ගත හැකියි. එහෙත් එහි ශබ්දය එතරම් කොලිටි නොවේවි. මේ ගැන තවත් විමසා බලමු. (එහෙත් සම්පූර්ණ එෆ්එම් සංඛ්‍යාත පරාසයම ඒඑම් ක්‍රමයෙන් ඇසුවත් කොලිටිය වැඩි නොවේ මක්නිසාද යත් ඒඑම් විමූර්ජකයට බැහැ සයිඩ්බෑන්ඩ් සියල්ලම එකට ගෙන තනි ගුණාත්මය වැඩි අවසාන සංඥාවක් ගොඩනැඟීමට. එය කළ හැක්කේ එෆ්එම් විමූර්ජකයට පමණි.)

එෆ්එම් ක්‍රමය ඒඑම් ක්‍රමයට වඩා වැඩිපුර විදුලියත් සංඛ්‍යාතත් වැය කරනවා නම්, එෆ්එම් ක්‍රමයේ වෙනත් වාසි තිබෙන නිසයි එය බහුලවම භාවිතා කරන්නේ. එහි ප්‍රබලම වාසිය නම්, අවකාශය ඔස්සේ එෆ්එම් රේඩියෝ තරංග පැමිණෙන විට විවිධාකාරයෙන් ඇතිවන ඝෝෂා/අවහිරතාවලට ඉතා හොඳින් ඔරොත්තු දීමේ හැකියාව ඊට තිබීමයි.

රේඩියෝ තරංගයකට අවහිරතා ඇතිවන්නේ තවත් එම සංඛ්‍යාතයම ඇති හෝ ඊට ආසන්න සංඛ්‍යාතයක් ඇති හෝ රේඩියෝ තරංගවලිනි. සමහරවිට මෙම ඝෝෂා/අවහිරතා ඇති කරන රේඩියෝ තරංග අකුණු ගැසීම වැනි ස්වාභාවිකව ඇති වන්නක් විය හැකිය. එහෙමත් නැතිනම්, වාහන එන්ජිමක් ක්‍රියා කිරීම, විදුලි ස්විචයක් ඔන්/ඕෆ් කිරීම වැනි මිනිසා විසින් සෑදූ කෘත්‍රිම උපකරණයකින් අනපේක්ෂිතව ජනිත වූ රේඩියෝ තරංගයක් විය හැකියි. අවහිරතාව ඇති කරන රේඩියෝ තරංගය කුමන ආකාරයකින් ඇති වුවත්, ඉන් අපේ රේඩියෝ තරංගයට ඇති කරන බලපෑම එකමයි. එම අනවශ්‍ය ඝෝෂා තරංගයේ ප්‍රබලතාව වැඩි වන්නට වන්නට අවහිරතාවද ප්‍රබල වේ.

ඒඑම් ක්‍රමයේදී බුද්ධිය/තොරතුරු පවතින්නේ මූර්ජිත සංඥාවේ විස්තාරයේය (එනම්, වාහක තරංගයේ විස්තාරය විචලනය කරමින්නෙ බුද්ධි සංඥාව එහි ගැප් කළේ). ඉතිං, භාහිරින් අපේ සංඥාවේ සංඛ්‍යාත පරාසයේම පවතින වෙනත් ඝෝෂාකාරි රේඩියෝ තරංගයක් ඊට මුසු වූ විට, අනිවාර්යෙන්ම මූර්ජිත සංඥාවේ විස්තාරය වෙනස් වේ. එවිට, රිසීවරයට ලැබෙන්නේ මෙම විස්තාර මට්ටම් විකෘති වූ තරංගයක් වන අතර, රිසීවරයට කිසිදු හෝඩුවාවක් නැහැ සංඥාවට අයිති විස්තාර අගය හා ඝෝෂාවට අයිති විස්තාර අගය වෙන් කර ගන්න. ඉතිං අවසානයේ රිසීවරයෙන් පිටවන්නේ විකෘතියද සහිත බුද්ධි සංඥාවයි.

දැන් ඉහත ආකාරයටම ඝෝෂා රේඩියෝ සංඥාවක් සංඛ්‍යාත මූර්ජිත රේඩියෝ සංඥාව හා මුසු වන්නේ යැයි සිතමු. එවිට පෙර සේම, අපේ මූර්ජිත සංඥාවේ විස්තාර මට්ටම වෙනස් වේ (විකෘති වේ). එහෙත් එය ගැටලුවක් නොවේ මොකද රිසීවරය සැලකිල්ලට ගන්නේ මූර්ජිත සංඥාවේ සංඛ්‍යාතය මිස විස්තාරය නොවේ (එෆ්එම් වලදී සංඥාව ගැප් කළේ සංඛ්‍යාතය මත මිස විස්තාරය මත නොවෙයිනෙ).

ඝෝෂා තරංගවලට බැහැ තවත් සංඥාවක සංඛ්‍යාතයට බලපෑමක් සිදු කරන්නට (සංඥා සංඛ්‍යාතය වෙනස් කරන්නට). මෙම තත්වය උපමාවකින් කියතොත්, අපට නොතේරෙන බසකින් අපට කවුරුන් හෝ බනිනවා වැනිය (කොච්චර බැන්නත් අපට තේරෙන්නේ නැති නිසා අපට කේන්ති යන එකක් නැහැ).

එෆ්එම් මූර්ජිත සංඥාව තුල බුද්ධි තොරතුර සංඛ්‍යාතය මත ගැප් කරනවා යැයි මා ඉහත පැවසුවා. ඇත්තටම එම දේ කිරීමට තමයි වැඩිපුර සයිඩ්බෑන්ඩ් ප්‍රමාණයක් අවශ්‍ය කළේ. අපට ඒ දෙස භාහිරින් බලන විට, වැඩිපුර සයිඩ්බෑන්ඩ් වැයවීම නාස්තියක් මෙන් පෙනුනත්, සංඛ්‍යාත මූර්ජනයේදී පෙර කී ලෙස ඝෝෂාවට අසංවේදීවීමට එලෙස සයිඩ්බෑන්ඩ් රාශියක් තිබීම අත්‍යවශ්‍යය. එය හරියට වැඩිපුර ආරක්ෂාවට අපි සමහර ලියවිලිවල පිටපත් කිහිපයක්ම තබා ගන්නවා වැනි වැඩකි. එක් පිටපතක් සවුත්තු වුවොත්, තවත් හොඳ පිටපතක් එවිට තිබේවි. එලෙසම ඝෝෂාව නිසා යම් සයිඩ්බෑන්ඩ් එකකට බාධාවක් ඇති කළත්, එම තොරතුරම තවත් සයිඩ්බෑන්ඩ් ගණනාවකම තිබෙනවා නේද?

තවද, m_f=0.25 අවස්ථාව (NBFM) ගැනද වචනයක් කිව යුතුය. මෙහි අවශ්‍ය කරන බෑන්ඩ්විත් එක කුඩා නිසා එය කොච්චර හොඳයිද කියා සිතෙනු ඇති. ඔව්, විදුලි බලය හා සංඛ්‍යාතයන් ඉතිරිවීම පැත්තෙන් බලන විට නම්, එය විශාල වාසියකි. එහෙත් මේ සමඟම ගැටලුවක්ද ඇති වේ. එනම්, සයිඩ්බෑන්ඩ් යුගල ගණන අඩු නිසා, ඝෝෂාවට ඔරොත්තු දීමේ හැකියාව ඉතා අඩුය.

එහෙත් අප තබා ගත් සියලු පිටපත් එකවර සවුත්තු වුවොත් නම් කරන්නට දෙයක් නැහැ. අන්න ඒ වගේ, සම්පූර්ණ එෆ්එම් සංඛ්‍යාත පරාසයම ඝෝෂාවට ලක් වුවොත් එෆ්එම් ක්‍රමය වුවද කරදරයට පත් වෙනවා. එහෙත් එලෙස විශාල සංඛ්‍යාත පරාසයක් පුරාවට ප්‍රබල ඝෝෂාවක් අහඹු ක්‍රමවලින් නිතර ඇති වන්නේ නැත. එසේ ඇති වනවා නම්, තවත් සම්ප්‍රේෂකයකින් විසුරුවා හරින රේඩියෝ තරංගයක් විය හැකියි බොහෝවිට. මෙලෙස එකම සංඥා පරාසයේ එෆ්එම් සම්ප්‍රේෂන දෙකක් එකවර සිදු වුවොත්, ඉන් ග්‍රාහකයට ප්‍රබලව සංඥා හසුවන සම්ප්‍රේෂනය පමණි ග්‍රාහකය යොදා ගන්නේ (එවිට දුර්වල සංඥා සහිත අනෙක් චැනලය ඉබේම නොසලකා හැරේ). මෙය එෆ්එම් ක්‍රමයටම සුවිශේෂි තත්වයක් වන අතර, එය capture effect (ග්‍රහන ආචරණය) ලෙස හැඳින්වෙනවා (ඒඑම් ක්‍රමයේදී නම්, එකම සංඛ්‍යාත පරාසයේ චැනල් කිහිපයක් තිබුණොත්, එම චැනල් සියල්ලම එකවර රිසීවරයෙන් ඇසේවි).

තවද, එෆ්එම් සම්ප්‍රේෂකය තුල ඇති මූර්ජකයට වාහක සංඛ්‍යාතයට හෝ සංඥා සංඛ්‍යාත පරාසයට සමාන හෝ ආසන්න ඝෝෂා සංඥාවක් ඇතුලු වුවොත්, එවිටත් ඉන් ඉබේ ගැලවීමට එෆ්එම් ක්‍රමයට බැරිය (මොකද තවම සංඥා එෆ්එම් වී නැත). එවන් ඝෝෂා මූර්ජකයට බැහැ සාමාන්‍ය වාහක හා බුද්ධි සංඥාවෙන් වෙන් කර ගන්නට. ඉතිං එම ඝෝෂාවත් මූර්ජකය විසින් සාමාන්‍ය සංඥාවක් ලෙස භාර ගෙන අවසාන මූර්ජිත සංඥාවට ඇතුලු කරාවි. එනම්, එලෙස ඇතුලු වූ ඝෝෂාව නිසා මූර්ජිත සංඥාවේ සංඛ්‍යාතය විකෘති අගයක් ගනීවි. එවිට එම ඝෝෂාව ආරම්භයේ සිටම පැවති නිසා, අවසානයේ රිසීවරයටද ගමන් කරයි. එය වැලැක්වීම ට්‍රාන්ස්මිටර් පරිපථය තුලට අනවශ්‍ය ඝෝෂා ඇතුලු නොවන ආකාරයට පරිපථ සැලසුම් කළ යුතුය (සුදුසු ෆිල්ටර් පරිපථ අවශ්‍ය තැන්වල යෙදීමෙන් හා වෙනත් උපක්‍රම යොදා). මේ ගැන තවදුරටත් පැහැදිලි කර ගමු.

සිතමු යම් ඝෝෂා තරංගයක් වාහක තරංගයට මූර්ජක පරිපථයට පෙර මිශ්‍ර වෙනවා කියා. එය පහත රූපයේ ආකාරයට phasor diagram එකකින් නිරූපණය කළ හැකියි. එහි C මඟින් සංඛේතවත් කර ඇත්තේ වාහක තරංගයේ ප්‍රබලත්වය වන අතර, N මඟින් සංඛේතවත් කර ඇත්තේ ඝෝෂා තරංගයේ ප්‍රබලත්වයයි (පැහැදිලි කිරීමේ පහසුව තකා ඝෝෂාවේ ප්‍රබලත්වය/විස්තාර අගය නියත යැයි සිතමු; ප්‍රායෝගිකව එම අගය විචලනය වන්නකි).

  

වාහකය හැමවිටම නියත අගයකින් ඒකාකාරව තිබෙන නිසා, එය කාලයත් සමග ස්ථානය වෙනස් නොකර තිබෙන තැන දිගටම රැඳෙනවා. එහෙත් ඝෝෂා තරංගය (විස්තාර අගය නියත යැයි උපකල්පනය කරපු) වාහකයට සාපේක්ෂව ස්ථානය වෙනස් කර ගත හැකියි (එනම්, වාහකයට සාපේක්ෂව කලා කෝණය නිරන්තරයෙන්ම විචලනය විය හැකිය). එය ෆේසර් සටහනේ නිරූපණය කර තිබෙන්නේ කඩඉරි වෘත්තයේ අරය ලෙස N “දණ්ඩ” කරකැවෙන්නා සේය (මෙලෙස ෆේසර් සටහනක වෘත්තයක ආකාරයෙන් විචලනය වන රාශියක් rotating phasor ලෙස හැඳින්වෙන අතර, ඒ අනුව ඝෝෂාව යනු rotating phasor එකක් ලෙසයි අප මේ නිරූපණය කර ඇත්තේ). එවිට N හා C දෙක එක්ව යම් ත්‍රිකෝණයක් නිර්මාණය කරනවා. එම ත්‍රිකෝනයේ කර්ණය (ත්‍රිකෝණයක දිගම රේඛාව) වන S මඟින් දැන් නිරූපණය කෙරෙන්නේ වාහකය හා ඝෝෂාව එක්ව සාදන (සම්ප්‍රයුක්තව) අවසාන තනි සංඥාවයි. මෙම අවසන් තනි සංඥාව දැන් ඝෝෂාව මිශ්‍රිත (එනම් විකෘතිය සහිත) සංඥාවක් බව වටහා ගන්න.

ඉහත ත්‍රිකෝණයේ කර්ණයෙන් නිරූපනය කළ සම්ප්‍රයුක්ත සංඥාව හා වාහකය අතර කලා (කෝණ) වෙනස (phase shift) උපරිම වන්නේ N හා C යන රේඛා ඛණ්ඩ දෙක එකිනෙකට ලම්භකව පිහිටන විටනෙ (එනම් එම ත්‍රිකෝණය ඍජුකෝණී ත්‍රිකෝණයක් බවට පත් වන අවස්ථාව). මෙම අවස්ථාවේදී සම්ප්‍රයුක්ත සංඥාව හා වාහකය අතර කලා කෝණය Φ යැයි සිතමු. එවිට,

sin(Φ) = N/S → Φ = sin^-1(N/S)

තවද, ඉලෙක්ට්‍රොනික්ස් හා විදුලිසංදේශයේදී නිතරම සංඥාව හා ඝෝෂාව අතර වැදගත් සම්බන්දතාවක් භාවිතා කරනවා. එය Signal-to-Noise Ratio (SNR) ලෙස හැඳින්වෙනවා. ඉන් කියන්නේ ඝෝෂාවේ ප්‍රබලත්වයට (වොට් ගණන) සාපේක්ෂව කොච්චරක් සංඥාව ප්‍රබලද යන්නයි. එය සූත්‍රයක් ලෙස පහත ආකාරයටයි දක්වන්නේ.

SNR = (Signal power) / (Noise power) SNR = S/N

උදාහරණයක් ලෙස, යම් සන්නිවේදන පද්ධතියක පවතින සංඥාව වොට් 10ක් නම් හා එහි ඇති සමස්ථ ඝෝෂා සංඥාවේ ප්‍රබලත්වය මිලිවොට් 1ක් නම්, එම පද්ධතියේ SNR අගය වනුයේ, 10,000mW/1mW = 10,000 වේ. එහෙත් SNR අගය සාමාන්‍යයෙන් දක්වන්නේ deciBel (dB) නම් ඒකකයෙනි. 10,000 යන්න ඩෙසිබල් ඒකකයෙන් 40dB වේ (පසු පාඩමකදී ඩෙසිබල් ගැන සොයා බලමු).

ඒ අනුව, ඉහත ලබා ගත් Φ = sin^-1(N/S) යන සූත්‍රයෙහි තිබෙන N/S යනු SNR යන්නෙහි ප්‍රතිලෝමය හෙවත් 1/SNR නේද? ඒ කියන්නේ යම් පද්ධතියක SNR අගය දන්නේ නම්, අපට එහි ප්‍රතිලෝමය සොයා ඉහත සූත්‍රයට දැන් ආදේශක කළ හැකියි.

ඉතිං ඇයි Φ = sin^-1(N/S) සූත්‍රය භාවිතා කරමින් Φ යන කලා කෝණ වෙනස සොයා ගත්තේ? ඊට හේතුව වන්නේ, එම කලා කෝණ වෙනස යොදා ගෙන අපට ඉතාම පහසුවෙන්ම ඝෝෂාව නිසා අවසන් මූර්ජිත සංඥාවේ සිදුවන විකෘතිය (එනම්, ඝෝෂාව නිසා අවසාන මූර්ජිත සංඥාවේ සිදුවන අනවශ්‍ය සංඛ්‍යාත අපගමන ප්‍රමාණය) දැන ගත හැකියි. ඒ සඳහා පහත සූත්‍රය අවශ්‍ය කෙරේ. පහත සූත්‍රයේ කලා කෝණ වෙනස තිබිය යුත්තේ අංශක යන ඒකකයෙන් නොව, රේඩියන් නම් ඒකකයෙනි (අංශක හා රේඩියන් අතර 180⁰ = π^rad යන සම්බන්දතාව ඇති අතර එමඟින් එක් ඒකකයකින් අනෙක් ඒකකයේ විශාලත්වය පහසුවෙන්ම සෙවිය හැකිය).

සංඛ්‍යාත අපගමනය = (කලා කෝණ වෙනස)(සංඥා සංඛ්‍යාතය)        .               δ = Φf_S

උදාහරණයක් ගමු. SNR අගය 3 නම් හා උපරිම සංඥා සංඛ්‍යාතය 1000Hz නම්, ඝෝෂාව නිසා සිදුවන අනවශ්‍ය සංඛ්‍යාත අපගමනය (එනම් සංඛ්‍යාත විකෘතිය) කොපමණද? පළමුව කිව යුත්තේ ඉහත ප්‍රකාශය තුල ඝෝෂාව පවතින බව ඍජුවම නොකිව්වත්, SNR අගයක් දී ඇති නිසා, ඉන් වක්‍රාකාරයෙන් ඝෝෂාව ඇතුලත් කර තිබෙන බවයි. එනම්, ඝෝෂාට වඩා සංඥාව 3 ගුණයක් ප්‍රබලබව ඉන් කියයි.

දැන් SNR හි ප්‍රතිලෝමය 1/3 හෙවත් 0.33 වේ. එම අගය Φ = sin^-1(N/S) යන සූත්‍රයට ඇතුලු කර කලා වෙනස සොයමු. Φ = sin^-1(0.33) = 19.47⁰ වේ. මෙම පිළිතුර ලැබී තිබෙන්නේ අංශක නම් ඒකකයෙන් වන අතර, අපට එය අවශ්‍ය වන්නේ රේඩියන් ඒකකයෙන්ය. එම අගය රේඩියන්වලින් (π/180)x(19.47) = 0.34 වේ. දැන් එම අගය δ = Φf_S සූත්‍රයට යොදන්න. δ = (0.34rad)(1000Hz) = 340Hz වේ. ඒ කියන්නේ මූර්ජනයේදී වාහකයට මුසු වූ ඝෝෂාවක් නිසා හර්ට්ස් 340ක විකෘති සංඛ්‍යාත අපගමනයක් වැඩිපුර සිදු වී ඇත.

එෆ්එම් සංඥාවේ ඝෝෂාවට ඔරොත්තු දීමේ හැකියාව වැඩි කිරීමට හැකියි m_f අගය ඉහල දැමීමෙන් (එවිට සයිඩ්බෑන්ඩ් ප්‍රමාණයද ඉහල යනවා). m_f ඉහල දමනවා යනු, සංඛ්‍යාත අපගමනය (f_d) ඉහල දමනවා යන්නයි. එවිට, ඝෝෂාව නිසා ඉහත පෙන්වා දුන් ආකාරයක විකෘති සංඛ්‍යාත අපගමනයක් සිදු වුවත්, එම විකෘති අපගමනයට වඩා බොහෝ සෙයින් නිල නිවැරදි සංඛ්‍යාත අපගමනය විශාල නිසා, එම විකෘතියේ බලපෑම අඩු වේ. උදාහරණයක් ලෙස, නිල සංඛ්‍යාත අපගමනය කිලෝහර්ට්ස් 34ක් හෙවත් හර්ට්ස් 34000ක් නම්, ඉහත හර්ට්ස් 340ක විකෘති අපගමනය නිවැරදි නිල අපගමනයේ ප්‍රතිශතයක් ලෙස (340/34000)% = 1%කි. එහෙත් නිල අපගමනය කිලෝහර්ට්ස් 68ක් බවට පත් කරන විට, විකෘති අපගමනය දැන් නිල අපගමනයෙන් (340/68000)% = 0.5%කි. ඒ කියන්නේ ප්‍රතිශතයක් ලෙස මුල් අවස්ථාවට වඩා දෙගුණයක් අඩු වී තිබේ (එනම්, විකෘතිය සාපේක්ෂව කුඩා වී තිබේ).

ඝෝෂාව ඉහත විස්තරයේදී මෙන් වාහකයට පමණක් නොවේ සාමාන්‍ය බුද්ධි සංඥාව සමඟද ට්‍රාන්ස්මිටර් පරිපථය තුල මිශ්‍ර විය හැකියි. සාමාන්‍යයෙන් ඝෝෂා සංඥා අධිසංඛ්‍යාත වේ. එනිසා ස්වභාවයෙන්ම එහි වැඩි බලපෑම තිබෙන්නේ වාහක තරංගයටයි මොකද වාහකයද අධිසංඛ්‍යාත තරංගයක් නිසා.

එහෙත්, බුද්ධි සංඥාවේද අවසංඛ්‍යාත තරංග සමඟ අධිසංඛ්‍යාත තරංග තිබිය හැකියි (ඔබ දන්නවා බුද්ධි සංඥාව හැමවිටම වාගේ ෆූරියර් න්‍යායට අනුව අවසංඛ්‍යාත සිට අධිසංඛ්‍යාත දක්වා වූ සංඛ්‍යාත තරංග පරාසයක් සහිතයි). ඒ කියන්නේ බුද්ධි සංඥාවේ අධිසංඛ්‍යාත කොටස්වලට ඝෝෂාවෙන් සිදුවන බලපෑම වැඩියි එහි අවසංඛ්‍යාත කොටස්වලට වඩා. මෙලෙස බුද්ධි සංඥාවේ අධිසංඛ්‍යාත කොටස්වලට අධිසංඛ්‍යාත ඝෝෂාවෙන් සිදුවන බාධාව තවත් වැඩි වෙනවා මොකද බුද්ධි සංඥාවේ අධිසංඛ්‍යාත සංරචක/කොටස් සාමාන්‍යයෙන් දුර්වල (එනම් විස්තාරය අඩු මට්ටමක) පවතින්නේ. එවිට, ඝෝෂාව නිසා ඉතා පහසුවෙන්ම එම අධිසංඛ්‍යාත දුර්වල සංඥා යටපත් වෙනවා. මීට පිළියමක් යෙදිය යුතුමය. නැතහොත් සංඥාවේ අධිසංඛ්‍යාත කොටස් විකෘති වේවි.

මේ සඳහා අපූරු උපක්‍රමයක් යොදනවා එෆ්එම් ට්‍රාන්ස්මිටර් පරිපථවල pre-emphasis යන නමින්. මෙම ප්‍රී-එම්ෆසිස් පරිපථ කොටසින් කරන්නේ සංඥාවේ අධිසංඛ්‍යාත කොටස් පමණක් වර්ධනය කිරීමයි (එනම් බුද්ධි සංඥාවේ සංඛ්‍යාතය ඉහල යන්නට යන්නට ඊට අනුරූපව එම කොටස්වල විස්තාරයන් වැඩිපුර වර්ධනය කරනවා). එවිට අධිසංඛ්‍යාත කොටස්වල ප්‍රබලත්වය ඝෝෂාවේ ප්‍රබලත්වයට වඩා වැඩි වේ. එනම්, SNR අගය වැඩි වේ. එවිට, 1/SNR අගය අඩු වී, විකෘති සංඛ්‍යාත අපගමනයද අඩු වේ. ඒ අනුව, සෑම එෆ්එම් ට්‍රාන්ස්මීටරයකම ප්‍රී-එම්ෆසිස් පරිපථ කොටසක් ඇත.

මෙහි විලෝම ක්‍රියාව හෙවත් de-emphasis ක්‍රියාව එෆ්එම් රිසීවරය තුල සිදු විය යුතුය. එමඟින් ට්‍රාන්ස්මිටරය තුල කෘත්‍රිමව (යම් ප්‍රයෝජනවත් වැඩක් ඉටු කර ගැනීම සඳහා) අප විසින් වැඩි කළ අධිසංඛ්‍යාත කොටස්, රිසීවරය තුල තිබූ මට්ටමට නැවත ප්‍රබලත්වය බැස්සිය යුතුය.